Giáo án powerpoint Bội chung và bội chung nhỏ nhất Toán 6 Cánh diều

1 hộp có 6 1 hộp có quả bóng 8 cái cốc
Vậy chúng ta phải mua ít
nhất bao nhiêu hộp cốc và
bao nhiêu hộp bóng bàn để
số cốc bằng số bóng bàn?
BÀI 13: BỘI CHUNG VÀ BỘI CHUNG NHỎ NHẤT
I. Bội chung và bội chung nhỏ nhất
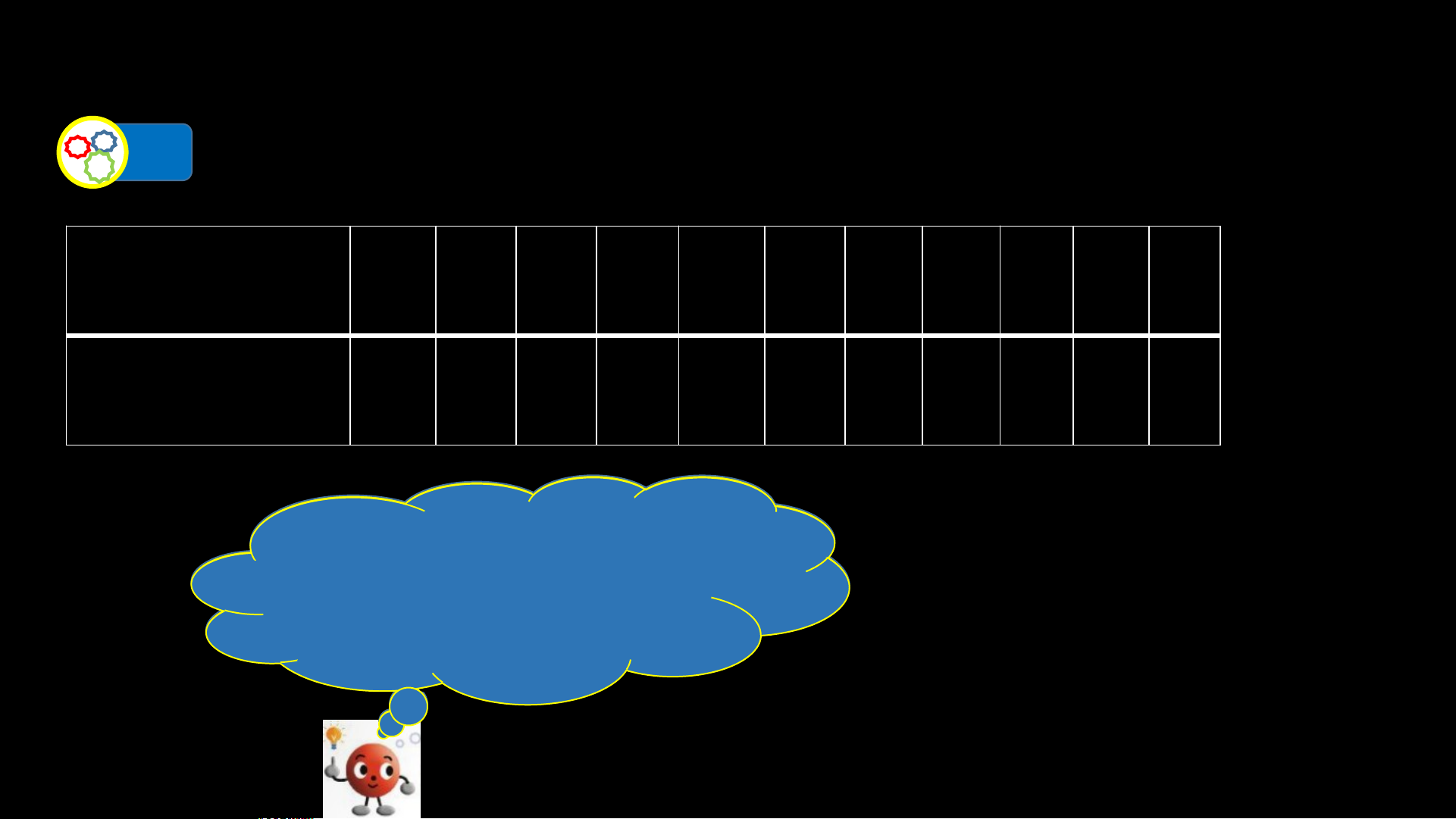
1 a) Nêu một số bội của 2 và 3 theo thứ tự tăng dần: Một số bội 0 2 ? ? ? ? ? ? ? ? 2 của 2 0 ? ? ? ? ? ? ? ? Một số bội 0 3 3 của b) 3
Tìm các số vừa ở trong hàng thứ nhất vừa ở trong hàng 0thứ hai.
c) Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3. Cá Số c nsố hỏ v ừ n a h ở ất t k rhon á g c 0 h tr àn on gg th c ứ ác n b hất ội c v h ừ u a ng ở củtr a on 2 g v h à àn 3 l g à th 6. ứ Số hai đó đ đ ư ư ợc ợc g g ọi ọi llà à b b ội ội cch h u u n n g g c n ủ h a ỏ 2 nhvà ất 3. của 2 và 3.
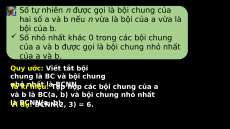
 Số tự nhiên n được gọi là bội chung của
hai số a và b nếu n vừa là bội của a vừa là bội của b.
 Số nhỏ nhất khác 0 trong các bội chung
của a và b được gọi là bội chung nhỏ nhất của a và b.
Quy ước: Viết tắt bội chung là BC và bội chung nhỏ nhất là BCNN.
Ta kí hiệu: Tập hợp các bội chung của a
và b là BC(a, b) và bội chung nhỏ nhất là BCNN(a, b).
Ví dụ: BCNN(2, 3) = 6.