Chuyên đề Đại lượng tỉ lệ nghịch Toán 7 Cánh diều

Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả )
Bài 8. ĐẠI LƯỢNG TỈ LỆ NGHỊCH
A. Kiến thức cần nhớ a y  xy a
1. Định nghĩa: Nếu đại lượng y liên hệ với đại lượng x theo công thức x hay (với a là
hằng số khác 0) thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a.
2. Tính chất: Nếu hai đại lượng tỉ lệ nghịch với nhau thì:
* Tích của một giá trị bất kì của đại lượng này với giá trị tương ứng của đại lượng kia luôn là một
x y x y x y ...   . a hằng số: 1 1 2 2 3 3
* Tỉ số giữa hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của x y x y 1 2 1 3  ;  ,... x y x y đại lượng kia: 2 1 3 1 3. Chú ý:
* Khi đại lượng y tỉ lệ nghịch với đại lượng x thì x cũng tỉ lệ nghịch với y và ta nói hai đại lượng đó tỷ lệ nghịch với nhau.
* Nếu y tỉ lệ nghịch với x theo tỉ lệ a thì x cũng tỉ lệ nghịch với y theo tỉ lệ a. 1
* Nếu y tỉ lệ nghịch với x thì y tỉ lệ thuận với x . a a
* Nếu z tỉ lệ nghịch với y theo tỉ lệ 1 và y tỉ lệ nghịch với x theo tỉ lệ 2 thì z tỉ lệ thuận với x theo a1 a tỉ lệ 2 . B. Một số ví dụ
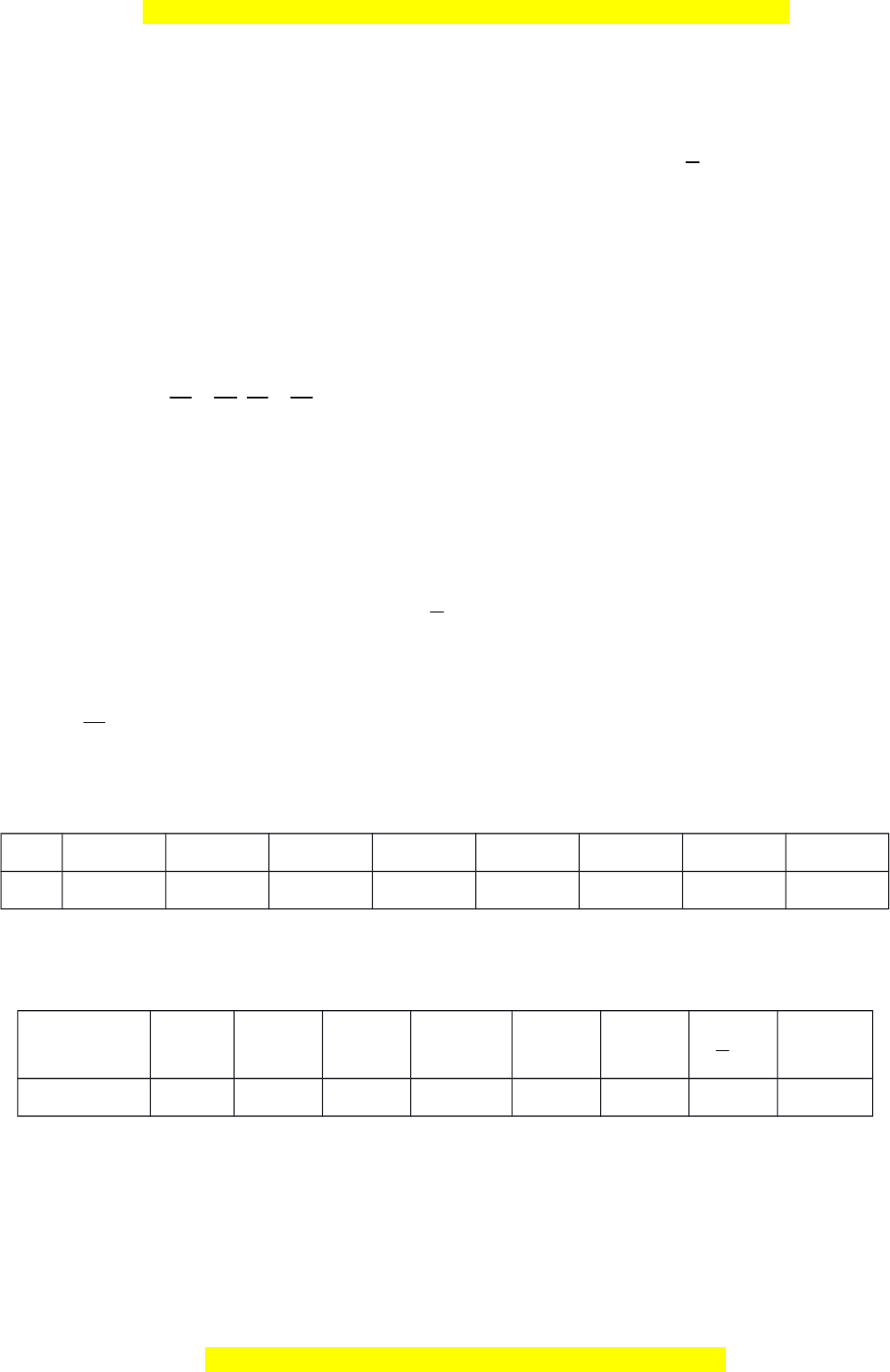
Ví dụ 1: Các giá trị tương ứng của x và y được cho trong hai bảng: x 3 -4,5 5 0,75 22,5 -7,5 y -15 10 -9 -60 -2,5 -8 Bảng I 2 x 3 -0,5 -6 0,95 0,35  5 y 15 -2,5 -30 4,75 -7,5 1975 Bảng II
a) Xác định xem hai đại lượng y và x trong bảng nào tỉ lệ thuận? tỉ lệ nghịch? Tìm các hệ số tỉ lệ
(biết các giá trị tương ứng còn lại cùng có quan hệ tỉ lệ như các giá trị đã cho trong bảng).
b) Điền tiếp các giá trị vào ô trống. M i ọ thắc m c
ắ vui lòng xin liên h h
ệ otline: 084 283 45 85 1
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả )  Tìm cách giải: y kx
- Ta tìm quan hệ tất cả các giá trị tương ứng đã cho của y và x. Nếu có thì y và x tỉ lệ . x y a thuận. Nếu có
thì y tỉ lệ nghịch với x.
- Dựa vào các mối tương quan điền tiếp các số vào ô trống. Giải
3.  15  4,5.10 5
 .  9  0,75.60  45 Tại bảng I: Ta có . . x y  45
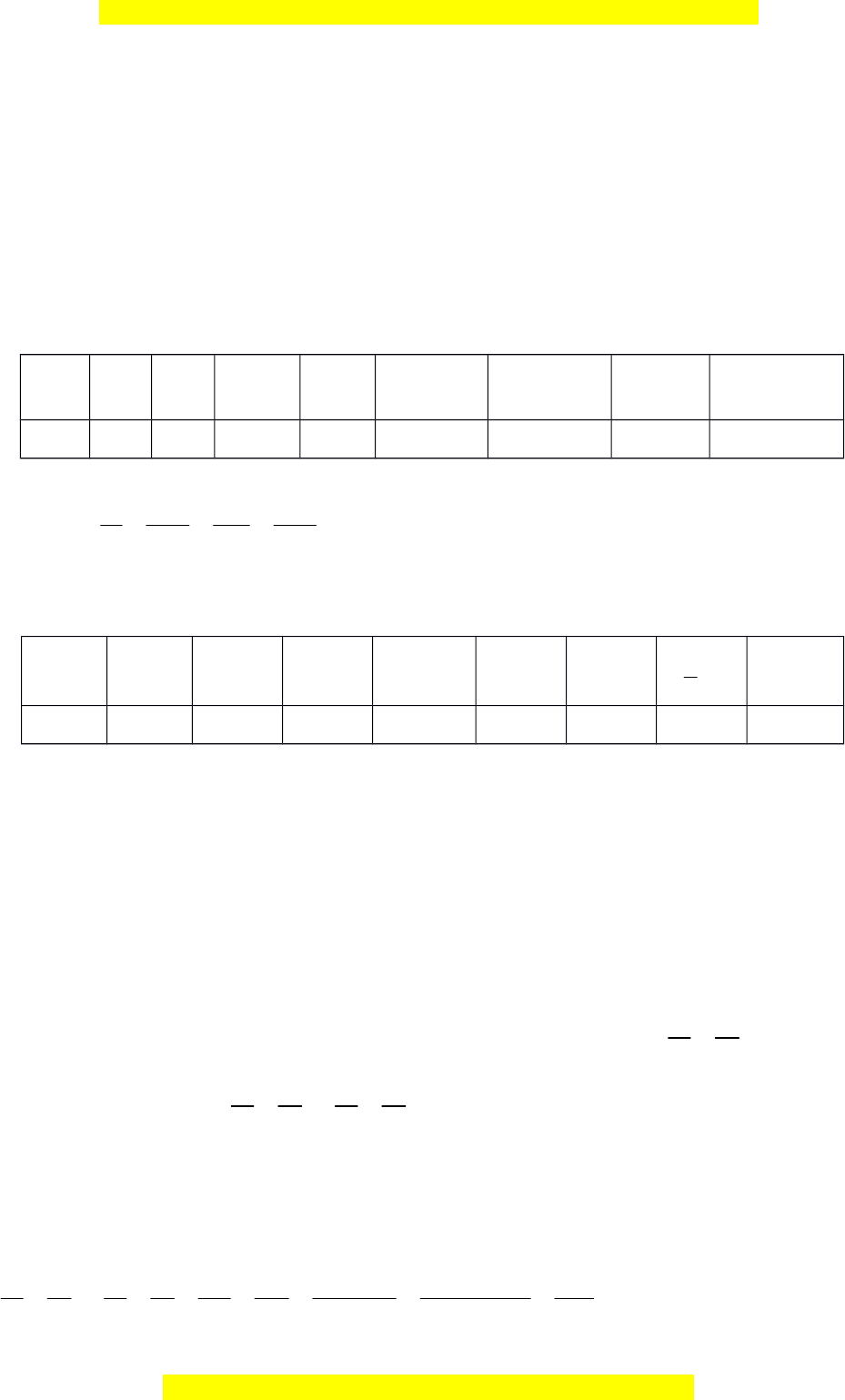
Nên y tỉ lệ nghịch với x. Hệ số tỉ lệ -45. Công thức . 5,62 x 3 - 4,5 5 0,75 18 22,5 -7,5 5 y -15 10 -9 -60 -2,5 -2 6 -8 Bảng I 15  2, 5  30 4,75    5.  Tại bảng II: 3  0,5  6 0,95 y 5  . x
Nên y tỉ lệ thuận với x. Hệ số tỉ lệ 5. Công thức 2 x 3 -0,5 -6 0,95 -1,5 0,35  395 5 y 15 -2,5 -30 4,75 -7,5 1,75 -2 1975 Bảng II x x y y
Ví dụ 2: Cho hai đại lượng tỉ lệ nghịch x và y; 1 và 2 là hai giá trị của x và 1 và 2 là hai giá trị tương ứng của y. y 3  , 5 y 2,5 8x  5x 3  1. Biết 1 ; 2 và 2 1 x , x
Tính 1 2 và hệ số tỉ lệ a của hai đại lượng tỉ lệ nghịch này.
 Tìm cách giải: Ta sử dụng tính chất của đại lượng tỉ lệ nghịch: Tỉ số giữa hai giá trị bất kì của đại x y 1 2  x y
lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia 2 1 , để xuất x y y y 1 2 1 2    8x  5x x y x x hiện 2 1 ta biến đổi 2 1 2
1 và áp dụng tính chất dãy tỉ số bằng nhau. Từ đó x x
tìm 1 và 2 và hệ số tỉ lệ a. Giải
Theo tính chất của đại lượng tỉ lệ nghịch, và áp dụng tính chất dãy tỉ số bằng nhau ta có: x y y y 8y 5y 8y  5y 8.3,5  5.2,5 15,5 1 2 1 2 1 2 1 2         0  ,5. x y x x 8x 5x 8x  5x 31 31 2 1 2 1 2 1 2 1 M i ọ thắc m c
ắ vui lòng xin liên h h
ệ otline: 084 283 45 85 2
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả )
x y : 0,5 2,5 : 0,5 5 Do dó 1 2  x  y : 0,5 3  , 5 : 0, 5 7. Và 2 1 a x .y 5.3  ,5 1  7, 5.
Hệ số tỉ lệ của hai đại lượng là: 1 1
 Chú ý: Ta có thể dùng định nghĩa của đại lượng tỉ lệ nghịch để giải: xy a Từ a a 8a 5a  8 5 
 8y  5y  1 2 x  ; x 
 8x  5x   a  a 1 2 2 1 y y y y  y y   y .y  Ta có 1 2 2 1  2 1   1 2   28 12,5 31 a    y 3  ,5; y 2,5 8x  5x 31   3, 5.2, 5  Thay 1 2 và 2 1  vào ta có:  15,5 31.8, 75 31  . a  a  17  , 5 Hay 8, 75 15,5 17,5 17,5  x  5  ; x  7  . 1 2 3,5 2,5
Ví dụ 3: Năm máy cày cùng loại, mỗi máy làm 8 giờ một ngày thì trong 12 ngày cày xong một cánh đồng.
a) Nếu có 10 máy cày cùng loại trên, mỗi máy làm 8 giờ một ngày thì trong mấy ngày cày xong cánh đồng trên.
b) Cần bao nhiêu máy cày, mỗi máy làm 6 giờ mỗi ngày để 5 ngày cày xong cánh đồng ấy ?
 Tìm cách giải:
a) Cùng một công việc và số giờ làm việc mỗi ngày của mỗi máy, số máy cày và số ngày là hai đại
lượng tỉ lệ nghịch; hoặc cùng một công việc tổng số giờ làm 1 ngày và số ngày hoàn thành công
việc là hai đại lượng tỉ lệ nghịch.
b) Cùng một khối lượng công việc (cày xong cánh đồng) số máy cày và số giờ làm là hai đại lượng
tỉ lệ nghịch. Ta cần tìm số giờ làm của số máy cày trong mỗi trường hợp. Giải  z  0
a) Gọi số ngày cần tìm là z ngày
. Cùng một công việc và số giờ làm việc một ngày của mỗi
máy, số máy cày và số ngày là hai đại lượng tỉ lệ nghịch. 5 z   z 5.  12 :10 6  Ta có: 10 12 (ngày).
* Có thể lý luận cách khác :
Một ngày 5 máy cày với tổng số giờ là 5.8 = 40 (giờ)
Một ngày 10 máy cày với tổng số giờ là 10.8 = 80 (giờ)
Cùng một công việc tổng số giờ làm 1 ngày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch. M i ọ thắc m c
ắ vui lòng xin liên h h
ệ otline: 084 283 45 85 3
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) 40 z   z 40.12 : 80 6  Do đó 80 12 (ngày).
b) Gọi số máy cày cần tìm là t (cái).
Số giờ năm máy cày xong cánh đồng là 8.12 = 96 (giờ).
Số giờ x máy cày xong cánh đồng là 6.5 = 30 (giờ).
Trên cùng một cánh đồng số máy cày và số giờ làm là hai đại lượng tỉ lệ nghịch. Do đó ta có : 96 x   x 96  .5 : 30 1  6. 30 5
Vậy số máy cày cần tìm là 16 cái. a,b,c h ; h ; h Ví dụ 4: Ba cạnh của A
 BC có 4a  6b  5c 220cm . Ba đường cao tương ứng là a b c 3; 4;5 tỉ lệ thuận với
. Tính chu vi của tam giác.
 Tìm cách giải: Cùng diện tích 1 tam giác thì độ dài cạnh và đường cao tương ứng tỉ lệ nghịch
với nhau. Áp dụng tính chất tỉ lệ nghịch và tính chất dãy tỉ số bằng nhau để tìm độ dài các cạnh của tam giác. Giải 2S a  h bh  c  h
Gọi diện tích của A
 BC là S. Ta biết rằng a b
c nên trong một tam giác cạnh và
đường cao tương ứng tỉ lệ nghịch với nhau. 1 1 1 h : h : h 3
a : b : c  : : 2  0 :15 :12.  : 4 : 5 Biết a b c nên 3 4 5 a b c 4a 6b 5c
4a  6b  5c 220        2. Tức là 20 15 12 80 90 60 80  90  60 110 20.2 15.2 12.2 9  4  cm Vậy chu vi tam giác là .
Ví dụ 5: Một ô tô dự định chạy từ A đến B trong một thời gian nhất định. Nếu xe chạy với vận tốc
40km/h thì đến B muộn hơn so với dự định là 30 phút. Nếu xe chạy với vận tốc 60km/h thì đến B
sớm hơn so với dự định là 45 phút. Tính thời gian dự định đi và quãng đường AB.
 Tìm cách giải: Cùng một quãng đường thì vận tốc và thời gian đi tương ứng tỉ lệ nghịch với nhau.
Áp dụng tính chất tỉ lệ nghịch và tính chất dãy tỉ số bằng nhau để tìm độ dài quãng đường và thời gian dự định. Giải
Ta có 45 phút = 0,75 giờ; 30 phút = 0,5 giờ.  t  0
Gọi thời gian dự định là t (giờ);
; Thời gian xe chạy quãng đường AB với vận tốc 40km/h là t  t  0,5 t  t  0,75 1   2  
(giờ). Thời gian xe chạy quãng đường AB với vận tốc 60km/h là . Cùng
một quãng đường thì vận tốc và thời gian đi tương ứng tỉ lệ nghịch với nhau. Do đó theo tính
chất của tương quan tỉ lệ nghịch, ta có: 40 t t t t  t
t  0,5  t  0, 75 1, 25 1 2 1 2 1 2        . 60 t 60 40 60  40 20 20 16 1 M i ọ thắc m c
ắ vui lòng xin liên h h
ệ otline: 084 283 45 85 4