Đề cương ôn tập Cuối kì 1 Toán 10 Chân trời sáng tạo

BỘ SÁCH CHÂN TRỜI SÁNG TẠO
ĐỀ CƯƠNG ÔN TẬP HỌC KÌ I – TOÁN 10 I. Nội dung ôn tập
Chương 1. Mệnh đề và tập hợp Bài 1. Mệnh đề
– Thiết lập và phát biểu được các mệnh đề, bao gồm: mệnh đề phủ định; mệnh đề đảo; mệnh đề
tương đương; mệnh đề có chứa kí hiệu; điều kiện cần, điều kiện đủ, điều kiện cần và đủ.
– Xác định được tính đúng/sai của một mệnh đề trong những trường hợp đơn giản. Bài 2. Tập hợp
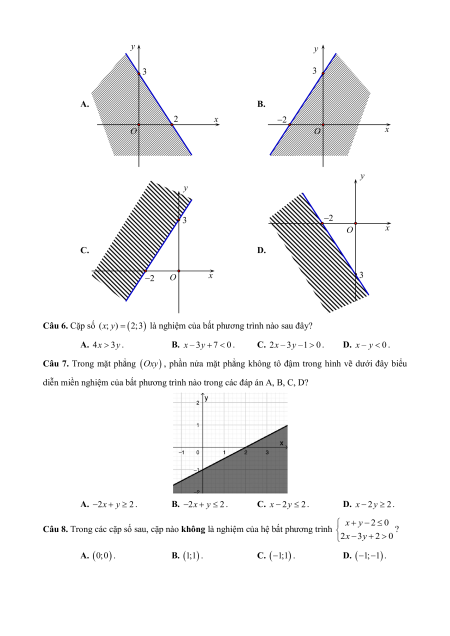
– Nhận biết được các khái niệm cơ bản về tập hợp (tập con, hai tập hợp bằng nhau, tập rỗng) và biết sử dụng các kí hiệu.
Bài 3. Các phép toán trên tập hợp
– Thực hiện được phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù của một tập
con) và biết dùng biểu đồ Ven để biểu diễn chúng trong những trường hợp cụ thể.
– Giải quyết được một số vấn đề thực tiễn gắn với phép toán trên tập hợp (ví dụ: những bài toán liên
quan đến đếm số phần tử của hợp các tập hợp).
Chương 2. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
Bài 1. Bất phương trình bậc nhất hai ẩn
– Nhận biết được bất phương trình bậc nhất hai ẩn.
– Biểu diễn được miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng toạ độ.
Bài 2. Hệ bất phương trình bậc nhất hai ẩn
– Nhận biết được hệ bất phương trình bậc nhất hai ẩn.
– Biểu diễn được miền nghiệm của hệ bất phương trình bậc nhất hai ẩn trên mặt phẳng toạ độ.
– Vận dụng được kiến thức về bất phương trình, hệ bất phương trình bậc nhất hai ẩn vào giải quyết
bài toán thực tiễn (ví dụ: bài toán tìm cực trị của biểu thức F(x; y) = ax + by trên một miền đa giác).
Chương 3. Hàm số bậc hai và đồ thị
Bài 1. Hàm số và đồ thị
– Nhận biết những mô hình dẫn đến khái niệm hàm số.
– Mô tả các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá trị, hàm số đồng
biến, hàm số nghịch biến, đồ thị của hàm số.
– Mô tả dạng đồ thị của hàm số đồng biến, nghịch biến.
– Vận dụng kiến thức của hàm số vào giải quyết một số bài toán thực tiễn. Bài 2. Hàm số bậc hai
– Nhận biết hàm số bậc hai.
– Vẽ parabol (parabola) là đồ thị của hàm số bậc hai.
– Nhận biết các yếu tố cơ bản của đường parabol như đỉnh, trục đối xứng.
– Nhận biết và giải thích các tính chất của hàm số bậc hai thông qua đồ thị.
– Vận dụng kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn.
Chương 4. Hệ thức lượng trong tam giác
Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°
– Nhận biết được giá trị lượng giác của một góc từ 0° đến 180°.
– Tính được giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng máy tính cầm tay.
– Giải thích được hệ thức liên hệ giữa giá trị lượng giác của các góc phụ nhau, bù nhau.
Bài 2. Định lí côsin và định lí sin
– Giải thích được các hệ thức lượng cơ bản trong tam giác: định lí côsin, định lí sin, công thức tính diện tích tam giác.
Bài 3. Giải tam giác và ứng dụng thực tế
– Mô tả được cách giải tam giác và vận dụng được vào việc giải một số bài toán có nội dung thực
tiễn (ví dụ: xác định khoảng cách giữa hai địa điểm khi gặp vật cản, xác định chiều cao của vật khi
không thể đo trực tiếp). Chương 5. Vectơ Bài 1. Khái niệm vectơ
– Nhận biết được khái niệm vectơ, vectơ bằng nhau, vectơ-không.
– Biểu thị được một số đại lượng trong thực tiễn bằng vectơ.
Bài 2. Tổng và hiệu của hai vectơ
– Thực hiện được các phép toán tổng và hiệu hai vectơ.
– Sử dụng được vectơ và các phép toán trên vectơ để giải thích một số hiện tượng có liên quan đến
Vật lí và Hoá học (ví dụ: những vấn đề liên quan đến lực, đến chuyển động).
Bài 3. Tích của một số với một vectơ
– Thực hiện được phép toán tích của một số với vectơ và mô tả được những tính chất hình học (ba
điểm thẳng hàng, trung điểm của đoạn thẳng, trọng tâm của tam giác) bằng vectơ.
– Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán liên quan
đến thực tiễn (ví dụ: xác định lực tác dụng lên vật).
Bài 4. Tích vô hướng của hai vectơ
– Thực hiện được phép toán tích vô hướng của hai vectơ.
– Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán liên quan đến thực tiễn. Chương 6. Thống kê
Bài 1. Số gần đúng và sai số
– Khái niệm số gần đúng, sai số tuyệt đối.
– Xác định số gần đúng của một số với độ chính xác cho trước.
– Xác định sai số tương đối của số gần đúng.
– Xác định số quy tròn của số gần đúng với độ chính xác cho trước.
Bài 2. Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
– Đọc, mô tả được bảng thống kê và biểu đồ.
– Biểu diễn dữ liệu trên các bảng và biểu đồ.
Bài 3. Các số đặc trưng đo xu thế trung tâm của mẫu số liệu
– Tính các số đặc trưng đo xu thế trung tâm của mẫu số liệu: số trung bình, trung vị, tứ phân vị, mốt.
– Biết ý nghĩa, vai trò của các số đặc trưng đo xu thế trung tâm trong mẫu số liệu thực tiễn.
Bài 4. Các số đặc trưng đo độ phân tán của mẫu số liệu
– Tính các số đặc trưng đo độ phân tán.
– Biết ý nghĩa của các số đặc trưng đo độ phân tán.
– Phát hiện các giá trị bất thường sử dụng các công cụ toán học. II. Bài tập tự luyện
A. Trắc nghiệm nhiều phương án lựa chọn
Chương 1. Mệnh đề và tập hợp
Câu 1. Câu nào sau đây không là mệnh đề?
A. Tam giác đều là tam giác có ba cạnh bằng nhau. B. 3 1. C. 4 5 1.
D. Bạn học giỏi quá!
Câu 2. Trong những câu sau, câu nào là mệnh đề chứa biến? A. 18 chia hết cho 9.
B. 3n chia hết cho 9.
C. 2109 là số nguyên tố.
D. Nếu một số chia hết cho 18 thì số ấy chia hết cho 9.
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. 6 2 là số hữu tỷ. B. Phương trình 2
x  7x  2  0 có 2 nghiệm trái dấu. C. 17 là số chẵn. D. Phương trình 2
x  x  7  0 có nghiệm.
Câu 4. Phủ định của mệnh đề: “Hình thoi có hai đường chéo vuông góc với nhau” là:
A. “Hai đường chéo của hình thoi vuông góc với nhau”.
B. “Hình thoi có hai đường chéo không vuông góc với nhau”.
C. “Hình thoi có hai đường chéo bằng nhau”.
D. “Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau”.
Câu 5. Cho các mệnh đề P : “Hình bình hành ABCD có một góc vuông”, Q : “ ABCD là hình chữ
nhật”. Mệnh đề “ P  Q “được phát biểu là
A. Nếu tứ giác ABCD là hình chữ nhật thì ABCD là hình bình hành và có một góc vuông.
B. Nếu hình bình hành ABCD có một góc vuông thì ABCD là hình chữ nhật.
C. Hình bình hành ABCD có một góc vuông khi và chỉ khi ABCD là hình chữ nhật.
D. Hình bình hành ABCD có một góc vuông là điều kiện cần và đủ để ABCD là hình chữ nhật.
Câu 6. Phát biểu mệnh đề đảo của mệnh đề “Nếu 12 chia hết cho 6 thì 12 chia hết cho 3”.
A. Nếu 12 không chia hết cho 6 thì 12 không chia hết cho 3.
B. Nếu 12 chia hết cho 3 thì 12 chia hết cho 6.
C. 12 chia hết cho 6 là điều kiện đủ để 12 chia hết cho 3.
D. 12 chia hết cho 6 khi và chỉ khi 12 chia hết cho 3.
Câu 7. Mệnh đề nào sau đây, có mệnh đề đảo là đúng?
A. Một số tự nhiên có tận cùng bằng 5 thì số đó chia hết cho 5.
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
C. Nếu a và b cùng chia hết cho c thì ab chia hết cho c .
D. Nếu a chia hết cho 2 thì a 1 là số lẻ.
Câu 8. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. “ ABC là tam giác đều  Tam giác ABC cân”.
B. “ ABC là tam giác đều  Tam giác ABC cân và có một góc 60”.
C. “ ABC là tam giác đều  ABC là tam giác có ba cạnh bằng nhau”.
D. “ ABC là tam giác đều  Tam giác ABC có hai góc bằng 60”.
Câu 9. Cho mệnh đề: 2
"x 2x  3x  5  0" . Mệnh đề phủ định sẽ là A. 2 " x
  ,2x  3x 5  0". B. 2 " x
  ,2x  3x 5  0". C. 2 " x
  ,2x  3x 5  0". D. 2 " x
  ,2x  3x 5  0".
Câu 10. Cho mệnh đề P : “Nếu a b  2 thì một trong hai số a và b nhỏ hơn 1”. Mệnh đề nào sau
đây tương đương với mệnh đề đã cho?
A. Điều kiện đủ để một trong hai số a và b nhỏ hơn 1 là a b  2.
B. Điều kiện cần để một trong hai số a và b nhỏ hơn 1 là a b  2.
C. Điều kiện đủ để a b  2 là một trong hai số a và b nhỏ hơn 1. D. Cả B và C.