Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) Bài 3: Phư ng t ơ rình đư ng t ờ h ng ẳ A. Lý thuy t ế I. Phư ng ơ trình tham s c ố a đ ủ ư ng ờ th ng ẳ 1. Vectơ chỉ phư ng ơ c a đ ủ ư ng t ờ h ng ẳ Vectơ u đư c ợ g i ọ là vect ơ chỉ phư ng ơ c a ủ đư ng ờ th ng ẳ ∆ n u ế u ≠ 0 và giá c a ủ u song song ho c ặ trùng v i ớ ∆. Nhận xét: – N u ế u là m t ộ vectơ chỉ phư ng ơ c a
ủ ∆ thì k u (k ≠ 0) cũng là m t ộ vectơ chỉ phư ng c ơ a ủ ∆. – M t ộ đư ng ờ th ng ẳ hoàn toàn đư c ợ xác đ nh ị khi bi t ế m t ộ đi m ể và m t ộ vectơ chỉ phư ng c ơ a ủ đư ng t ờ h ng đó. ẳ Ví d : ụ Đư ng ờ th ng ẳ ∆ đi qua đi m
ể (2 ; 0) và (0 ; –1) có vectơ ch ỉphư ng ơ u nh hì ư nh vẽ sau: 2. Phư ng t ơ rình tham s c ố a đ ủ ư ng t ờ h ng ẳ M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t (c ế ó l i ờ gi i ả ) x x at 0 Hệ y y bt 0
(a2 + b2 > 0 và t là tham s ) ố đư c ợ g i ọ là phư ng ơ trình tham số c a ủ đư ng ờ th ng ẳ ∆ đi qua M u 0(x0 ; y0) và nh n
ậ = (a ; b) làm vectơ chỉ phư ng. ơ x x at 0
Nhận xét: Cho đư ng ờ th ng ẳ ∆ có phư ng ơ trình tham s ố là: y y bt 0 (a2 + b2 > 0 và t là tham s ) ố . + V i ớ m i ỗ giá trị cụ thể c a ủ t, ta xác đ nh ị đư c ợ m t ộ đi m ể trên đư ng ờ th ng ẳ ∆. Ngư c ợ l i ạ , v i ớ m i ỗ đi m ể trên đư ng ờ th ng ẳ ∆, ta xác đ nh ị đư c ợ m t ộ giá trị cụ th c ể a t ủ . + Vectơ u = (a ; b) là m t ộ vectơ ch ph ỉ ư ng c ơ a ∆ ủ . Ví d : ụ a) Vi t ế phư ng ơ trình tham số c a ủ đư ng ờ th ng ẳ ∆ đi qua đi m ể A(1; 2) và có vectơ chỉ phư ng ơ u = (–1 ; 3). x 4 2t b) Cho đư ng ờ th ng ẳ ∆ có phư ng ơ trình tham s ố là y 3 t . Chỉ ra t a ọ độ m t ộ vectơ chỉ phư ng c ơ a ủ ∆ và m t ộ đi m ể thu c đ ộ ư ng t ờ h ng ẳ ∆. Hư ng d ớ ẫn gi i ả a) Phư ng ơ trình đư ng ờ th ng ẳ ∆ đi qua đi m ể A(1; 2) và có vect ơ ch ỉphư ng ơ u x 1 t
= (–1 ; 3) nên có phư ng t ơ rình tham số là y 2 3t . x 1 t V y ậ phư ng t ơ rình tham s c ố a đ ủ ư ng ờ th ng ∆ ẳ là y 2 3t . x 4 2t b) Đư ng t ờ h ng ẳ ∆ có phư ng t ơ
rình tham số là y 3 t . Khi đó ∆ có m t ộ vec t ch ơ ph ỉ ư ng l ơ à (2 ; –1) và đi m ể (4 ; –3) thu c ộ ∆. M i ọ thắc m c
ắ vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) V y ∆ ậ có m t ộ vec t ch ơ ph ỉ ư ng l ơ à (2 ; –1) và đi m ể (4 ; –3) thu c ộ ∆. II. Phư ng t ơ rình t ng quát ổ c a đ ủ ư ng t ờ h ng ẳ 1. Vectơ pháp tuy n c ế a đ ủ ư ng t ờ h ng ẳ Vect ơ n đư c g ợ i ọ là vec t pháp t ơ uy n c ế a ủ đư ng t ờ h ng ẳ ∆ n u ế n ≠ 0 và giá c a vect ủ ơ n vuông góc v i ớ ∆. Nhận xét: – N u ế n là m t ộ vectơ pháp tuy n ế c a
ủ ∆ thì k n (k ≠ 0) cũng là m t ộ vect ơ pháp tuy n c ế a ∆ ủ . – M t ộ đư ng ờ th ng ẳ hoàn toàn đư c ợ xác đ nh ị khi bi t ế m t ộ đi m ể và m t ộ vectơ pháp tuy n c ế a ủ đư ng t ờ h ng đó. ẳ – N u m ế t ộ đư ng ờ th ng ẳ ∆ có vect ch ơ ph ỉ ư ng ơ là u = (a ; b) thì vect ơ n = (–b ; a) là m t ộ vect pháp t ơ uy n c ế a ủ ∆. 2. Phư ng t ơ rình t ng quát ổ c a đ ủ ư ng t ờ h ng ẳ Phư ng
ơ trình ax + by + c = 0 (a và b không đ ng ồ th i ờ b ng ằ 0) đư c ợ g i ọ là phư ng t ơ rình tổng quát c a ủ đư ng t ờ h ng. ẳ Nhận xét: – Đư ng ờ th ng ẳ ∆ đi qua đi m ể M n 0 (x0 ; y0) và nh n
ậ = (a ; b) làm vectơ pháp tuy n có ph ế ư ng t ơ
rình là: a(x – x0) + b(y – y0) = 0 ⇔ ax + by + (–ax0 – by0) = 0. – M i ỗ phư ng
ơ trình ax + by + c = 0 (a và b không đ ng ồ th i ờ b ng ằ 0) đ u ề xác định m t ộ đư ng ờ th ng ẳ ∆ trong m t ặ ph ng ẳ t a ọ đ ộ nh n ậ m t ộ vec t ơ pháp tuy n ế là n = (a ; b). M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t (c ế ó l i ờ gi i ả ) Ví d : ụ Vi t ế phư ng ơ trình t ng ổ quát c a ủ đư ng ờ th ng ẳ d đi qua đi m ể A(1; –2) và có vect pháp t ơ uy n ế n = (–2 ; –3). Hư ng d ớ ẫn gi i ả Theo giả thi t ế , phư ng ơ trình c a ủ đư ng ờ th ng
ẳ d là : –2(x – 1) + (–3).(y + 2) = 0. Từ đó, ta nh n ậ đư c ợ phư ng ơ trình t ng ổ quát c a ủ đư ng ờ th ng ẳ d là –2x – 3y – 4 = 0. V y ậ phư ng t ơ rình t ng quát ổ c a
ủ d là –2x – 3y – 4 = 0.
3. Những dạng đ c bi ặ t ệ c a ph ủ ư ng t ơ rình t ng quá ổ t Cho đư ng ờ th ng ẳ ∆ có phư ng ơ trình t ng
ổ quát ax + by + c = 0 (a ho c ặ b khác 0). a) N u
ế b = 0 và a ≠ 0 thì phư ng ơ trình đư ng ờ th ng
ẳ ∆ trở thành ax + c = 0. Khi đó đư ng ờ th ng ẳ ∆ song song ho c ặ trùng v i ớ tr c ụ Oy và c t ắ tr c ụ Ox t i ạ c ;0 đi m ể a . b) N u
ế b ≠ 0 và a = 0 thì phư ng ơ trình đư ng ờ th ng
ẳ ∆ trở thành by + c = 0. Khi đó đư ng ờ th ng ẳ ∆ song song ho c ặ trùng v i ớ tr c ụ Ox và c t ắ tr c ụ Oy t i ạ c 0; đi m ể b (Hình 30). M i ọ thắc m c
ắ vui lòng xin vui lòng: 084 283 45 85
Lý thuyết Bài 3: Phương trình đường thẳng Toán 10 Cánh diều
412
206 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Bộ câu hỏi lý thuyết Toán lớp 10 mới nhất năm 2023 nhằm giúp Giáo viên có thêm tài liệu tham khảo Lý thuyết môn Toán lớp 10.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(412 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 10
Xem thêmTài liệu bộ mới nhất
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Bài 3: Ph ng trình đ ng th ngươ ườ ẳ
A. Lý thuy tế
I. Ph ng trình tham s c a đ ng th ngươ ố ủ ườ ẳ
1. Vect ch ph ng c a đ ng th ngơ ỉ ươ ủ ườ ẳ
Vect ơ
u
đ c g i là vect ch ph ng c a đ ng th ng ượ ọ ơ ỉ ươ ủ ườ ẳ ∆ n u ế
u
≠
0
và giá
c a ủ
u
song song ho c trùng v i ặ ớ ∆.
Nh n xét: ậ
– N u ế
u
là m t vect ch ph ng c a ∆ thì kộ ơ ỉ ươ ủ
u
(k ≠ 0) cũng là m t vect chộ ơ ỉ
ph ng c a ∆.ươ ủ
– M t đ ng th ng hoàn toàn đ c xác đ nh khi bi t m t đi m và m t vectộ ườ ẳ ượ ị ế ộ ể ộ ơ
ch ph ng c a đ ng th ng đó.ỉ ươ ủ ườ ẳ
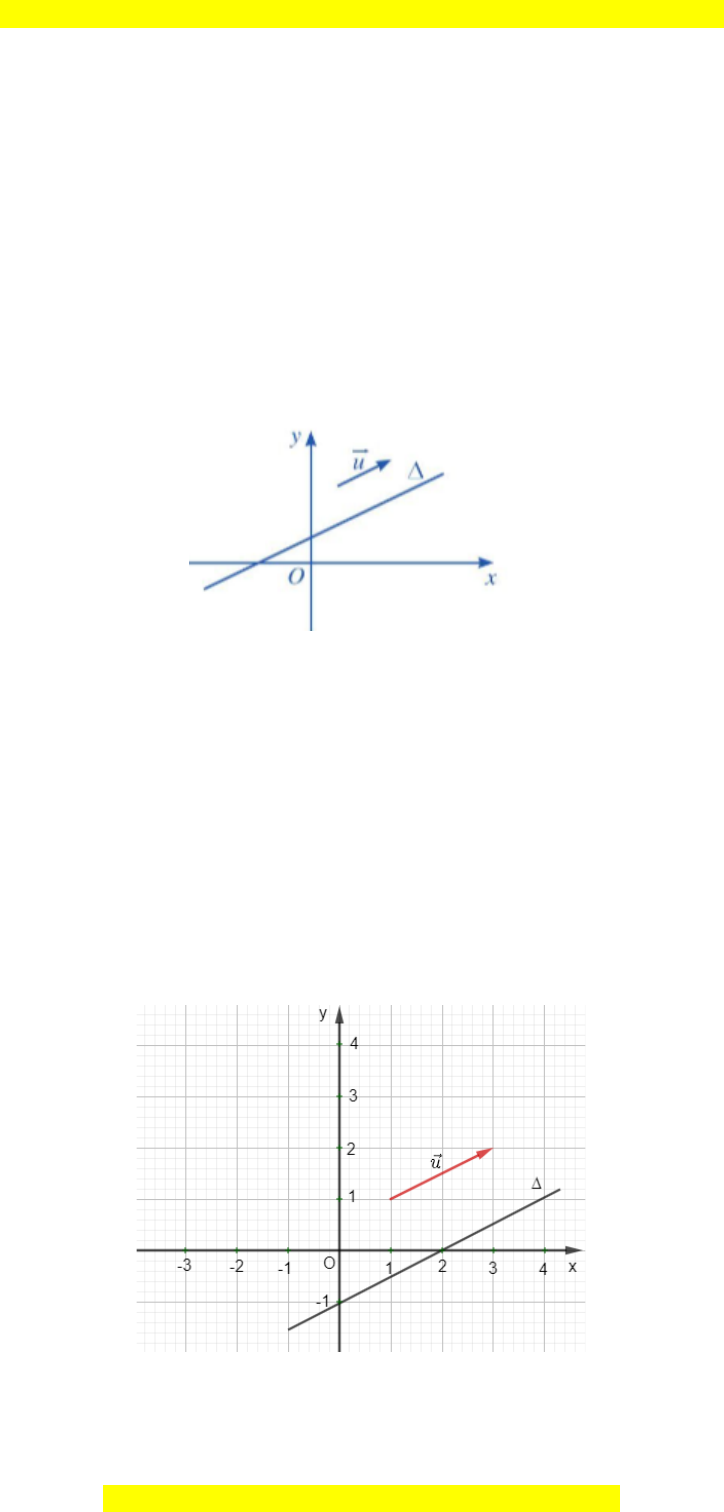
Ví d : ụ Đ ng th ngườ ẳ ∆ đi qua đi m (2 ; 0) và (0 ; –1) có vect ch ph ng ể ơ ỉ ươ
u
nh hình v sau:ư ẽ
2. Ph ng trình tham s c a đ ng th ngươ ố ủ ườ ẳ
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ

Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
H ệ
0
0
x x at
y y bt
(a
2
+ b
2
> 0 và t là tham s ) đ c g i là ph ng trình tham số ượ ọ ươ ố
c a đ ng th ng ∆ đi qua Mủ ườ ẳ
0
(x
0
; y
0)
và nh n ậ
u
= (a ; b) làm vect chơ ỉ
ph ng.ươ
Nh n xét:ậ Cho đ ng th ng ∆ có ph ng trình tham s là: ườ ẳ ươ ố
0
0
x x at
y y bt
(a
2
+
b
2
> 0 và t là tham s ).ố
+ V i m i giá tr c th c a t, ta xác đ nh đ c m t đi m trên đ ng th ngớ ỗ ị ụ ể ủ ị ượ ộ ể ườ ẳ
∆. Ng c l i, v i m i đi m trên đ ng th ng ∆, ta xác đ nh đ c m t giá trượ ạ ớ ỗ ể ườ ẳ ị ượ ộ ị
c th c a t.ụ ể ủ
+ Vect ơ
u
= (a ; b) là m t vect ch ph ng c a ∆.ộ ơ ỉ ươ ủ
Ví d : ụ
a) Vi t ph ng trình tham s c a đ ng th ng ∆ đi qua đi m A(1; 2) và cóế ươ ố ủ ườ ẳ ể
vect ch ph ng ơ ỉ ươ
u
= (–1 ; 3).
b) Cho đ ng th ng ∆ có ph ng trình tham s là ườ ẳ ươ ố
x 4 2t
y 3 t
. Ch ra t a đỉ ọ ộ
m t vect ch ph ng c a ∆ và m t đi m thu c đ ng th ng ∆.ộ ơ ỉ ươ ủ ộ ể ộ ườ ẳ
H ng d n gi iướ ẫ ả
a) Ph ng trình đ ng th ng ∆ đi qua đi m A(1; 2) và có vect ch ph ng ươ ườ ẳ ể ơ ỉ ươ
u
= (–1 ; 3) nên có ph ng trình tham s là ươ ố
x 1 t
y 2 3t
.
V y ph ng trình tham s c a đ ng th ng ∆ là ậ ươ ố ủ ườ ẳ
x 1 t
y 2 3t
.
b) Đ ng th ng ∆ có ph ng trình tham s là ườ ẳ ươ ố
x 4 2t
y 3 t
.
Khi đó ∆ có m t vec t ch ph ng là (2 ; –1) và đi m (4 ; –3) thu c ∆.ộ ơ ỉ ươ ể ộ
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
V y ∆ có m t vec t ch ph ng là (2 ; –1) và đi m (4 ; –3) thu c ∆.ậ ộ ơ ỉ ươ ể ộ
II. Ph ng trình t ng quát c a đ ng th ngươ ổ ủ ườ ẳ
1. Vect pháp tuy n c a đ ng th ngơ ế ủ ườ ẳ
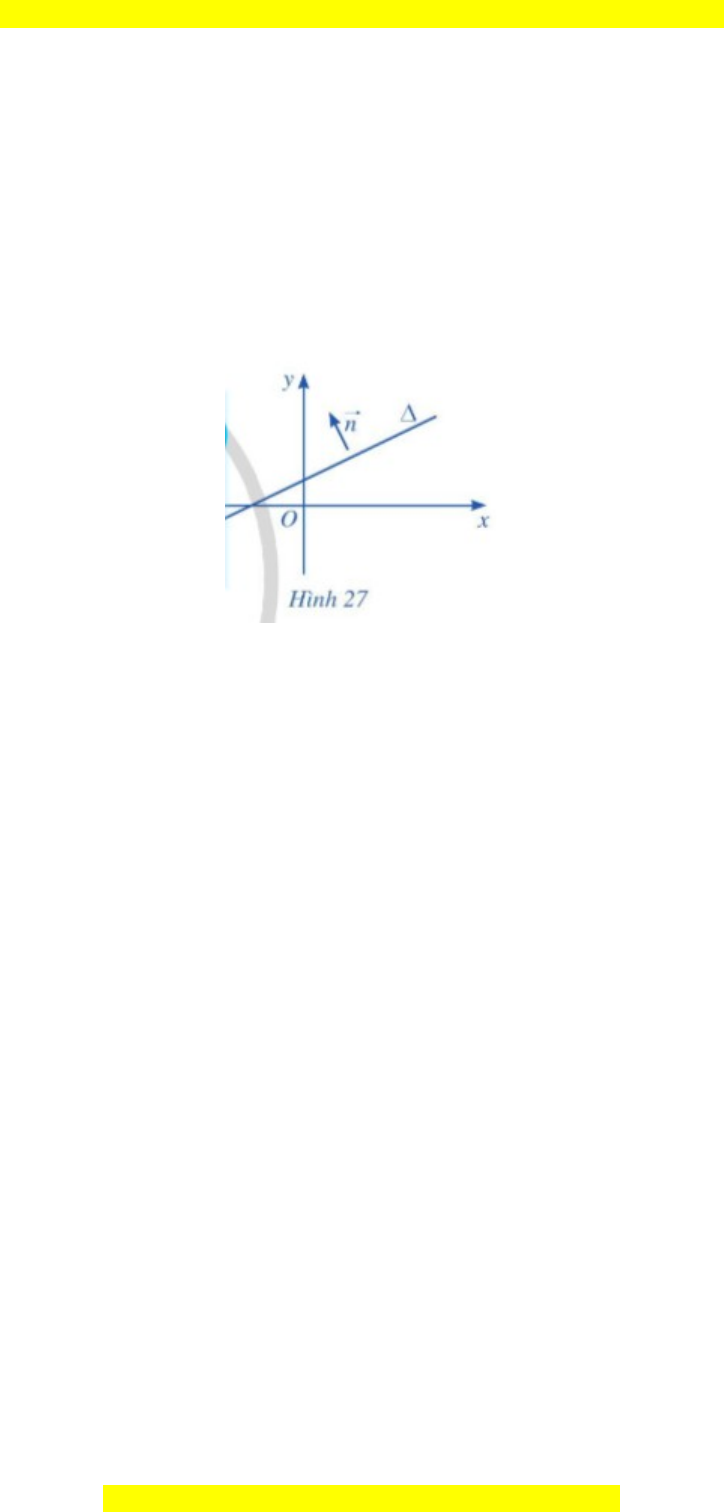
Vect ơ
n
đ c g i là vec t pháp tuy n c a đ ng th ng ∆ n u ượ ọ ơ ế ủ ườ ẳ ế
n
≠
0
và giá
c a vect ủ ơ
n
vuông góc v i ∆.ớ
Nh n xét: ậ
– N u ế
n
là m t vect pháp tuy n c a ∆ thì kộ ơ ế ủ
n
(k ≠ 0) cũng là m t vect phápộ ơ
tuy n c a ∆.ế ủ
– M t đ ng th ng hoàn toàn đ c xác đ nh khi bi t m t đi m và m t vectộ ườ ẳ ượ ị ế ộ ể ộ ơ
pháp tuy n c a đ ng th ng đó.ế ủ ườ ẳ
– N u m t đ ng th ng ∆ có vect ch ph ng là ế ộ ườ ẳ ơ ỉ ươ
u
= (a ; b) thì vect ơ
n
= (–b
; a) là m t vect pháp tuy n c a ∆.ộ ơ ế ủ
2. Ph ng trình t ng quát c a đ ng th ngươ ổ ủ ườ ẳ
Ph ng trình ax + by + c = 0 (a và b không đ ng th i b ng 0) đ c g i làươ ồ ờ ằ ượ ọ
ph ng trình t ng quát c a đ ng th ng.ươ ổ ủ ườ ẳ
Nh n xét: ậ
– Đ ng th ng ∆ đi qua đi m Mườ ẳ ể
0
(x
0
; y
0
) và nh n ậ
n
= (a ; b) làm vect phápơ
tuy n có ph ng trình là: a(x – xế ươ
0
) + b(y – y
0
) = 0 ⇔ ax + by + (–ax
0
– by
0
) = 0.
– M i ph ng trình ax + by + c = 0 (a và b không đ ng th i b ng 0) đ u xácỗ ươ ồ ờ ằ ề
đ nh m t đ ng th ng ∆ trong m t ph ng t a đ nh n m t vec t pháp tuy nị ộ ườ ẳ ặ ẳ ọ ộ ậ ộ ơ ế
là
n
= (a ; b).
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Ví d : ụ Vi t ph ng trình t ng quát c a đ ng th ng d đi qua đi m A(1; –2)ế ươ ổ ủ ườ ẳ ể
và có vect pháp tuy n ơ ế
n
= (–2 ; –3).
H ng d n gi iướ ẫ ả
Theo gi thi t, ph ng trình c a đ ng th ng d là : –2(x – 1) + (–3).(y + 2) =ả ế ươ ủ ườ ẳ
0.
T đó, ta nh n đ c ph ng trình t ng quát c a đ ng th ng d là –2x – 3y –ừ ậ ượ ươ ổ ủ ườ ẳ
4 = 0.
V y ph ng trình t ng quát c a d là –2x – 3y – 4 = 0.ậ ươ ổ ủ
3. Nh ng d ng đ c bi t c a ph ng trình t ng quátữ ạ ặ ệ ủ ươ ổ
Cho đ ng th ngườ ẳ ∆ có ph ng trình t ng quát ax + by + c = 0 (a ho c b khácươ ổ ặ
0).
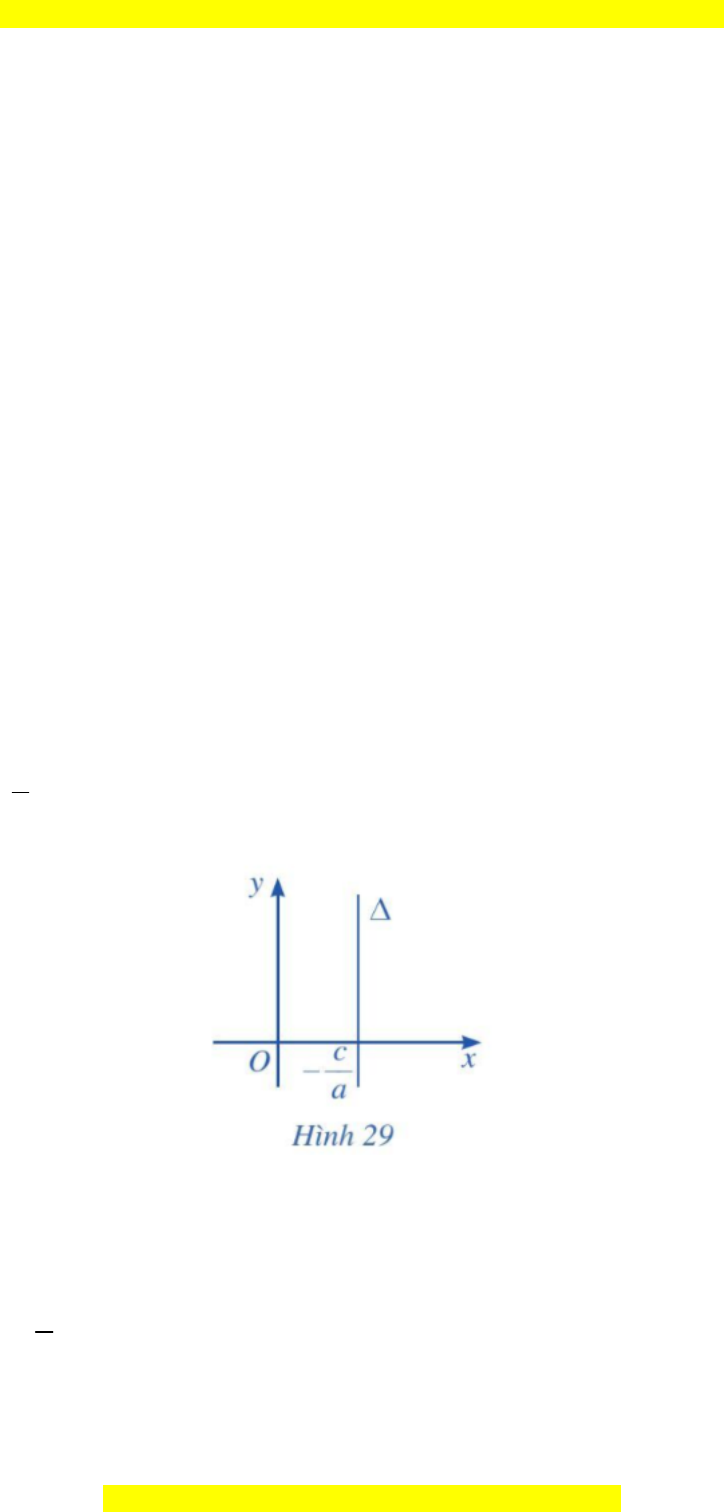
a) N uế b = 0 và a ≠ 0 thì ph ng trình đ ng th ng ∆ tr thành ax + c = 0.ươ ườ ẳ ở
Khi đó đ ng th ng ∆ song song ho c trùng v i tr c Oy và c t tr c Ox t iườ ẳ ặ ớ ụ ắ ụ ạ
đi m ể
c
;0
a
.
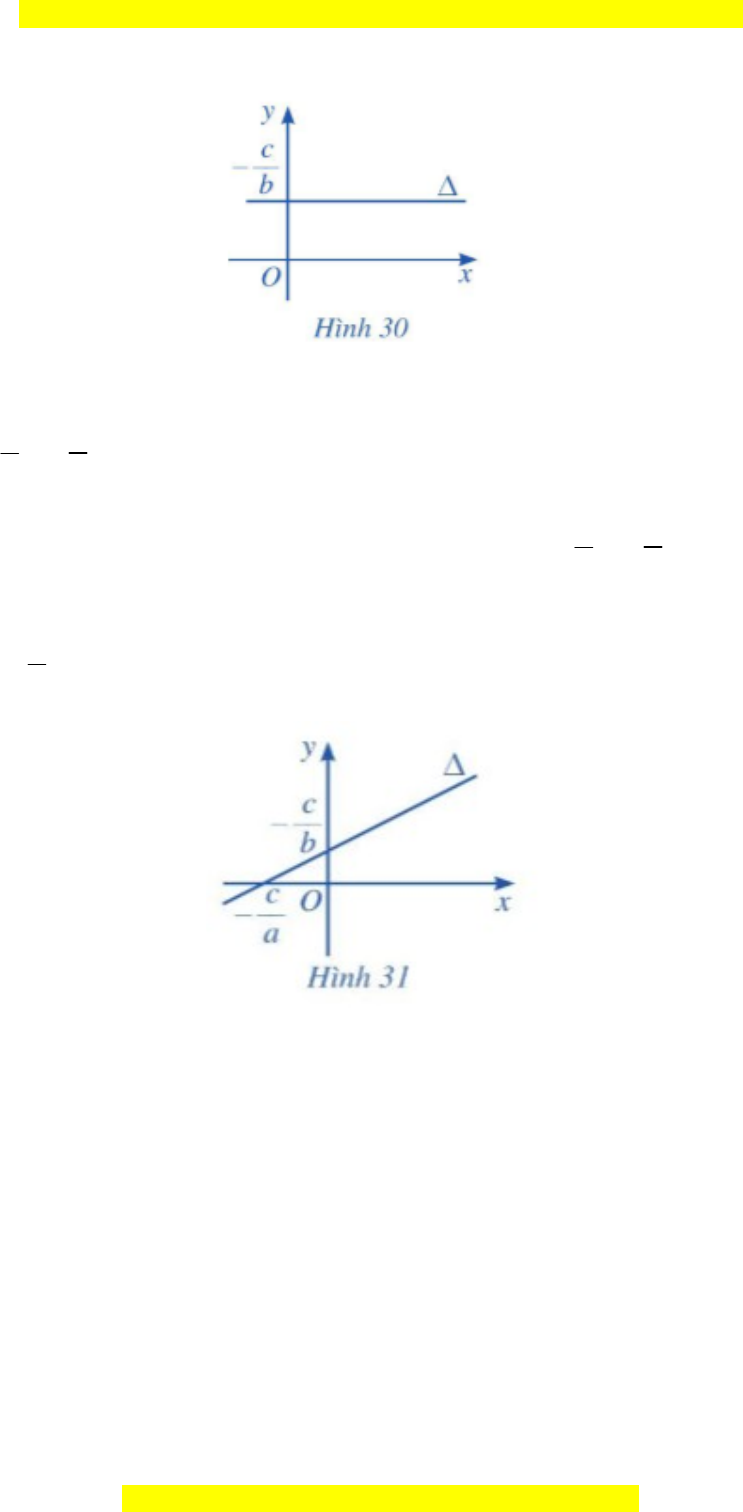
b) N u b ế ≠ 0 và a = 0 thì ph ng trình đ ng th ngươ ườ ẳ ∆ tr thành by + c = 0.ở
Khi đó đ ng th ng ∆ song song ho c trùng v i tr c Ox và c t tr c Oy t iườ ẳ ặ ớ ụ ắ ụ ạ
đi m ể
c
0;
b
(Hình 30).
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
c) N u b ế ≠ 0 và a ≠ 0 thì ph ng trình đ ng th ng ∆ có th vi t thànhươ ườ ẳ ể ế
y =
a
b
x –
c
b
.
Khi đó, đ ng th ng ∆ là đ th hàm s b c nh t y = ườ ẳ ồ ị ố ậ ấ
a
b
x –
c
b
v i h s gócớ ệ ố
là k =
a
b
(Hình 31).
Nh n xét: ậ
– Đ ng th ng ∆ có ph ng trình t ng quát ax + by + c = 0 (a ho c b khác 0)ườ ẳ ươ ổ ặ
là đ th c a hàm s b c nh t khi và ch khi a ồ ị ủ ố ậ ấ ỉ ≠ 0 và b ≠ 0.
– Ph ng trình tr c hoành là y = 0, ph ng trình tr c tung là x = 0.ươ ụ ươ ụ
Ví d : ụ
a) Cho ph ng trình đ ng th ng ∆ là 2x + 4 = 0. Khi đó đ ng th ng ∆ songươ ườ ẳ ườ ẳ
song v i tr c Oy và c t tr c Ox t i đi m (–2 ; 0) ớ ụ ắ ụ ạ ể
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ