CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN
Dạng 1: Biết đồ thị hoặc BBT của hàm số BÀ , xé I t c TO ác ÁN bài X toá ÉT S n l Ự iên TƯ q Ơua N n G đế GIn p A h O ương trình có dạng , .
CỦA ĐỒ THỊ CÁC HÀM SỐ
Dạng 2: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng , .
Dạng 3: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng , .
Dạng 4: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng .
Dạng 5: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng .
Dạng 6: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng .
Dạng 7: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình,
bất phương trình chứa .
Dạng 8: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng .
Dạng 9: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến phương trình có dạng
Dạng 10: Biết số nghiệm của phương trình
, xét các bài toán liên quan đến phương trình có chứa .
Dạng 11: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến BẤT
PHƯƠNG TRÌNH có dạng
có thể có tham số.
Dạng 12: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến BẤT
PHƯƠNG TRÌNH có dạng
có thể có tham số.
CÁC DẠNG TOÁN VỀ HÀM ẨN LIÊN QUAN ĐẾN BÀI TOÁN
XÉT SỰ TƯƠNG GIAO CỦA ĐỒ THỊ CÁC HÀM SỐ (PHẦN 1. Từ dạng 1 đến dạng 4)
Dạng 1: Biết đồ thị hoặc BBT của hàm số
, xét các bài toán liên quan đến
phương trình có dạng , . Câu 1. Cho hàm số
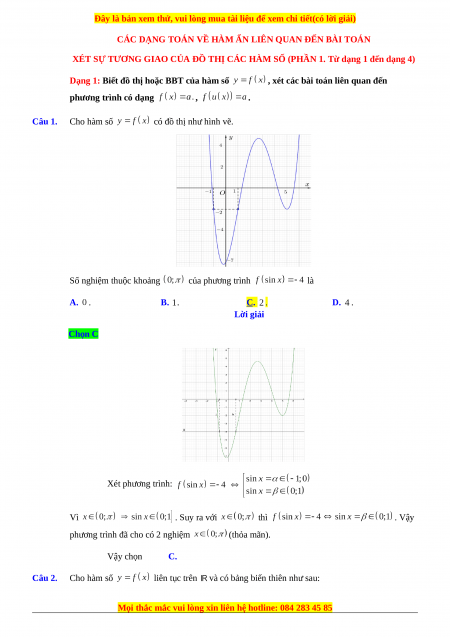
có đồ thị như hình vẽ.
Số nghiệm thuộc khoảng của phương trình là A. . B. . C. . D. . Lời giải Chọn C Xét phương trình: Vì . Suy ra với thì . Vậy
phương trình đã cho có 2 nghiệm (thỏa mãn). Vậy chọn C. Câu 2. Cho hàm số
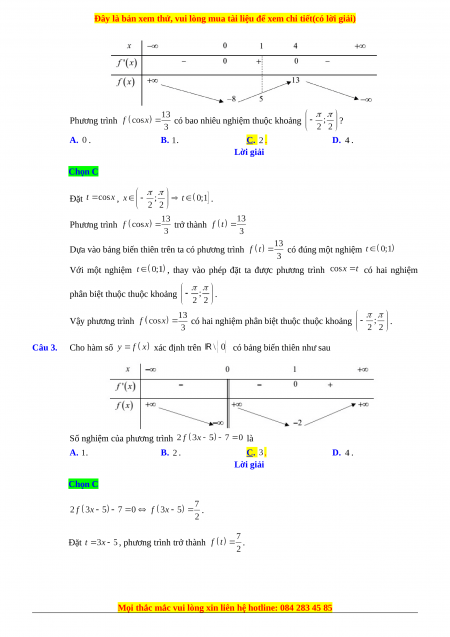
liên tục trên và có bảng biến thiên như sau:
Phương trình
có bao nhiêu nghiệm thuộc khoảng ? A. . B. . C. . D. . Lời giải Chọn C Đặt , . Phương trình trở thành
Dựa vào bảng biến thiên trên ta có phương trình có đúng một nghiệm Với một nghiệm
, thay vào phép đặt ta được phương trình có hai nghiệm
phân biệt thuộc thuộc khoảng . Vậy phương trình
có hai nghiệm phân biệt thuộc thuộc khoảng . Câu 3. Cho hàm số xác định trên
có bảng biến thiên như sau
Số nghiệm của phương trình là A. . B. . C. . D. . Lời giải Chọn C . Đặt
, phương trình trở thành .
Với mỗi nghiệm thì có một nghiệm
nên số nghiệm của phương trình
bằng số nghiệm của phương trình .
Dựa vào bảng biến thiên của hàm số suy ra phương trình có nghiệm
phân biệt nên phương trình có nghiệm phân biệt. Câu 4. Cho hàm số
liên tục trên thỏa mãn điều kiện và có
đồ thị như hình dưới đây
Với giả thiết, phương trình
có nghiệm. Giả sử khi tham số thay đổi, phương trình đã
cho có nhiều nhất nghiệm và có ít nhất nghiệm. Giá trị của bằng A. . B. . C. . D. . Lời giải Chọn C
Dễ thấy điều kiện của phương trình đã cho là . Đặt . Dễ thấy phương trình luôn có nghiệm duy nhất .
Phương trình đã cho có dạng: .
Số nghiệm của phương trình đã cho bằng số nghiệm của (2). Đồ thị hàm số có dạng:
Document Outline
- A. 0. B. 1. C. 2. D. 3
- Câu 8. Cho hàm số có đồ thị như hình vẽ bên.
- Tất cả các giá trị của m để phương trìnhcó hai nghiệm phân biệt là
- Lời giải
- Chọn C