Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả )
CHƯƠNG VII. BÀI 6. TRƯ N Ờ G H P Ợ B N Ằ G NHAU TH BA Ứ C A Ủ TAM GIÁC GÓC – C N Ạ H – GÓC I. CÁC KI N Ế TH C Ứ C N Ầ NHỚ 1. Trư n ờ g h p ợ b n ằ g nhau th b ứ a c a ủ tam giác
Nếu một cạnh và hai góc kề c a
ủ tam giác này bằng một cạnh và hai góc k c ề a ủ tam giác kia thì
hai tam giác đó bằng nhau. B B BC B C C C Ví d 1: ụ
Cho hai tam giác ABC và A B C có: A BC A B C (g – c – g). 2. Trư n ờ g h p ợ b n ằ g nhau c n ạ h huy n ề – góc nh n ọ c a h ủ ai tam giác vuông
Nếu cạnh huyền và một góc nh n ọ c a
ủ tam giác vuông này bằng cạnh huy n và ề m t ộ góc nh n ọ c a
ủ tam giác vuông kia thì hai tam giác vuông đó b ng nha ằ u. Ví d 1: ụ
Cho hai tam giác ABC và A B C có: A A 90 BC B C B B A BC A B C (cạnh huy n – góc ề nh n). ọ
3. Các dạng toán thư n ờ g g p ặ Dạng 1. Ch n
ứ g minh hai tam giác b n ằ g nhau theo trư n ờ g h p ợ góc – c n ạ h – góc. Phư n ơ g pháp: S d ử ng t ụ rư ng ờ h p b ợ
ằng nhau góc – cạnh – góc của tam giác và trư ng ờ h p b ợ ằng nhau cạnh huyền – góc nh n c ọ a ủ tam giác vuông. Dạng 2. Ch n ứ g minh hai đo n ạ th n ẳ g b n ằ g nhau. Tính đ d ộ ài đo n ạ th n ẳ g. Phư n ơ g pháp: + Ch n ọ hai tam giác ch a ứ các đo n t ạ h ng c ẳ n t ầ ính. M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) + Ch ng
ứ minh hai tam giác b ng nha ằ u theo trư ng ờ h p góc ợ c nh góc ạ . + Suy ra các y u t ế ố cần thi t ế đ gi ể ải bài toán.
Dạng 3. Bài toán s d ử n ụ g nhi u ề trư n ờ g h p ợ b n ằ g nhau c a tam gi ủ ác. Phư n ơ g pháp: S d ử ng c ụ ác trư ng ờ h p b ợ ằng nhau đã h c
ọ của tam giác: cạnh – cạnh – cạnh, cạnh – góc –
cạnh, góc – cạnh – góc ... và các trư ng ờ h p b ợ ằng nhau c a ủ tam giác vuông. II. PH N Ầ TR C Ắ NGHI M Ệ Câu 1.
Cho tam giác ABC và tam giác NPM có BC PM ;
B P . Cần thêm m t ộ đi u ề ki n ệ gì để
tam giác MPN và tam giác CBA bằng nhau theo trư ng h ờ p góc ợ – cạnh – góc? A. M A . B. A P . C. C M . D. A N . Câu 2.
Cho tam giác ABC và tam giác DEF có BC EF ;
B F . Cần thêm m t ộ đi u ề ki n ệ gì để
tam giác ABC và tam giác DFE bằng nhau theo trư ng h ờ p góc ợ – cạnh – góc? A. A E . B. A D . C. C E . D. C D . Câu 3.
Cho tam giác ABC và tam giác MNP có A M ;
B N . Cần thêm đi u ề ki n ệ gì đ t ể am giác
ABC và tam giác MNP bằng nhau theo trư ng h ờ p góc ợ – cạnh – góc? A. AC M P .
B. AB MN .
C. BC NP . D. AC M N . Câu 4.
Cho tam giác IKQ và tam giác MNP có I M ;
K P . Cần thêm đi u ề ki n ệ gì đ ể tam giác
IKQ và tam giác MNP bằng nhau theo trư ng h ờ p góc ợ – cạnh – góc?
A. IQ MN .
B. IK MP .
C. QK NP . D. IK M N . Câu 5.
Cho tam giác PQR và tam giác DEF có P D 6
0 , PR DE, R E . Phát bi u ể nào trong các phát bi u s ể au đây là đúng:
A. PQR DEF
B. PQR DEF .
C. RQP F
DE . D. PQR D FE . Câu 6. Cho góc nh n
ọ xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox k đ ẻ ư ng t ờ hẳng song song v i
ớ Oy cắt Oz tại M . Qua M kẻ đư ng ờ th ng ẳ song song v i
ớ Ox cắt Oy ở B . Ch n ọ câu đúng.
A. OA O ; B MA MB B. OA O ; B MA M B
C. OA OB; MA MB
D. OA O ; B MA M B . Câu 7. Cho góc nh n
ọ xOy, Oz Oz E là tia phân giác c a ủ góc đó. Trên lấy đi m ể , vẽ đư ng ờ th ng ẳ qua E vuông góc v i
ớ Ox tại K , cắt Oy tại N . Vẽ đư ng ờ th ng
ẳ qua E vuông góc v i ớ Oy
tại H cắt Ox tại M . Ch n ọ câu đúng.
A. OK OH; KN HM B. OK O
H ; KN HM
C. OK OH; KN HM D. OK O
H ; KN HM . M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả )
Câu 8. Cho đoạn th ng
ẳ AB, O là trung đi m ể c a
ủ AB . Trên cùng m t ộ n a ử m t ặ ph ng ẳ bờ AB vẽ các tia A ; x By vuông góc v i ớ AB . G i ọ C là đi m ể thu c ộ tia Ax . Đư ng ờ vuông góc v i ớ OC tại
O cắt tia By tại D . Khi đó A. BD CD AC . B. AC CD BD .
C. CD AC BD
D. CD AC BD .
Câu 9. Cho tam giác ABC có AB AC . Trên các cạnh AB và AC lấy các điểm D, E sao cho AD AE . G i
ọ K là giao điểm của BE và CD . Ch n c ọ âu sai. A. BE C D . B. BK C K . C. BD C E .
D. DK KC .
Câu 10. Cho tam giác ABC có AB AC . Tia phân giác c a
ủ góc A cắt BC Ở K . Từ B kẻ đư ng ờ vuông góc v i
ớ AK tại H cắt AC ở D . Ch n ọ câu sai.
A. HB HD .
B. HB AD .
C. AB AD . D. ABH ADH .
Câu 11. Cho tam giác DEF và tam giác HKG có D H; E K; DE HK . Bi t ế F 8 0 . Số đo góc G là: A. 70 . B. 80 . C. 90 . D. 100 .
Câu 12. Cho tam giác DEF và tam giác HKG có D K , E G
, DE KG . Bi t ế F 7 5 . Số đo góc H là: A. 70 . B. 75 . C. 90 . D. 100
Câu 13. Cho tam giác ABC và tam giác DEF có AB DE, B E, A D . Bi t ế AC 6 cm . Độ dài DF là: A. 4cm . B. 5cm . C. 6cm . D. 7cm .
Câu 14. Cho ABC và D
EF có AB DE, B E, A D . Biết AC 6 cm . Đ dà ộ i DF là A. 4 cm . B. 5 cm . C. 6 cm . D. 7 cm .
Câu 15. Cho ABC vuông tại A có AB AC . Qua A xy B C kẻ đư ng ờ th ng ẳ sao cho , nằm cùng phía v i ớ xy . K
ẻ BD, CE vuông góc v i ớ xy . Ch n ọ câu đúng?
A. DE BD CE .
B. DE BD CE .
C. CE BD DE .
D. CE BD DE .
Câu 16. Cho ABC có D là trung đi m ể c a
ủ AB . Qua D kẻ đư ng ờ thẳng song song v i ớ BC , cắt
AC tại E , đư ng
ờ thẳng qua E và song song v i
ớ AB , cắt BC tại F . Khi đó
A. ADE EFC . B. A
DE DBF .
C. EFC DBF .
D. Cả ba đáp án đều đúng.
Câu 17. Cho ABC có A 60
. Tia phân giác góc B cắt của AC tại đi m
ể D . Tia phân giác góc C cắt c a ủ AB IE 2 cm
tại điểm E . Các tia phân giác đó cắt nhau tại I . Tính độ dài ID , biết . A. ID 4 cm . B. ID 2 cm . C. ID 8 cm . D. ID 3 cm . M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả )
Câu 18. Hai đoạn thẳng AB, CD song song v i ớ nhau. Hai đo n t ạ h ng nà ẳ y chắn gi a ữ hai đư ng ờ th ng ẳ
song song AC, BD . Ch n ọ câu đúng. A. ID 4 cm . B. ID 2 cm . C. ID 8 cm . D. ID 3 cm . M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Chuyên đề Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc Toán 7 Cánh diều
809
405 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Bài tập Chuyên đề Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc Toán lớp 7 Cánh diều được biên soạn theo các mức độ, có lời giải nhằm giúp Giáo viên có thêm tài liệu tham khảo.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(809 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 7
Xem thêmTài liệu bộ mới nhất
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
CH NG VII. BÀI 6. TR NG H P B NG NHAU TH BA C A TAM GIÁC ƯƠ ƯỜ Ợ Ằ Ứ Ủ
GÓC – C NH – GÓCẠ
I. CÁC KI N TH C C N NHẾ Ứ Ầ Ớ
1. Tr ng h p b ng nhau th ba c a tam giácườ ợ ằ ứ ủ
N u m t c nh và hai góc k c a tam giác này b ng m t c nh và hai góc k c a tam giác kia thìế ộ ạ ề ủ ằ ộ ạ ề ủ
hai tam giác đó b ng nhau.ằ
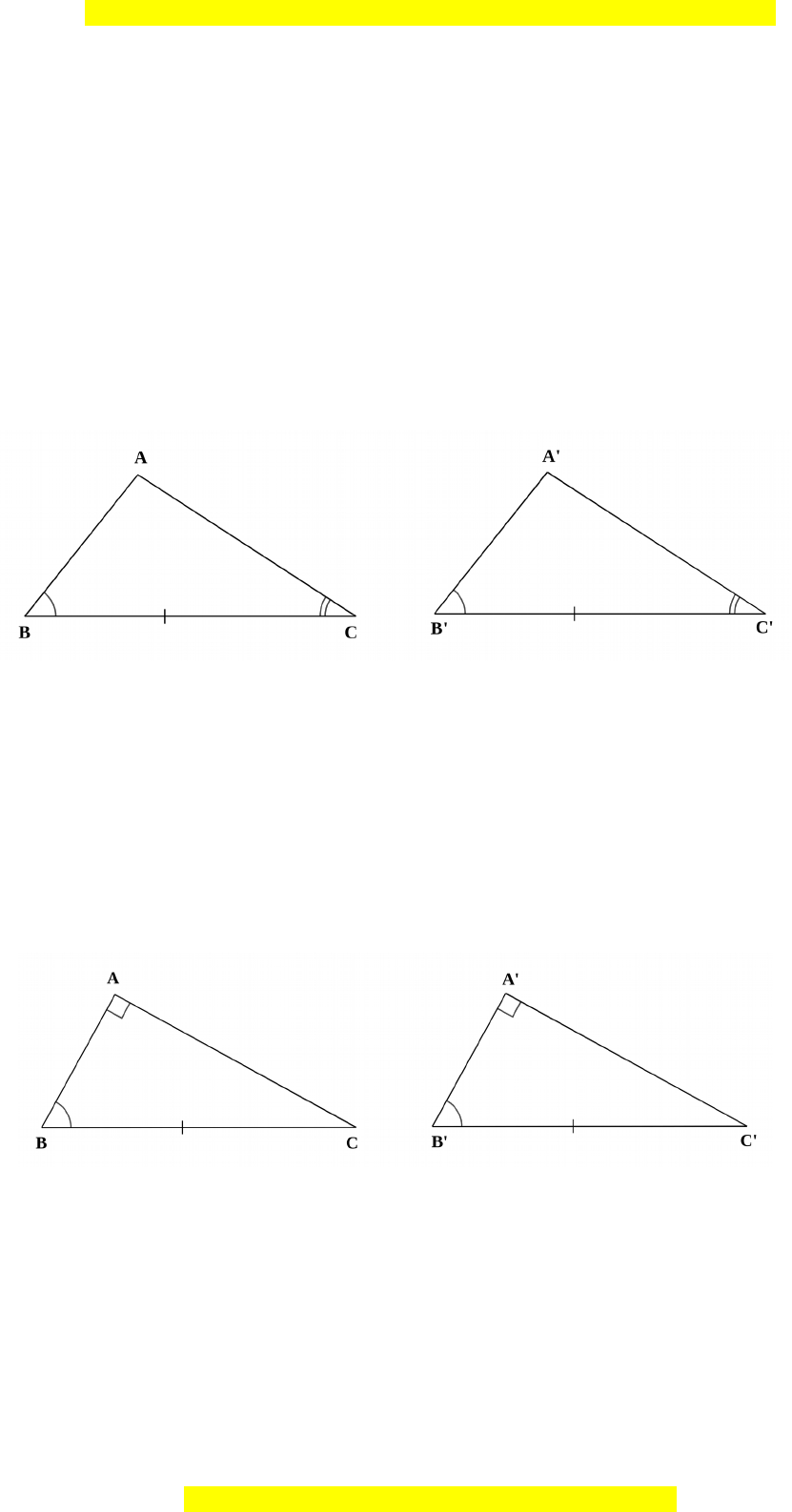
Ví d 1: ụ Cho hai tam giác
ABC
và
A B C
có:
B B
BC B C
C C
ABC A B C
(g – c – g).
2. Tr ng h p b ng nhau c nh huy n – góc nh n c a hai tam giác vuôngườ ợ ằ ạ ề ọ ủ
N u c nh huy n và m t góc nh n c a tam giác vuông này b ng c nh huy n và m t góc nh n ế ạ ề ộ ọ ủ ằ ạ ề ộ ọ
c a tam giác vuông kia thì hai tam giác vuông đó b ng nhau.ủ ằ
Ví d 1: ụ Cho hai tam giác
ABC
và
A B C
có:
90A A
BC B C
B B
ABC A B C
(c nh huy n – góc nh n).ạ ề ọ
3. Các d ng toán th ng g pạ ườ ặ
D ng 1. Ch ng minh hai tam giác b ng nhau theo tr ng h p góc – c nh – góc.ạ ứ ằ ườ ợ ạ
Ph ng pháp:ươ
S d ng tr ng h p b ng nhau góc – c nh – góc c a tam giác và tr ng h p b ng nhau c nh ử ụ ườ ợ ằ ạ ủ ườ ợ ằ ạ
huy n – góc nh n c a tam giác vuông.ề ọ ủ
D ng 2. Ch ng minh hai đo n th ng b ng nhau. Tính đ dài đo n th ng.ạ ứ ạ ẳ ằ ộ ạ ẳ
Ph ng pháp:ươ
+ Ch n hai tam giác ch a các đo n th ng c n tính.ọ ứ ạ ẳ ầ
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ

Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
+ Ch ng minh hai tam giác b ng nhau theo tr ng h p góc c nh góc.ứ ằ ườ ợ ạ
+ Suy ra các y u t c n thi t đ gi i bài toán.ế ố ầ ế ể ả
D ng 3. Bài toán s d ng nhi u tr ng h p b ng nhau c a tam giác.ạ ử ụ ề ườ ợ ằ ủ
Ph ng pháp:ươ
S d ng các tr ng h p b ng nhau đã h c c a tam giác: c nh – c nh – c nh, c nh – góc – ử ụ ườ ợ ằ ọ ủ ạ ạ ạ ạ
c nh, góc – c nh – góc ... và các tr ng h p b ng nhau c a tam giác vuông.ạ ạ ườ ợ ằ ủ
II. PH N TR C NGHI MẦ Ắ Ệ
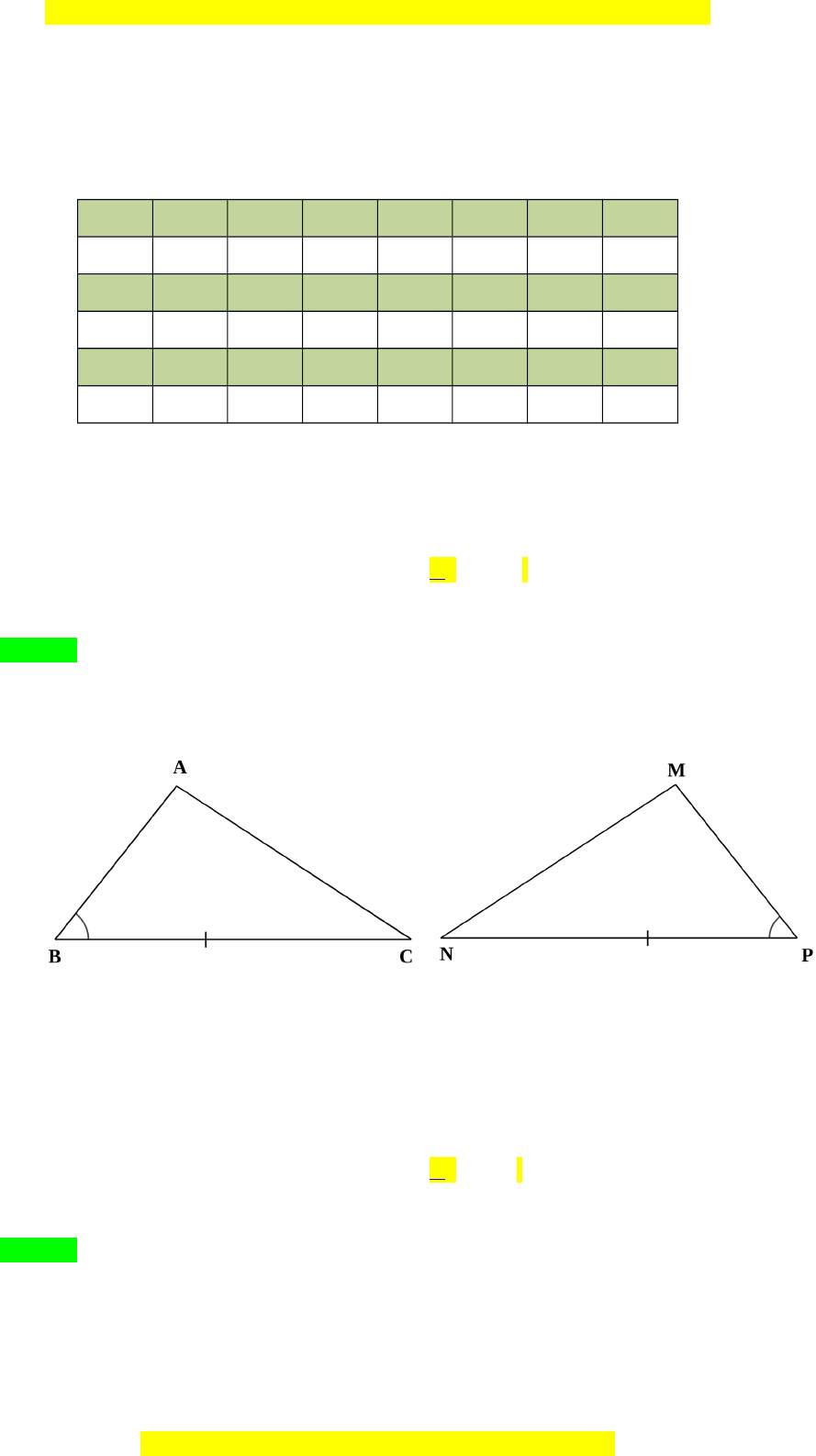
Câu 1. Cho tam giác
ABC
và tam giác
NPM
có
BC PM
;
B P
. C n thêm m t đi u ki n gì đầ ộ ề ệ ể
tam giác
MPN
và tam giác
CBA
b ng nhau theo tr ng h p góc – c nh – góc?ằ ườ ợ ạ
A.
M A
. B.
A P
. C.
C M
. D.
A N
.
Câu 2. Cho tam giác
ABC
và tam giác
DEF
có
BC EF
;
B F
. C n thêm m t đi u ki n gì đầ ộ ề ệ ể
tam giác
ABC
và tam giác
DFE
b ng nhau theo tr ng h p góc – c nh – góc?ằ ườ ợ ạ
A.
A E
. B.
A D
. C.
C E
. D.
C D
.
Câu 3. Cho tam giác
ABC
và tam giác
MNP
có
A M
;
B N
. C n thêm đi u ki n gì đ tam giácầ ề ệ ể
ABC
và tam giác
MNP
b ng nhau theo tr ng h p góc – c nh – góc?ằ ườ ợ ạ
A.
AC MP
. B.
AB MN
. C.
BC NP
. D.
AC MN
.
Câu 4. Cho tam giác
IKQ
và tam giác
MNP
có
I M
;
K P
. C n thêm đi u ki n gì đ tam giácầ ề ệ ể
IKQ
và tam giác
MNP
b ng nhau theo tr ng h p góc – c nh – góc?ằ ườ ợ ạ
A.
IQ MN
. B.
IK MP
. C.
QK NP
. D.
IK MN
.
Câu 5. Cho tam giác
PQR
và tam giác
DEF
có
60 , ,P D PR DE R E
. Phát bi u nào trongể
các phát bi u sau đây là đúng:ể
A.
PQR DEF
B.
PQR DEF
. C.
RQP FDE
. D.
PQR DFE
.
Câu 6. Cho góc nh nọ
,xOy Oz
là tia phân giác c a góc đó. Qua đi m A thu c tia ủ ể ộ
Ox
k đ ng th ngẻ ườ ẳ
song song v i ớ
Oy
c t ắ
Oz
t i ạ
M
. Qua
M
k đ ng th ng song song v i ẻ ườ ẳ ớ
Ox
c t ắ
Oy
ở
B
.
Ch n câu đúng.ọ
A.
;OA OB MA MB
B.
;OA OB MA MB
C.
;OA OB MA MB
D.
;OA OB MA MB
.
Câu 7. Cho góc nh nọ
,xOy Oz
là tia phân giác c a góc đó. Trên ủ
Oz
l y đi m ấ ể
E
, v đ ng th ngẽ ườ ẳ
qua
E
vuông góc v i ớ
Ox
t i ạ
K
, c t ắ
Oy
t i ạ
N
. V đ ng th ng qua ẽ ườ ẳ
E
vuông góc v i ớ
Oy
t i ạ
H
c t ắ
Ox
t i ạ
M
. Ch n câu đúng.ọ
A.
;OK OH KN HM
B.
;OK OH KN HM
C.
;OK OH KN HM
D.
;OK OH KN HM
.
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ

Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Câu 8. Cho đo n th ng ạ ẳ
,AB O
là trung đi m c a ể ủ
AB
. Trên cùng m t n a m t ph ng b ộ ử ặ ẳ ờ
AB
v cácẽ
tia
;Ax By
vuông góc v i ớ
AB
. G i ọ
C
là đi m thu c tia ể ộ
Ax
. Đ ng vuông góc v i ườ ớ
OC
t iạ
O
c t tia ắ
By
t i ạ
D
. Khi đó
A.
BD CD AC
. B.
AC CD BD
. C.
CD AC BD
D.
CD AC BD
.
Câu 9. Cho tam giác
ABC
có
AB AC
. Trên các c nh ạ
AB
và
AC
l y các đi m ấ ể
,D E
sao cho
AD AE
. G i ọ
K
là giao đi m c a ể ủ
BE
và
CD
. Ch n câu sai.ọ
A.
BE CD
. B.
BK CK
. C.
BD CE
. D.
DK KC
.
Câu 10. Cho tam giác
ABC
có
AB AC
. Tia phân giác c a góc ủ
A
c t ắ
BC
Ở
K
. T ừ
B
k đ ngẻ ườ
vuông góc v i ớ
AK
t i ạ
H
c t ắ
AC
ở
D
. Ch n câu sai.ọ
A.
HB HD
. B.
HB AD
. C.
AB AD
. D.
ABH ADH
.
Câu 11. Cho tam giác
DEF
và tam giác
HKG
có
; ;D H E K DE HK
. Bi t ế
80F
. S đo gócố
G
là:
A.
70
. B.
80
. C.
90
. D.
100
.
Câu 12. Cho tam giác
DEF
và tam giác
HKG
có
D K
,
E G
,
DE KG
. Bi t ế
75F
. S đoố
góc
H
là:
A.
70
. B.
75
. C.
90
. D.
100
Câu 13. Cho tam giác
ABC
và tam giác
DEF
có
, ,AB DE B E A D
. Bi t ế
6AC cm
. Đ dàiộ
DF
là:
A.
4cm
. B.
5cm
. C.
6cm
. D.
7cm
.
Câu 14. Cho
ABC
và
DEF
có
, ,AB DE B E A D
. Bi t ế
6AC cm
. Đ dài ộ
DF
là
A.
4 cm
. B.
5 cm
. C.
6 cm
. D.
7 cm
.
Câu 15. Cho
ABC
vuông t i ạ
A
có
AB AC
. Qua
A
k đ ng th ng ẻ ườ ẳ
xy
sao cho
,B C
n m cùngằ
phía v i ớ
xy
. K ẻ
,BD CE
vuông góc v i ớ
xy
. Ch n câu đúng?ọ
A.
DE BD CE
. B.
DE BD CE
. C.
CE BD DE
. D.
CE BD DE
.
Câu 16. Cho
ABC
có
D
là trung đi m c a ể ủ
AB
. Qua
D
k đ ng th ng song song v i ẻ ườ ẳ ớ
BC
, c tắ
AC
t i ạ
E
, đ ng th ng qua ườ ẳ
E
và song song v i ớ
AB
, c t ắ
BC
t i ạ
F
. Khi đó
A.
ADE EFC
. B.
ADE DBF
.
C.
EFC DBF
. D. C ba đáp án đ u đúngả ề .
Câu 17. Cho
ABC
có
60A
. Tia phân giác góc
B
c t c a ắ ủ
AC
t i đi m ạ ể
D
. Tia phân giác góc
C
c t c a ắ ủ
AB
t i đi m ạ ể
E
. Các tia phân giác đó c t nhau t i ắ ạ
I
. Tính đ dài ộ
ID
, bi t ế
2 cmIE
.
A.
4 cmID
. B.
2 cmID
. C.
8 cmID
. D.
3 cmID
.
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ

Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Câu 18. Hai đo n th ng ạ ẳ
,AB CD
song song v i nhau. Hai đo n th ng này ch n gi a hai đ ng th ngớ ạ ẳ ắ ữ ườ ẳ
song song
,AC BD
. Ch n câu đúng.ọ
A.
4 cmID
. B.
2 cmID
. C.
8 cmID
. D.
3 cmID
.
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
BÀI 5
TR NG H P B NG NHAU TH BA C A TAM GIÁC ƯỜ Ợ Ằ Ứ Ủ
GÓC – C NH – GÓCẠ
B NG TR L IẢ Ả Ờ
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8
C C B B D B D D
Câu 9 Câu 10 Câu 11 Câu 12 Câu 13 Câu 14 Câu 15 Câu 16
D B B B C C D A
Câu 17 Câu 18 Câu 19 Câu 20 Câu 21 Câu 22 Câu 23 Câu 24
B A
H NG D N GI I CHI TI TƯỚ Ẫ Ả Ế
Câu 1. Cho tam giác
ABC
và tam giác
NPM
có
BC PM
;
B P
. C n thêm m t đi u ki n gì đầ ộ ề ệ ể
tam giác
MPN
và tam giác
CBA
b ng nhau theo tr ng h p góc – c nh – góc?ằ ườ ợ ạ
A.
M A
. B.
A P
. C.
C M
. D.
A N
.
L i gi iờ ả
Ch n Cọ
Áp d ng tr ng h p b ng nhau th ba c a tam giác: N u m t c nh và hai góc k c a tam ụ ườ ợ ằ ứ ủ ế ộ ạ ề ủ
giác này b ng m t c nh và hai góc k c a tam giác kia thì hai tam giác đó b ng nhau.ằ ộ ạ ề ủ ằ
Áp d ng tr ng h p b ng nhau th ba c a tam giác góc – c nh – góc, ta th y đ tam giácụ ườ ợ ằ ứ ủ ạ ấ ể
MPN
và tam giác
CBA
b ng nhau ta c n thêm m t đi u ki n là ằ ầ ộ ề ệ
C M
.
Câu 2. Cho tam giác
ABC
và tam giác
DEF
có
BC EF
;
B F
. C n thêm m t đi u ki n gì đầ ộ ề ệ ể
tam giác
ABC
và tam giác
DFE
b ng nhau theo tr ng h p góc – c nh – góc?ằ ườ ợ ạ
A.
A E
. B.
A D
. C.
C E
. D.
C D
.
L i gi iờ ả
Ch n Cọ
Áp d ng tr ng h p b ng nhau th ba c a tam giác: N u m t c nh và hai góc k c a tam ụ ườ ợ ằ ứ ủ ế ộ ạ ề ủ
giác này b ng m t c nh và hai góc k c a tam giác kia thì hai tam giác đó b ng nhau.ằ ộ ạ ề ủ ằ
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ