Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) BÀI 4. TRƯ N Ờ G HỢP B N Ằ G NHAU TH N Ứ H T Ấ C A Ủ TAM GIÁC: C N Ạ H - C N Ạ H – C N Ạ H A. TÓM T T Ắ LÝ THUY T Ế 1. Trư n ờ g h p ợ b n ằ g nhau c n ạ h – c n ạ h – c n ạ h (c.c.c) Nếu ba cạnh c a
ủ tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó b ng nha ằ u.
ΔABC và ΔA'B'C' có : AC = A'C' BC = B'C'Δ
ABC = ΔA'B'C'(c.c.c) AB = A'B' 2. Trư n ờ g h p ợ b n ằ g nhau v c ề n ạ h huy n ề và c n ạ h góc vuông c a ủ tam giác vuông. Nếu cạnh huyền và m t ộ cạnh góc vuông c a
ủ tam giác vuông này b ng c ằ nh huy ạ n và ề m t ộ c nh góc ạ
vuông của tam giác vuông kia thì hai tam giác vuông đó b ng nha ằ u.
ΔABC và ΔA'B'C' có: µ µ o A A ' 90 AB A 'B' BC B'C '
ΔABC = ΔA'B'C' ( cạnh huyền–cạnh góc vuông) B. BÀI T P Ậ TR C Ắ NGHI M Ệ Hãy ch n
ọ đáp án đúng t c ừ âu 1 đ n ế câu 11.
Câu 1. Hai tam giác bằng nhau theo trư ng h ờ p c ợ
ạnh – cạnh – cạnh khi có:
A. hai cặp cạnh bằng nhau .
B. một cặp cạnh bằng nhau .
C. ba cặp cạnh bằng nhau .
D. ba cặp cạnh bằng nhau và ba cặp góc bằng nhau .
Câu 2. ΔABC và ΔMPN có AB = MN; BC = NP; AC = MP
. Khi đó hai tam giác bằng nhau là:
A. ΔBAC và ΔMNP . B. ΔACB v à ΔMNP . C. ΔCBA v à ΔPMN .
D. ΔABC và ΔMNP ΔDEF ΔDEF ΔPQR Câu 3.
và ΔPQR có ED = QP;DF = PR . Điều ki n đ ệ ể = là A. EF = RP . B. FE = RQ . C. QR = DF . D. EF = PQ . M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
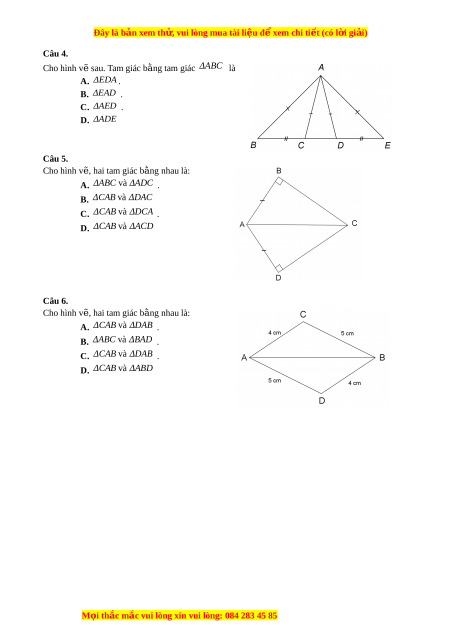
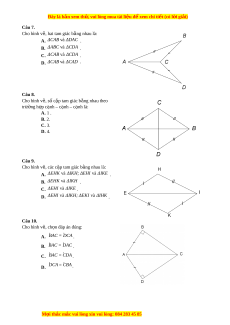
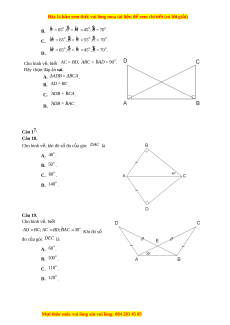
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) Câu 4. Cho hình v s ẽ au. Tam giác b ng t ằ am giác ΔABC là A. ΔEDA . B. ΔEAD . C. ΔAED . D. ΔADE Câu 5. Cho hình v , ha ẽ i tam giác bằng nhau là: A. ΔABC v à ΔADC . B. ΔCAB v à ΔDAC C. ΔCAB v à ΔDCA . D. ΔCAB v à ΔACD Câu 6. Cho hình v , ha ẽ i tam giác bằng nhau là: A. ΔCAB v à ΔDAB . B. ΔABC v à ΔBAD . C. ΔCAB v à ΔDAB . D. ΔCAB v à ΔABD M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
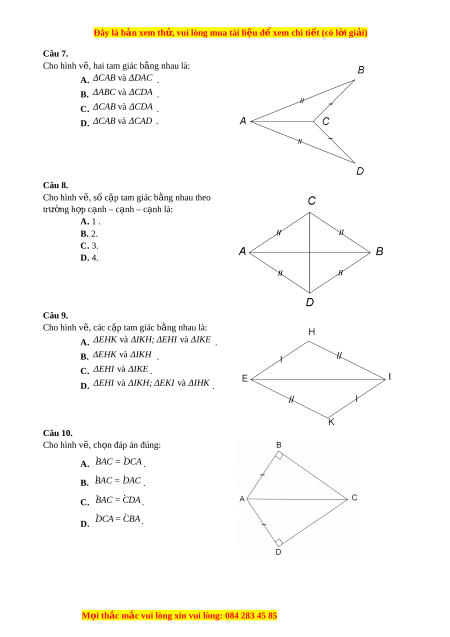
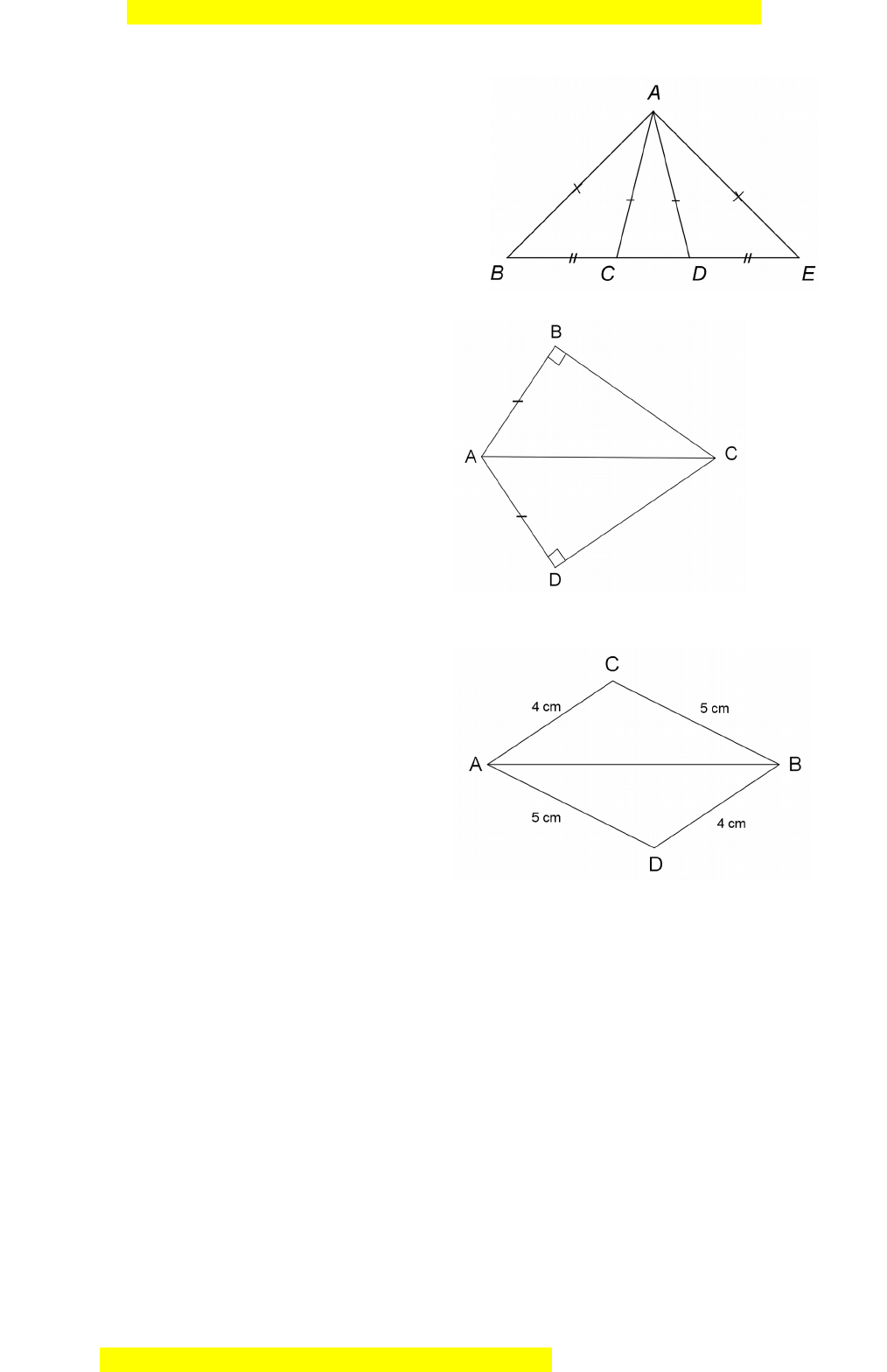
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) Câu 7. Cho hình v , ha ẽ i tam giác bằng nhau là:
A. ΔCAB và ΔDAC . B. ΔABC v à ΔCDA . C. ΔCAB v à ΔCDA . D. ΔCAB v à ΔCAD . Câu 8. Cho hình v , s ẽ c
ố ặp tam giác bằng nhau theo trư ng h ờ p c ợ
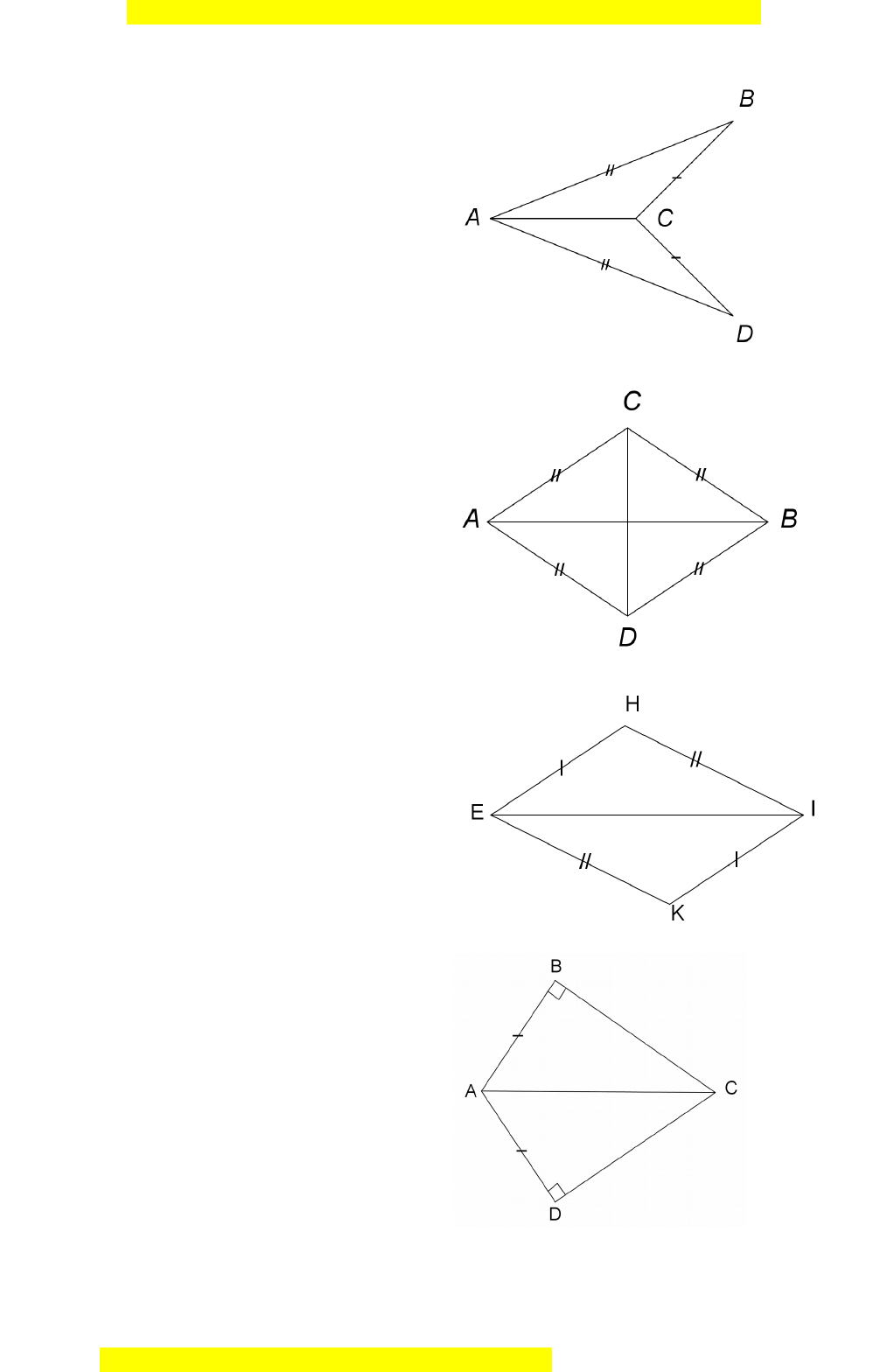
ạnh – cạnh – cạnh là: A. 1 . B. 2. C. 3. D. 4. Câu 9. Cho hình v , c
ẽ ác cặp tam giác bằng nhau là: A. ΔEHK v
à ΔIKH; ΔEHI và ΔIKE .
B. ΔEHK và ΔIKH .
C. ΔEHI và ΔIKE .
D. ΔEHI và ΔIKH; ΔEKI và ΔIHK . Câu 10. Cho hình v , c ẽ h n đá ọ p án đúng: · · A. BAC = DCA . · · B. BAC = DAC . · · C. BAC = CDA . · · DCA = CBA D. . M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
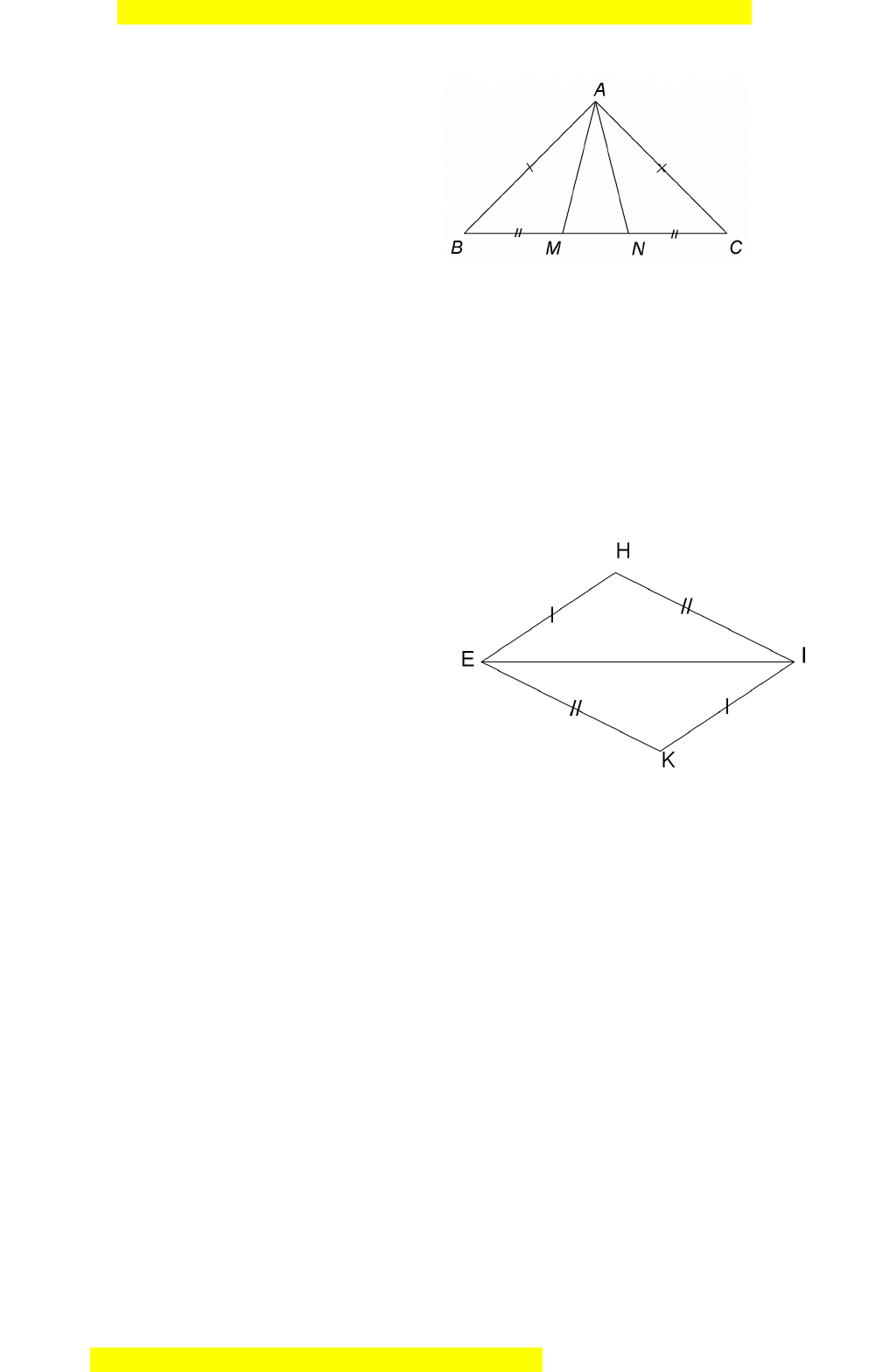
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) Câu 11. Cho hình v , c
ẽ ác cặp tam giác bằng nhau là A. ΔABM v
à ΔACN; ΔABN và ΔACM
B. ΔAMC và ΔABN; ΔABM và ΔACN C. ΔABM v à ΔACN .
ΔAMC ΔABN; ΔABM ΔAMN D. và và
Câu 12. Cho hai tam giác ABD và CDB có cạnh chung là BD . Bi t
ế AB = CD và AD = CB . Phát
biểu nào sau đây sai?
A. ΔABD = ΔCDB . · · B. BAD = BCD . · · C. DBA = DBC . · · D. BDC = DBA . Câu 13. Cho hình v , c ẽ h n đá ọ p án sai:
A. ΔEKI = ΔIHE .
B. EK / / HI .
C. ΔEKI = ΔHIE .
D. EH / / KI .
.Câu 14. Cho tam giác ABC có AB = AC và I là trung đi m ể c a
ủ BC . Khi đó đáp án đúng là:
A. ΔAIB = ΔACI . · · B. ABI = AIC . C. AI = CI .
D. AI là tia phân giác của góc BAC .
Câu 15. Cho tam giác ABC có AB = AC và M là trung đi m ể c a
ủ BC . Khi đó số đo góc AMB bằng o A. 1 80 . o B. 90 . o C. 60 . o D. 45 . o o $ $
Câu 16. Cho hai tam giác ABC và MNP có AB = MN, BC = NP, AC = MP, A = 6 5 , P = 7 0 . Khi đó s đo c ố ác góc còn lại c a ủ hai tam giác là µ o $ µ o o $ A. M = 65
, B = N = 45 ,C = 7 0 . M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Chuyên đề Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh Toán 7 Cánh diều
542
271 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Bài tập Chuyên đề Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh Toán lớp 7 Cánh diều được biên soạn theo các mức độ, có lời giải nhằm giúp Giáo viên có thêm tài liệu tham khảo.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(542 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 7
Xem thêmTài liệu bộ mới nhất

Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
BÀI 4. TR NG H P B NG NHAU TH NH T C A TAM GIÁC: C NH - C NH – ƯỜ Ợ Ằ Ứ Ấ Ủ Ạ Ạ
C NHẠ
A. TÓM T T LÝ THUY TẮ Ế
1. Tr ng h p b ng nhau c nh – c nh – c nh (c.c.c) ườ ợ ằ ạ ạ ạ
N u ba c nh c a tam giác này b ng ba c nh c a tam giác kia thì hai tam giác đó b ng nhau.ế ạ ủ ằ ạ ủ ằ
ΔABC và ΔA'B'C' có :
AC = A'C'
BC = B'C'ΔABC = ΔA'B'C'(c.c.c)
AB = A'B'
2. Tr ng h p b ng nhau v c nh huy n và c nh góc vuông c a tam giác vuông.ườ ợ ằ ề ạ ề ạ ủ
N u c nh huy n và m t c nh góc vuông c a tam giác vuông này b ng c nh huy n và m t c nh gócế ạ ề ộ ạ ủ ằ ạ ề ộ ạ
vuông c a tam giác vuông kia thì hai tam giác vuông đó b ng nhau.ủ ằ
ΔABC
và
ΔA'B'C'
có:
µ µ
o
A A ' 90
AB A ' B'
BC B'C '
ΔABC = ΔA'B'C'
( c nh huy n–c nh góc ạ ề ạ
vuông)
B. BÀI T P TR C NGHI MẬ Ắ Ệ
Hãy ch n đáp án đúng t câu 1 đ n câu ọ ừ ế 11.
Câu 1. Hai tam giác b ng nhau theo tr ng h p c nh – c nh – c nh khi có:ằ ườ ợ ạ ạ ạ
A. hai c p c nh b ng nhau ặ ạ ằ .
B. m t c p c nh b ng nhauộ ặ ạ ằ .
C. ba c p c nh b ng nhauặ ạ ằ .
D. ba c p c nh b ng nhau và ba c p góc b ng nhauặ ạ ằ ặ ằ .
Câu 2.
ΔABC
và
ΔMPN
có
AB = MN; BC = NP; AC = MP
. Khi đó hai tam giác b ng nhau là:ằ
A.
vàΔBAC ΔMNP
.
B.
và ΔACB ΔMNP
.
C.
vàΔCBA ΔPMN
.
D.
vàΔABC ΔMNP
Câu 3.
ΔDEF
và
ΔPQR
có
ED = QP;DF = PR .
Đi u ki n đ ề ệ ể
=ΔDEF ΔPQR
là
A.
EF = RP
.
B.
FE = RQ
.
C.
QR = DF
.
D.
EF = PQ
.
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Câu 4.
Cho hình v sau. Tam giác b ng tam giác ẽ ằ
ΔABC
là
A.
ΔEDA
.
B.
ΔEAD
.
C.
ΔAED
.
D.
ΔADE
Câu 5.
Cho hình v , hai tam giác b ng nhau là:ẽ ằ
A.
vàΔABC ΔADC
.
B.
vàΔCAB ΔDAC
C.
vàΔCAB ΔDCA
.
D.
vàΔCAB ΔACD
Câu 6.
Cho hình v , hai tam giác b ng nhau là:ẽ ằ
A.
vàΔCAB ΔDAB
.
B.
vàΔABC ΔBAD
.
C.
vàΔCAB ΔDAB
.
D.
vàΔCAB ΔABD
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Câu 7.
Cho hình v , hai tam giác b ng nhau là:ẽ ằ
A.
vàΔCAB ΔDAC
.
B.
vàΔABC ΔCDA
.
C.
vàΔCAB ΔCDA
.
D.
vàΔCAB ΔCAD .
Câu 8.
Cho hình v , s c p tam giác b ng nhau theo ẽ ố ặ ằ
tr ng h p c nh – c nh – c nh là:ườ ợ ạ ạ ạ
A. 1
.
B. 2.
C. 3.
D. 4.
Câu 9.
Cho hình v , các c p tam giác b ng nhau là:ẽ ặ ằ
A.
và vàΔEHK ΔIKH; ΔEHI ΔIKE
.
B.
vàΔEHK ΔIKH
.
C.
vàΔEHI ΔIKE
.
D.
và vàΔEHI ΔIKH; ΔEKI ΔIHK
.
Câu 10.
Cho hình v , ch n đáp án đúng:ẽ ọ
A.
·
·
BAC = DCA
.
B.
·
·
BAC = DAC
.
C.
·
·
BAC = CDA
.
D.
·
·
DCA = CBA
.
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
Câu 11.
Cho hình v , các c p tam giác b ng nhau làẽ ặ ằ
A.
và vàΔABM ΔACN; ΔABN ΔACM
B.
và vàΔAMC ΔABN; ΔABM ΔACN
C.
và ΔABM ΔACN
.
D.
và vàΔAMC ΔABN; ΔABM ΔAMN
Câu 12. Cho hai tam giác
vàABD CDB
có c nh chung là ạ
BD
. Bi t ế
AB = CD
và
AD = CB
. Phát
bi u nào sau đây ể sai?
A.
ΔABD = ΔCDB
.
B.
·
·
BAD = BCD
.
C.
·
·
DBA = DBC
.
D.
·
·
BDC = DBA
.
Câu 13.
Cho hình v , ch n đáp án ẽ ọ sai:
A.
ΔEKI = ΔIHE
.
B.
// EK HI
.
C.
ΔEKI = ΔHIE
.
D.
// EH KI
.
.Câu 14. Cho tam giác
ABC
có
AB = AC
và
I
là trung đi m c a ể ủ
BC
. Khi đó đáp án đúng là:
A.
ΔAIB = ΔACI
.
B.
· ·
ABI = AIC
.
C.
AI = CI
.
D.
AI
là tia phân giác c a gócủ
BAC
.
Câu 15. Cho tam giác
ABC
có
AB = AC
và
M
là trung đi m c a ể ủ
BC
. Khi đó s đo gócố
AMB
b ngằ
A.
o
180
.
B.
o
90
.
C.
o
60
.
D.
o
45
.
Câu 16. Cho hai tam giác
ABC
và
MNP
có
o o
, .
65 70
$ $
AB = MN, BC = NP, AC = MP, A = P =
Khi
đó s đo các góc còn l i c a hai tam giác làố ạ ủ
A.
µ
µ
o o o
.
65 45 70
$ $
, = ,
M = B = N C =
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ
Đây là b n xem th , vui lòng mua tài li u đ xem chi ti t (có l i gi i)ả ử ệ ể ế ờ ả
B.
µ
µ
o o o
, , .65 45 70
$ $
N = C = M B =
C.
µ
µ
o o o
, , .
65 55 70
$ $
M = B = N C =
D.
µ
µ
o o o
, , .65 45 70
$ $
M = C = N B =
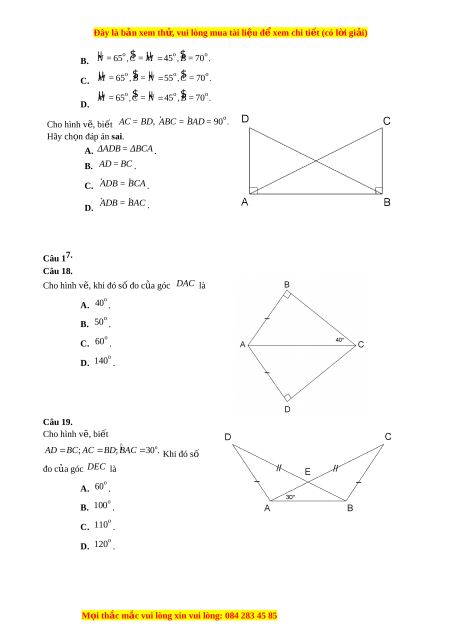
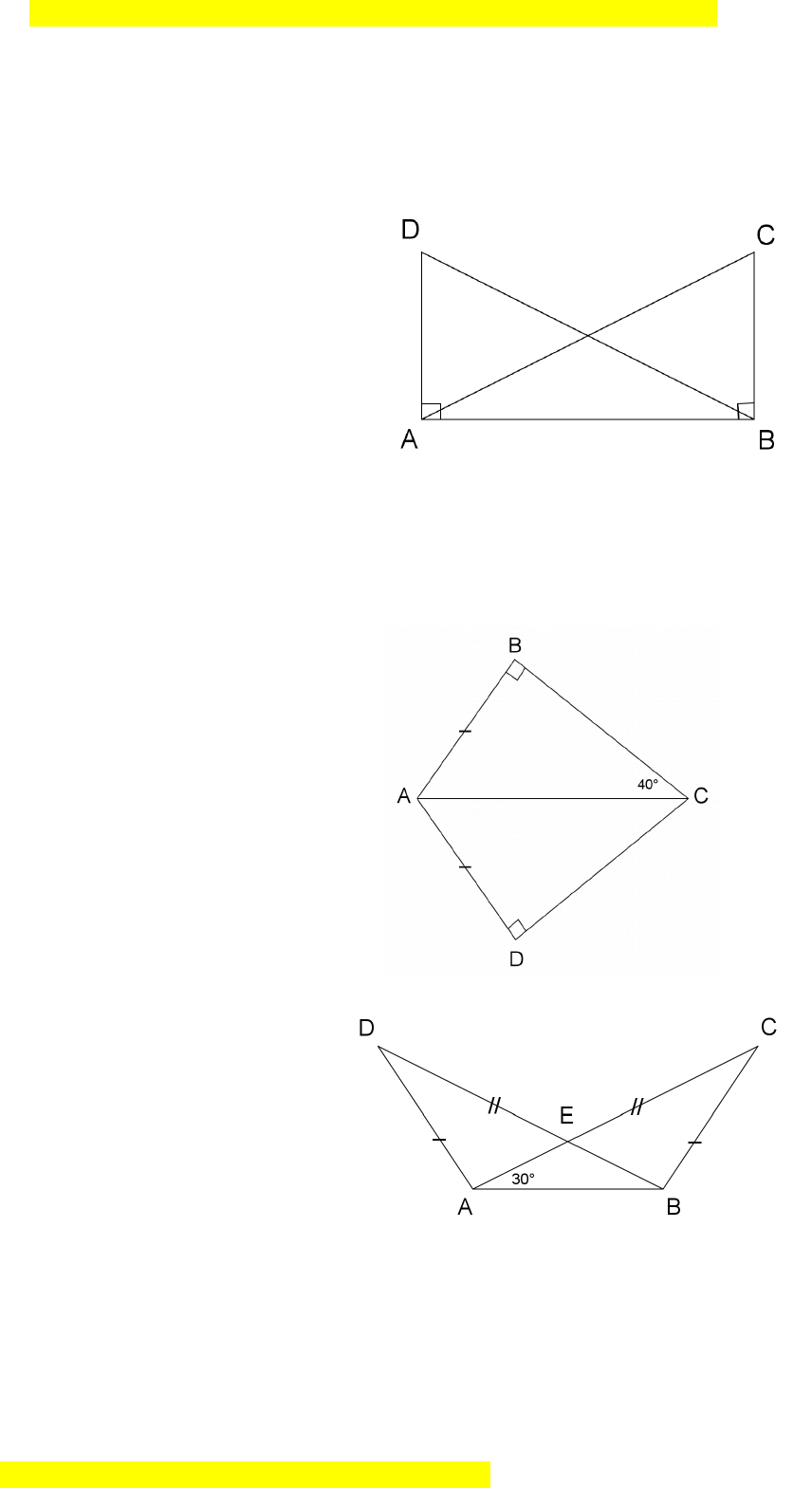
Cho hình v , bi t ẽ ế
·
·
o
.
90 AC = BD, ABC = BAD =
Hãy ch n đáp án ọ sai.
A.
ΔADB = ΔBCA
.
B.
= AD BC
.
C.
·
·
ADB = BCA
.
D.
·
·
ADB = BAC
.
Câu 1
7.
Câu 18.
Cho hình v , khi đó s đo c a góc ẽ ố ủ
DAC
là
A.
o
40
.
B.
o
50
.
C.
o
60
.
D.
o
140
.
Câu 19.
Cho hình v , bi tẽ ế
o
; ; 30 . AD BC AC BD BAC
Khi đó s ố
đo c a gócủ
DEC
là
A.
o
60
.
B.
o
100
.
C.
o
110
.
D.
o
120
.
M i th c m c vui lòng xin vui lòng: 084 283 45 85ọ ắ ắ