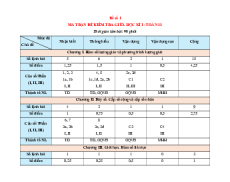
SỞ GIÁO DỤC & ĐÀO TẠO …
KIỂM TRA GIỮA HỌC KÌ 1 TRƯỜNG …
MÔN: TOÁN – LỚP 11 MÃ ĐỀ MT103 Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Một cung tròn có độ dài bằng bán kính. Khi đó số đo bằng radian của cung tròn đó là A. 1; B. 2; C. ; D. 2 .
Câu 2. Trong mặt phẳng tọa độ Oxy , trên đường tròn lượng giác như hình vẽ.
Cho góc lượng giác có tia đầu là OA và số đo là 135
. Tia cuối của góc lượng giác
đã cho là tia nào sau đây? A. OM ; B. ON ; C. OP ; D. OQ .
Câu 3. Một góc lượng giác có điểm cuối ở góc phần tư thứ II thì A. sin sin ; B. 2 sin sin ; C. 2 cos cos ; D. tan 0 .
Câu 4. Giá trị của cos 2k 1 là 4 A. k 3 cos 2 1 ; B. k 2 cos 2 1 ; 4 2 4 2 C. k 1 cos 2 1 ; D. k 3 cos 2 1 . 4 2 4 2
Câu 5. Cho góc thỏa mãn 1 cot
. Giá trị của biểu thức 3sin 4cos P là 3 2sin 5cos 15 15 A. P ; B. P ; C. P 13 ; D. P 13 . 13 13
Câu 6. Rút gọn biểu thức M cosa bcosa b sin a bsin a b ta được A. 2
M 1 2cos a ; B. 2
M 1 2sin a ; C. 2
M 1 2cos b ; D. 2
M 1 2sin b .
Câu 7. Khẳng định nào sau đây là sai?
A. Hàm số y sin x là hàm số lẻ;
B. Hàm số y cos x là hàm số lẻ;
C. Hàm số y tan x là hàm số lẻ;
D. Hàm số y cot x là hàm số lẻ.
Câu 8. Hàm số y tan x tuần hoàn với chu kì 1 A. ; B. ; C. 2; D. 3 . 2
Câu 9. Hàm số y tan x đồng biến trên mỗi khoảng nào sau đây với mọi k ? A. k ; k ; B. k ; k; C. k ; k ; D. k ;2 k. 2 2
Câu 10. Tập xác định D của hàm số y cos x 2 là A. D R ; B. D \ k , k Z; C. D 1 ; 1 ; D. D . Câu 11. Cho hàm số 2 2
y sin x 2cos x liên tục trên
. Gọi M và m lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho. Giá trị của M 2m bằng A. 2; B. 3; C. 4; D. 5.
Câu 12. Tất cả nghiệm của phương trình x o cos 2
cos x 60 là A. 0 o x 2 0 1 k 20 , k ; B. o o
x 60 k360 ,k ; C. o o
x 60 k360 và o o x 2
0 k360 ,k . D. o o
x 60 k360 và o o x 2 0 1 k 20 , k .
Câu 13. Công thức nghiệm x k với k là công thức nghiệm của phương trình nào sau đây? A. o tan x tan ; B. sin x sin ; C. cos x cos ; D. tan x tan .
Câu 14. Số nghiệm thuộc đoạn ;2
của phương trình sin x 1 là 4 A. 0; B. 1; C. 2; D. 3.
Câu 15. Phương trình cot 3x 1 3 có nghiệm là 1 5 1 A. x k , k ; B. x k , k ; 3 18 3 3 18 3 5 1 C. x k , k ; D. x k , k . 18 3 3 6 Câu 16. Với * n
, cho dãy số u gồm các số nguyên dương chia hết cho 7 là 7 , n
14 , 21, 28, … Công thức số hạng tổng quát của dãy số này là
A. u 7n 7 ;
B. u 7n 7 ; C. u 7n ; D. 2 u 7n . n n n n
Câu 17. Trong các dãy số u cho bởi số hạng tổng quát u sau, dãy số nào là dãy n n số giảm? 1 4 A. u ; B. u 3 ; C. 2 u n ;
D. u n 2 . n 2n n n 1 n n
Câu 18. Trong các dãy số sau, dãy số nào không bị chặn? n
A. u : u cos2n ; B. v v n 2 5 : n n n 5n ; 2 n C. k 2
: k n 4n 9 ; D. a a . n : n 1 n n
Câu 19. Trong các dãy số sau, dãy số nào không phải cấp số cộng? 1 3 5 7 9 A. ; ; ; ; ; B. 1;1;1;1;1; 2 2 2 2 2 C. 8 ; 6 ; 4 ; ; 2;0; D. 3;1; 1 ; 2 ; 4 .
Câu 20. Cho cấp số cộng u có u 5
và d 3. Mệnh đề nào sau đây đúng? n 1 A. u 34 ; B. u 45; C. u 31; D. u 35 . 15 15 13 10
Câu 21. Giá của một chiếc xe ô tô lúc mới mua là 700 triệu đồng. Cứ sau mỗi năm sử
dụng, giá của chiếc xe ô tô giảm 50 triệu đồng. Giá còn lại của chiếc xe sau 5 năm sử dụng là A. 400 triệu đồng; B. 450 triệu đồng; C. 500 triệu đồng; D. 650 triệu đồng.
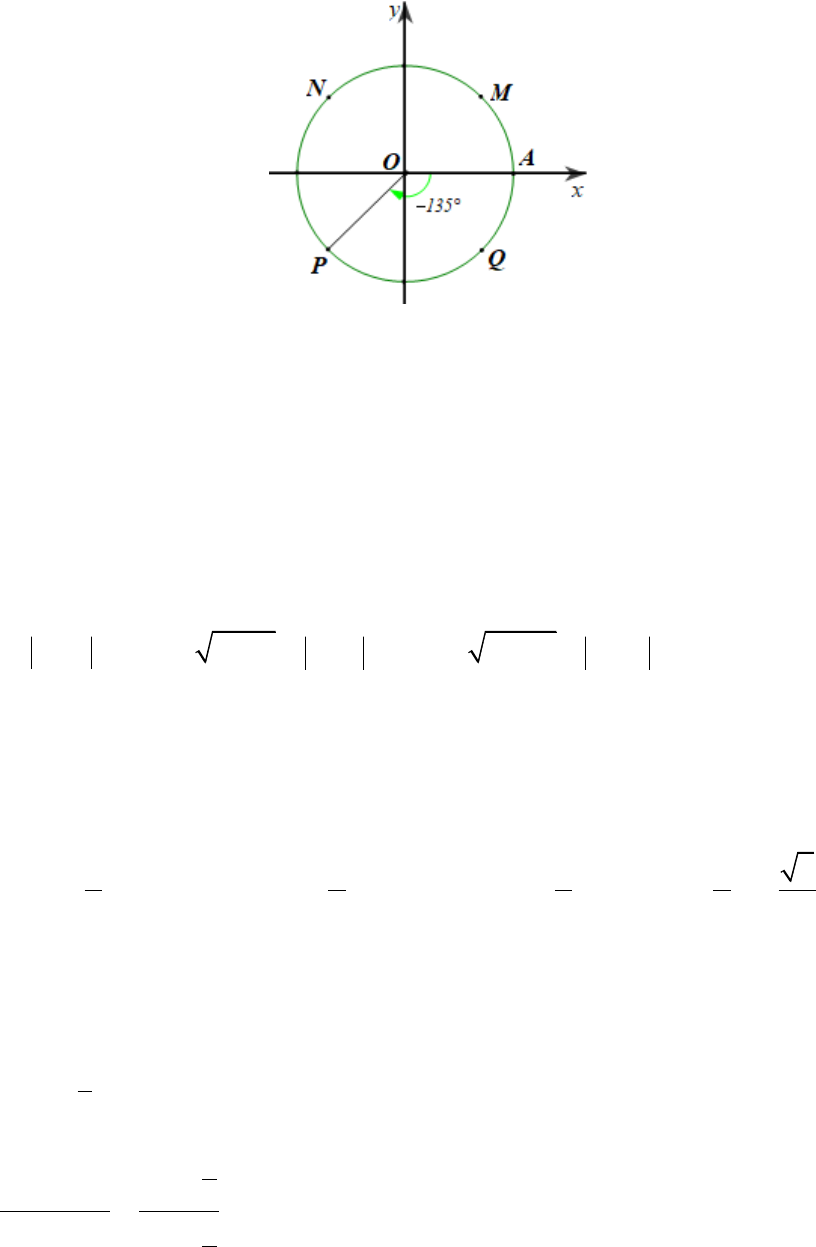
Câu 22. Cho hình chóp S.ABCD (hình vẽ). Gọi O là giao điểm của AC và BD .
Điểm O không thuộc mặt phẳng nào sau đây? A. SAC ; B. SBD ; C. SAB ; D. ABCD .
Câu 23. Cho 4 điểm không đồng phẳng ,
A B,C, D . Khi đó giao tuyến của mp ABC và mp BCD là
A. Đường thẳng AB ;
B. Đường thẳng CD ;
C. Đường thẳng BD ;
D. Đường thẳng BC .
Câu 24. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là A. 5 mặt, 5 cạnh; B. 5 mặt, 10 cạnh; C. 6 mặt, 5 cạnh; D. 6 mặt, 10 cạnh.
Câu 25. Trong các hình vẽ dưới đây, hình vẽ nào có thể là hình biểu diễn của một hình tứ diện? A. Chỉ có hình a; B. Có hai hình a và b; C. Cả ba hình a, b và c; D. Có hai hình b và c.
Câu 26. Cho tứ diện ABCD có M , N lần lượt là trung điểm của BC , AD . Gọi G
là trọng tâm của tam giác BCD . Gọi I là giao điểm của NG với mặt phẳng ABC .
Khẳng định nào sau đây đúng? A. I AM ; B. I BC ; C. I AC ; D. I AB .
Đề thi giữa kì 1 Toán 11 Cánh diều (đề 3)
0.9 K
457 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ 10 đề giữa kì 1 môn Toán 11 Cánh diều mới nhất năm 2023 - 2024 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 11.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(913 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 11
Xem thêmTài liệu bộ mới nhất
SỞ GIÁO DỤC & ĐÀO TẠO …
TRƯỜNG …
MÃ ĐỀ MT103
KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 11
Thời gian: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Câu 1. Một cung tròn có độ dài bằng bán kính. Khi đó số đo bằng radian của cung
tròn đó là
A. 1; B. 2; C.
; D.
2
.
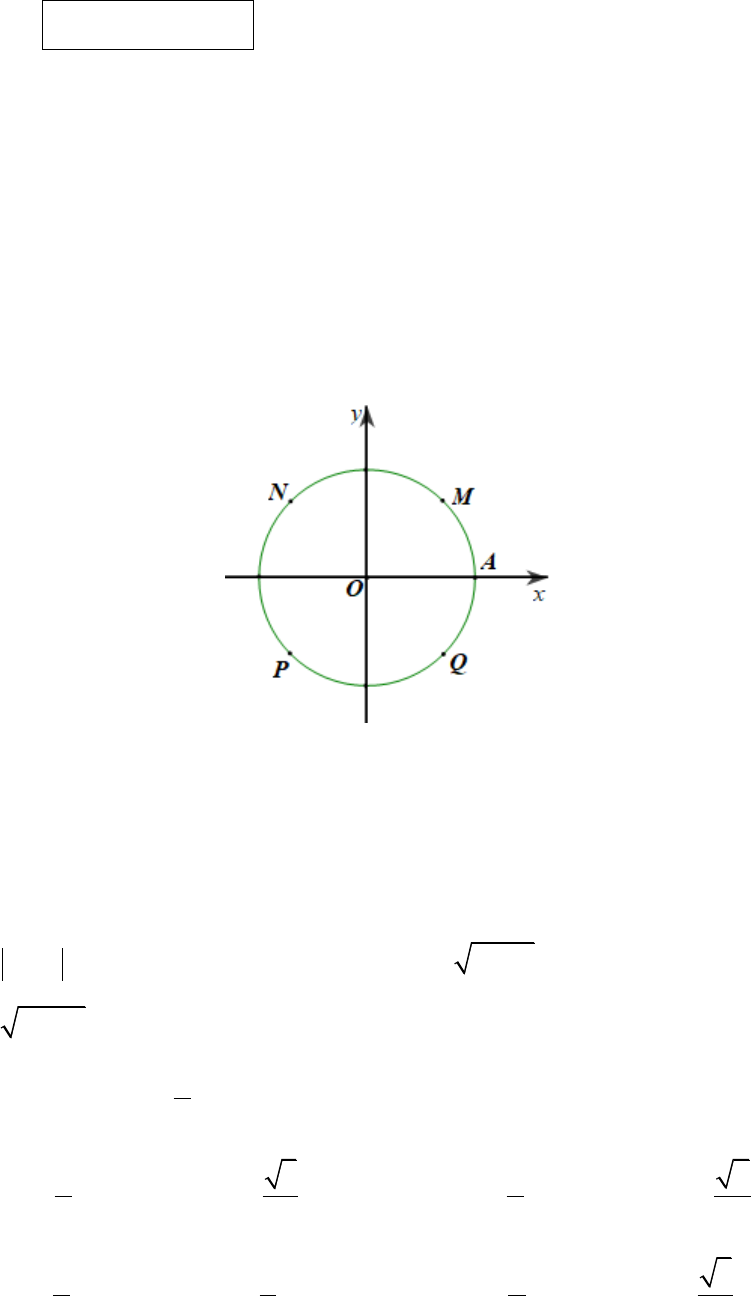
Câu 2. Trong mặt phẳng tọa độ
Oxy
, trên đường tròn lượng giác như hình vẽ.
Cho góc lượng giác có tia đầu là
OA
và số đo là
135
. Tia cuối của góc lượng giác
đã cho là tia nào sau đây?
A.
OM
; B.
ON
; C.
OP
; D.
OQ
.
Câu 3. Một góc lượng giác
có điểm cuối ở góc phần tư thứ II thì
A.
sin sin
; B.
2
sin sin
;
C.
2
cos cos
; D.
tan 0
.
Câu 4. Giá trị của
cos 2 1
4
k
là
A.
3
cos 2 1
42
k
; B.
2
cos 2 1
42
k
;
C.
1
cos 2 1
42
k
; D.
3
cos 2 1
42
k
.

Câu 5. Cho góc
thỏa mãn
1
cot
3
. Giá trị của biểu thức
3sin 4cos
2sin 5cos
P
là
A.
15
13
P
; B.
15
13
P
; C.
13P
; D.
13P
.
Câu 6. Rút gọn biểu thức
cos cos sin sinM a b a b a b a b
ta được
A.
2
1 2cosMa
; B.
2
1 2sinMa
;
C.
2
1 2cos bM
; D.
2
1 2sin bM
.
Câu 7. Khẳng định nào sau đây là sai?
A. Hàm số
sinyx
là hàm số lẻ; B. Hàm số
cosyx
là hàm số lẻ;
C. Hàm số
tanyx
là hàm số lẻ; D. Hàm số
cotyx
là hàm số lẻ.
Câu 8. Hàm số
tanyx
tuần hoàn với chu kì
A.
1
2
; B.
; C.
2
; D.
3
.
Câu 9. Hàm số
tanyx
đồng biến trên mỗi khoảng nào sau đây với mọi
k
?
A.
;kk
; B.
;kk
;
C.
;
22
kk
; D.
;2kk
.
Câu 10. Tập xác định
D
của hàm số
cos 2yx
là
A.
D R
; B.
\,D k k Z
;
C.
1;1D
; D.
D
.
Câu 11. Cho hàm số
22
sin 2cosy x x
liên tục trên . Gọi
M
và
m
lần lượt là
giá trị lớn nhất và nhỏ nhất của hàm số đã cho. Giá trị của
2Mm
bằng
A. 2; B. 3; C. 4; D. 5.
Câu 12. Tất cả nghiệm của phương trình
o
cos2 cos 60xx
là
A.
0o
20 120 ,x k k
;
B.
oo
60 360 ,x k k
;
C.
oo
60 360xk
và
oo
20 360 ,x k k
.
D.
oo
60 360xk
và
oo
20 120 ,x k k
.
Câu 13. Công thức nghiệm
xk
với
k
là công thức nghiệm của phương
trình nào sau đây?
A.
o
tan tanx
; B.
sin sinx
;
C.
cos cosx
; D.
tan tanx
.
Câu 14. Số nghiệm thuộc đoạn
;2
của phương trình
sin 1
4
x
là
A. 0; B. 1; C. 2; D. 3.
Câu 15. Phương trình
cot 3 1 3x
có nghiệm là
A.
15
,
3 18 3
x k k
; B.
1
,
3 18 3
x k k
;
C.
5
,
18 3
x k k
; D.
1
,
36
x k k
.
Câu 16. Với
*
n
, cho dãy số
n
u
gồm các số nguyên dương chia hết cho
7
là
7
,
14
,
21
,
28
, … Công thức số hạng tổng quát của dãy số này là
A.
77
n
un
; B.
77
n
un
; C.
7
n
un
; D.
2
7
n
un
.
Câu 17. Trong các dãy số
n
u
cho bởi số hạng tổng quát
n
u
sau, dãy số nào là dãy
số giảm?
A.
1
2
n
n
u
; B.
4
3
1
n
u
n
; C.
2
n
un
; D.
2
n
un
.
Câu 18. Trong các dãy số sau, dãy số nào không bị chặn?
A.
: cos 2
nn
u u n
; B.
25
:
52
nn
n
vv
n
;
C.
2
: 4 9
nn
k k n n
; D.
:1
n
nn
aa
.
Câu 19. Trong các dãy số sau, dãy số nào không phải cấp số cộng?
A.
1 3 5 7 9
;;;;
22222
; B.
1;1;1;1;1
;
C.
8; 6; 4; ;2;0
; D.
3;1; 1; 2; 4
.
Câu 20. Cho cấp số cộng
n
u
có
1
5u
và
3.d
Mệnh đề nào sau đây đúng?
A.
15
34u
; B.
15
45u
; C.
13
31u
; D.
10
35u
.
Câu 21. Giá của một chiếc xe ô tô lúc mới mua là 700 triệu đồng. Cứ sau mỗi năm sử
dụng, giá của chiếc xe ô tô giảm 50 triệu đồng. Giá còn lại của chiếc xe sau 5 năm sử
dụng là
A.
400
triệu đồng; B.
450
triệu đồng;
C.
500
triệu đồng; D.
650
triệu đồng.
Câu 22. Cho hình chóp
.S ABCD
(hình vẽ). Gọi
O
là giao điểm của
AC
và
BD
.
Điểm
O
không thuộc mặt phẳng nào sau đây?
A.
SAC
; B.
SBD
; C.
SAB
; D.
ABCD
.
Câu 23. Cho 4 điểm không đồng phẳng
, , ,A B C D
. Khi đó giao tuyến của mp
ABC
và mp
BCD
là
A. Đường thẳng
AB
; B. Đường thẳng
CD
;
C. Đường thẳng
BD
; D. Đường thẳng
BC
.
Câu 24. Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là
A.
5
mặt,
5
cạnh; B.
5
mặt,
10
cạnh;
C.
6
mặt,
5
cạnh; D.
6
mặt,
10
cạnh.
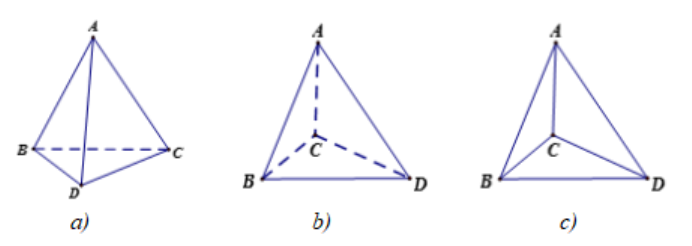
Câu 25. Trong các hình vẽ dưới đây, hình vẽ nào có thể là hình biểu diễn của một
hình tứ diện?
A. Chỉ có hình a; B. Có hai hình a và b;
C. Cả ba hình a, b và c; D. Có hai hình b và c.
Câu 26. Cho tứ diện
ABCD
có
M
,
N
lần lượt là trung điểm của
BC
,
AD
. Gọi
G
là trọng tâm của tam giác
BCD
. Gọi
I
là giao điểm của
NG
với mặt phẳng
ABC
.
Khẳng định nào sau đây đúng?
A.
I AM
; B.
I BC
; C.
I AC
; D.
I AB
.
Câu 27. Cho hình chóp
.S ABCD
có đáy là hình thang
// .ABCD AD BC
Gọi
M
là trung điểm
.CD
Giao tuyến của hai mặt phẳng
MSB
và
SAC
là
A.
SI
(
I
là giao điểm của
AC
và
BM
);
B.
SJ
(
J
là giao điểm của
AM
và
BD
);
C.
SO
(
O
là giao điểm của
AC
và
BD
);
D.
SP
(
P
là giao điểm của
AB
và
CD
).
Câu 28. Trong không gian, cho ba đường thẳng phân biệt
,,abc
trong đó
//ab
.
Khẳng định nào sau đây sai?
A. Nếu
//ac
thì
//cb
;
B. Nếu
c
cắt
a
thì
c
cắt
b
;
C. Nếu
Aa
và
Bb
thì ba đường thẳng
,,a b AB
cùng ở trên một mặt phẳng;
D. Tồn tại duy nhất một mặt phẳng qua
a
và
b
.
Câu 29. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Trong các cặp
đường thẳng sau, cặp đường thẳng nào cắt nhau?
A.
AB
và
CD
; B.
AC
và
BD
; C.
SB
và
CD
; D.
SD
và
BC
.
Câu 30. Khẳng định nào sau đây là đúng?
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song
với nhau;
B. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì trùng nhau;
C. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song
với nhau hoặc trùng nhau;
D. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì chúng lần
lượt nằm trên hai mặt phẳng song song.
Câu 31. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thang, đáy lớn là
CD
. Gọi
M
là trung điểm của
SA
,
N
là giao điểm của cạnh
SB
và mặt phẳng
MCD
. Mệnh
đề nào sau đây đúng?
A.
MN
và
SD
cắt nhau; B.
//MN CD
;
C.
MN
và
SC
cắt nhau; D.
MN
và
CD
chéo nhau.
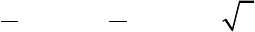
Câu 32. Cho hai đường thẳng song song
a
và
b
. Có bao nhiêu mặt phẳng chứa
a
và
song song với
b
?
A. 0; B. 1; C. 2; D. Vô số.
Câu 33. Cho mặt phẳng
và đường thẳng
d
. Khẳng định nào sau đây là
sai?
A. Nếu
//d
thì trong
tồn tại đường thẳng
sao cho
//d
;
B. Nếu
//d
và
b
thì
//bd
;
C. Nếu
dA
và
d
thì
d
và
d
hoặc cắt nhau hoặc chéo nhau;
D. Nếu
// ;d c c
thì
//d
.
Câu 34. Cho tứ diện
ABCD
. Gọi
M
,
N
lần lượt là trung điểm của
AB
và
AC
.
Đường thẳng
MN
song song với mặt phẳng
A.
ACD
; B.
ABD
; C.
BCD
; D.
ABC
.
Câu 35. Cho tứ diện
ABCD
. Gọi
G
là trọng tâm tam giác
ABD
. Trên đoạn
BC
lấy
điểm
M
sao cho
2MB MC
. Nhận định nào dưới đây là đúng?
A.
//MG ACD
; B.
MG
cắt
ACD
;
C.
//MG BCD
; D.
MG
thuộc
BCD
.
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm) Giải các phương trình lượng giác:
a)
cos 3 sin 3 3
63
xx
; b)
sin sin2 sin3 0x x x
.
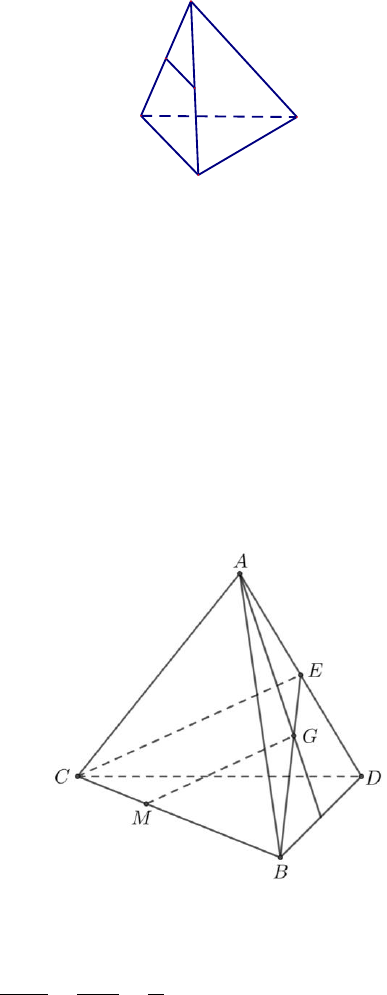
Bài 2. (1,0 điểm) Cho tứ diện
SABC
. Gọi
,,M N E
lần lượt là trung điểm của
AC
,
BC
,
SB
. Gọi
, HK
lần lượt là trọng tâm của các tam giác
SAC
và
SBC
.
a) Chứng minh
// .HK SAB
b) Chứng minh
HK
song song với giao tuyến của hai mặt phẳng
MNE
và
SAB
.
Bài 3. (1,0 điểm) Cáo Bắc Cực là loại động vật phổ biến ở vùng đồng hoang Bắc
Cực. Giả sử số lượng cáo ở Bắc Manitoba, Canada được biểu diễn theo hàm

500sin 1000
12
t
ft
trong đó
t
là thời gian, tính bằng tháng
1 12,tt
.
Hỏi vào thời điểm nào trong năm thì số lượng cáo đạt 1250 con?
-----HẾT-----

SỞ GIÁO DỤC & ĐÀO TẠO …
TRƯỜNG …
MÃ ĐỀ MT103
HƯỚNG DẪN GIẢI
KIỂM TRA GIỮA HỌC KÌ 1
MÔN: TOÁN – LỚP 11
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (7,0 điểm)
Bảng đáp án trắc nghiệm:
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
Câu
Đáp án
Câu 1
A
Câu 11
C
Câu 21
C
Câu 31
B
Câu 2
C
Câu 12
D
Câu 22
C
Câu 32
D
Câu 3
B
Câu 13
D
Câu 23
D
Câu 33
B
Câu 4
B
Câu 14
A
Câu 24
D
Câu 34
C
Câu 5
D
Câu 15
A
Câu 25
C
Câu 35
A
Câu 6
B
Câu 16
C
Câu 26
A
Câu 7
B
Câu 17
A
Câu 27
A
Câu 8
B
Câu 18
C
Câu 28
B
Câu 9
C
Câu 19
D
Câu 29
B
Câu 10
D
Câu 20
C
Câu 30
C
Hướng dẫn giải chi tiết
Câu 1.
Đáp án đúng là: A
Theo định nghĩa 1 rađian là số đo của cung có độ dài bằng bán kính.
Câu 2.
Đáp án đúng là: C
Từ đường tròn lượng giác ta có: góc lượng giác có số đo
o
135
là góc có tia đầu là
tia
OA
, tia cuối là tia
OP
và quay theo chiều âm (chiều kim đồng hồ).
Câu 3.
Đáp án đúng là: B
Góc lượng giác
có điểm cuối ở góc phần tư thứ II thì
sin 0,cos 0,tan 0,cot 0
Do đó
sin sin
;
2
sin sin sin
;
2
cos cos cos
.
Vậy ta chọn phương án B.
Câu 4.
Đáp án đúng là: B
Ta có:
2
cos 2 1 cos 2 cos cos
4 4 4 4 2
kk
.
Câu 5.
Đáp án đúng là: D
Do
1
cot
3
nên
sin 0
, ta chia cả tử và mẫu của
P
cho
sin
thì được
1
3 4.
3 4cot
3
13
1
2 5cot
2 5.
3
P
.
Câu 6.
Đáp án đúng là: B
Áp dụng công thức
cos cos sin sin cosx y x y x y
, ta được

cos cos sin sinM a b a b a b a b
2
cos cos2 1 2sina b a b a a
.
Câu 7.
Đáp án đúng là: B
Hàm số
cosyx
là hàm số chẵn. Do đó phương án B là sai.
Câu 8.
Đáp án đúng là: B
Hàm số
tanyx
tuần hoàn với chu kì
.
Câu 9.
Đáp án đúng là: C
Hàm số
tanyx
đồng biến trên mỗi khoảng
;
22
kk
với mọi
k
.
Câu 10.
Đáp án đúng là: D
Ta có
1 cos 1 3 cos 2 1,x x x R
.
Do đó không tồn tại căn bậc hai của
cos 2x
.
Vậy tập xác định
D
.
Câu 11.
Đáp án đúng là: C
Ta có
2 2 2 2 2 2
sin 2cos sin cos cos 1 cosy x x x x x x
Do
22
2
1 cos 1 0 cos 1 1 1 cos 2 .
1
M
x x x
m
Suy ra
2 2 2.1 4Mm
.
Câu 12.
Đáp án đúng là: D
oo
oo
o
oo
oo
2 60 360
60 360
cos2 cos 60
2 60 360
20 120
x x k
xk
xx
x x k
xk
với
k
.

Câu 13.
Đáp án đúng là: D
Công thức nghiệm
xk
với
k
là công thức nghiệm của phương trình
tan tanx
.
Câu 14.
Đáp án đúng là: A
sin 1 2 , 2 ,
4 4 2 4
x x k k x k k
Do
37
;2 2 2
4 8 8
x k k
kMà
kk
Vậy phương trình không có nghiệm trên đoạn
;2
.
Câu 15.
Đáp án đúng là: A
Ta có
5
cot 3 1 3 cot 3 1 cot cot
66
xx
5 1 5
3 1 ,
6 3 18 3
x k x k k
.
Câu 16.
Đáp án đúng là: C
Ta có
1
7 7.1u
,
2
14 7.2u
,
3
21 7.3u
,
4
28 7.4u
,… Suy ra
7
n
un
.
Câu 17.
Đáp án đúng là: A
Ta có
1
2
n
n
u
1
1
1
2
n
n
u
,
*n
.
Câu 18.
Đáp án đúng là: C

Ta có:
•
1 cos 2 1n
nên
n
u
bị chặn.
•
2 5 2 21
5 2 5 5 5 2
n
n
v
nn
khi đó
2 2 21
5 5 5 5.1 2
n
v
hay
2
1
5
n
v
nên
n
v
bị
chặn.
•
1 khi chan
1
1 khi le
n
n
n
nên ta luôn có
1 1 1
n
, do đó
n
a
bị chặn.
•
2
2
4 9 2 5 5n n n
nên dãy số
n
k
là dãy số bị chặn dưới nhưng khi
n
càng lớn thì
n
k
càng lớn nên dãy số
n
k
không bị chặn trên nên
n
k
không bị chặn.
Câu 19.
Đáp án đúng là: D
Phương án A: dãy số
1 3 5 7 9
;;;;
22222
là cấp số cộng với
1
1
;1
2
ud
.
Phương án B: dãy số
1;1;1;1;1
là cấp số cộng với
1
1; 0ud
.
Phương án C: dãy số
8; 6; 4; ;2;0
là cấp số cộng với
1
8; 2ud
.
Phương án D: dãy số
3;1; 1; 2; 4
không là cấp số cộng vì
21
2uu
và
43
1uu
.
Câu 20.
Đáp án đúng là: C
Ta có
1
13 1
5
13 1 5 3 13 1 31
3
u
u u d
d
.
Câu 21.
Đáp án đúng là: C
Giá của chiếc xe sau
n
năm là:
700 50 1
n
un
Vậy sau 5 năm sử dụng giá của chiếc xe là:
5
700 50. 5 1 500u
(triệu đồng).
Câu 22.
Đáp án đúng là: C
Vì
O AC SAC
nên
O SAC
.
Vì
O AC ABCD
nên
O ABCD
.
Vì
O BD SBD
nên
O SBD
.
Câu 23.
Đáp án đúng là: D
Ta có:
BC ABC
BC ABC BCD
BC BCD
Vậy giao tuyến của mặt phẳng
ABC
và mặt phẳng
BCD
là đường thẳng
BC
.
Câu 24.
Đáp án đúng là: D
Hình chóp có đáy là ngũ giác có:
•
6
mặt gồm
5
mặt bên và
1
mặt đáy.
•
10
cạnh gồm
5
cạnh bên và
5
cạnh đáy.
Câu 25.
Đáp án đúng là: C
Cả 3 hình đều là hình biểu diễn của hình tứ diện.
Câu 26.
Đáp án đúng là: A

Dễ thấy
NG
và
AM
cùng nằm trong mặt phẳng
AMD
.
Mặt khác ta lại có
1
2
DN
DA
,
2
3
DG
DM
.
Do đó
NG
và
AM
cắt nhau.
Gọi
I NG AM
,
AM ABC
I NG ABC
.
Vậy khẳng định đúng là
I AM
.
Câu 27.
Đáp án đúng là: A
S
là điểm chung thứ nhất giữa hai mặt phẳng
MSB
và
.SAC
Ta có
I BM SBM I SBM
I AC SAC I SAC
I
là điểm chung thứ hai giữa hai mặt phẳng
MSB
và
.SAC
I
G
N
M
D
C
B
A
I
M
A
D
B
C
S

Vậy
.MSB SAC SI
Câu 28.
Đáp án đúng là: B
Đường thẳng
c
cắt
a
thì
c
cắt
b
hoặc
c
và
b
chéo nhau.
Câu 29.
Đáp án đúng là: B
//AB CD
,
AC
cắt
BD
,
SB
và
CD
chéo nhau,
SD
và
BC
chéo nhau.
Câu 30.
Đáp án đúng là: C
Câu 31.
Đáp án đúng là: B
Ta có:
//
//
MN MCD SAB
AB SAB
MN CD
CD MCD
AB CD
.
Câu 32.
Đáp án đúng là: D
Vì
//ab
nên mọi mặt phẳng
chứa
a
và không chứa
b
đều song song với
b
.
Câu 33.
Đáp án đúng là: B
Mệnh đề B sai vì
b
và
d
có thể chéo nhau.
Câu 34.
Đáp án đúng là: C
Ta có
M
,
N
lần lượt là trung điểm của
AB
,
AC
MN
là đường trung bình của tam giác
ABC
//MN BC
.
Ta có
// ,
//
MN BC BC BCD
MN BCD
MN BCD
.
Câu 35.
Đáp án đúng là: A
Gọi
E
là trung điểm của
AD
.
Xét tam giác
BCE
có,
2
3
BM BG
BC BE
. Suy ra
//MG CE
.
N
M
B
D
C
A

Vì
CE ACD
và
MG ACD
nên
//MG ACD
.
PHẦN II. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm)
a)
cos 3 sin 3 3 *
63
xx
Ta thấy
33
6 3 2
xx
nên
sin 3 cos 3
36
xx
Do đó
* 2cos 3 3
6
x
3
cos 3
62
x
32
66
32
66
xk
k
xk
2
3
2
93
k
x
k
k
x
Vậy phương trình có nghiệm là
22
;
3 9 3
kk
x x k
.
b)
sin sin2 sin3 0x x x
2sin2 .cos sin2 0x x x
sin2 2cos 1 0xx
2
sin2 0
2
1
2
cos
3
2
xk
x
k
xk
x
2
2
2
3
k
x
k
xk

Vậy phương trình có nghiệm là
2
;2
23
k
x x k k
.
Bài 2. (1,0 điểm)
a) Tam giác
SAC
có
H
là trọng tâm nên
2
3
SH
SM
.
Tương tự, ta được
2
3
SK
SN
.
Do đó
2
3
SH SK
SM SN
//HK MN
(định lí Thalèsđảo)
Mà
MN SAB
// HK SAB
1
b) Tam giác
ABC
có
, MN
lần lượt là trung điểm của
AC
và
BC
.
MN
vlà đường trung bình của tam giác
// .MN AB
Ta có
,MNE SABEE
Mà
//MN AB
;
MN MNE
và
AB SAB
Suy ra giao tuyến của
MNE
và
SAB
là đường thẳng
d
đi qua
E
và
// //d MN AB
Trong
SAB
: gọi
F d SA
Ta có
// ,HK MN MN MNEF
// 2HK MNEF
Mà
SAB MNEF EF
3
d
K
H
E
F
N
M
A
B
C
S
Từ (1), (2), (3), ta thu được
// .HK EF
Bài 3. (1,0 điểm)
Yêu cầu bài toán
500sin 1000 1250
12
t
1
sin
12 2
t
2
12 6
2
12 6
t
k
k
t
k
2 24
10 24
tk
k
tk
Do
1 12,tt
nên
2
10
t
t
.
Vậy vào thời điểm tháng 2 hoặc tháng 10 thì số lượng loài cáo đạt 1250 con.
-----HẾT-----