Giáo án Dấu của tam thức bậc 2 Toán 10 Chân trời sáng tạo

Ngày soạn: .../.../... Ngày dạy: .../.../...
CHƯƠNG VII. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
BÀI 1: DẤU CỦA TAM THỨC BẬC HAI
THỜI GIAN THỰC HIỆN: 3 TIẾT I. MỤC TIÊU:
1. Kiến thức: Học xong bài này, HS đạt các yêu cầu sau:
- Nhận biết được tam thức bậc hai.
- Tính được nghiệm và biệt thức của tam thức bậc hai.
- Xét được dấu của tam thức bậc hai.
- Áp dụng việc xét dấu tam thức bậc hai để giải quyết một số bài toán thực tế 2. Năng lực Năng lực chung:
- Năng lực tự chủ và tự học thông qua hoạt động cá nhân;
- Năng lực giao tiếp và hợp tác thông qua trao đổi với bạn bè và hoạt động nhóm;
- Năng lực giải quyết vấn đề. Năng lực riêng:
- Năng lực tư duy và lập luận toán học, mô hình hóa toán học.
- Năng lực vận dụng được dấu của tam thức bậc hai một ẩn vào giải quyết bài toán thực tiễn. 3. Phẩm chất


- Bổi dưỡng hứng thú học tập, ý thức làm việc nhóm, ý thức tìm tòi, khám phá và sáng tạo cho HS.
- Rèn luyện tính cần thận, chính xác. Tư duy các vấn đề toán học một cách lôgic và hệ thống.
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần
trách nhiệm hợp tác xây dựng cao.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU 1 - GV:
- SGK, tài liệu giảng dạy, kế hoạch bài dạy, máy chiếu.
- Nghiên cứu kĩ bài học và phương pháp dạy học phù hợp.
- Sưu tầm các hình ảnh thực tế, video minh họa liên quan đến bài học, các thiết bị
dạy học phục vụ hình thành và phát triển năng lực HS.
2 - HS: SGK, SBT, vở ghi, giấy nháp, đồ dùng học tập (bút, thước...), bảng nhóm, bút viết bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
A. HOẠT ĐỘNG KHỞI ĐỘNG (MỞ ĐẦU) a) Mục tiêu:
- Tạo sự tò mò và hứng thú cho HS thông qua hình ảnh quen thuộc trong cuộc sống là cây cầu vòm
→ Nhu cầu xét dấu hàm số bậc hai
b) Nội dung: GV cho học sinh quan sát một số hình ảnh thực tế cây cầu vòm, sau
đó cho HS xem hình ảnh trong SGK và đặt câu hỏi cho HS trả lời.
c) Sản phẩm: HS trả lời câu hỏi mở đầu theo suy nghĩ của mình (có thể đúng hoặc
sai), bước đầu hình dung về dấu của tam thức bậc hai.


d) Tổ chức thực hiện:
Bước 1: Chuyển giao nhiệm vụ:
- GV dẫn dắt, yêu cầu HS đọc tình huống mở đầu và dự đoán:
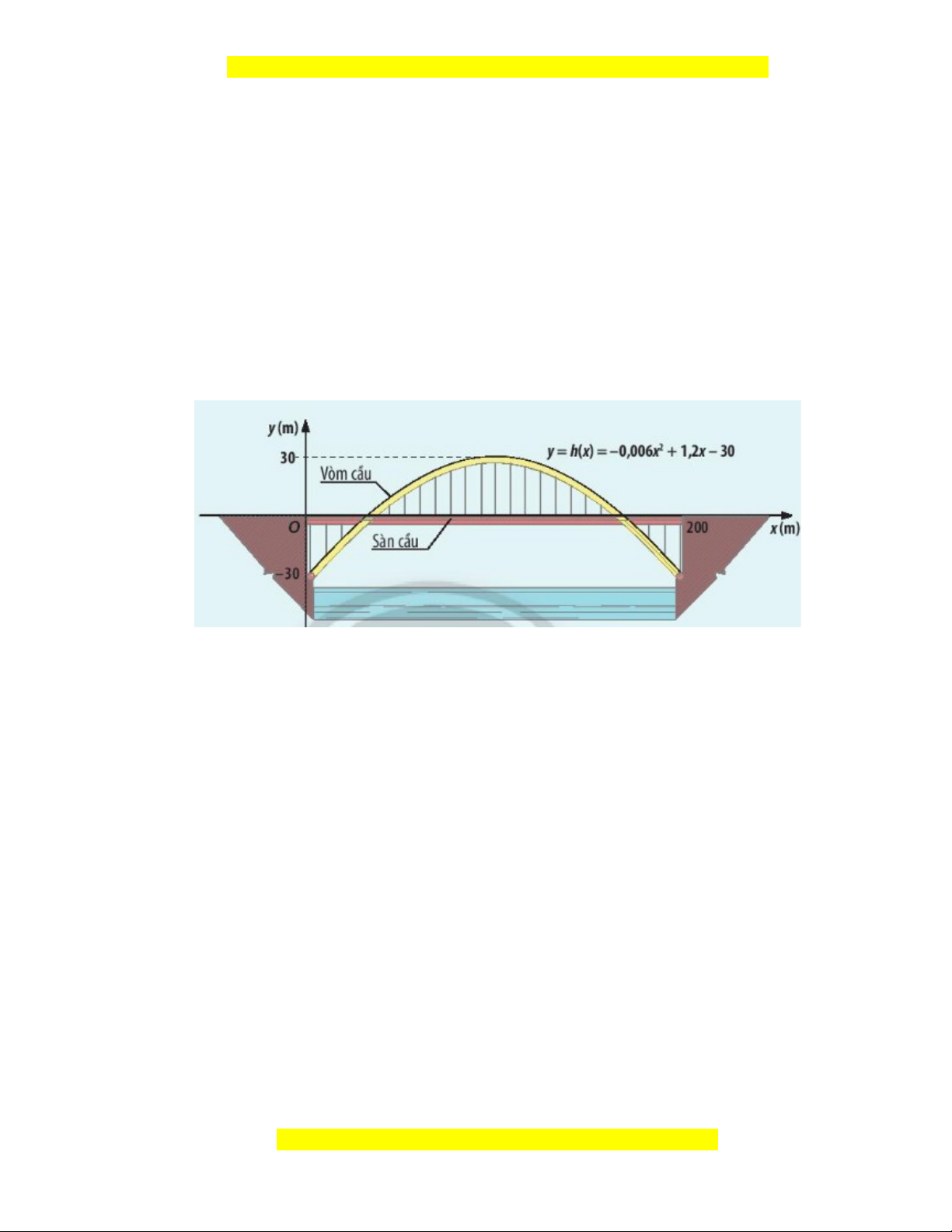
+ “Cầu vòm được thiết kế với thanh vòm hình parabol và mặt cầu đi ở giữa. Trong
hệ trục tọa độ Oxy như hình vẽ, phương trình của vòm cầu là y = h(x) = -0,006x2
+ 1,2x – 30. Với giá trị h(x) như thế nào tại vị trí x (0≤ x ≤ 200), vòm cầu: cao hơn
mặt cầu, thấp hơn mặt cầu?”
Bước 2: Thực hiện nhiệm vụ: HS quan sát và chú ý lắng nghe, thảo luận nhóm
đôi trả lời nhanh kết quả và giải thích.
Bước 3: Báo cáo, thảo luận: GV gọi một số HS trả lời, HS khác nhận xét, bổ sung.
Bước 4: Kết luận, nhận định: GV đánh giá kết quả của HS, trên cơ sở đó dẫn dắt
HS vào bài học mới: "Đa thức bậc hai f(x) = ax2 + bx + c (a≠0) còn gọi là tam thức
bậc hai. Để xét dấu của biểu thức dạng f(x) = ax2 + bx + c ta có cách nào? Sau
đây, ta sẽ làm quen với việc xét dấu của tam thức bậc hai".
 Bài 1: Dấu của tam thức bậc hai.
B. HÌNH THÀNH KIẾN THỨC MỚI


Hoạt động 1: Tam thức bậc hai a) Mục tiêu:
- HS ghi nhớ khái niệm tam thức bậc hai và nhận biết được tam thức bậc hai.
- Nhận biết khái niệm và xét được dấu của tam thức bậc hai dựa vào định nghĩa.
- Tính được nghiệm và biệt thức của tam thức bậc hai. b) Nội dung:
- Giáo viên đưa ra lần lượt các câu hỏi, hình ảnh các dạng đồ thị của hàm số bậc hai.
- HS quan sát SGK để tìm hiểu nội dung kiến thức theo yêu cầu của GV để hình
thành và tiếp nhận kiến thức liên quan đến tam thức bậc hai.
c) Sản phẩm: HS ghi nhớ được khái niệm hàm số, tập xác định, tập giá trị của hàm
số và hoàn thành được các bài tập Ví dụ 1, Thực hành 1, Thực hành 2.
d) Tổ chức thực hiện: HĐ CỦA GV VÀ HS
SẢN PHẨM DỰ KIẾN
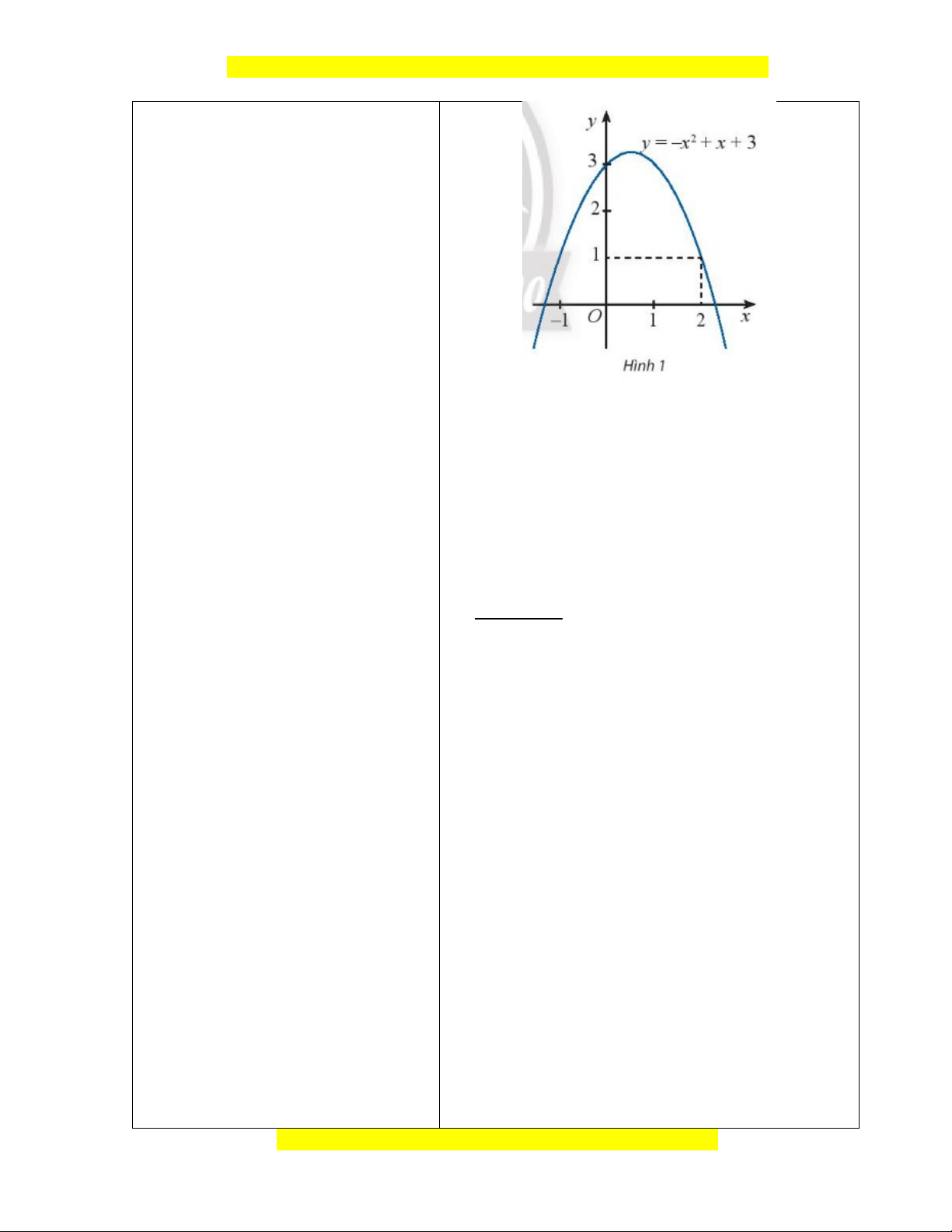
Bước 1: Chuyển giao nhiệm 1. Tam thức bậc hai vụ: HĐKP1.
- GV tổ chức cho HS hoạt động
nhóm đôi thực hiện HĐKP1.
+ HS nhắc lại khái niệm bậc của
đa thức và cách tính giá trị của
đa thức (thực hiện bằng cách
thay trực tiếp giá trị của x vào công thức).