CHƯƠNG VII. CHƯƠNG I
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG TOÁN HÌNH HỌC ➉
PHƯƠNG TRÌNH ĐƯỜNG TRÒN 21
TRONG MẶT PHẲNG TỌA ĐỘ 1
PHƯƠNG TRÌNH ĐƯỜNG TRÒN 1 2
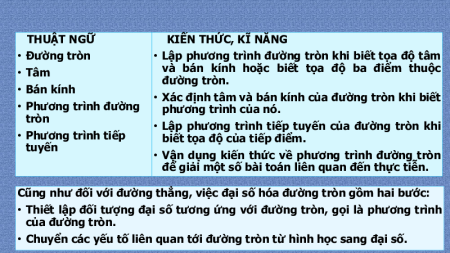
PHƯƠNG TRÌNH TIẾP TUYẾN 2 2 3 4 5 THUẬT NGỮ
KIẾN THỨC, KĨ NĂNG • Đường tròn • Lập
phương trình đường tròn khi biết tọa độ tâm • Tâm
và bán kính hoặc biết tọa độ ba điểm thuộc đường tròn. • Bán kính
• Xác định tâm và bán kính của đường tròn khi biết
• Phương trình đường
phương trình của nó. tròn
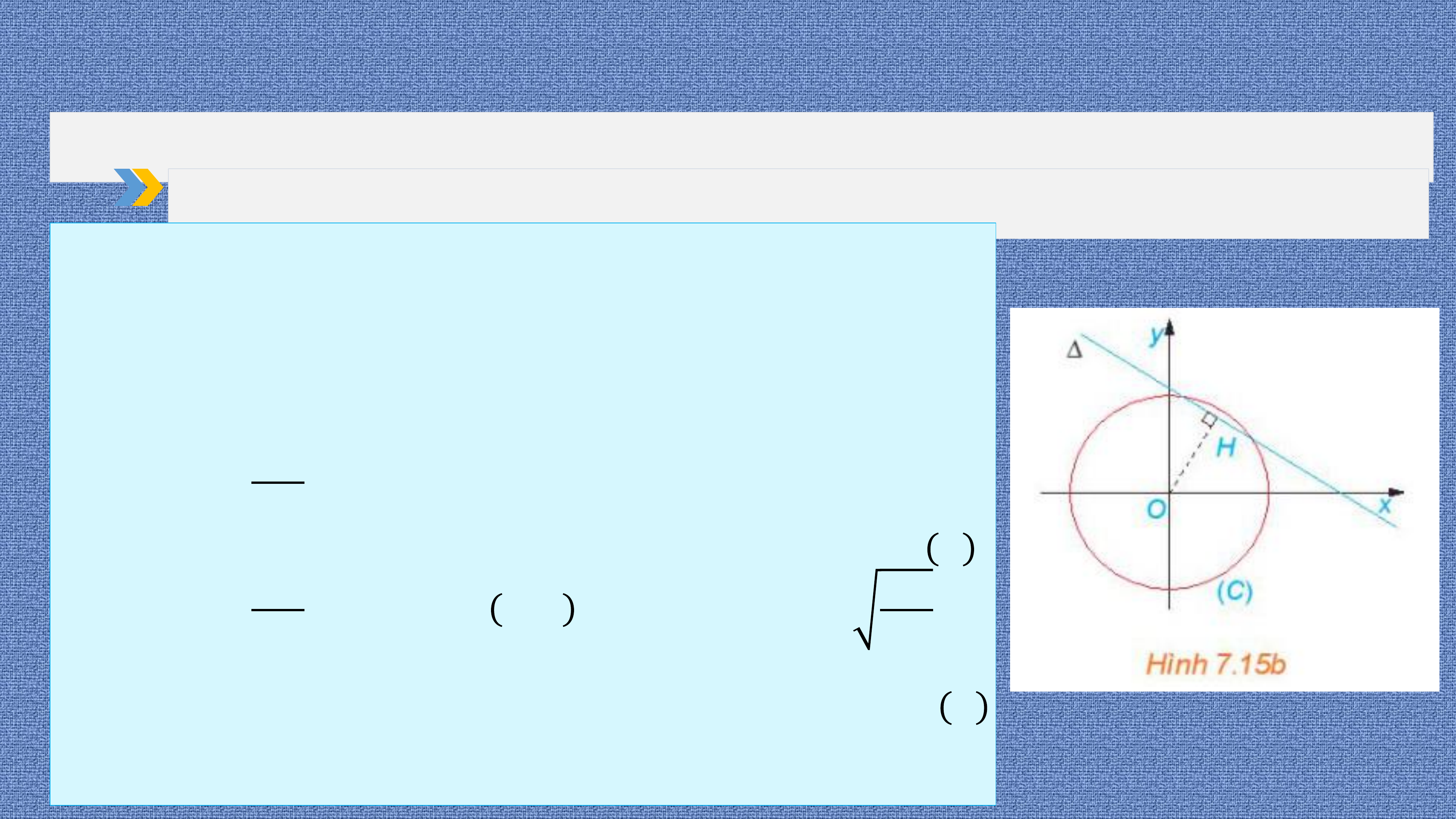
• Lập phương trình tiếp tuyến của đường tròn khi
• Phương trình tiếp
biết tọa độ của tiếp điểm. tuyến
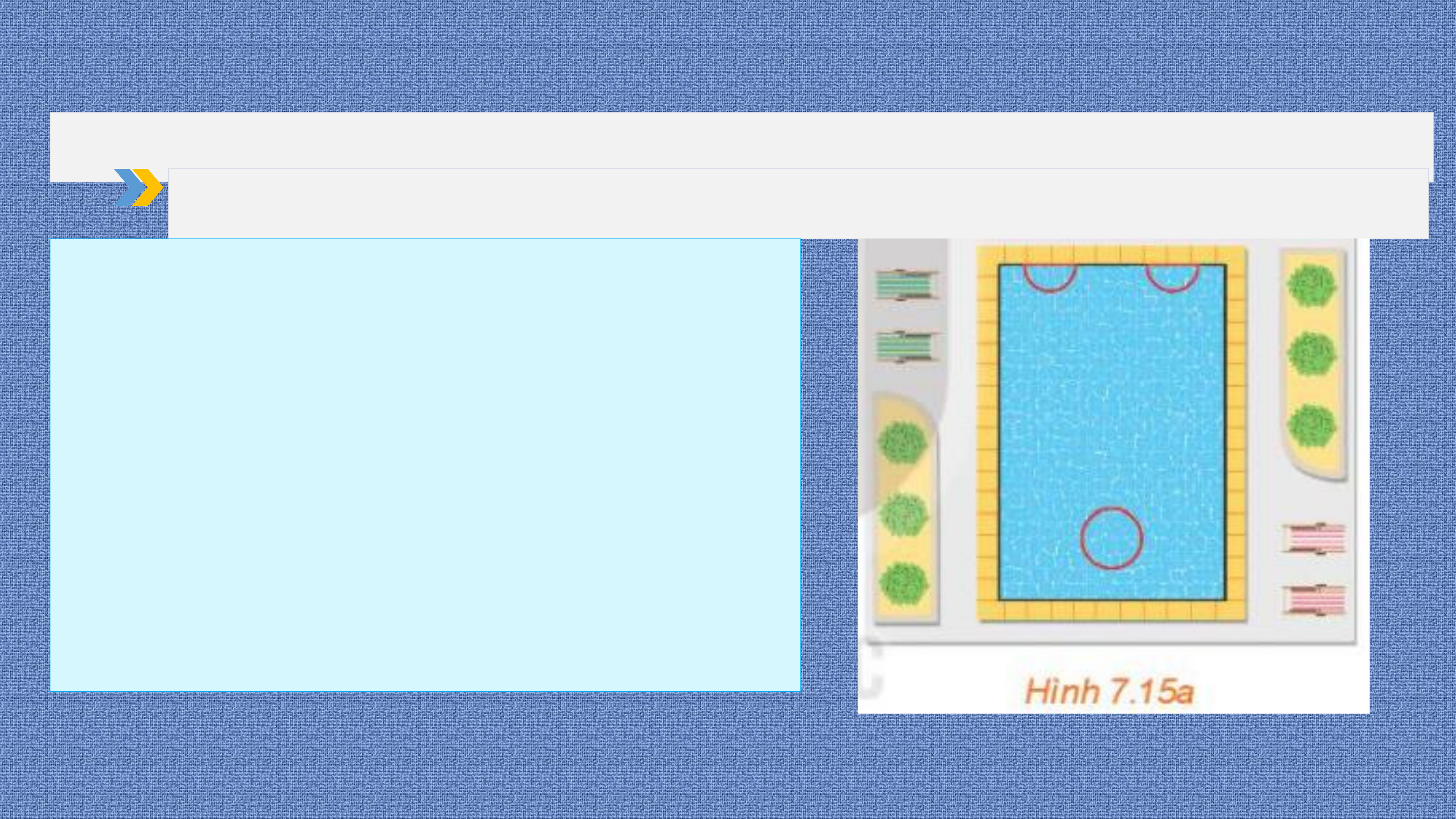
• Vận dụng kiến thức về phương trình đường tròn
để giải một số bài toán liên quan đến thực tiễn.
Cũng như đối với đường thẳng, việc đại số hóa đường tròn gồm hai bước:
• Thiết lập đối tượng đại số tương ứng với đường tròn, gọi là phương trình của đường tròn.
• Chuyển các yếu tố liên quan tới đường tròn từ hình học sang đại số.
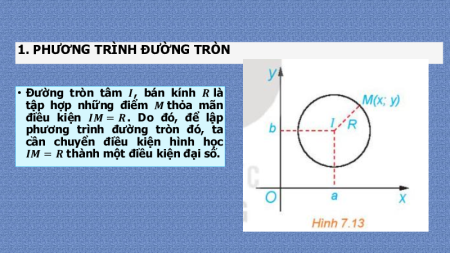
1. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
• Đường tròn tâm ?, bán kính ? là
tập hợp những điểm ? thỏa mãn
điều kiện ?? = ? . Do đó, để lập
phương trình đường tròn đó, ta
cần chuyển điều kiện hình học
?? = ? thành một điều kiện đại số.
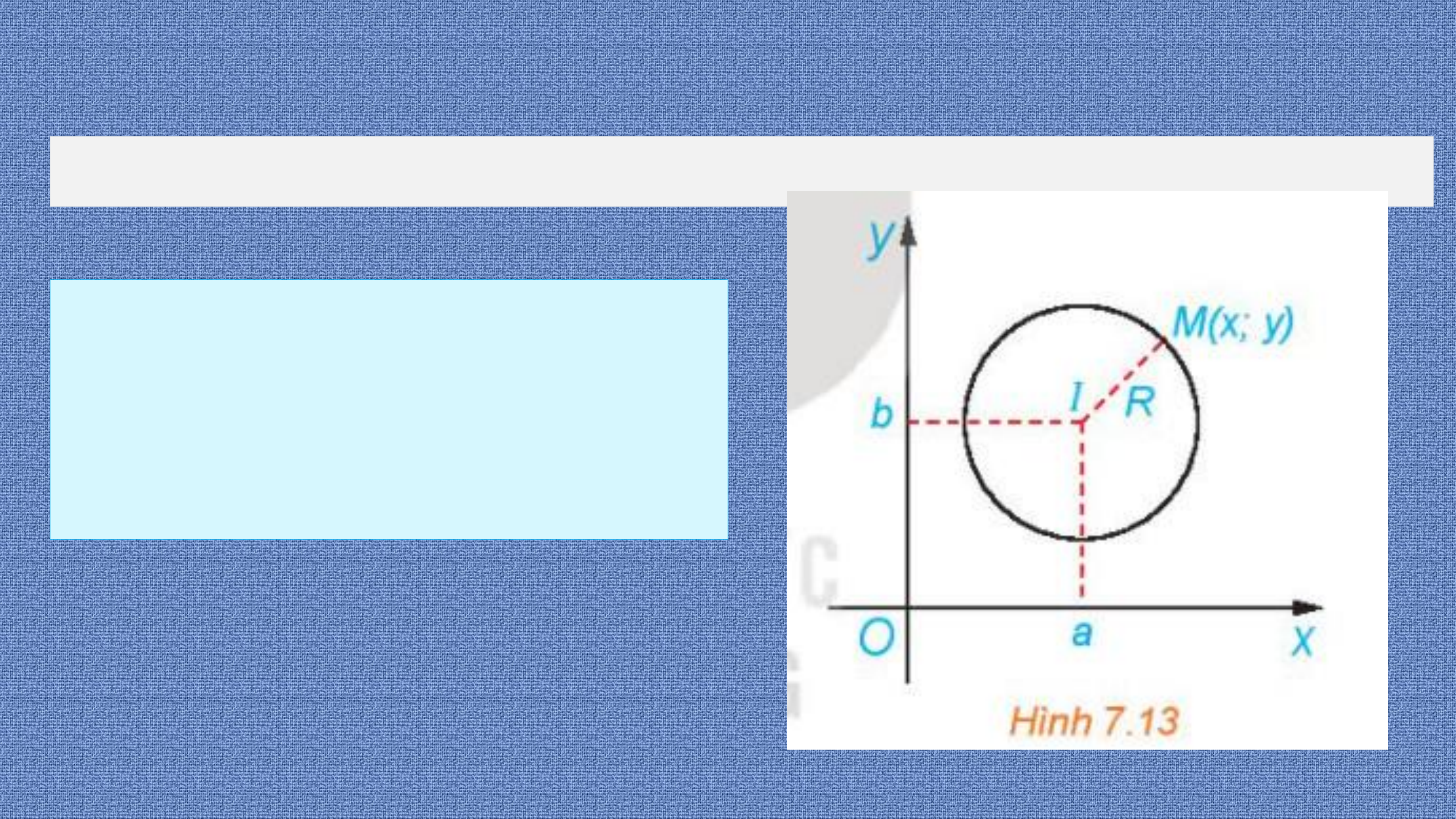
1. PHƯƠNG TRÌNH ĐƯỜNG TRÒN HĐ1
Trong mặt phẳng tọa độ Oxy, cho Hướng dẫn
đường tròn (?), tâm ?(?; ?), bán kính
? ?; ? ∈ ? ⇔ ?? = ?
? (H.7.13).Khi đó, một điểm ?(?; ?) ⇔
? − ? ? + ? − ? ? = ?
thuộc đường tròn (?) khi và chỉ tọa độ
⇔ ? − ? ? + ? − ? ? = ??.
của nó thỏa mãn điều kiện đại số nào?
• Điểm ? ?; ? thuộc đường tròn ? , tâm ? ?; ? , bán kính ? khi và chỉ khi
? − ? ? + ? − ? ? = ?? ?
• Ta gọi ? là phương trình của đường tròn (C).
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16