Bài giảng Powerpoint Toán 10 học kì 2 Kết nối tri thức

388 194 lượt tải
Chia sẻ Facebook Báo cáo tài liệu
Lớp: Lớp 10
Môn: Toán Học
Bộ sách: Kết nối tri thức với cuộc sống
Dạng: Giáo án, Giáo án Powerpoint
File:
Loại: Bộ tài liệu bao gồm: 20 TL lẻ ( Xem chi tiết » )

CÁCH MUA:

Liên hệ ngay Hotline hỗ trợ: 0842834585

Bộ bài giảng điện tử Toán 10 Kết nối tri thức được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024.  

Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!

  • Bộ bài giảng powerpoint Toán 10 Kết nối tri thức bao gồm đầy đủ các bài giảng cả năm. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán 10 bộ Kết nối tri thức.
  • Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.

Đánh giá

4.6 / 5(388 )
5
53%
4
22%
3
14%
2
5%
1
7%
Trọng Bình
Tài liệu hay

Giúp ích cho tôi rất nhiều

Duy Trần
Tài liệu chuẩn

Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)

TÀI LIỆU BỘ BÁN CHẠY

Xem thêm

Tài liệu bộ mới nhất

TẢI NGAY
Lớp 10 Hóa Học

3 đề thi Hóa học 10 Cuối kì 2 Chân trời sáng tạo cấu trúc mới

Word

100.000 ₫
27 7 13
TẢI NGAY
Lớp 10 Hóa Học

3 đề thi Hóa học 10 Cuối kì 2 Cánh diều cấu trúc mới

Word

100.000 ₫
28 4 8
TẢI NGAY
Lớp 10 Hóa Học

3 đề thi Hóa học 10 Cuối kì 2 Kết nối tri thức cấu trúc mới

Word

100.000 ₫
26 4 8
TẢI NGAY
Lớp 10 Toán Học

5 đề thi Toán 10 Cuối kì 2 Chân trời sáng tạo cấu trúc mới


150.000 ₫
44 88
TẢI NGAY
Lớp 10 Toán Học

5 đề thi Toán 10 Cuối kì 2 Kết nối tri thức cấu trúc mới


150.000 ₫
53 106
TẢI NGAY
Lớp 10 Toán Học

5 đề thi Toán 10 Cuối kì 2 Cánh diều cấu trúc mới


150.000 ₫
41 82
TẢI NGAY
Lớp 10 Toán Học

Bộ 7 đề thi cuối kì 2 Toán 10 TP Hồ Chí Minh có đáp án


100.000 ₫
58 116
TẢI NGAY
Lớp 10 Toán Học

Bộ 6 đề thi cuối kì 1 Toán 10 Hà Nội có đáp án


100.000 ₫
51 101
TẢI NGAY
Lớp 9 Toán Học

Bộ đề thi giữa kì 1 Toán 9 Kết nối tri thức có đáp án


Miễn phí
60
TẢI NGAY
Lớp 9 Toán Học

Bộ đề thi giữa kì 1 Toán 9 Cánh diều có đáp án


Miễn phí
49
CHƯƠNG I
§15. Hàm số
§16. Hàm số bậc hai
§17. Dấu của tam thức bậc hai
§18. Phương trình quy về phương
trình bậc nhất bậc hai
CHƯƠNG VI. HÀM SỐ - ĐỒ THỊ VÀ ỨNG DỤNG
CHƯƠNG I
CHƯƠNG VI. HÀM SỐ - ĐỒ THỊ VÀ ỨNG DỤNG
1
ĐỒ THỊ CỦA HÀM SỐ
2
4
1
2
3
TOÁN ĐẠI SỐ
➉
1
KHÁI NIỆM HÀM SỐ
HÀM SỐ
15
SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
3
BÀI TẬP
4
1. KHÁI NIỆM HÀM SỐ
Hướng dẫn:
• Tại thời điểm 8 giờ nồng độ bụi là 57,9.
• Tại thời điểm 12 giờ nồng độ bụi là 69,07.
• Tại thời điểm 16 giờ nồng độ bụi là 81,78.
• Mỗi thời điểm tương ứng với một giá trị
nồng độ bụi PM 2.5
HĐ1:Bảng  cho biết nồng độ bụi PM  trong không khí theo thời gian trong
ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội:
Bảng
6.1
(Theo moitruongthudo. vn)
•Hãy cho biết nồng độ bụi PM
2.5
tại mỗi thời
điểm 8 giờ, 12 giờ, 16 giờ.
•Trong Bảng
6.1
, mỗi thời điểm tương ứng với
bao nhiêu giá trị của nồng độ bụi PM
2.5
?
Thời điểm (giờ)
0 4 8 12 16
Nồng độ bụi PM
 
74,27
64,58 57,9 69,07 81,78
Quan sát Hình 6.1.
a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến
năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất,
thấp nhất?
Giải
Thời gian theo dõi mực nước biển ở Trường Sa được thể
hiện trong hình từ năm 2013 đến năm 2019.
Trong khoảng thời gian đó, năm 2013 và 2018 mực nước
biển trung bình tại Trường Sa cao nhất, năm 2015 thấp nhất.
HĐ2:
1. KHÁI NIỆM HÀM SỐ
Tính tiền điện.
a) Dựa vào Bảng  về giá bán lẻ điện sinh hoạt, hãy
tính số tiền phải trả ứng với mỗi lượng điện tiêu
thụ ở Bảng 6.3:
b) Gọi x là lượng điện tiêu thụ (đơn vị KWh) và là số
tiền phải trả tương ứng (đơn vị nghìn đồng). Hãy
viết công thức mô tả sự phụ thuộc của vào khi
.
1. KHÁI NIỆM HÀM SỐ
HĐ3:
󰇜 khi .
Trong HĐ, nếu gọi là thời điểm và là nồng độ bụi
PM thì với mỗi giá trị của , xác định được chỉ một
giá trị tương ứng của . Ta tìm thấy mối quan hệ phụ
thuộc tương tự giữa các đại lượng trong HĐ, HĐ3.
1. KHÁI NIỆM HÀM SỐ
HĐ3:
Lượng điện tiêu thụ (kWh)
50 100 200
Số tiền (nghìn đồng)
83900 173400
402800
1. KHÁI NIỆM HÀM SỐ
Nếu
với mỗi giá trị của thuộc tập hợp số có một và chỉ một giá trị
tương
ứng của thuộc tập số thực thì ta có một hàm số.
Ta
gọi là biến số và là hàm số của .
Tập
hợp gọi là tập xác định của hàm số.
Tập
tất cả các giá trị nhận được, gọi là tập giá trị của hàm số.
Khi
là hàm số của , ta có thể viết
• Trong HĐ1, nếu gọi là thời điểm, là nồng độ
bụi PM thì là biến số và là hàm số của .
Đó là hàm số được cho bằng bảng.
• Tập xác định của hàm số là  .
• Tập giá trị của hàm số là
 .
Ví dụ 1.
1. KHÁI NIỆM HÀM SỐ
Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vào thời gian của
một vật chuyển động thẳng đều với vận tốc . Tìm tập xác định của hàm
số đó. Tính quãng đường vật đi được sau 
Giải
• Một vật chuyển động thẳng đều với vận tốc m thì quâng đường đi
được (mét) phụ thuộc vào thời gian (giây) theo công thức ,
trong đó là biến số, là hàm số của . Tập xác định của hàm số là
󰇜

• Quãng đường vật đi được sau  là:
  .
• Quãng đường vật đi được sau  là:
  m .
Ví dụ 2.
Chú ý: Khi cho hàm số bằng công thức mà không chỉ rõ tập xác định của nó thì ta quy
ước tập xác định của hàm số là tập hợp tất cả các số thực sao cho biểu thức có nghĩa.
1. KHÁI NIỆM HÀM SỐ
Tìm tập xác định của các hàm số sau:
a)  ; b)

.
Giải
a) Biểu thức  có nghĩa khi  , tức là khi .
Vậy tập xác định của hàm số đã cho là
󰇜
󰇟 .
b) Biểu thức

có nghĩa khi , tức là khi .
Vậy tập xác định của hàm số đã cho là  .
Ví dụ 3.
1. KHÁI NIỆM HÀM SỐ
a) Hãy cho biết Bảng  có cho ta một hàm số hay không. Nếu có, tìm tập xác định và tập giá trị của
hàm số đó.
b) Trở lại HĐ2, ta có hàm số cho bằng biểu đồ. Hãy cho biết giá trị của hàm số tại .
Tìm tập xác định, tập giá trị của hàm số đó.
c) Cho hàm số 
. Tính ; và tìm tập xác định, tập giá trị của hàm số này.
Luyện tập 1.
1. KHÁI NIỆM HÀM SỐ
• Bảng 6.4 cho ta một hàm số.
• TXD  .
• Tập giá trị là  .
• Giá trị hàm số tại là 
• 
, 
.
• Tập xác định , Tập giá trị là .
Nhận xét: Một hàm số có thể được cho bằng bảng, bằng biểu đồ, bằng công thức hoặc bằng mô tả.
2. ĐỒ THỊ HÀM SỐ
HĐ4:
Quan sát Hình  và cho biết những điểm nào sau
đây nằm trên đồ thị của hàm số
:
    
Nêu nhận xét về mối quan hệ giữa hoành độ và tung
độ của những điểm nằm trên đồ thị.
Giải:
Điểm nằm trên đồ thị của hàm số là
:    .
Nhận xét: Giá trị hàm số tại hoành độ chính là tung
độ của điểm đó.
Đồ thị của hàm số xác định trên tập là tập hợp tất cả các điểm 
trên mặt phẳng toạ độ với mọi thuộc .
2. ĐỒ THỊ HÀM SỐ
2. ĐỒ THỊ HÀM SỐ
Viết công thức của hàm số cho ở HĐ3b. Tìm tập xác
định, tập giá trị và vẽ đồ thị của hàm số này.
Ví dụ 4.
Giải
Công thức của hàm số cho ở HĐ3b là  với
.
Tập xác định của hàm số này là  .
Vì  nên  .
Vậy tập giá trị của hàm số là  .
Đồ thị của hàm số  trên  là một đoạn
thẳng
2. ĐỒ THỊ HÀM SỐ
a) Dựa vào đồ thị của hàm số
 , tìm
sao cho .
b) Vẽ đồ thị của các hàm số  và 
trên cùng một mặt phẳng toạ độ.
Luyện tập 2
Giải
a) Dựa vào đồ thị của hàm số ta thấy ứng với
.
2. ĐỒ THỊ HÀM SỐ
a) Dựa vào đồ thị của hàm số
 , tìm
sao cho .
b) Vẽ đồ thị của các hàm số  và 
trên cùng một mặt phẳng toạ độ.
Luyện tập 2
2. ĐỒ THỊ HÀM SỐ
Nếu lượng điện tiêu thụ từ trên 50 đến kWh󰇛󰇜 thì công thức
liên hệ giữa và đã thiết lập ở HĐ3 không còn đúng nữa.
Theo bảng giá bán lẻ điện sinh hoạt (Bảng 6.2) thì số tiền phải trả là:
      
hay   󰇛nghìn đồng󰇜.
Vậy trên tập xác định 󰇟󰇠, hàm số mô tả số tiền phải thanh toán có
công thức là  ; tập giá trị của nó là .
Hãy vẽ đồ thị ở Hình  vào vở rồi vẽ tiếp đồ thị của hàm số 
trên tập  .
Vận dụng 1
2. ĐỒ THỊ HÀM SỐ
Hàm số mô tả sự phụ thuộc của (số tiền phải trả vào )
(lượng điện tiêu thụ ) trên từng khoảng giá trị được
cho bằng công thức như sau:
 nếu 
  nếu 
 nếu 
  nếu 
  nêu 
Đồ thị của hàm số trên được vẽ như hình 6.4.
Tìm hiểu thêm
CHƯƠNG I
§15. Hàm số
§16. Hàm số bậc hai
§17. Dấu của tam thức bậc hai
§18. Phương trình quy về
phương trình bậc hai
CHƯƠNG VI. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
CHƯƠNG I
CHƯƠNG VI. HÀM SỐ, ĐỒ THỊ VÀ ỨNG DỤNG
SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
3
BÀI TẬP
4
1
5
TOÁN ĐẠI SỐ
➉
HÀM SỐ
15
4
3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Cho hàm số  và . Tính giá trị theo giá trị để
hoàn thành bảng sau:
Hoạt động 5
x
2−
1−
2
1yx= − +
?
?
?
?
?
yx=
?
?
?
?
?
Khi giá trị tăng thì giá trị của của mỗi hàm số  và
tăng hay giảm
x
2−
1−
1yx= − +
?????
yx=
?????
3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Hoạt động 5
x
2−
1−
0
1
2
1yx= − +
3
2
1
0
1−
yx=
2−
1−
0
1
2
Khi giá trị tăng thì giá trị của của hàm số  tăng còn giá
trị của hàm số giảm.
3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Quan sát đồ thị của hàm số 
trên .
Hỏi:
a, Giá trị của tăng hay giảm
khi tăng trên khoảng  ?
b, Giá trị của tăng hay giảm
khi tăng trên khoảng  ?
Hoạt động 6
• Hàm số 󰇛󰇜 được gọi là đồng biến trên khoảng 󰇛󰇜 nếu


󰇛
󰇜
• Hàm số 󰇛󰇜 được gọi là đồng biến trên khoảng 󰇛󰇜 nếu


󰇛
󰇜
3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
( )
y f x=
( )
;ab
( ) ( ) ( )
1 2 1 2 1 2
, ; , .x x a b x x f x f x
( )
y f x=
( )
;ab
( ) ( ) ( )
1 2 1 2 1 2
, ; , .fx x a b x x x f x 
Ví dụ 5.
Hàm số
đồng biến hay nghịch biến
trên mỗi khoảng  và  ?
• Trên khoảng 󰇛󰇜, đồ thị “đi xuống" từ trái sang phải và
với

thì
󰇛
󰇜. Như vậy,
hàm số
nghịch biến trên khoảng 󰇛󰇜.
• Trên khoảng 󰇛󰇜, đồ thị "đi lên" từ trái sang phải và
với

thì
󰇛
󰇜. Như vậy,
hàm số
đồng biến trên khoảng 󰇛󰇜.
Chú ý
•
Đồ thị của một hàm số đồng biến trên khoảng
󰇛󰇜
là đường
"đi lên" từ trái sang phải;
•
Đồ thị của một hàm số nghịch biến trên khoảng
󰇛󰇜
là đường
"đi xuống" từ trái sang phải.
3. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Luyện tập 3.
Vẽ đồ thị của hàm số  và 
. Hãy cho biết
a) Hàm số  đồng biến hay nghịch biến trên .
b) Hàm số 
đồng biến hay nghịch biến trên mỗi khoảng:
󰇛󰇜 và 󰇛󰇜.
Luyện tập 3.
Vẽ đồ thị của hàm số .
a) Hàm số  đồng biến hay nghịch biến trên .
Hàm số  đồng biến trên .
Luyện tập 3.
Vẽ đồ thị của hàm số 
.
b) Hàm số 
đồng biến hay
nghịch biến trên mỗi khoảng: 󰇛󰇜 và
󰇛󰇜.
Hàm số 
đồng biến trên 󰇛󰇜
và nghịch biến trên 󰇛󰇜.
Vận dụng 2.
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7
a, Tính số tiền phải trả khi di
chuyển 25 km.
b, Lập công thức tính số tiền
cước taxi phải trả theo kilomet
số di chuyển.
c, Vẽ đồ thị và cho biết hàm số
đồng biến trên khoảng nào,
nghịch biến trên khoảng nào.
Vận dụng 2.
a, Số tiền phải trả khi di chuyển 25 km là
  
(nghìn đồng)
Vận dụng 2.
b, Lập công thức tính số tiền cước taxi phải trả theo kilomet số di chuyển.
( )
( ) ( )
10000 0 0,6
10000 13000 -0,6 0,6 24
10000 13000 24-0,6 11000 -24 24
khi x
y x khi x
x khi x

= +
+ +
Gọi là số kilomét di chuyển khi đó (nghìn đồng)
là số tiền phải trả được tính theo công thức:
Vận dụng 2.
c, Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến
trên khoảng nào.
Hàm số đồng biến trên  .
BÀI TẬP
6.1. Xét hai đại lượng phụ thuộc vào nhau theo các hệ thức dưới đây. Những
trường hợp nào thì là hàm số của ?
a) ; b)
; c)
; d)
.
Lời giải
Theo định nghĩa hàm số, mỗi giá trị có một và chỉ một giá trị tương ứng của
nên hệ thức ở câu a và câu b cho ta là hàm số của .
BÀI TẬP
6.2. Hãy cho một ví dụ về hàm số được cho bằng bảng hoặc biểu đồ.
Hãy chỉ ra tập xác định và tập giá trị của hàm số đó.
Lời giải
Ví dụ 1: Hàm số cho bởi bảng
Thống kê số ca mắc covid trong 10 ngày đầu tháng 8 năm 2021
(theo bản tin dịch covid-19 của Bộ y tế).
Ngày
1
2
3
4
5
6
7
8
9
10
Số ca
2025
2267
2173
935
1537
1497
2049
2002
1642
1466
Tập xác định 
Tập giá trị 󰇝󰇞.
Ví dụ 2: Hàm số cho bởi biểu đồ.
BÀI TẬP
6.3. Tìm tập xác định của các hàm số sau:
a, 

b,


c,
Lời giải
a, Tập xác định .
b, xác định
󰇫
Tập xác định 󰇝󰇞.
c, xác định 󰇫
󰇫

Tập xác định  .
BÀI TẬP
6.4. Tìm tập xác định và tập giá trị của mỗi hàm số sau:
a) ; b) 
.
Lời giải
b, Tập xác định .
Tập giá trị  .
a, Tập xác định .
Tập giá trị .
BÀI TẬP
6.5. Vẽ đồ thị của các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến
của chúng:
a) ; b)
.
Lời giải
a, Vẽ đồ thị hàm số  
Hàm số  nghịch biến trên .
BÀI TẬP
6.5. Vẽ đồ thị của các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến
của chúng:
a) ; b)
.
Lời giải
b, Vẽ đồ thị hàm số
.
Hàm số
đồng biến trên 󰇛󰇜 và
nghịch biến trên  .
BÀI TẬP
6.6. Giá thuê xe ô tô tự lái là 1,2 triệu đồng một ngày cho hai ngày đầu tiên
và 900 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền phải trả là một
hàm số của số ngày mà khách thuê xe.
a, Viết công thức của hàm số .
b, Tính và cho biết ý nghĩa của mỗi giá trị này.
Lời giải
a, Hàm số được cho bởi công thức
󰇫
󰇝󰇞
  
ở đó là số ngày thuê xe, 󰇛󰇜 là số tiền tính theo đơn vị nghìn đồng.
b, Theo công thức, ta có   .

Mô tả nội dung:


CHƯƠNG VI. CHƯƠNG I
HÀM SỐ - ĐỒ THỊ VÀ ỨNG DỤNG §15. Hàm số
§16. Hàm số bậc hai
§17. Dấu của tam thức bậc hai
§18. Phương trình quy về phương
trình bậc nhất bậc hai CHƯƠNG VI. CHƯƠNG I
HÀM SỐ - ĐỒ THỊ VÀ ỨNG DỤNG TOÁN ĐẠI SỐ 1 ➉ 15 HÀM SỐ 1 KHÁI NIỆM HÀM SỐ 1 2
ĐỒ THỊ CỦA HÀM SỐ 2 3
SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ 3 4 BÀI TẬP 4
1. KHÁI NIỆM HÀM SỐ
HĐ1:Bảng 6.1 cho biết nồng độ bụi PM 2.5 trong không khí theo thời gian trong
ngày 25-3-2021 tại một trạm quan trắc ở Thủ đô Hà Nội: Thời điểm (giờ) 0 4 8 12 16 Nồng độ bụi PM 2.5 ??/?3 74,27 64,58 57,9 69,07 81,78 Hướng dẫn:
Bảng 6.1 (Theo moitruongthudo. vn)
• Tại thời điểm 8 giờ nồng độ bụi là 57,9.
•Hãy cho biết nồng độ bụi PM 2.5 tại mỗi thời • điểm
Tại thời điểm 12 giờ nồng độ bụi là 69,07. 8 giờ, 12 giờ, 16 giờ.
•Trong Bảng 6.1, mỗi thời điểm tương ứng với
• Tại thời điểm 16 giờ nồng độ bụi là 81,78.
bao nhiêu giá trị của nồng độ bụi PM 2.5 ?
• Mỗi thời điểm tương ứng với một giá trị nồng độ bụi PM 2.5
1. KHÁI NIỆM HÀM SỐ
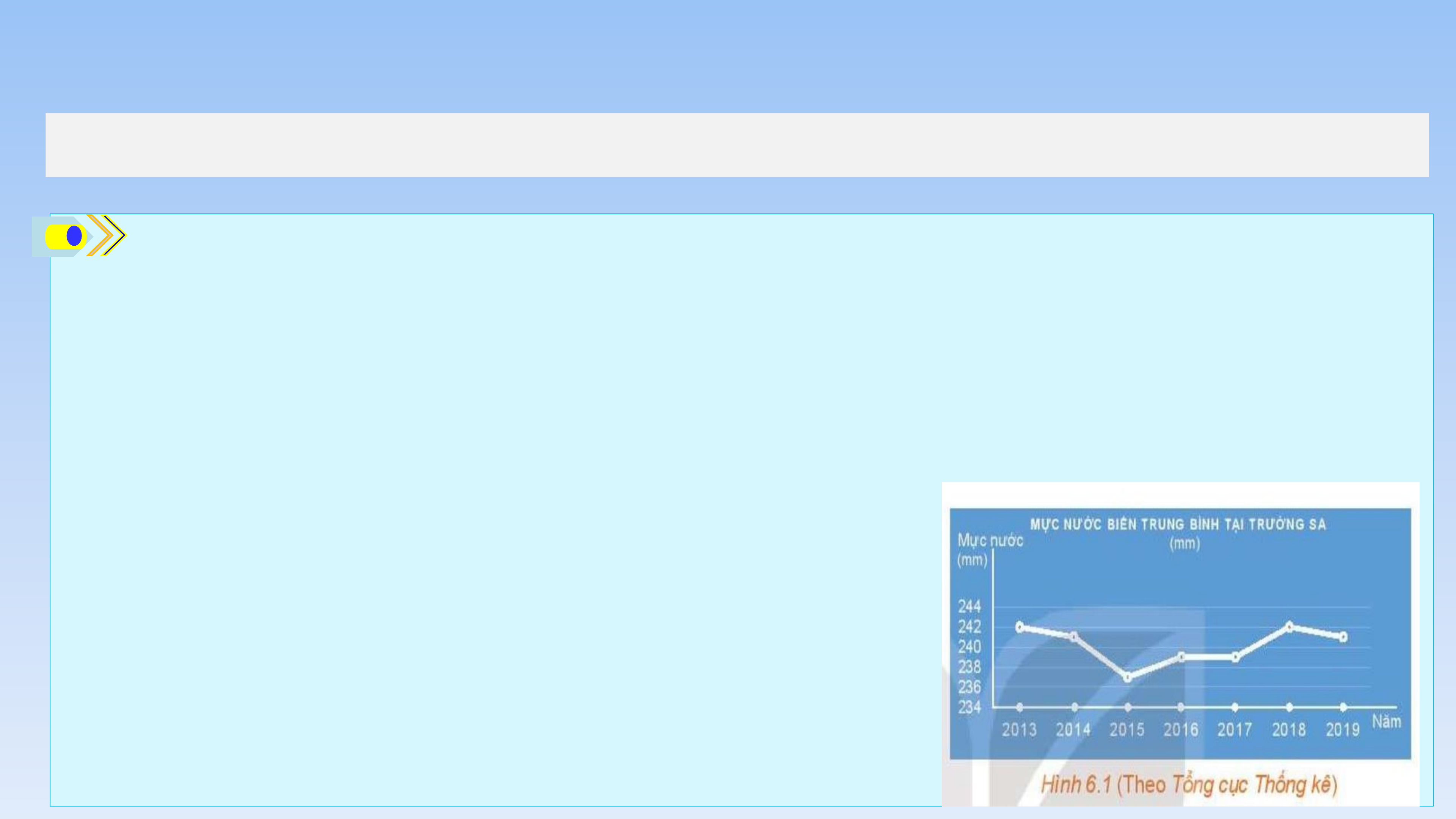
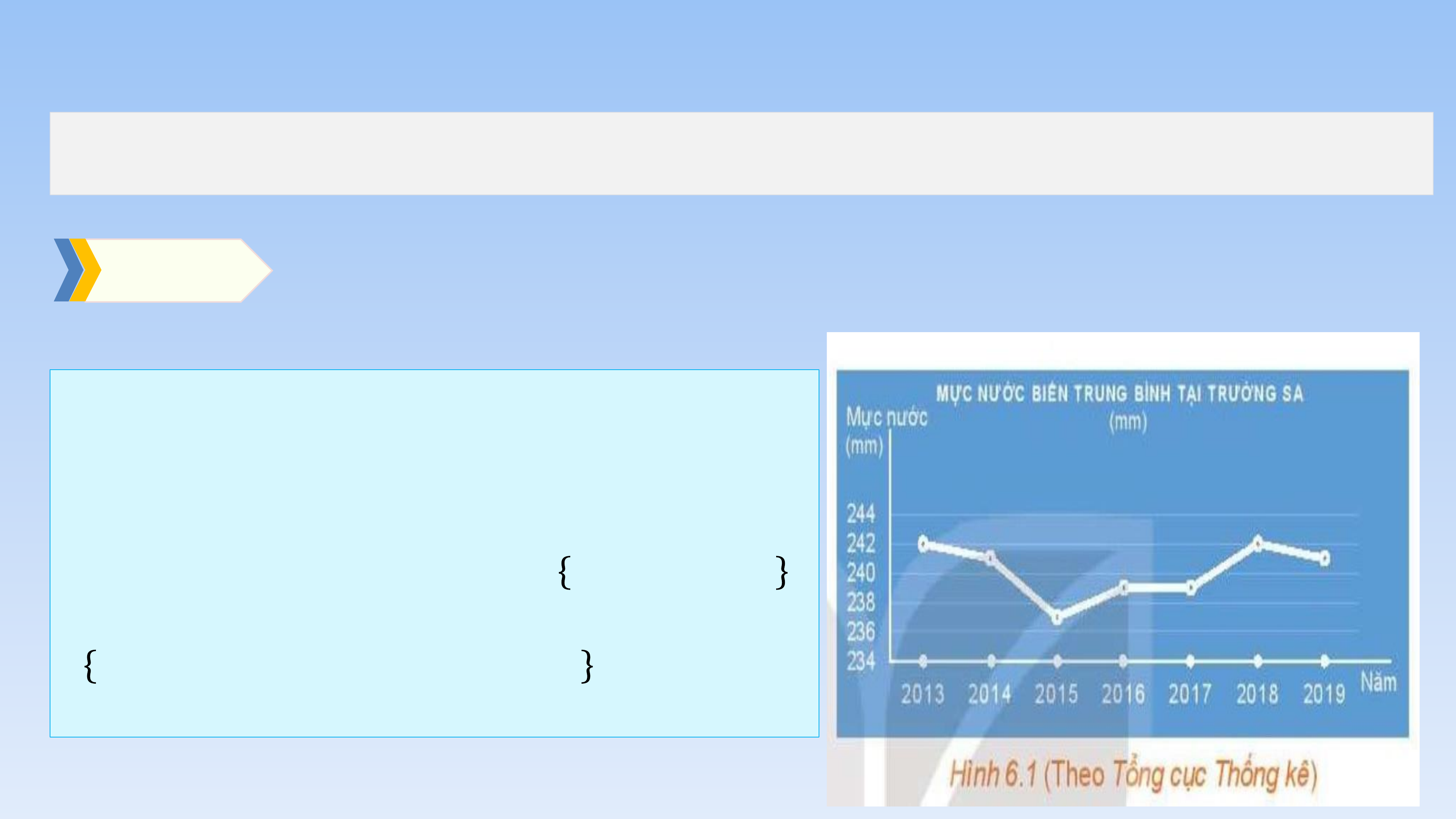
HĐ2: Quan sát Hình 6.1.
a) Thời gian theo dõi mực nước biển ở Trường Sa được thể hiện trong hình từ năm nào đến năm nào?
b) Trong khoảng thời gian đó, năm nào mực nước biển trung bình tại Trường Sa cao nhất, thấp nhất? Giải
Thời gian theo dõi mực nước biển ở Trường Sa được thể
hiện trong hình từ năm 2013 đến năm 2019.
Trong khoảng thời gian đó, năm 2013 và 2018 mực nước
biển trung bình tại Trường Sa cao nhất, năm 2015 thấp nhất.
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27
  • Slide 28
  • Slide 29
  • Slide 30
  • Slide 31
  • Slide 32
  • Slide 33
  • Slide 34
  • Slide 35
  • Slide 36
  • Slide 37
  • Slide 38
  • Slide 39
  • Slide 40
  • Slide 41

zalo Nhắn tin Zalo