CHƯƠNG VII. CHƯƠNG I
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG TOÁN HÌNH HỌC ➉ 20
VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG GÓC VÀ KHOẢNG CÁCH 1 1 1 I
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG II
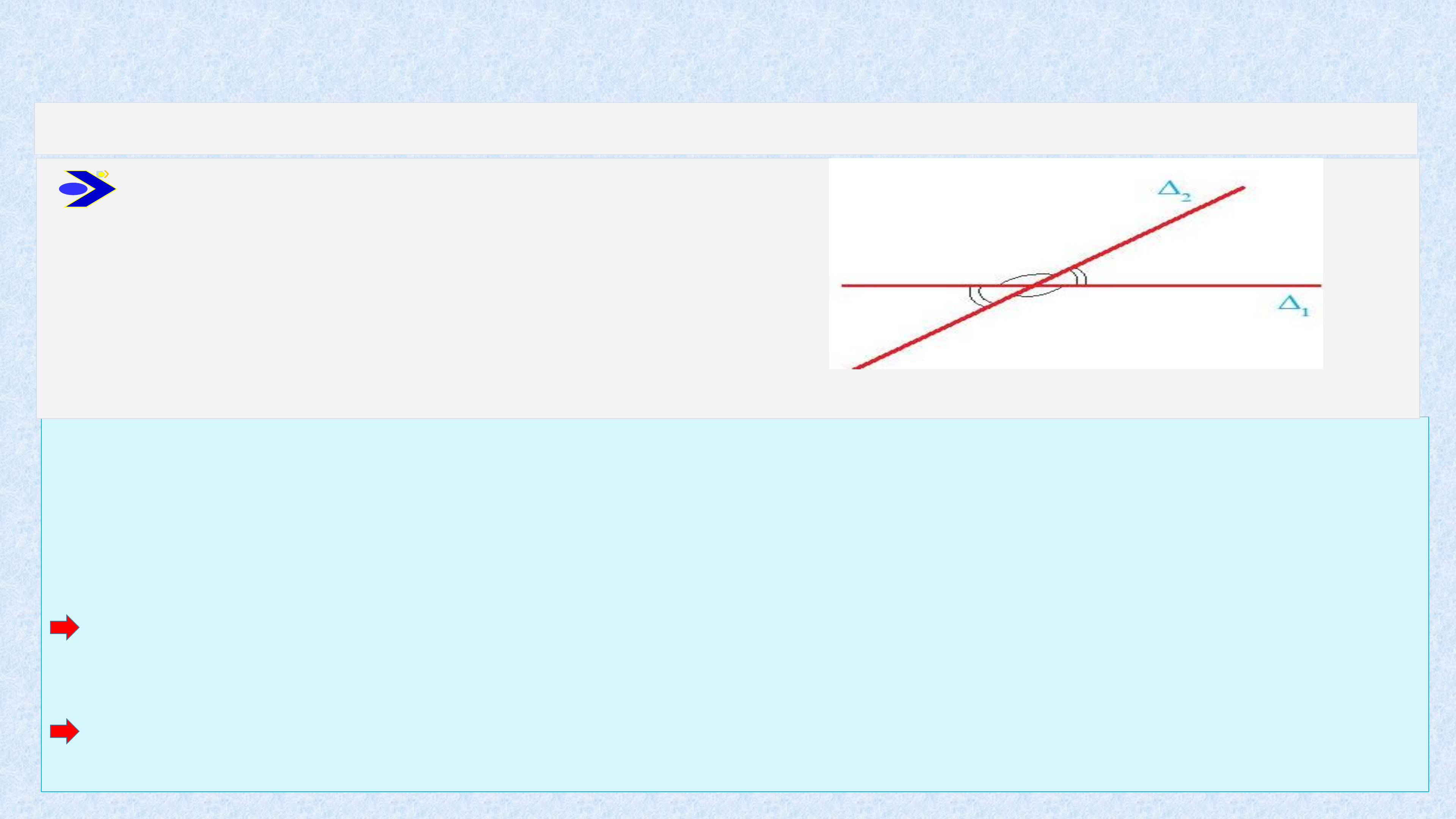
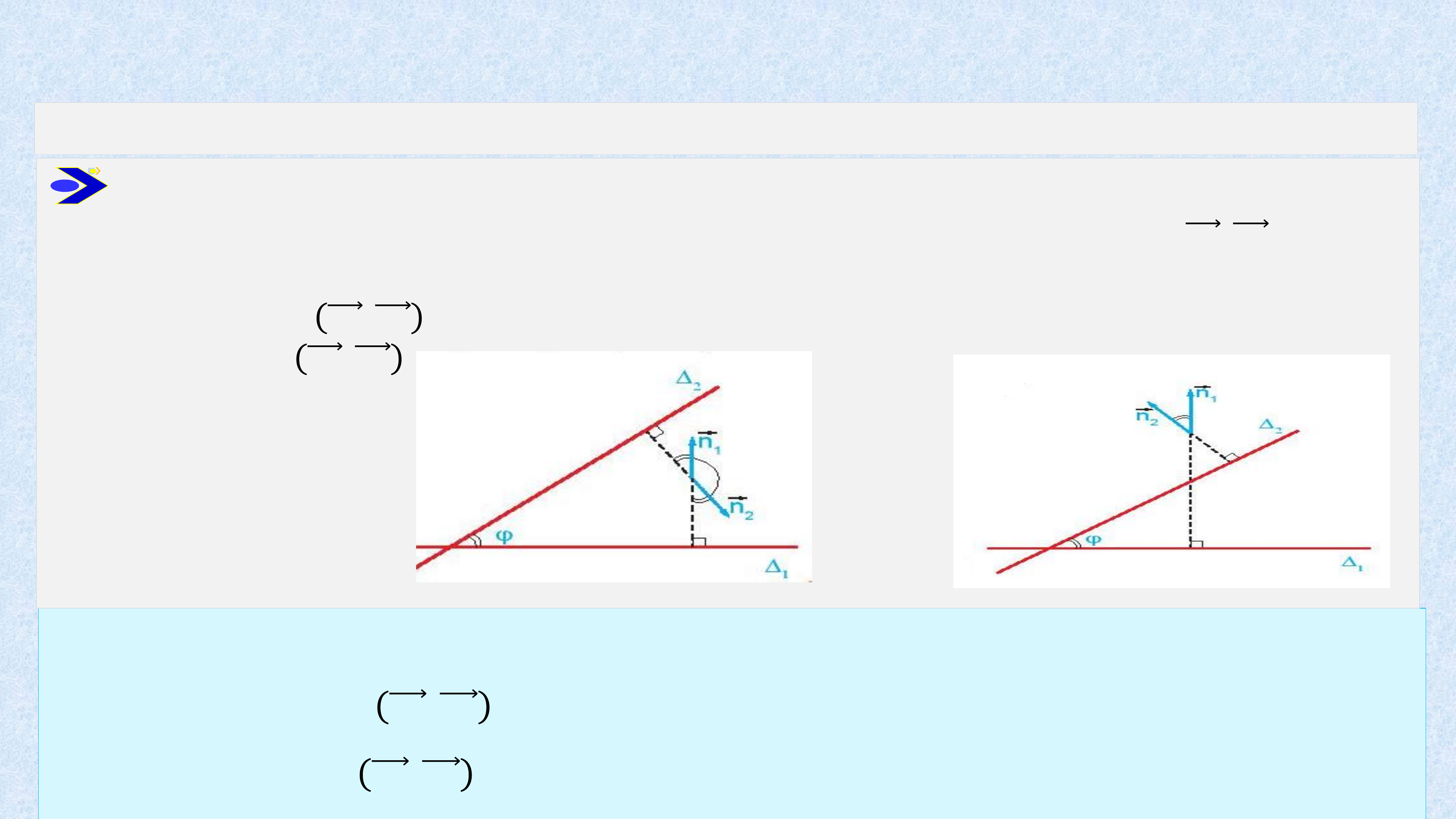
GÓC GIỮA HAI ĐƯỜNG THẲNG
III KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG 4 CHƯƠNG VII. CHƯƠNG I
PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG TOÁN HÌNH HỌC ➉ 20
VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG GÓC VÀ KHOẢNG CÁCH 1 1 1 THUẬT NGỮ
KIẾN THỨC, KỸ NĂNG • Góc, khoảng cách
• Nhận biết hai đường thẳng cắt nhau, song song, trùng
• Vị trí tương đối giữa hai nhau, vuông góc. đường thẳng
• Thiết lập công thức tính góc giữa hai đường thẳng.
• Tính khoảng cách từ một điểm đến một đường thẳng.
• Vận dụng các công thức tính góc và khoảng cách để giải 4
một số bài toán có liên quan đến thực tiễn.
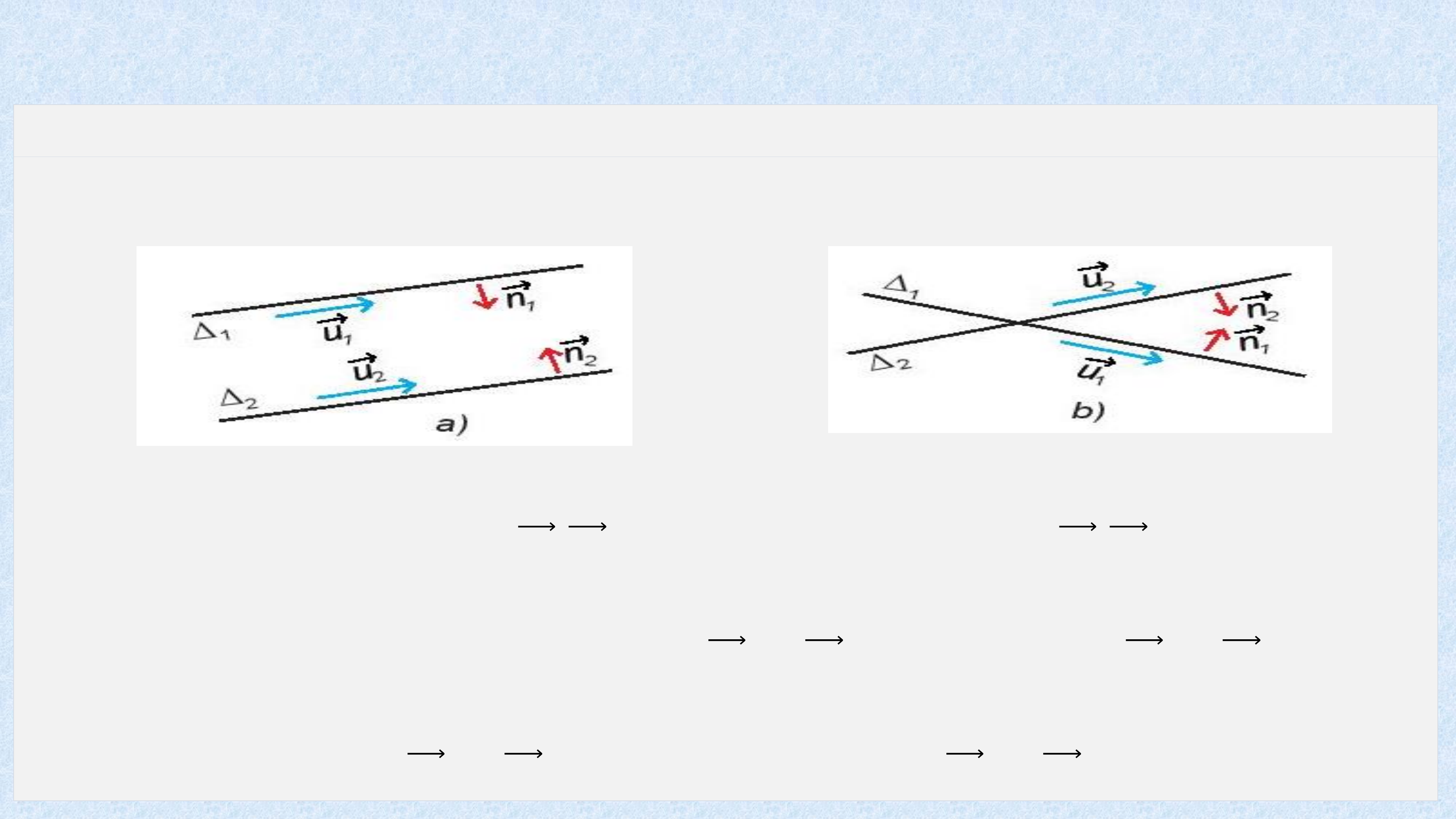
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
HĐ1: Trong mặt phẳng tọa độ, cho hai đường:
?1: ? − 2? + 3 = 0 và ?2: 3? − ? − 1 = 0.
a) Điểm ? 1; 2 có thuộc cả hai đường thẳng nói trên hay không?
b) Giải hệ ? − 2? + 3 = 0 ቊ3? − ? − 1 = 0
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của ? và với nghiệm của hệ phương 1 ?2 trình trên. Giải
a) Thay tọa độ điểm ? 1; 2 vào phương trình hai đường thẳng ? và , 1 ?2
ta được: 1 − 2.2 + 3 = 0 (đúng) ; 3.1 − 2 − 1 = 0(đúng).
Vậy điểm ? 1; 2 thuộc cả hai đường thẳng nói trên.
1. VỊ TRÍ TƯƠNG ĐỐI GIỮA HAI ĐƯỜNG THẲNG
HĐ1: Trong mặt phẳng tọa độ, cho hai đường:
?1: ? − 2? + 3 = 0 và ?2: 3? − ? − 1 = 0.
a) Điểm ? 1; 2 có thuộc cả hai đường thẳng nói trên hay không?
b) Giải hệ ? − 2? + 3 = 0 ቊ3? − ? − 1 = 0
c) Chỉ ra mối quan hệ giữa tọa độ giao điểm của ? và với nghiệm của hệ phương 1 ?2 trình trên. Giải b) ? − 2? + 3 = 0 ? − 2? = −3 ? = 1 ቊ ⇔ ቊ ⇔ ቊ . 3? − ? − 1 = 0 3? − ? = 1 ? = 2
c) Giao điểm của hai đường thẳng ? và chính là nghiệm của hệ phương trình trên. 1 ?2
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20