BÀI GIẢNG PPT
MÔN TOÁN – LỚP 10
BỘ SÁCH: CHÂN TRỜI SÁNG TẠO
Nhiệt liệt chào đón các em đến
với tiết học ngày hôm nay
Có thể phát biểu định
lí theo các cách nào khác? CHƯƠNG I:
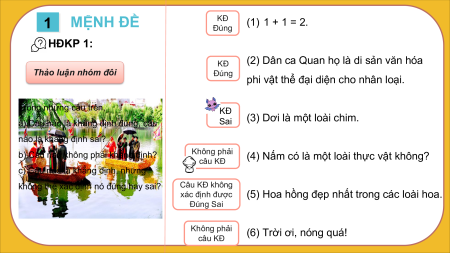
MỆNH ĐỀ VÀ TẬP HỢP
Bài giảng Powerpoint Toán 10 Học kì 1 Chân trời sáng tạo
813
407 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Bộ bài giảng điện tử Toán 10 Chân trời sáng tạo đã cập nhật đủ Cả năm.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Bộ tài liệu bao gồm: 26 tài liệu lẻ (mua theo bộ tiết kiệm đến 50%)
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Bộ bài giảng powerpoint Toán 10 Học kì 1 Chân trời sáng tạo bao gồm đầy đủ các bài giảng cả năm. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán 10 Chân trời sáng tạo.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(813 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Giáo án Toán 10 Kết nối tri thức (năng lực số)300.000 ₫ - 350.000 ₫ 22.7 K 11.3 K lượt tải
-
Chuyên đề dạy thêm Toán 10 Kết nối tri thức mới nhất300.000 ₫ 12 K 6 K lượt tải
-
Bộ 3 đề thi khảo sát chất lượng đầu năm Toán 10 năm 2025 (có đáp án)60.000 ₫ 2.2 K 1.1 K lượt tải
-
Bộ 20 đề thi cuối kì 2 Toán 10 Kết nối tri thức Cấu trúc mới150.000 ₫ - 200.000 ₫ 42.5 K 21.3 K lượt tải
-
Bài giảng Powerpoint Toán 10 Kết nối tri thức (phiên bản 2350.000 ₫ 372 186 lượt tải
-
Bài tập trắc nghiệm Toán 10 Kì 2 Kết nối tri thức (có đáp án130.000 ₫ 1.1 K 552 lượt tải
-
30 đề thi Toán 10 Giữa kì 2 có lời giải (sách mới180.000 ₫ 538 269 lượt tải
-
Lý thuyết Toán 10 Kết nối tri thức (cả năm)150.000 ₫ 1.3 K 662 lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 10
Xem thêm-
Chuyên đề dạy thêm Vật lí 10 (sách mới) có đáp án200.000 ₫ 10.5 K 5.2 K lượt tải
-
Bài giảng Powerpoint Tiếng Anh 10 Global success300.000 ₫ 13.5 K 6.8 K lượt tải
-
Giáo án KTPL 10 Kết nối tri thức (năng lực số)300.000 ₫ 7.7 K 3.8 K lượt tải
-
Bộ đề thi cuối kì 2 Vật lí 10 Chân trời sáng tạo có đáp án70.000 ₫ 7.2 K 3.6 K lượt tải
-
Giáo án Sinh học 10 Kết nối tri thức | Giáo án Sinh học 10 mới chuẩn nhất200.000 ₫ 6.8 K 3.4 K lượt tải
-
Bộ 18 đề thi giữa kì 1 Tiếng Anh 10 Global Success có đáp án150.000 ₫ 16.3 K 8.1 K lượt tải
-
Bài giảng Powerpoint KTPL 10 Kết nối tri thức350.000 ₫ 4.9 K 2.4 K lượt tải
-
Khung năng lực số môn Hóa học 10 (mới nhất)30.000 ₫ 388 194 lượt tải
Nhắn tin Zalo