Bài giảng Powerpoint Toán 10 Học kì 2 Chân trời sáng tạo

618 309 lượt tải
Chia sẻ Facebook Báo cáo tài liệu
Lớp: Lớp 10
Môn: Toán Học
Bộ sách: Chân trời sáng tạo
Dạng: Giáo án, Giáo án Powerpoint
File:
Loại: Bộ tài liệu bao gồm: 18 TL lẻ ( Xem chi tiết » )

CÁCH MUA:

  • B1: Gửi phí vào TK: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
  • B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án

Liên hệ ngay Hotline hỗ trợ: 084 283 45 85

Bộ bài giảng điện tử Toán 10 Chân trời sáng tạo đã cập nhật đủ Cả năm. 

Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!

  • Bộ bài giảng powerpoint Toán 10 Học kì 2 Chân trời sáng tạo bao gồm đầy đủ các bài giảng cả năm. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán 10 Chân trời sáng tạo.
  • Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.

Đánh giá

4.6 / 5(618 )
5
53%
4
22%
3
14%
2
5%
1
7%
Trọng Bình
Tài liệu hay

Giúp ích cho tôi rất nhiều

Duy Trần
Tài liệu chuẩn

Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)

TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học

Xem thêm

TÀI LIỆU BỘ BÁN CHẠY Lớp 10

Xem thêm

Tài liệu bộ mới nhất

TẢI NGAY
Lớp 9 Toán Học

Bộ 10 đề thi Cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án

(5.0)

Miễn phí
15
TẢI NGAY
Lớp 9 Toán Học

Bộ 10 đề thi Cuối kì 1 Toán 9 Cánh diều có đáp án

(5.0)

Miễn phí
9
TẢI NGAY
Lớp 9 Toán Học

Bộ 10 đề thi Cuối kì 1 Toán 9 Kết nối tri thức có đáp án

(5.0)

180.000 ₫
24 47
TẢI NGAY
Lớp 10 Toán Học

Đề cương ôn tập Cuối kì 1 Toán 10 Kết nối tri thức

(5.0)

80.000 ₫
17 34
TẢI NGAY
Lớp 10 Toán Học

Đề cương ôn tập Cuối kì 1 Toán 10 Cánh diều

(5.0)

80.000 ₫
14 27
TẢI NGAY
Lớp 10 Toán Học

Đề cương ôn tập Cuối kì 1 Toán 10 Chân trời sáng tạo

(5.0)

80.000 ₫
14 28
TẢI NGAY
Lớp 10 Toán Học

5 đề thi Toán 10 Cuối kì 1 Chân trời sáng tạo cấu trúc mới

(5.0)

90.000 ₫
51 101
TẢI NGAY
Lớp 10 Toán Học

5 đề thi Toán 10 Cuối kì 1 Cánh diều cấu trúc mới

(5.0)

90.000 ₫
42 84
TẢI NGAY
Lớp 10 Toán Học

5 đề thi Toán 10 Cuối kì 1 Kết nối tri thức cấu trúc mới

(5.0)

90.000 ₫
31 61
TẢI NGAY
Lớp 9 Toán Học

Bộ 5 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo (form Hà Nội)

(5.0)

150.000 ₫
38 76
CHÀO MỪNG CÁC EM
ĐẾN VỚI BUỔI HỌC
NGÀY HÔM NAY!
KHỞI ĐỘNG
Cầu vòm được thiết kế với thanh vòm hình parabol và mặt cầu đi ở
giữa. Trong hệ trục tọa độ Oxy như hình vẽ, phương trình của vòm
cầu là y = h(x) = -0,006x
2
+ 1,2x – 30. Với giá trị h(x) như thế nào tại
vị trí x (0 x 200), vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu,
CHƯƠNG VII.
BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
BÀI 1: DẤU CỦA TAM THỨC BẬC HAI
NỘI DUNG BÀI HỌC
Tam thức bậc hai
Định lí dấu của tam thức bậc hai
Tam thức bậc hai
HĐKP 1:
Đồ thị của hàm số   
 được biểu diễn trong Hình 1.
a) Biểu thức là đa thức bậc mấy?
b) Xác định dấu của
Trả lời
a) Biểu thức   
  được
biểu diễn trong Hình 1 là đa thức bậc hai.
b) Có:
   
Vậy f(2) mang dấu dương.
KẾT LUẬN
Đa thức bậc hai f(x) = ax
2
+ bx + c với a, b, c
là các hệ số, a 0 và x là biến số được gọi
là tam thức bậc hai.
CHÚ Ý
Cho tam thức bậc hai f(x) = ax
2
+ bx + c (a 0). Khi thay x bằng
giá trị x
0
vào f(x), ta được f(x
0
) = a x
0
2
+ bx
0
+ c, gọi là giá trị của
tam thức bậc hai tại x
0
.
- Nếu f(x
0
) > 0 thì ta nói f(x) dương tại x
0
.
- Nếu f(x
0
) < 0 thì ta nói f(x) âm tại x
0
.
- Nếu f(x) dương (âm) tại mọi điểm x thuộc một khoảng hoặc
một đoạn thì ta nói f(x) dương (âm)trên khoảng hoặc đoạn đó.
Ví dụ 1 (SGK – tr7)
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy
xét dấu của nó tại .
a) 󰇛󰇜 

b) 󰇛󰇜 

Giải
a) Biểu thức 󰇛󰇜 
là một tam thức bậc hai.
nên 󰇛󰇜 dương tại .
󰇛󰇜 
b) Biểu thức 󰇛󰇜 

không phải là một tam thức bậc hai.
THỰC HÀNH 1
Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy
xét dấu của nó tại x = 1.
󰇜 
 
󰇜 


󰇜󰇛󰇜

THẢO LUẬN
NHÓM
f(1) =2.1
2
+ 1−1 = 2 > 0
h(1) = −1
2
+ 1 – 3
= −4 + -2,6 < 0
h(x) âm tại x = 1.
f(x) dương tại x = 1
KẾT LUẬN
Cho tam thức bậc hai f(x) = ax
2
+ bx + c (a 0). Khi đó:
• Nghiệm của phương trình bậc hai ax
2
+ bx + c = 0 là
nghiệm của f(x).
• Biểu thức = b
2
– 4ac và
󰆒
- ac lần lượt là biệt thức
và biệt thức thu gọn của f(x)
Ví dụ 2 (SGK – tr7)
Giải
Tìm biệt thức và nghiệm của các tam thức bậc hai sau:
a) 󰇛󰇜

b) 󰇛󰇜 
c) 󰇛󰇜 
a) Tam thức bậc hai 󰇛󰇜
 có
 󰇛󰇜 
 
 à
 

Do đó, 󰇛󰇜 có hai nghiệm phân biệt là
Giải
b) Tam thức bậc hai 󰇛󰇜 
có
 .
c) Tam thức bậc hai 󰇛󰇜 
Có
 󰇛󰇜

Vì nên 󰇛󰇜 vô nghiệm.
Do đó, h(x) có nghiệm kép là
.
THỰC HÀNH 2
THẢO LUẬN
NHÓM
Tìm biệt thức và nghiệm của tam thức bậc hai sau:
Giải
a) Tam thức bậc hai 󰇛󰇜 
 có :
󰇛󰇜
 >0
f(x) có hai nghiệm phân biệt là:
󰇛󰇜

và
󰇛󰇜

󰇜 
  
󰇜 
 
󰇜 
  
Giải
b) Tam thức bậc hai 󰇛󰇜 
 có :
󰇛󰇜
 󰇛󰇜 󰇛󰇜
g(x) có nghiệm kép là:

 󰇛󰇜
c) Tam thức bậc hai 󰇛󰇜 
 có :
󰇛󰇜
  < 0
g(x) vô nghiệm.
Định lí dấu của tam thức bậc hai
Quan sát đồ thị của các hàm số bậc
hai trong các hình dưới đây. Trong mỗi
trường hợp hãy cho biết:
- Các nghiệm (nếu có) và dấu của
biệt thức ∆.
- Các khoảng giá trị của x mà trên đó
f(x) cùng dấu với hệ số của
HĐKP 2:
THẢO LUẬN NHÓM
Giải
• Hình a:
󰇛󰇜 

f(x) vô nghiệm
Có a = -1 < 0; f(x) < 0, mọi
• Hình b:
󰇛󰇜 

f(x) có nghiệm kép x
1
= x
2
= 1
Có a = -1 <0; f(x) <0, mọi \{1}
• Hình c:
• Hình d:
f(x) có hai nghiệm phân biệt:
x
1
= -1 và x
2
= 3.
Có: a = -1 < 0; f(x) < 0
khi  
󰇛󰇜 

; f(x) vô nghiệm.
󰇛󰇜
 
Có: a = 1 > 0; f(x) > 0 mọi
• Hình e:
• Hình g:
f(x) có nghiệm kép x
1
= x
2
= -3
󰇛󰇜

f(x) có hai nghiệm phân biệt:
x
1
= -4 và x
2
= -2.
Có: a = 1 > 0; f(x) > 0 khi
 
󰇛󰇜

Có: a = 1 > 0; f(x) > 0 mọi \{-3}
KẾT LUẬN
Cho tam thức bậc hai f(x) = ax
2
+ bx + c (a 0)
• Nếu  thì f(x) cùng dấu với a với mọi giá trị x.
• Nếu  và x
0
=


là nghiệm kép của f(x) thì f(x) cùng
dấu với a với mọi x khác x
0
.
• Nếu  và x
1
; x
2
là hai nghiệm của f(x) (x
1
< x
2
) thì f(x)
trái dấu với a với mọi x trong khoảng (x
1
; x
2
); f(x) cùng
dấu với a với mọi x thuộc hai khoảng (-; x
1
) ; (x
2
; +).
CHÚ Ý
Để xét dấu tam thức bậc hai f(x) = ax
2
+bx+c (a 0), ta thực hiện
các bước sau:
Bước 1: Tính và xác định dấu của biệt thức ;
Bước 2: Xác định nghiệm của f(x) (nếu có);
Bước 3: Xác định dấu của hệ số a;
Bước 4: Xác định dấu của f(x).
Ví dụ 3 (SGK – tr9)
Giải
Xét dấu của các tam thức bậc hai sau:
a) 󰇛󰇜 
  có  , hai nghiệm phân biệt là

và  .
Vậy 󰇛󰇜 dương trong khoảng 󰇛 󰇜 và âm trong hai khoảng 󰇛 󰇜 và 󰇛 󰇜
a) 
  b)
  c) 󰇛󰇜 

Ta có bảng xét dấu 󰇛󰇜 như sau:
Ví dụ 3 (SGK – tr9)
Giải
Xét dấu của các tam thức bậc hai sau:
a) 
  b)
  c) 󰇛󰇜 

b) 󰇛󰇜 
 có , nghiệm kép là
và .
c) 󰇛󰇜 
 có  và .
Vậy 󰇛󰇜 dương với mọi .
Vậy 󰇛󰇜 dương với mọi
.
THỰC HÀNH 3
Giải
Xét dấu của tam thức bậc hai sau:
󰇜 
   󰇜

a) 󰇛󰇜 
 có:  > 0, hai nghiệm phân biệt là x
1
=

và

Ta có bảng xét dấu f(x) như sau:
x

f(x)
Vậy f(x) dương trong khoảng (;

) (

; ) và âm trong khoảng (

; 2).
THỰC HÀNH 3
Giải
Xét dấu của tam thức bậc hai sau:
󰇜 
   󰇜

b) 󰇛󰇜 
 có:  < 0 và a = -1 < 0.
Vậy g(x) âm với mọi .
BÀI TẬP VẬN DỤNG
Xét dấu tam thức bậc hai 
  trong bài toán
khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu:
cao hơn mặt cầu, thấp hơn mặt cầu.
THẢO LUẬN
NHÓM
Giải
󰇛󰇜 
 
có:


hai nghiệm phân biệt là:



  



 
Ta có bảng xét dấu f(x) như sau:
x
    
f(x)
Vậy vòm cầu cao hơn mặt cầu khi và thấp hơn
mặt cầu khi       .
    
LUYỆN TẬP
Bài 1 (SGK – trang 9)
Đa thức nào sau đây là tam thức bậc hai?
󰇜
 
󰇜


󰇜 

LUYỆN TẬP
Bài 2 (SGK – trang 9)
Xác định giá trị của m để đa thức
sau là tam thức bậc hai.
Giải
󰇜 
 
󰇜

󰇜

c) 
 là tam thức bậc
hai với mọi m.
a) 󰇛 󰇜
 là tam thức
bậc hai khi

b)

là tam thức
bậc hai khi
m
LUYỆN TẬP
Bài 3 (SGK – trang 10) Dựa vào đồ thị của các hàm số bậc hai sau đây,
hãy lập bảng xét dấu của tam thức bậc hai tương ứng.
Giải
a)
󰇛󰇜
 có

Hai nghiệm phân biệt là
 ;
và a = 1 > 0
Ta có bảng xét dấu f(x) như sau:
x


f(x)
Vậy f(x) dương trong hai khoảng 
và 
và âm trong khoảng
.
Giải
b)
Ta có bảng xét dấu g(x) như sau:
󰇛󰇜
có  và a =1 > 0
x

g(x)
Vậy f(x) dương với mọi
Giải
c)
Ta có bảng xét dấu h(x) như sau:
󰇛󰇜 
 có
Nghiệm kép là

và 
x


h(x)
Vậy f(x) âm với mọi

Giải
d)
Ta có bảng xét dấu f(x) như sau:
󰇛󰇜 
 có 
và 
x

f(x)
Vậy f(x) âm với mọi
Giải
e)
Ta có bảng xét dấu g(x) như sau:
󰇛󰇜 
 có

Hai nghiệm phân biệt là
 ;
và a = -1 < 0
x


f(x)
Vậy f(x) dương trong hai khoảng  và

và âm trong khoảng 
.
Giải
g)
Ta có bảng xét dấu h(x) như sau:
Nghiệm kép là
và a = -9 < 0
󰇛󰇜
 có

Vậy f(x) âm với mọi
LUYỆN TẬP
Bài 4 (SGK – trang 10)
󰇜    
Xét dấu của tam thức bậc hai sau đây:
󰇜 
 
󰇜 
 
󰇜 
 
󰇜    
󰇜 
 
Giải
Có =
- 4.2.2 = 0.
Phương trình có nghiệm kép:
Mặt khác a = 2 > 0
Nên f(x) luôn dương với mọi x khác -1



Có: a = -3 < 0
󰇜 
 
Có =
- 4(-3).21 = 256 > 0
Phương trình có hai nghiệm phân biệt:
 
 


f(x) mang dấu dương khi x nằm trong
khoảng và mang dấu âm trong



hai khoảng và
Giải
Mặt khác a = - 2 < 0
Nên f(x) luôn âm với mọi x
Có: 
Phương trình có hai nghiệm kép:
󰇜 
 
Có = 󰇛󰇜
󰇛󰇜󰇛󰇜 
f(x) mang dấu âm với mọi x khác -1,5
󰇜    
Có = 󰇛󰇜
󰇛󰇜󰇛󰇜 

Giải
󰇜   
Có a = 2 > 0

 
Có 󰇛󰇜
 󰇛󰇜 
Nên phương trình có 2 nghiệm phân biệt:
 


 


 f(x) dương trong hai khoảng và


và âm trong khoảng

BÀI TẬP TRẮC NGHIỆM
Câu 1. Biểu thức nào sau đây là tam thức bậc hai?
A. .  B.

C .

 . D.
 .
BÀI TẬP TRẮC NGHIỆM
Câu 2: Bảng xét dấu nào sau đây là bảng xét dấu của tam thức

?
A.
x
 3 
f(x)
B.
x
 3 
f(x)
C.
x   2 
f(x)
D.
x
 2 
f(x)
BÀI TẬP TRẮC NGHIỆM
Câu 3: Cho tam thức bậc hai 
 . Tìm tất cả
giá trị của để
A.  󰇜
󰇜
󰇛 . B.  .
C.  . D.  .
BÀI TẬP TRẮC NGHIỆM
Câu 4: Cho 󰇛󰇜
 . Mệnh đề nào sau đây là đúng?
A. 󰇛󰇜   B. 󰇛󰇜  
C. 󰇛󰇜   D. 󰇛󰇜  
BÀI TẬP TRẮC NGHIỆM
A. với và với hoặc .
B. với   và với hoặc .
C. với và với hoặc .
D. với   và với hoặc .
Câu 5: Dấu của tam thức bậc 2: 
 được xác định
như sau
VẬN DỤNG
Bài 5 (SGK – trang 10)
Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi bóng di
chuyển được x mét theo phương ngang được mô phỏng bằng hàm
số 
 . Trong các khoảng nào của x thì bóng nằm:
cao hơn vành rổ, thấp hơn vành rổ và ngang vành rổ? Làm tròn kết quả
đến hàng phần mười.
Giải
Hàm số h(x) có =
– 4.(-0,1)(-1) = 0,6 > 0
nên sẽ có hai nghiệm phân biệt :
= 9,
= 1
và 
- Bóng nằm cao hơn vành rổ khi bóng nằm trong khoảng (1;9)
- Bóng nằm thấp hơn vành rổ khi bóng nằm trong khoảng (-; 1) và (9; +)
- Bóng nằm ngang vành rổ khi bóng ở độ cao 1m hoặc 9m
Vậy :
VẬN DỤNG
Bài 6 (SGK – trang 10)
Một khung dây thép hình chữ nhật có chiều dài 20 cm và chiều rộng
15 cm được uốn lại thành khung hình chữ nhật mới có kích thước
(20 + x) cm và (15 – x) cm. Với x nằm trong các khoảng nào thì
diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi?
Giải
Diện tích của khung dây thép khi chưa uốn là : 20.15 = 300 (
)
Diện tích của khung dây thép khi đã uốn là : 󰇛 󰇜 󰇛 󰇜  
.
Như vậy diện tích của khung sau khi uốn tùy thuộc vào giá trị của hàm số
f(x) = 
Xét hàm số f(x) có =
 
có hai nghiệm phân biệt:
và có a = 1 > 0. Nên :
 


 

Giải
• f(x) mang dấu dương khi x thuộc (-5;0)
Diện tích khung hình sau khi uốn nhỏ hơn trước khi uốn (giảm đi)
• f(x) mang dấu âm khi x thuộc (-20; -5) và (0 ; 15)
Diện tích khung hình sau khi uốn lớn hơn trước khi uốn (tăng lên)
• f(x) = 0 khi x = 0 hoặc x = -5
Diện tích khung hình sau khi uốn và trước khi uốn là không thay đổi
HƯỚNG DẪN VỀ NHÀ
* Ghi nhớ
kiến thức trong bài.
* Hoàn thành các
bài tập trong SBT.
* Chuẩn bị trước
“Bài 2: Giải bất
phương trình bậc hai
một ẩn”
CẢM ƠN CÁC EM
ĐÃ LẮNG NGHE BÀI HỌC!

Mô tả nội dung:


CHÀO MỪNG CÁC EM
ĐẾN VỚI BUỔI HỌC NGÀY HÔM NAY! KHỞI ĐỘNG
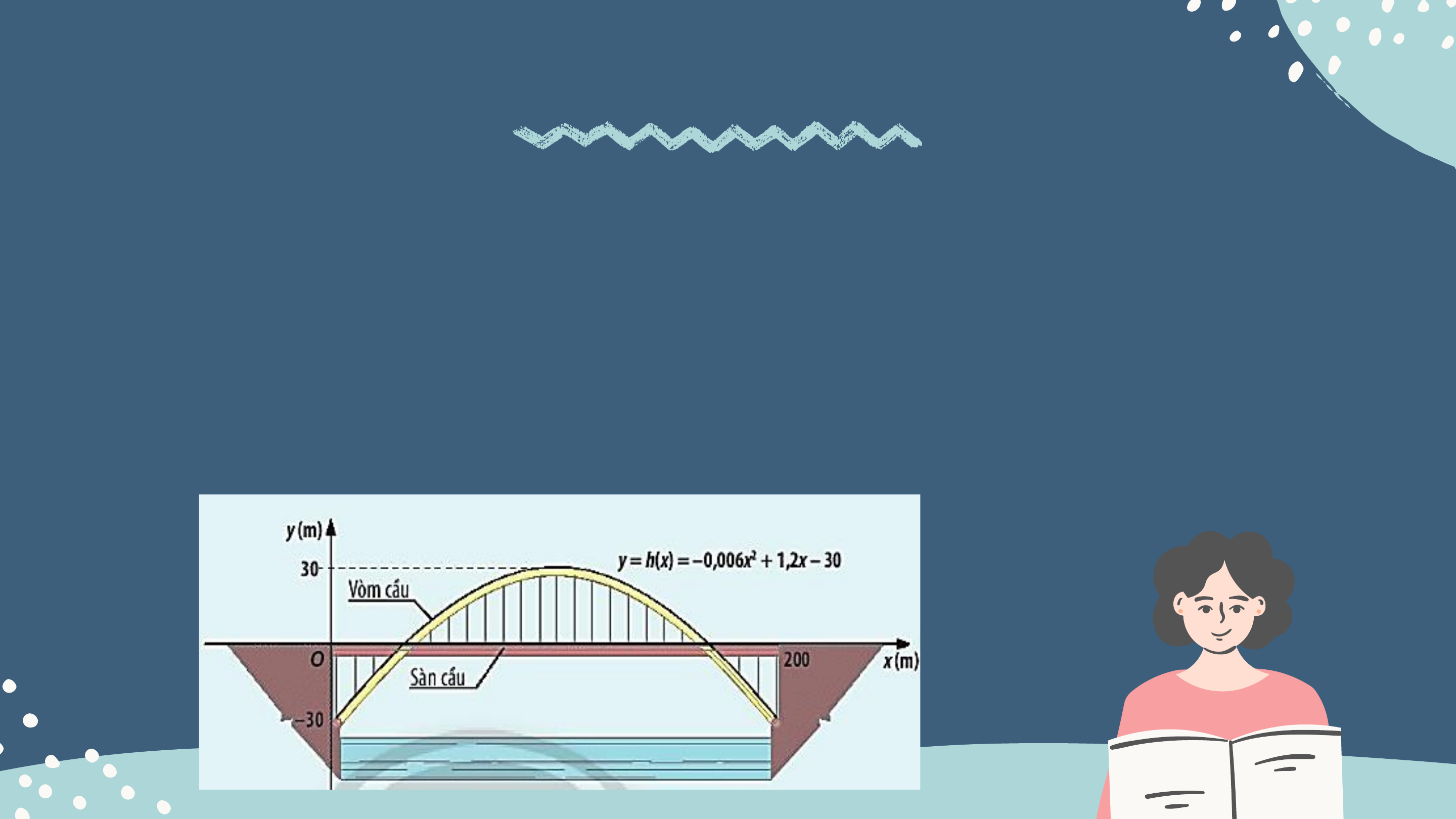
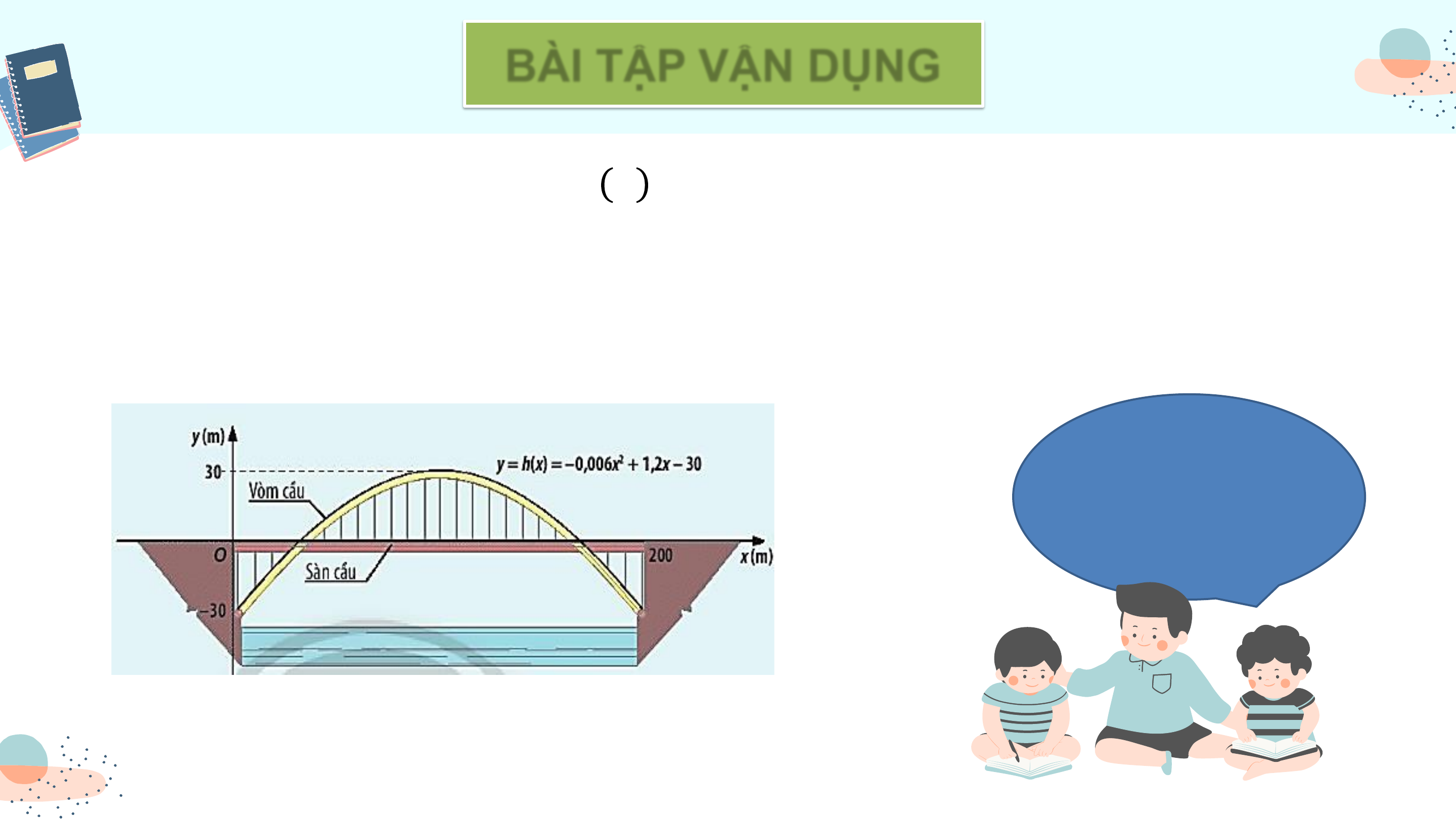
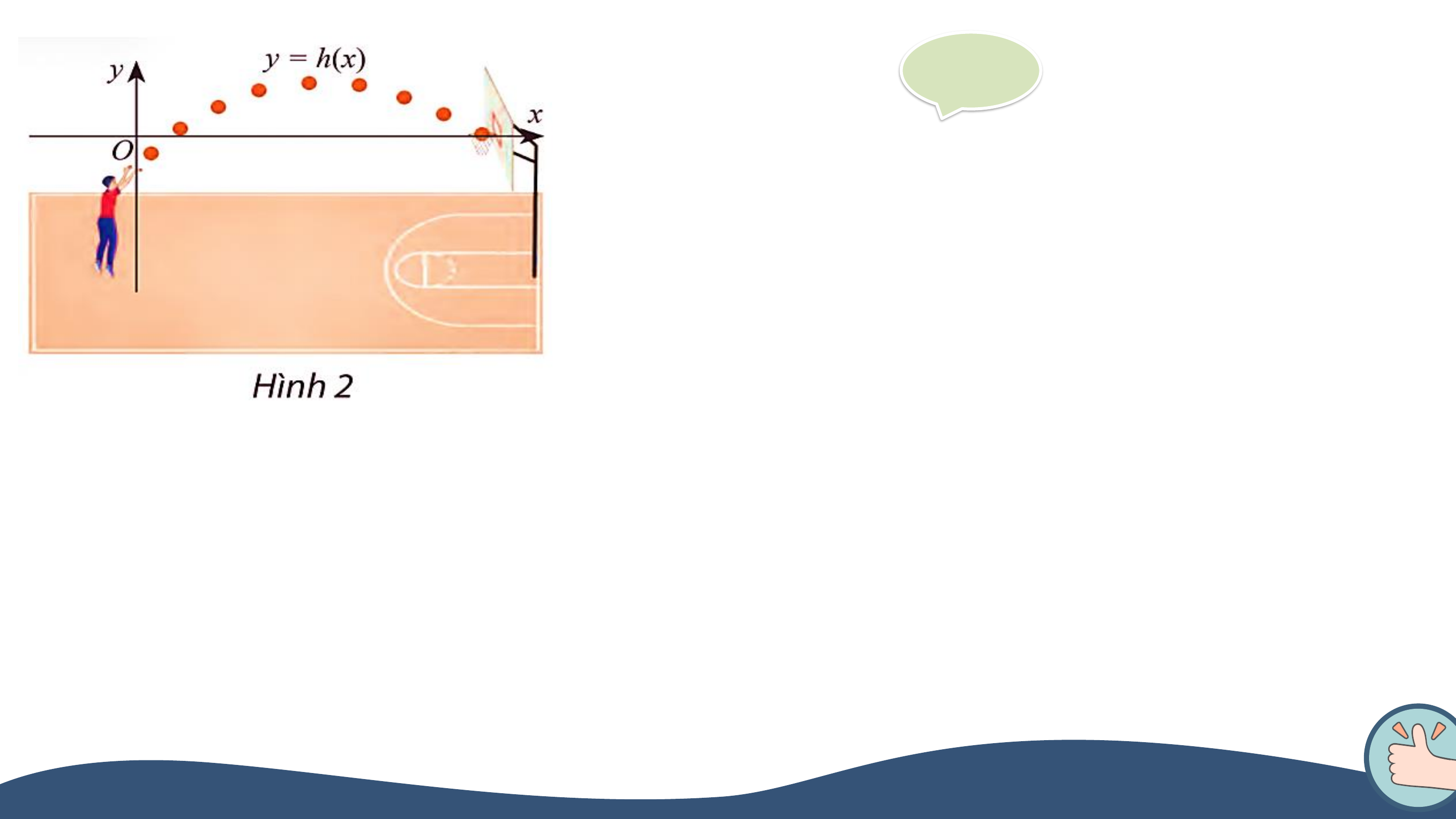
Cầu vòm được thiết kế với thanh vòm hình parabol và mặt cầu đi ở
giữa. Trong hệ trục tọa độ Oxy như hình vẽ, phương trình của vòm
cầu là y = h(x) = -0,006x2 + 1,2x – 30. Với giá trị h(x) như thế nào tại
vị trí x (0 ≤ x ≤ 200), vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu, CHƯƠNG VII.
BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
BÀI 1: DẤU CỦA TAM THỨC BẬC HAI NỘI DUNG BÀI HỌC Tam thức bậc hai
Định lí dấu của tam thức bậc hai
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27
  • Slide 28
  • Slide 29
  • Slide 30
  • Slide 31
  • Slide 32
  • Slide 33
  • Slide 34
  • Slide 35
  • Slide 36
  • Slide 37
  • Slide 38
  • Slide 39
  • Slide 40
  • Slide 41
  • Slide 42
  • Slide 43
  • Slide 44
  • Slide 45
  • Slide 46
  • Slide 47
  • Slide 48
  • Slide 49
  • Slide 50
  • Slide 51

zalo Nhắn tin Zalo