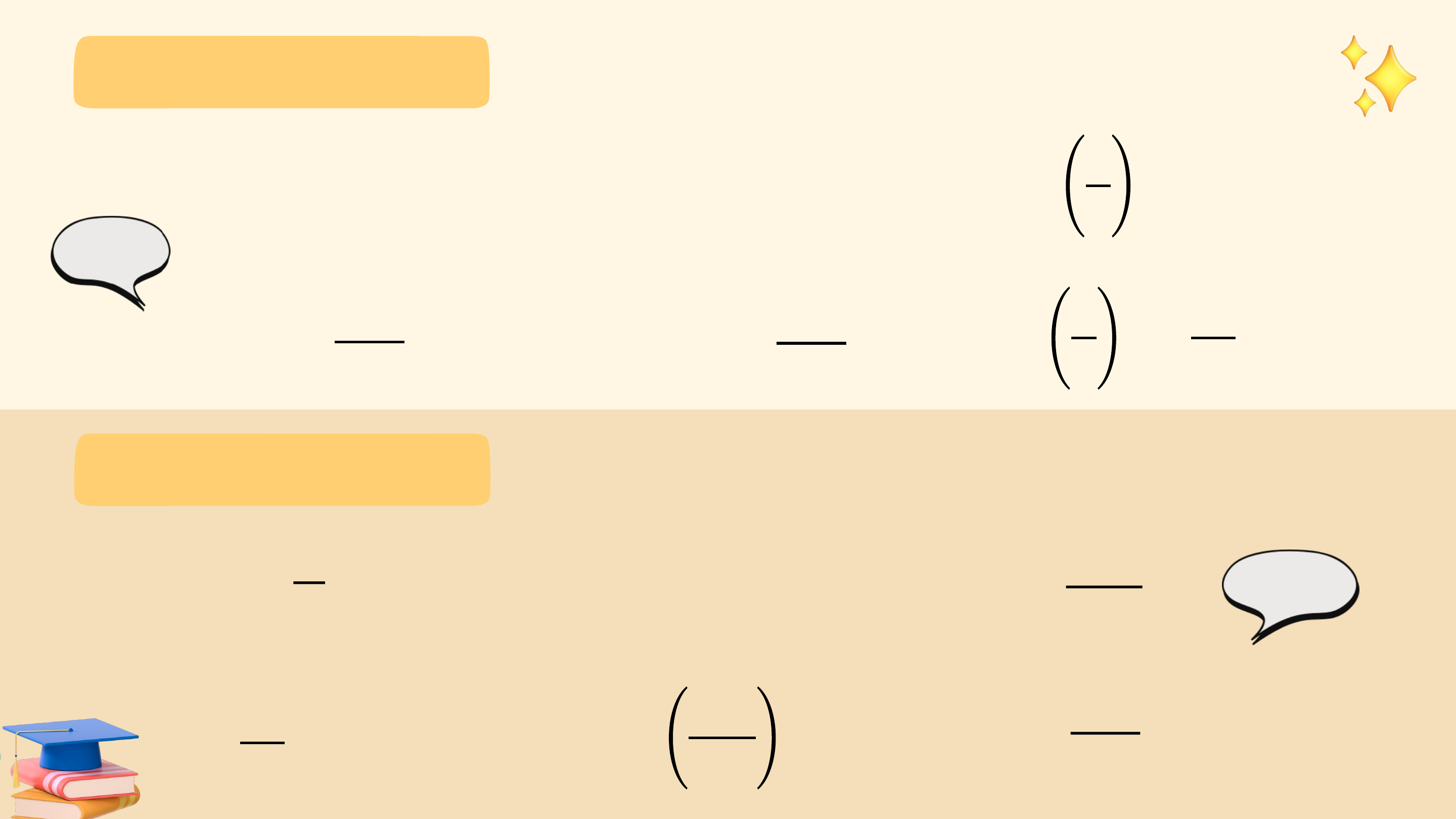CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI HỌC HÔM NAY! KHỞI ĐỘNG • Tình huống mở đầu:
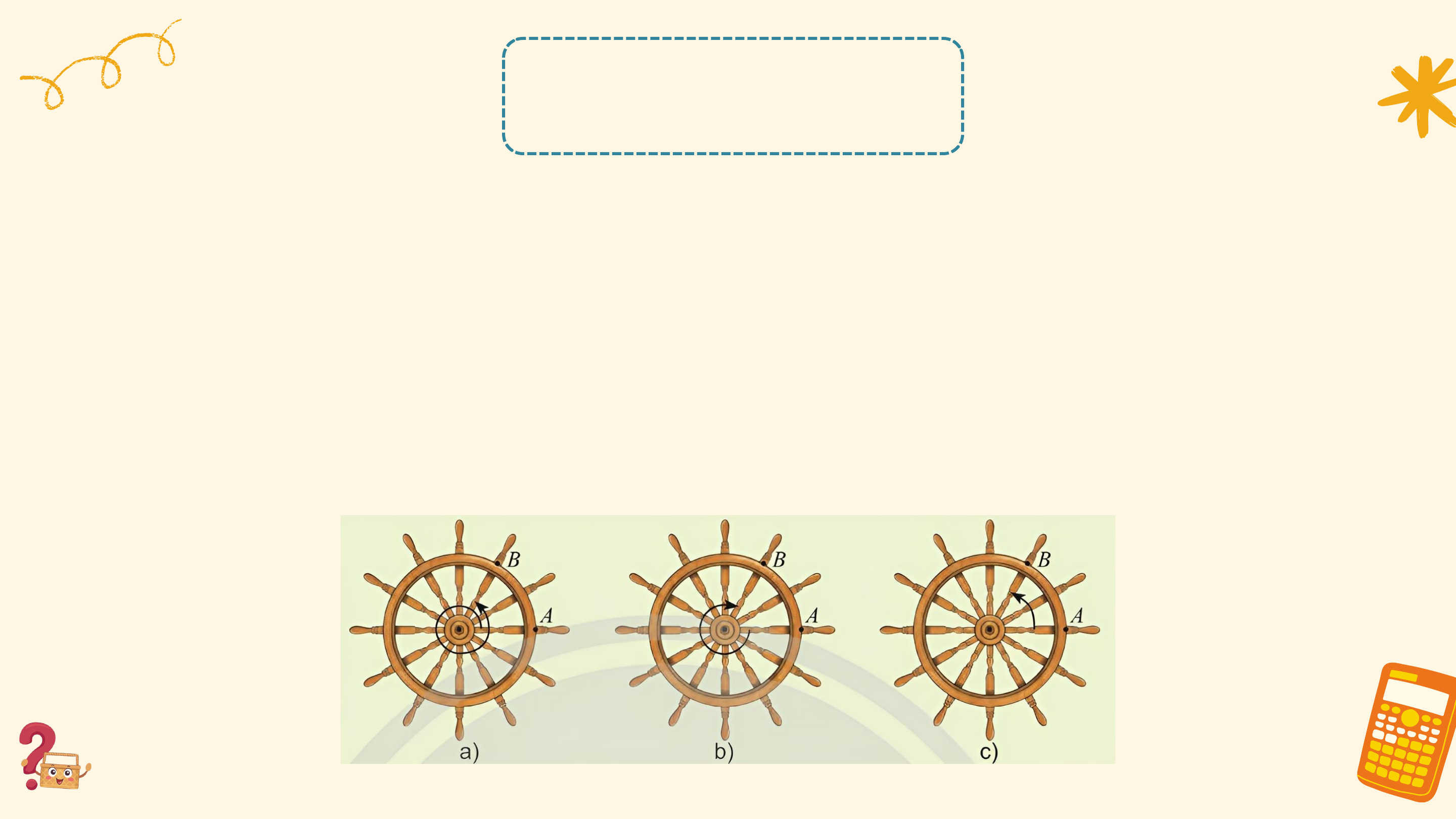
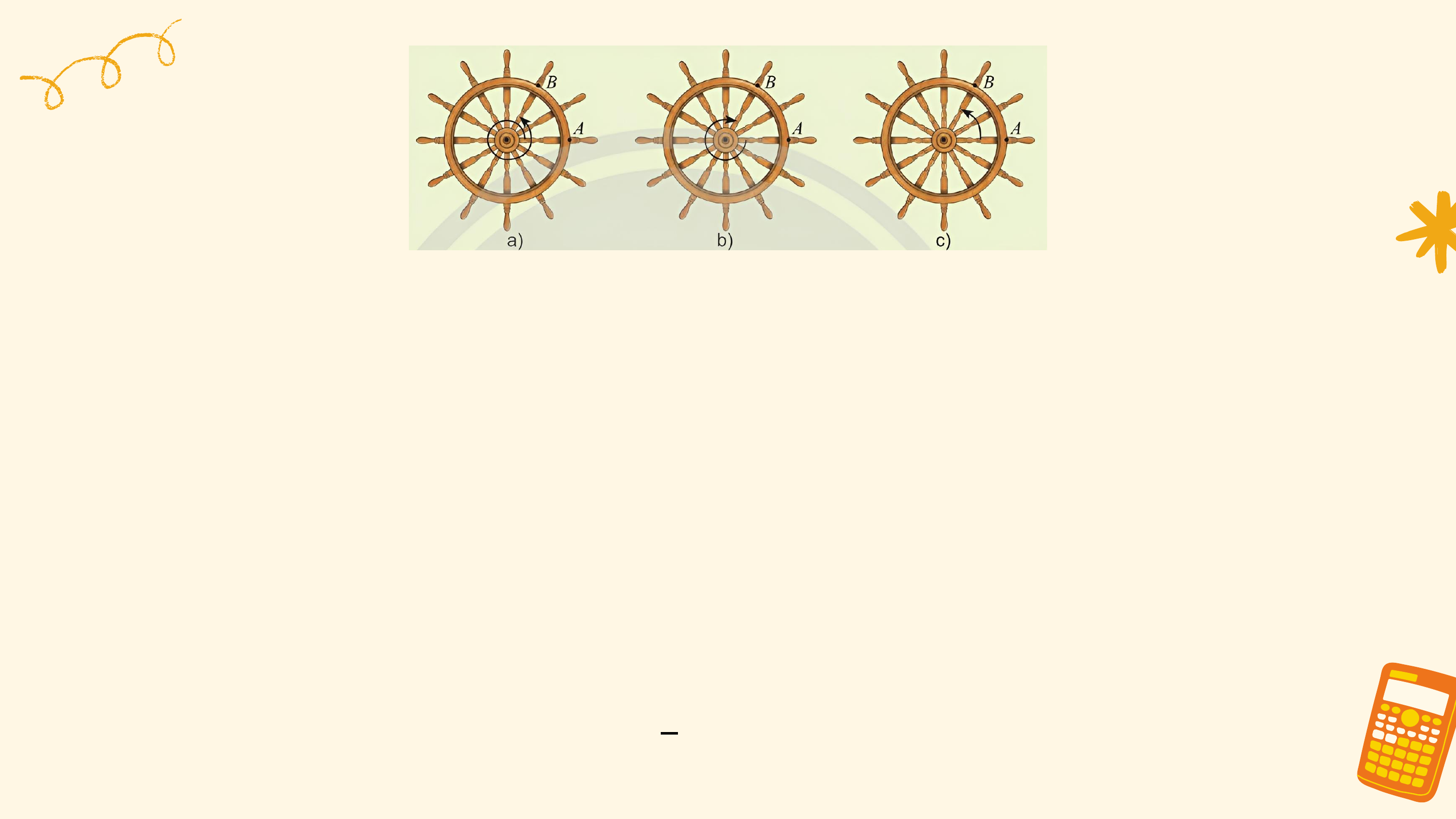
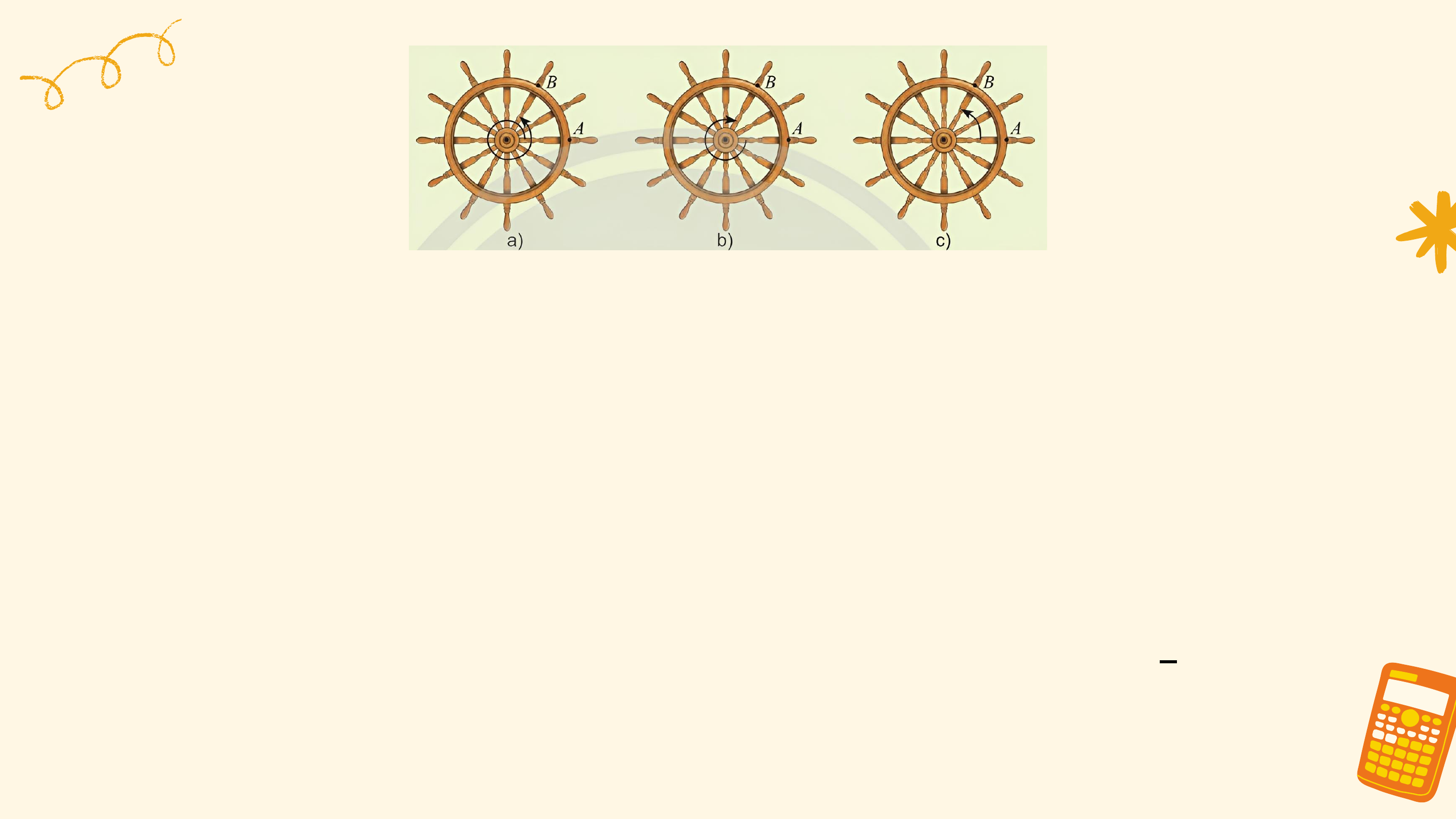
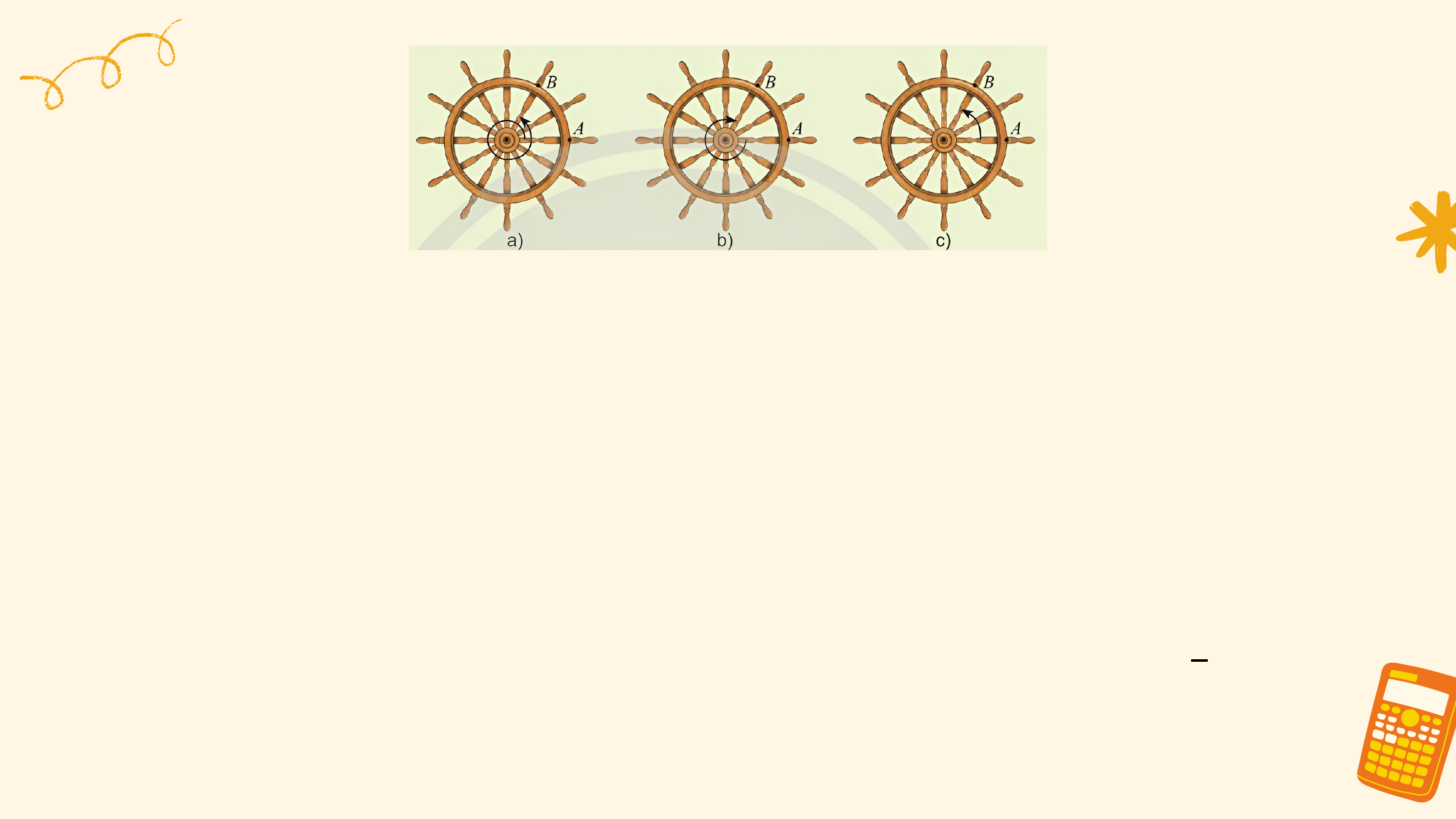
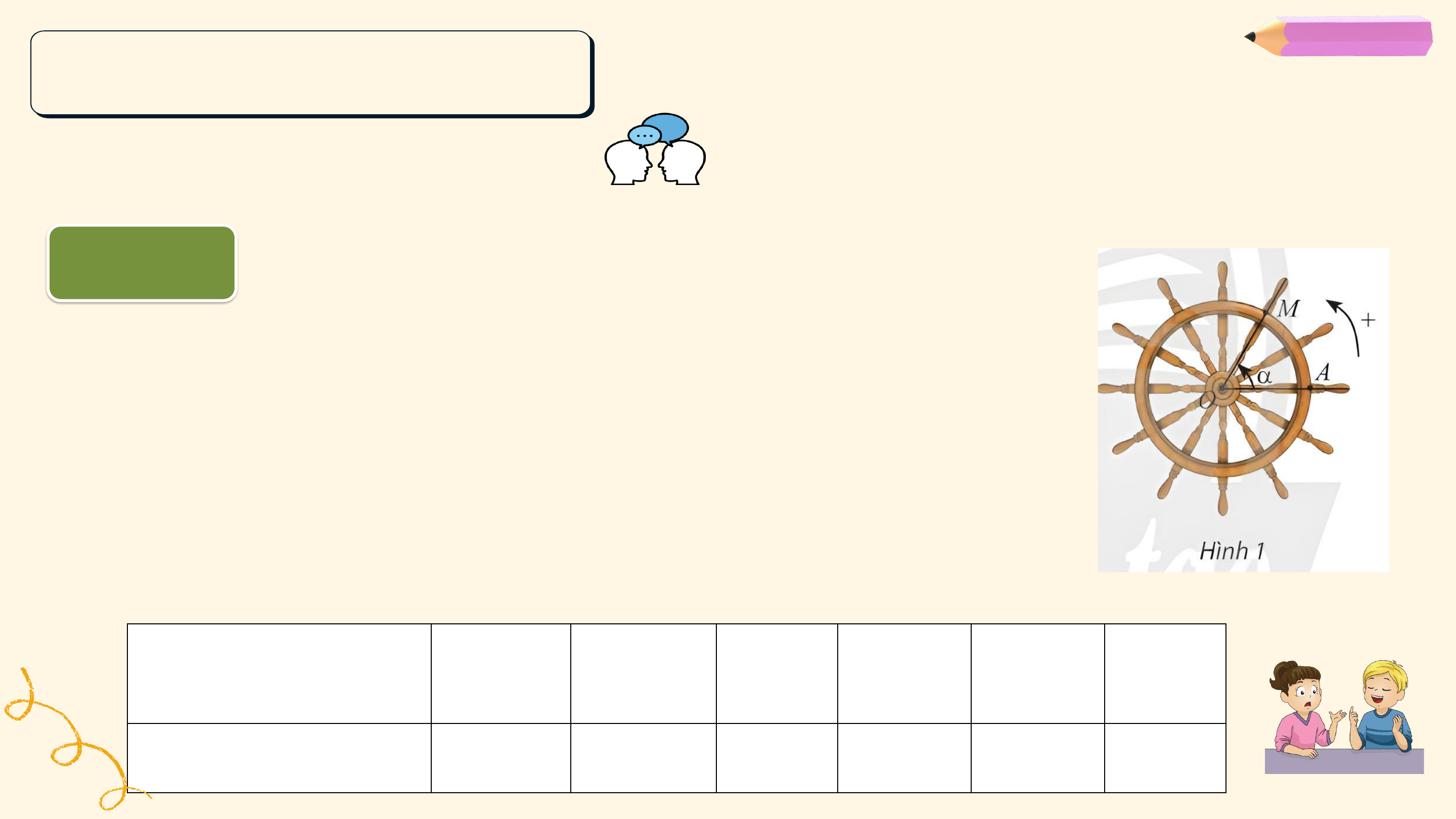
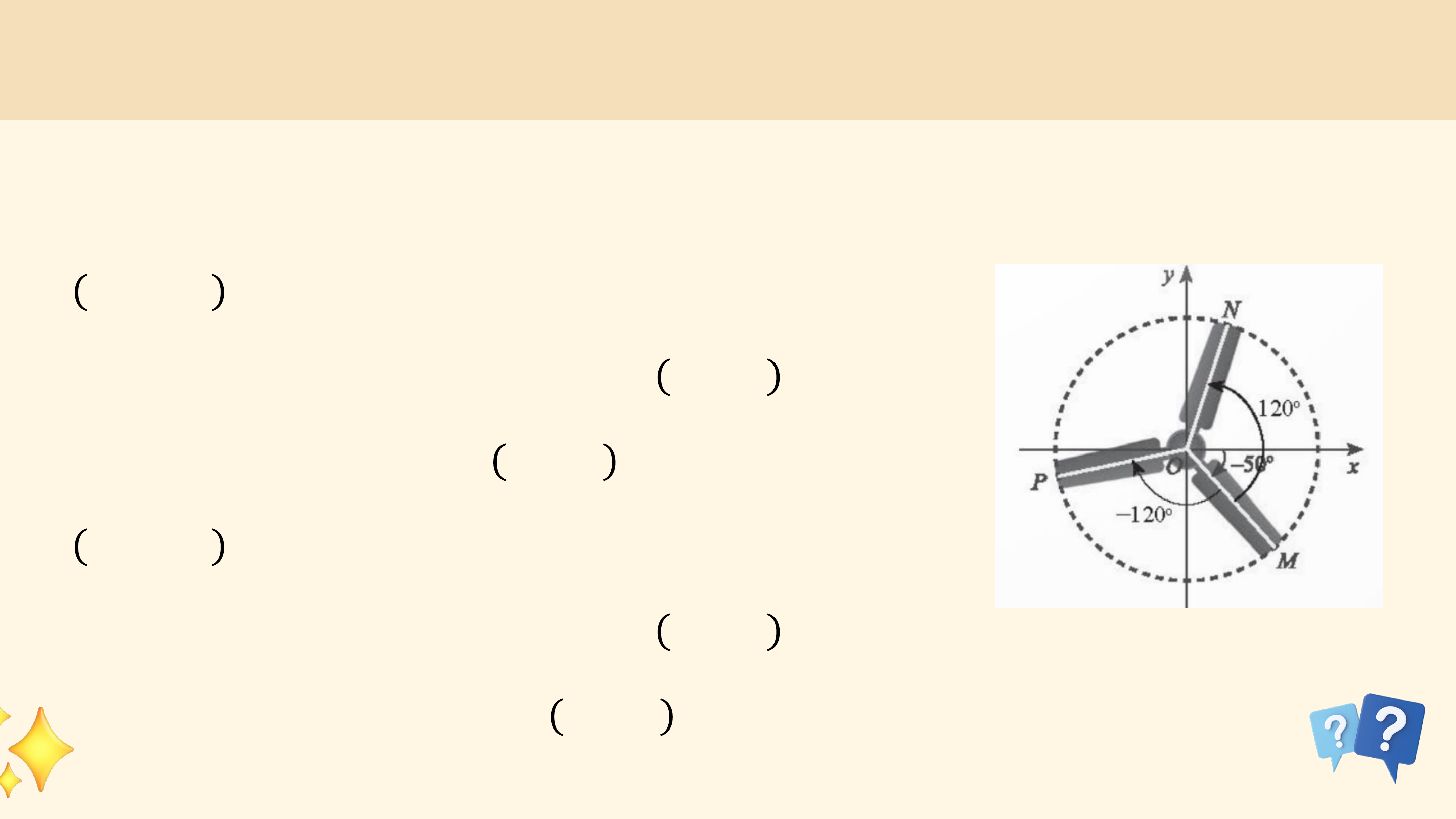
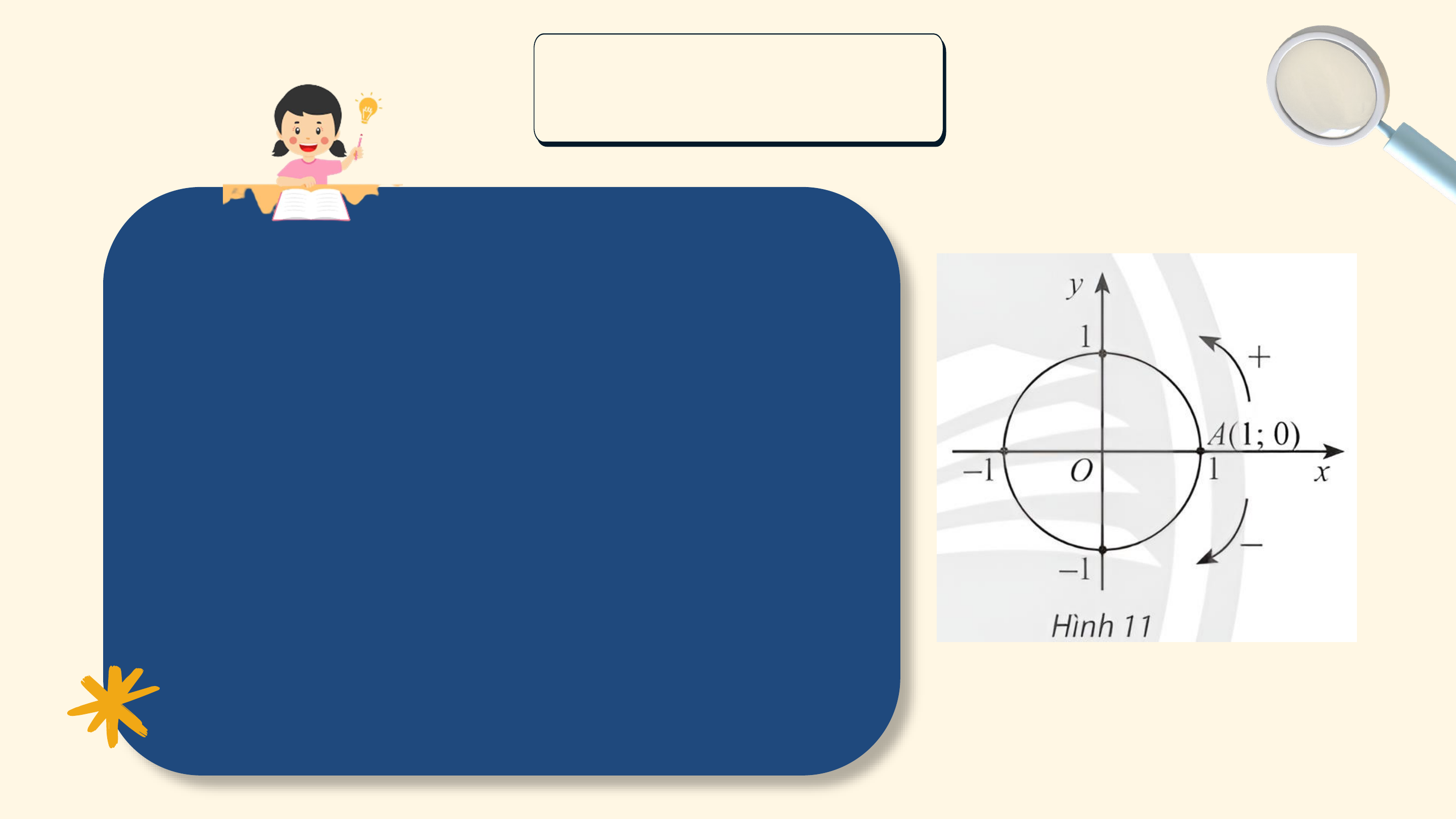
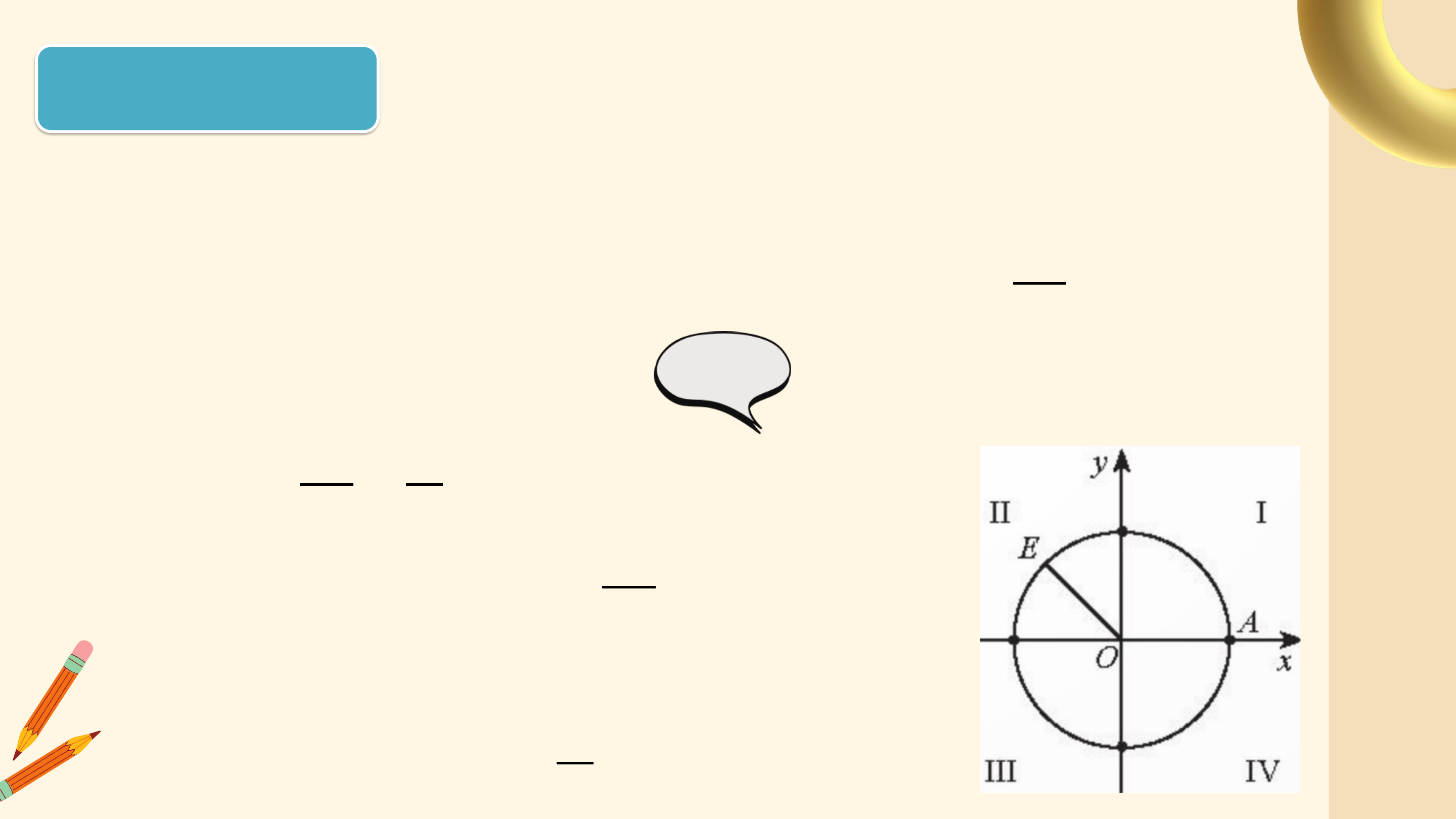
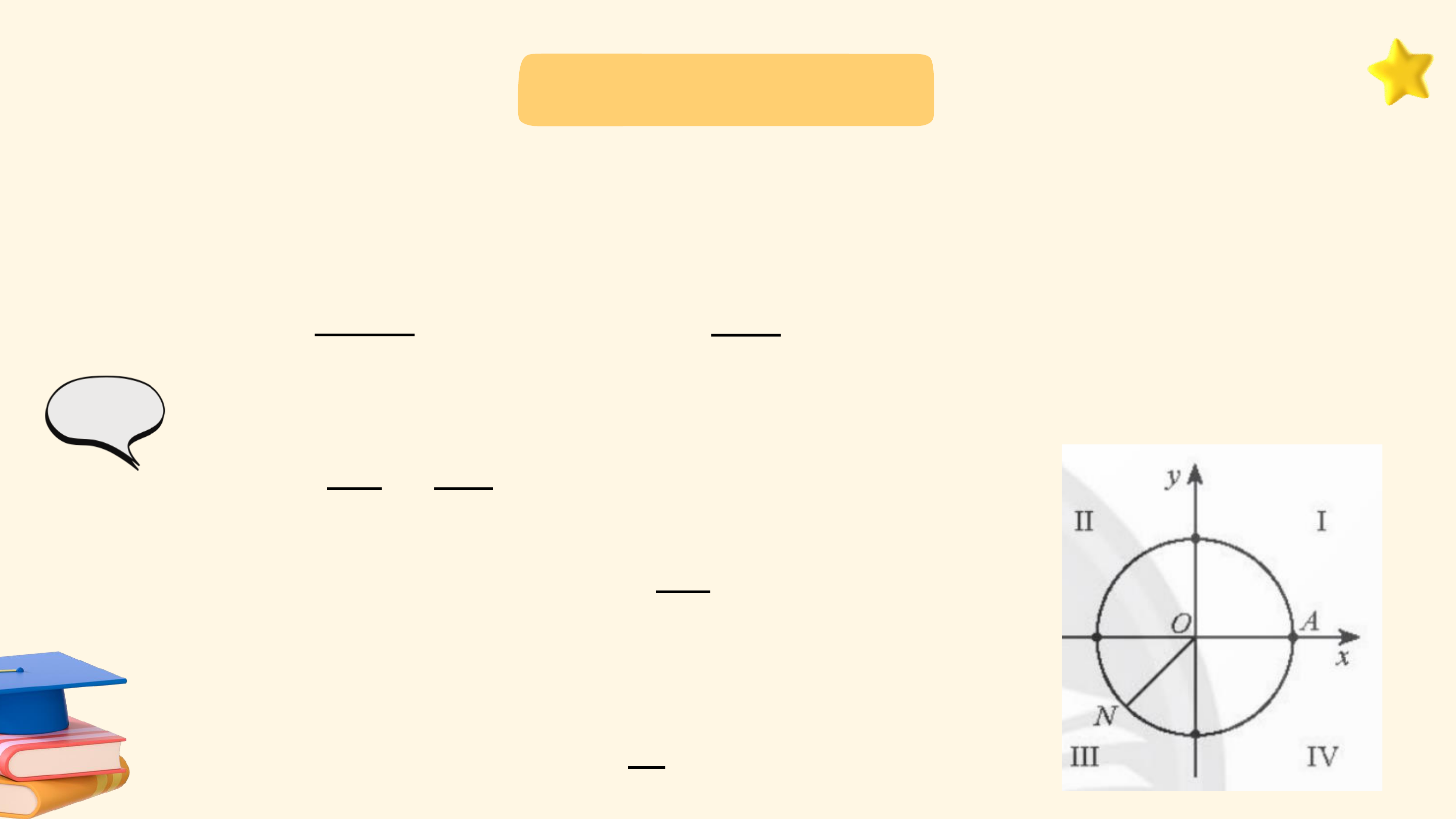
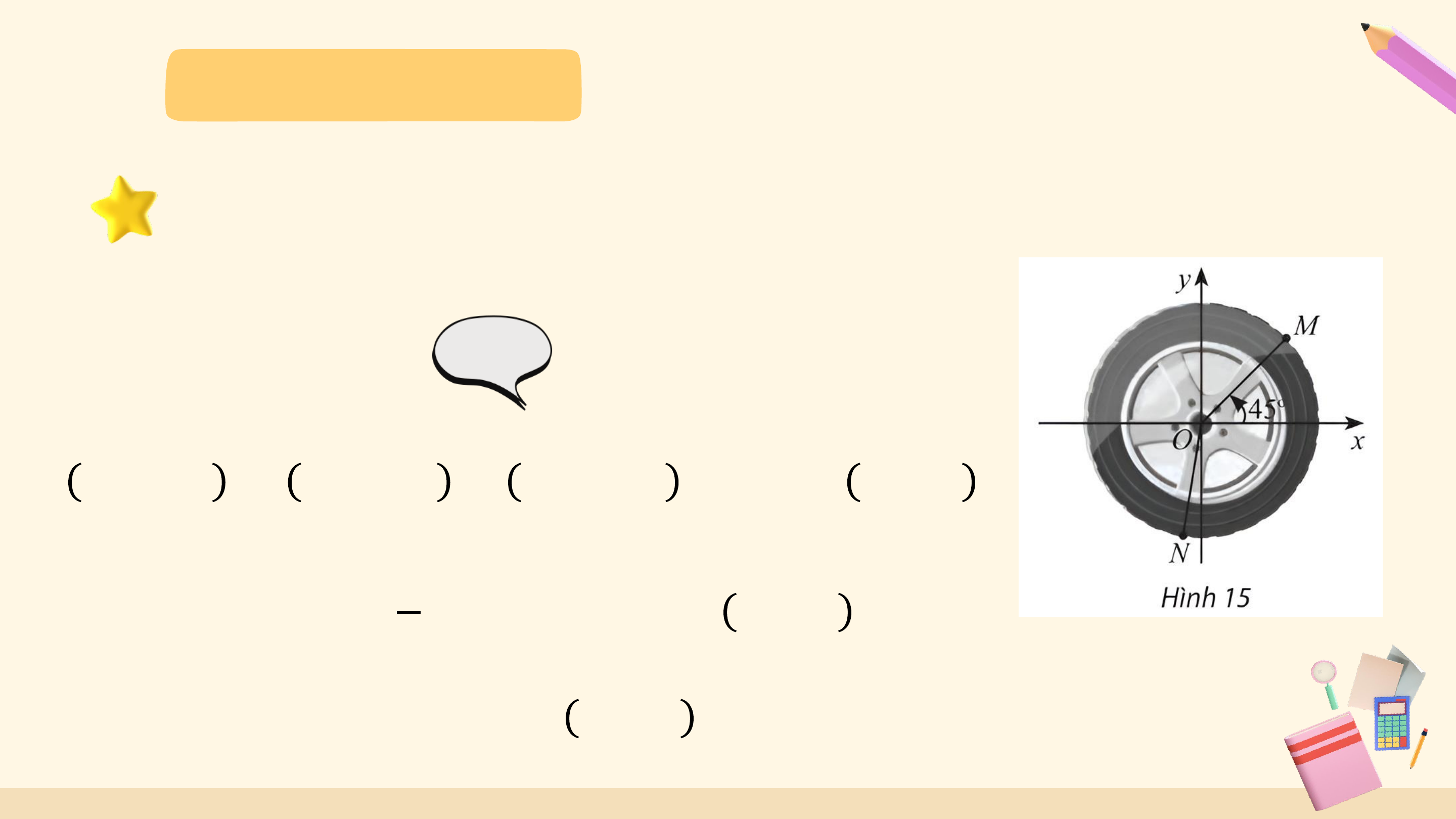
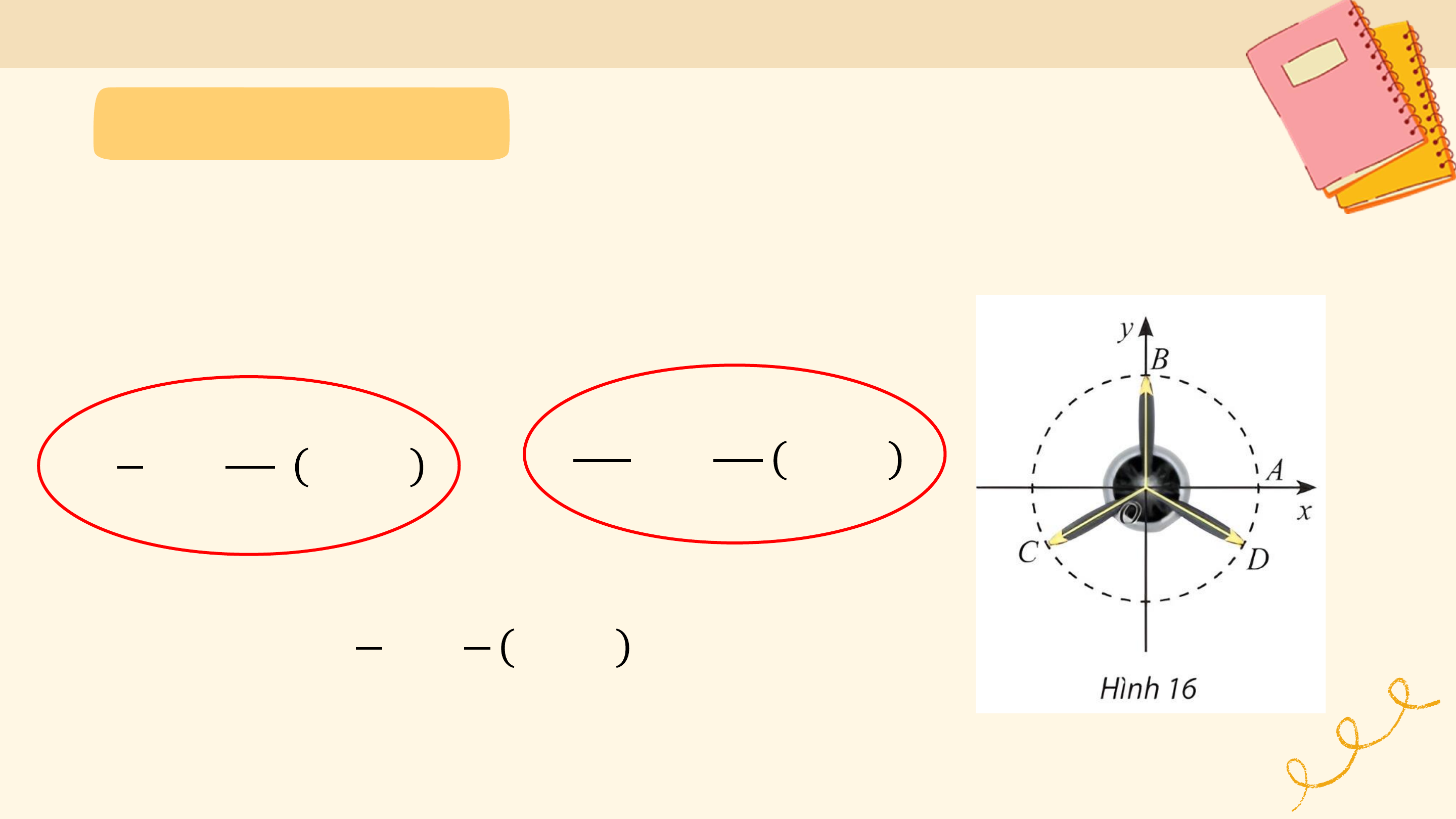
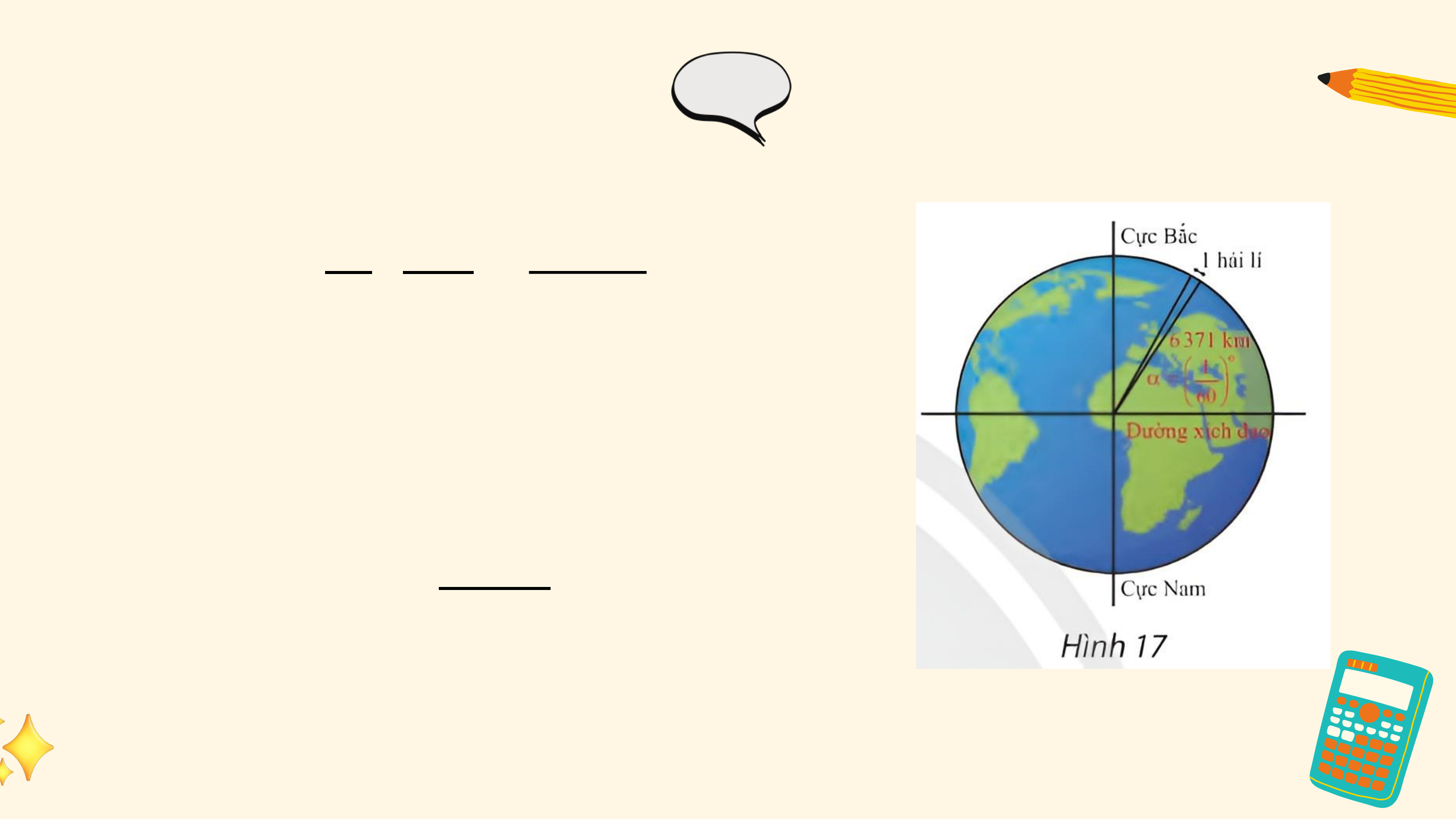
Mô hình dưới đây thể hiện chuyển động quay của một điểm trên
bánh lái tàu từ vị trí A đến vị trí B. Các chuyển động này có điểm nào
giống nhau, điểm nào khác nhau?
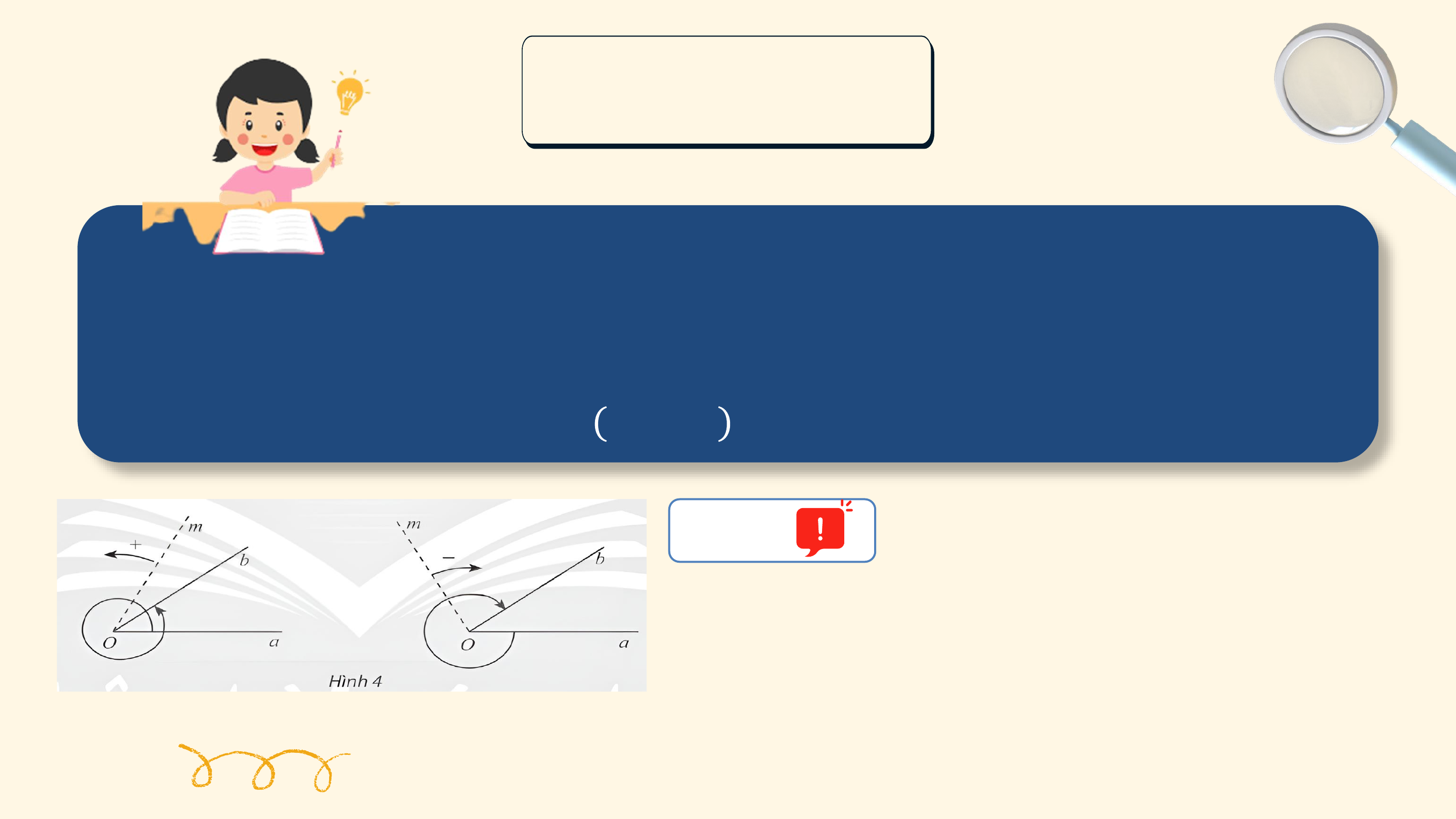
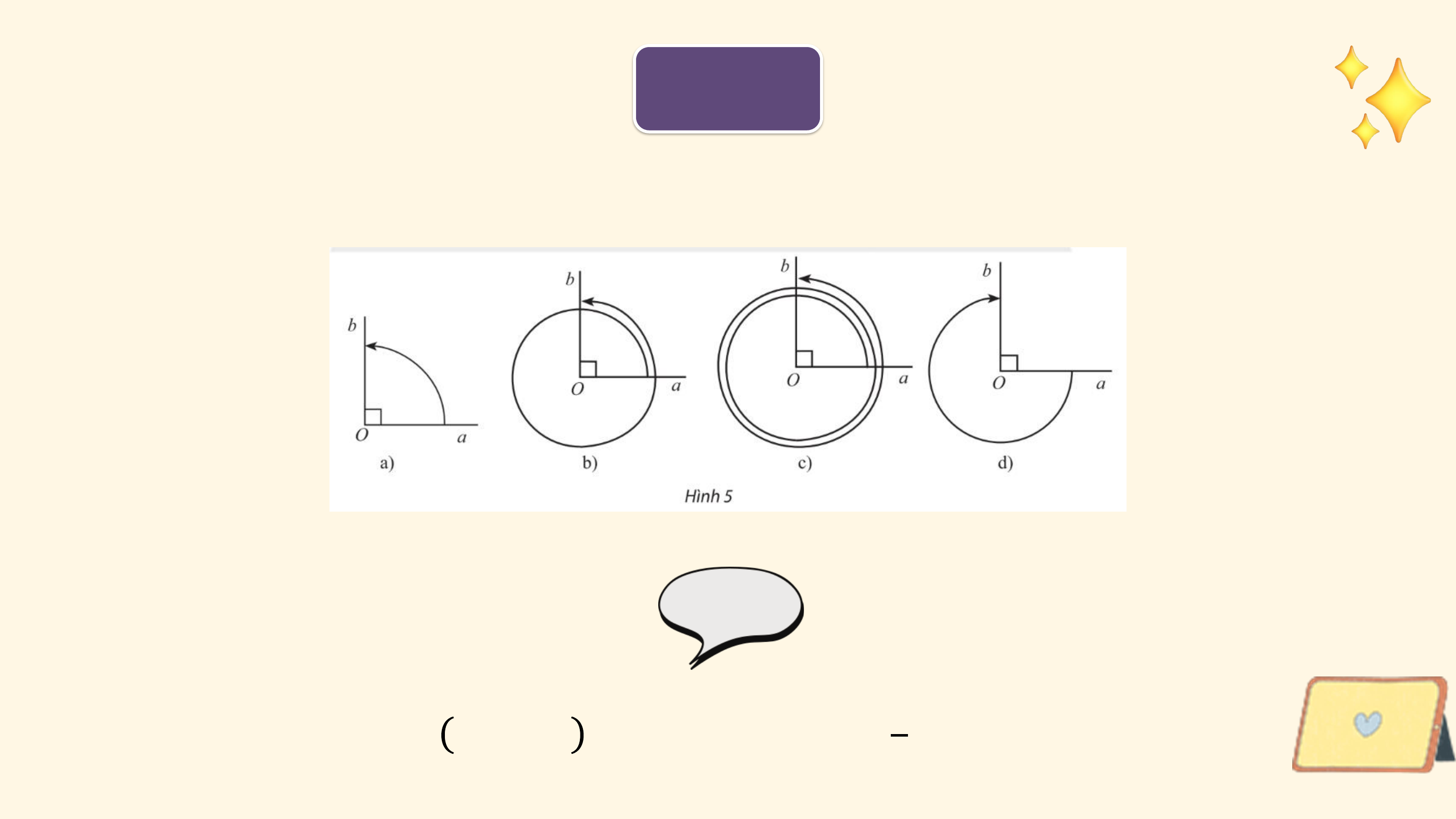
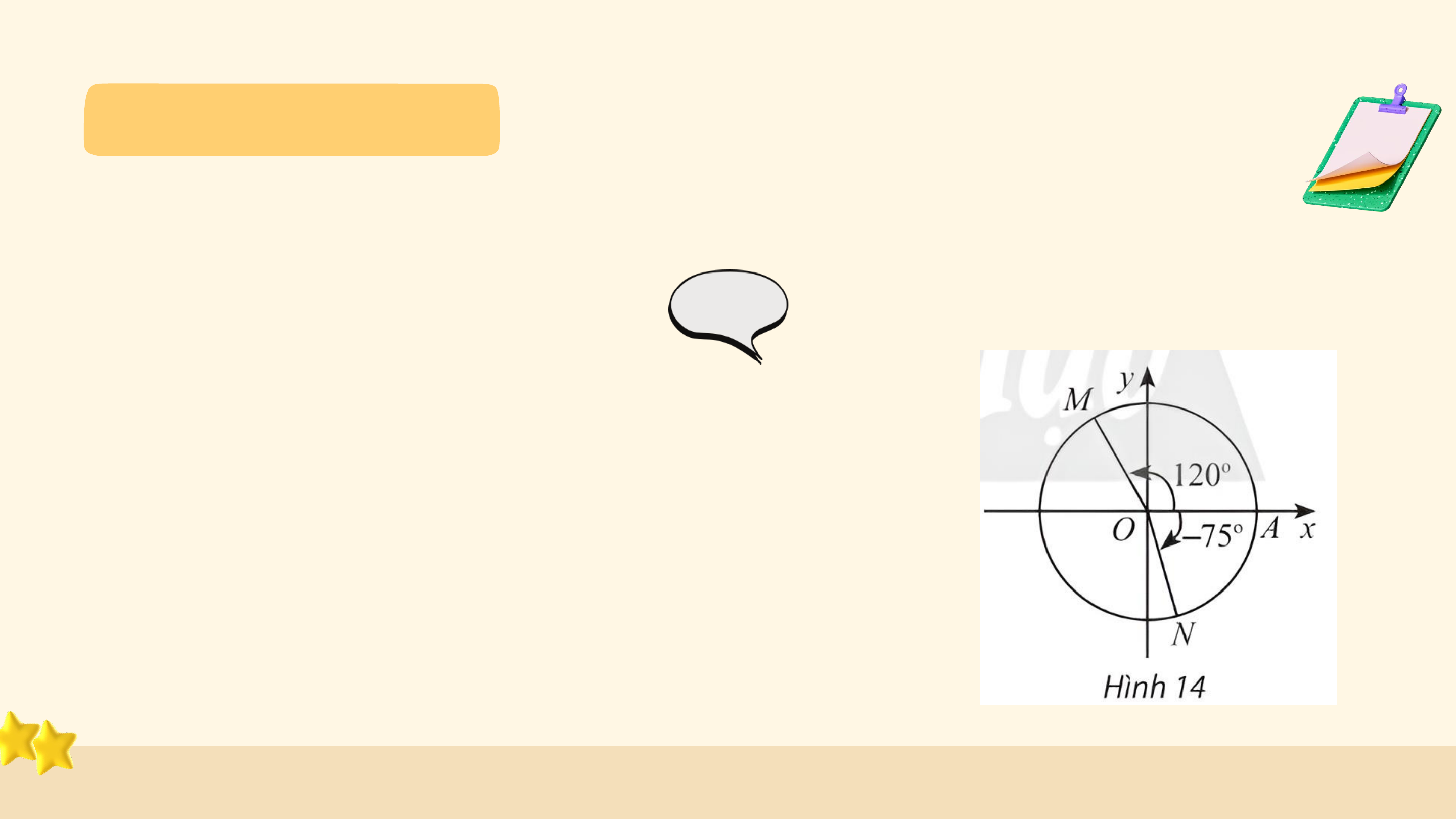
Các chuyển động có cùng điểm đầu là ? và điểm cuối là ?, mỗi
chuyển động quay theo một chiều cố định, tuy nhiên số vòng quay và chiều quay không như nhau:
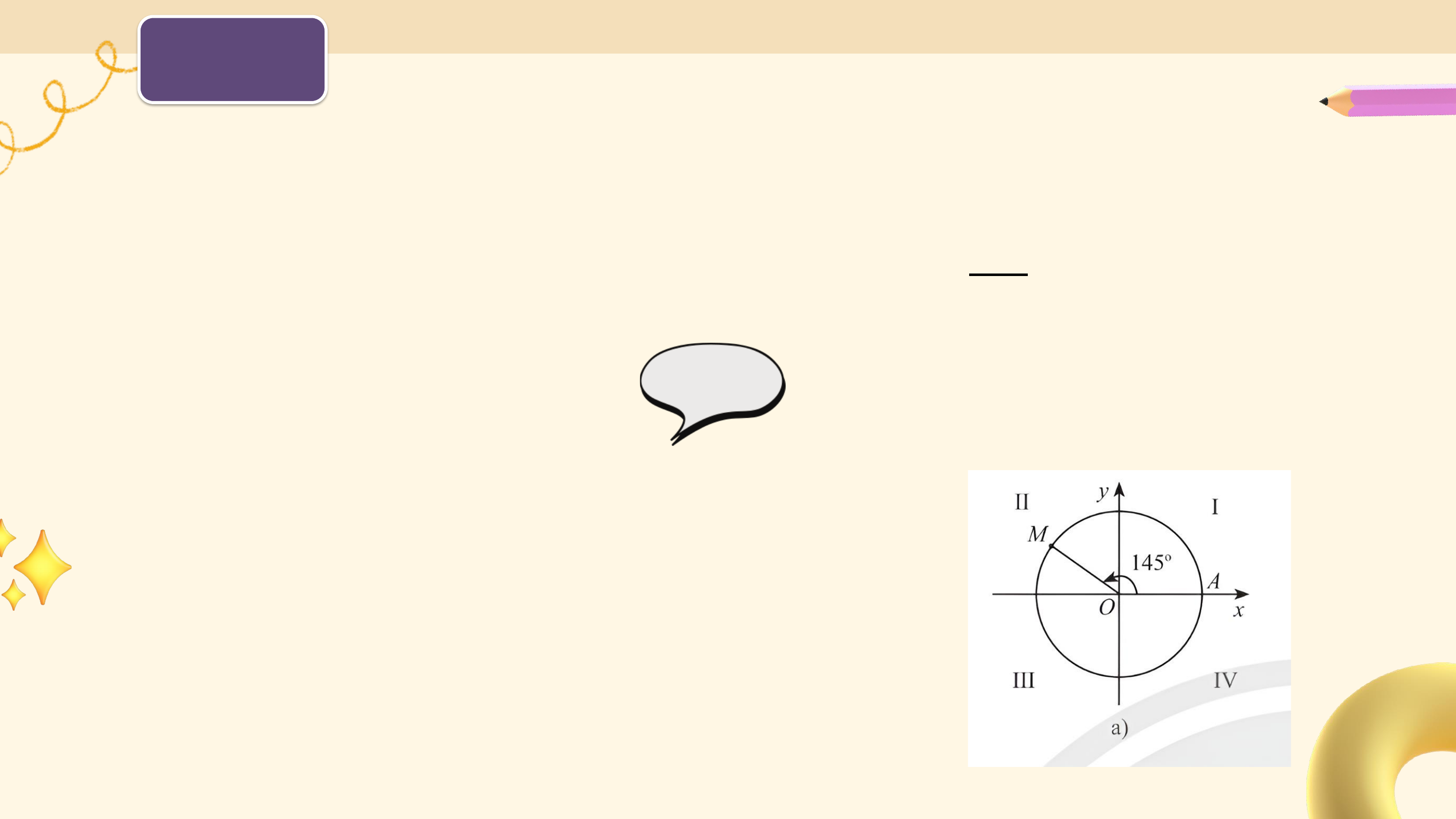
• Trong trường hợp a, bánh lái quay ngược chiều kim đồng hồ từ ?
đến ? sau đó quay thêm một vòng để gặp ? lần thứ 2 (quay ngược 1
chiều kim đồng hồ 1 vòng). 6
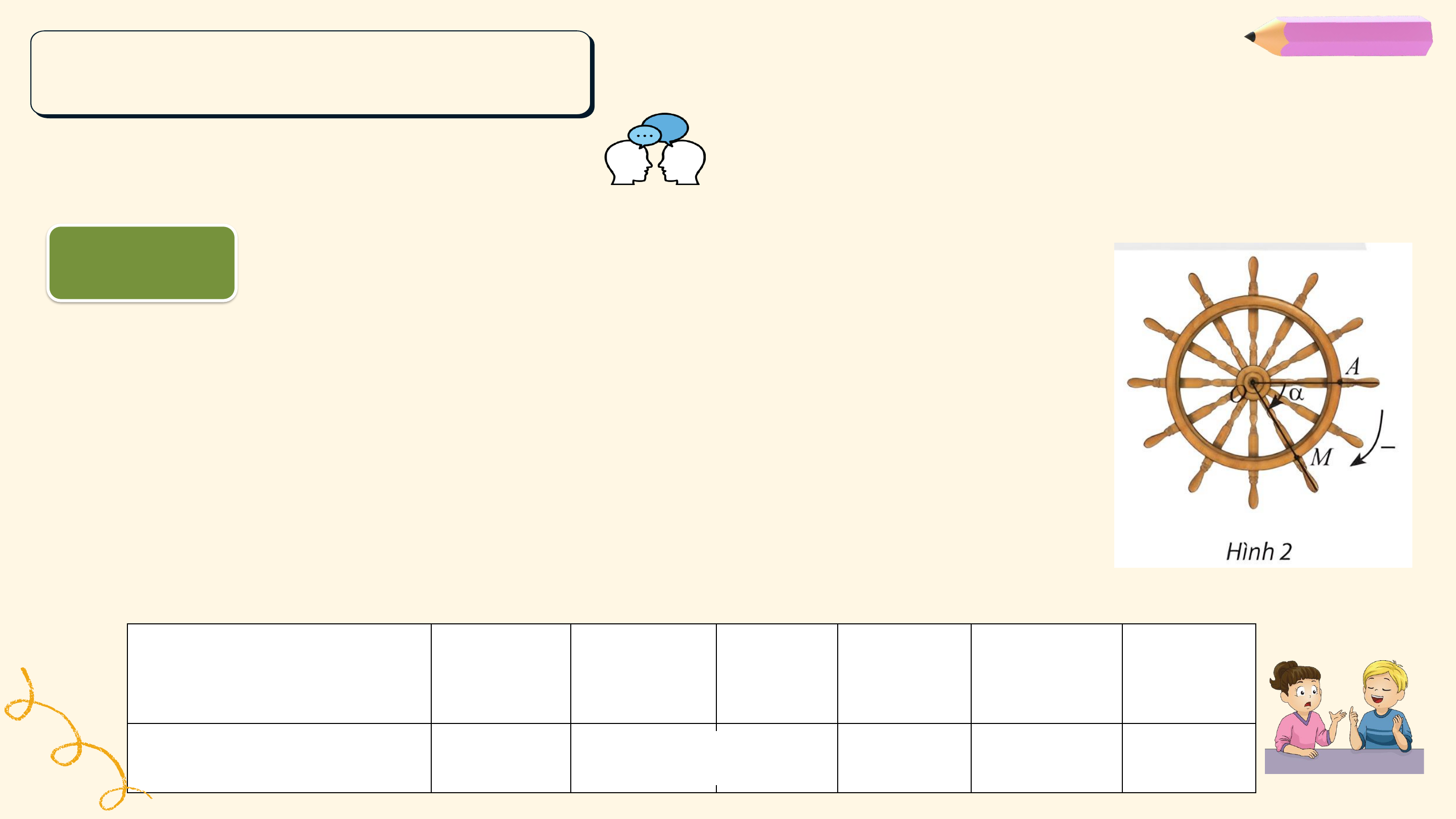
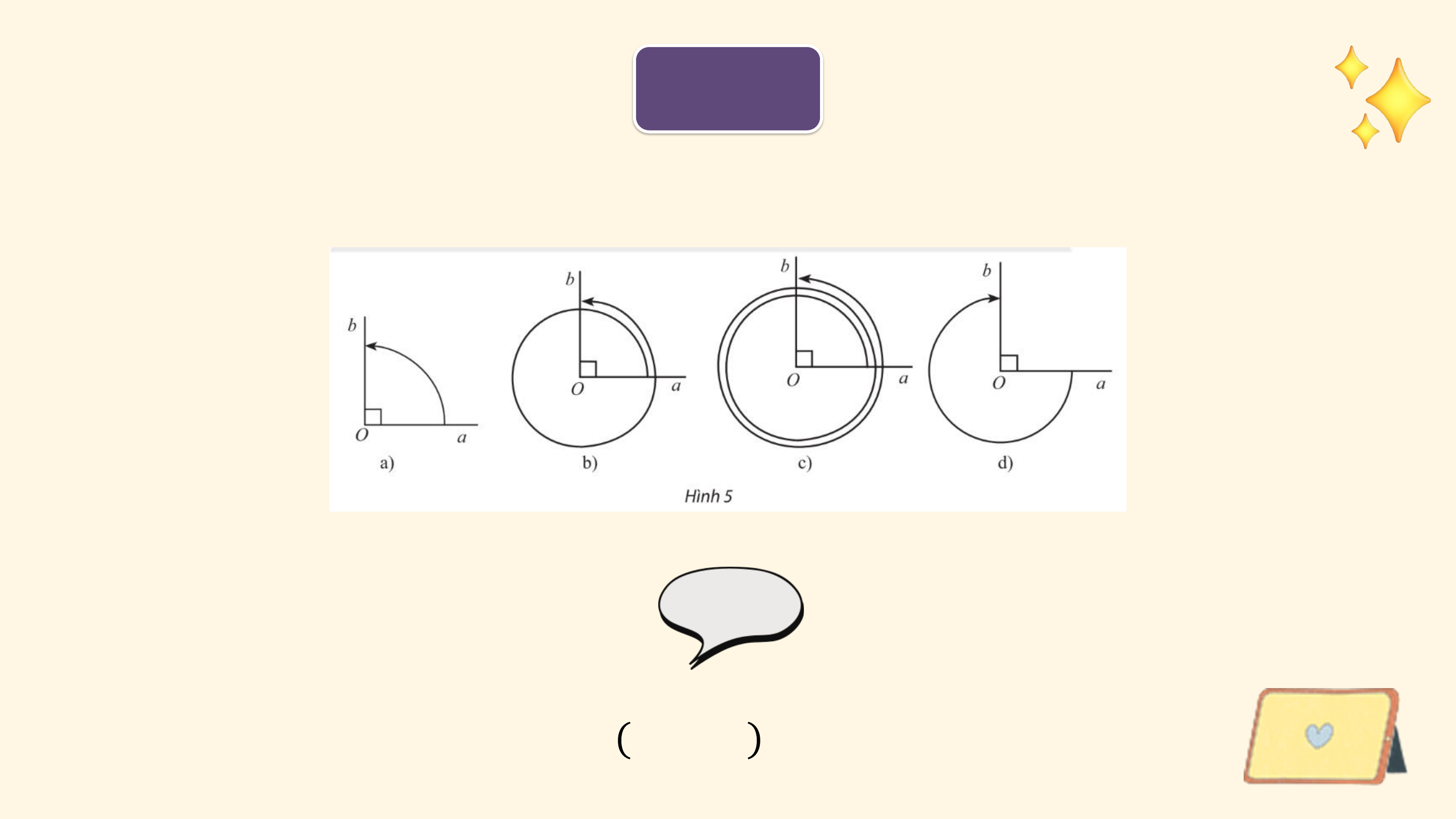
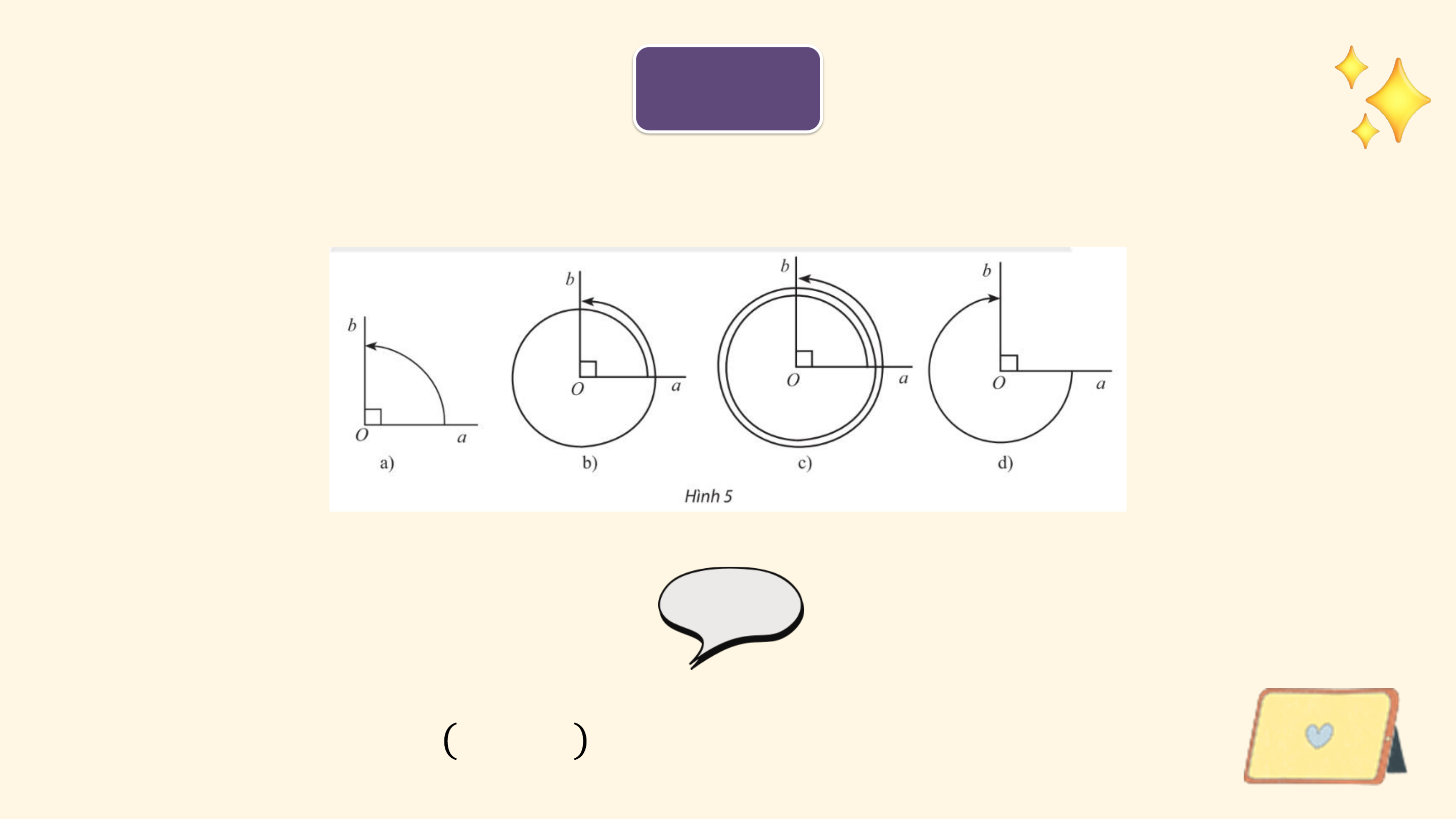
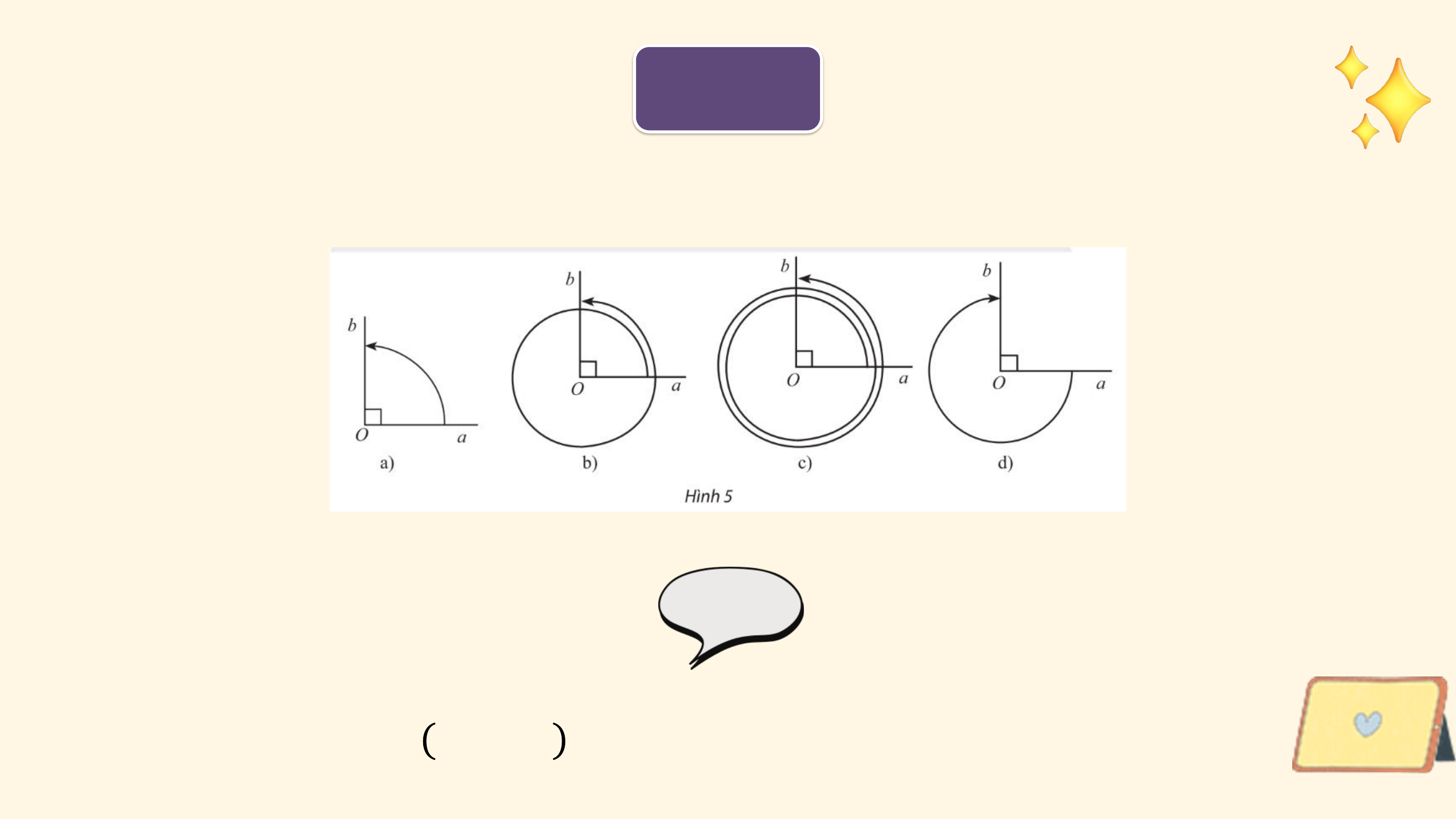
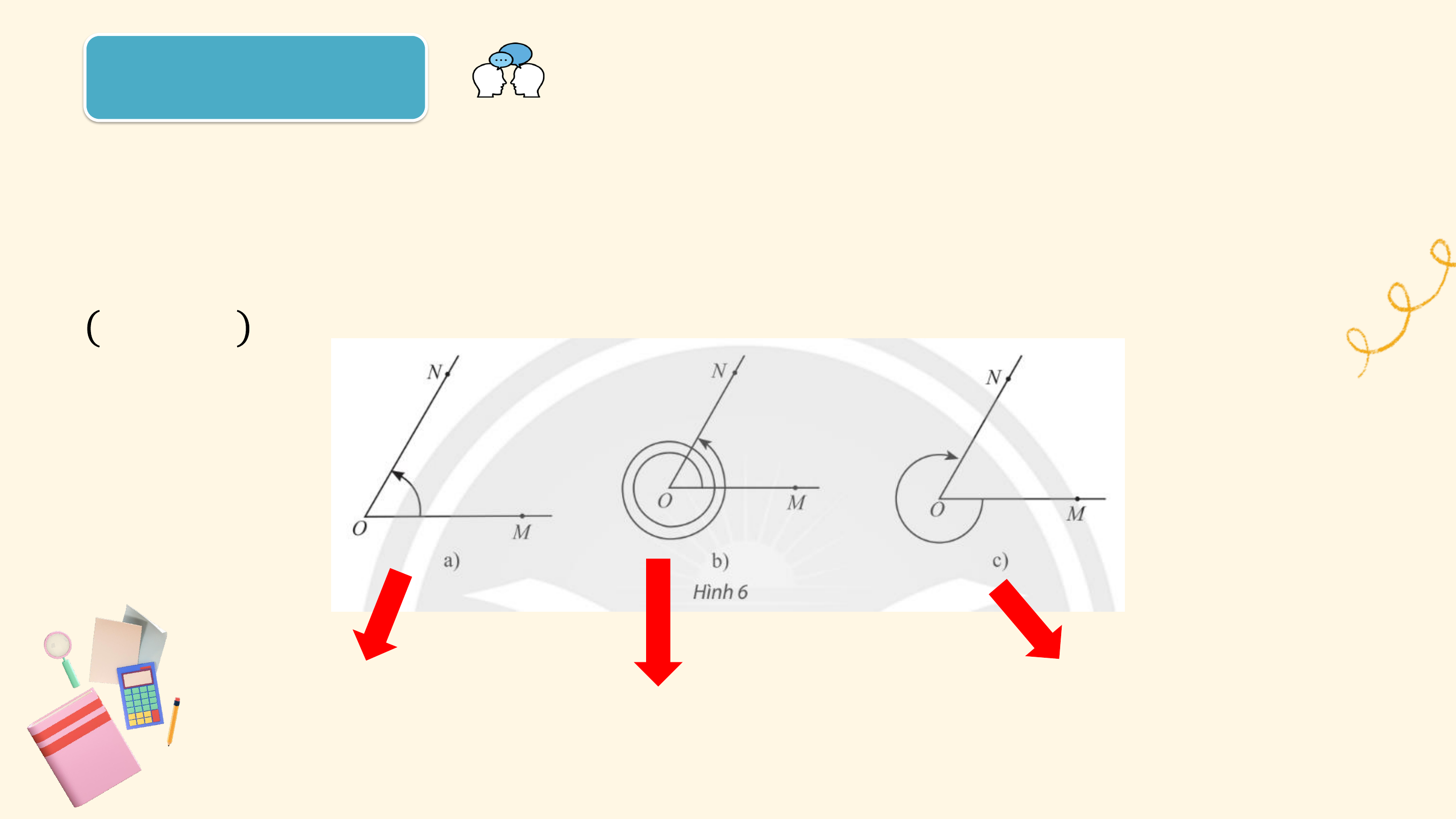
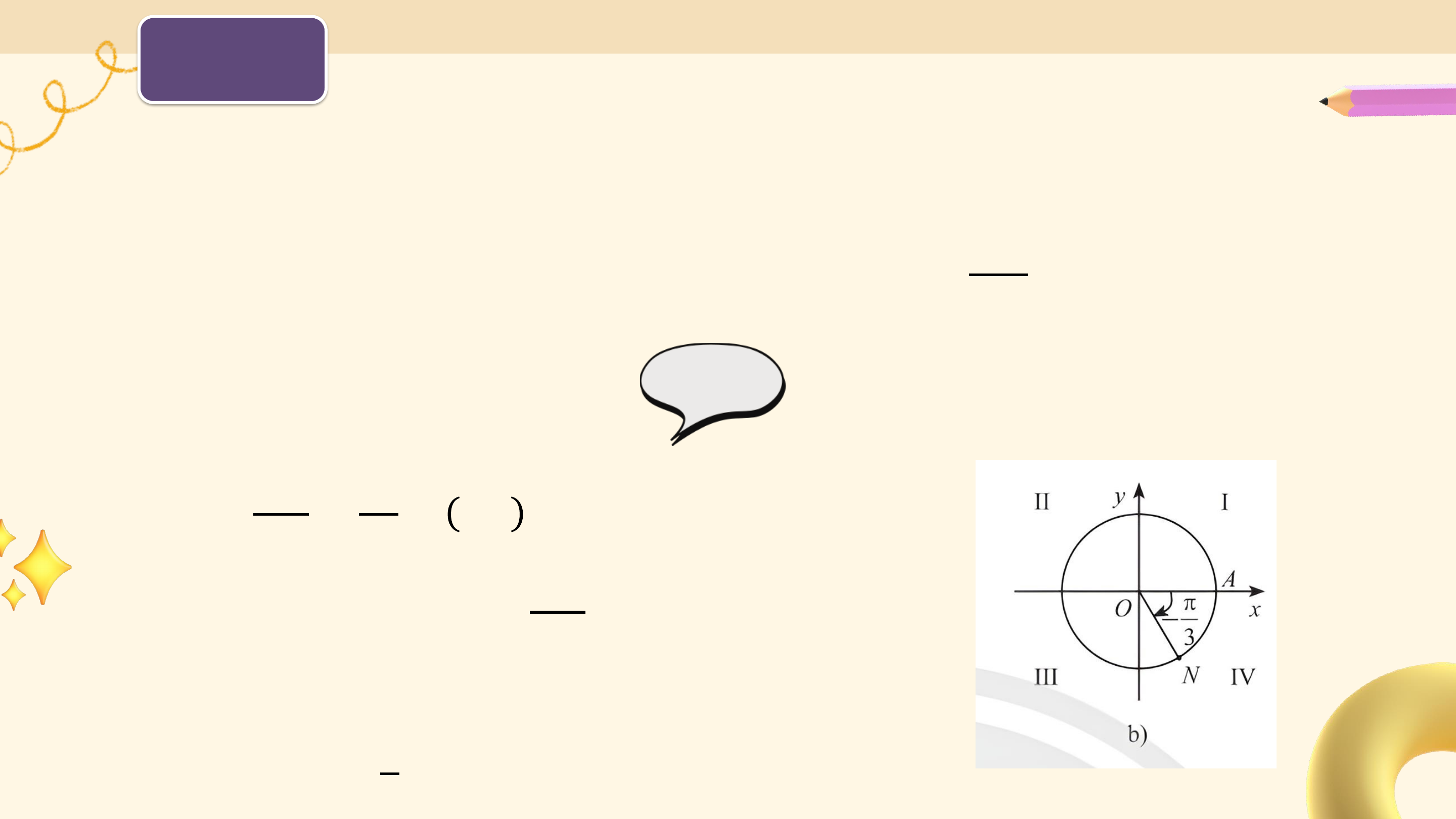
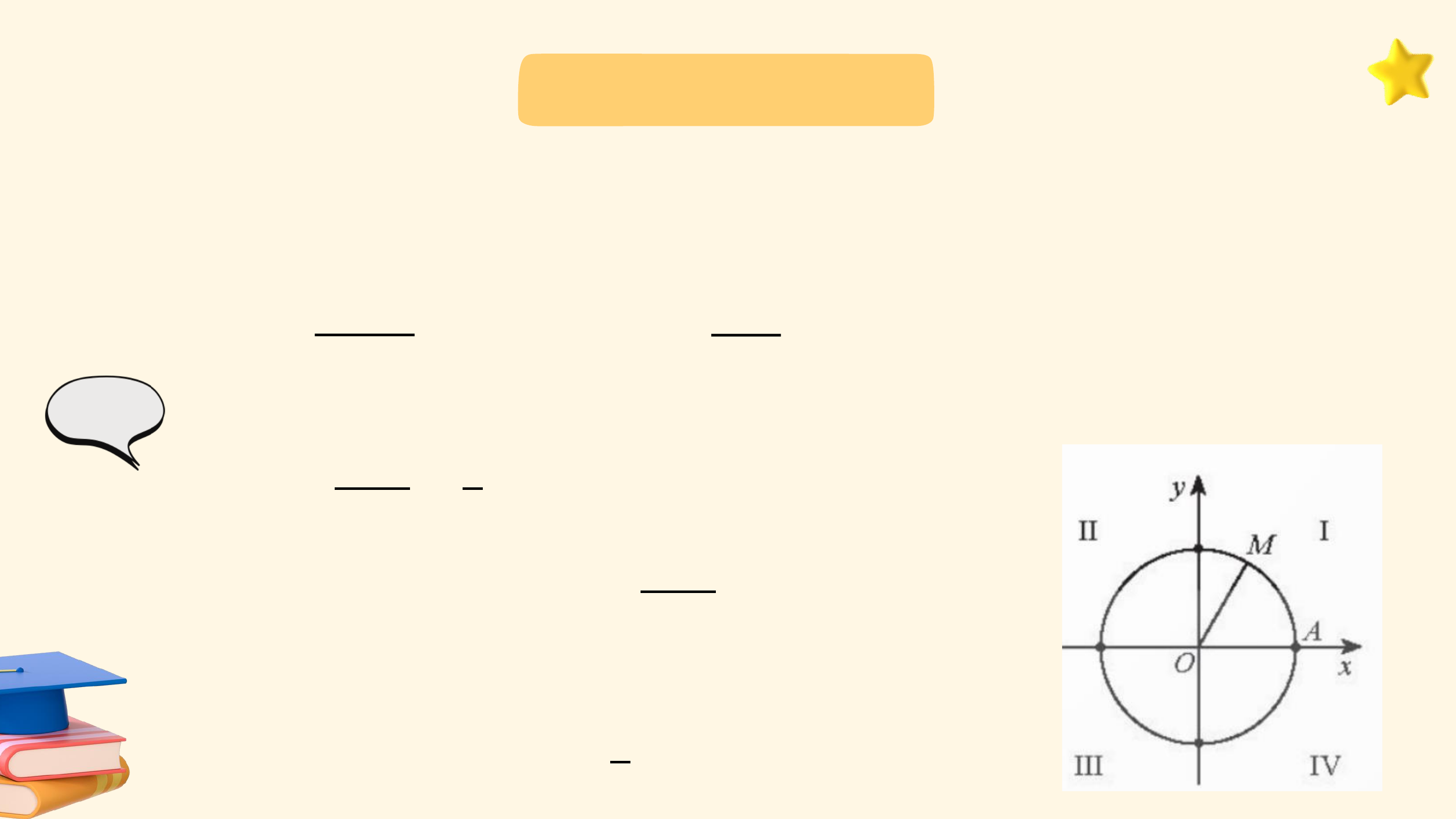
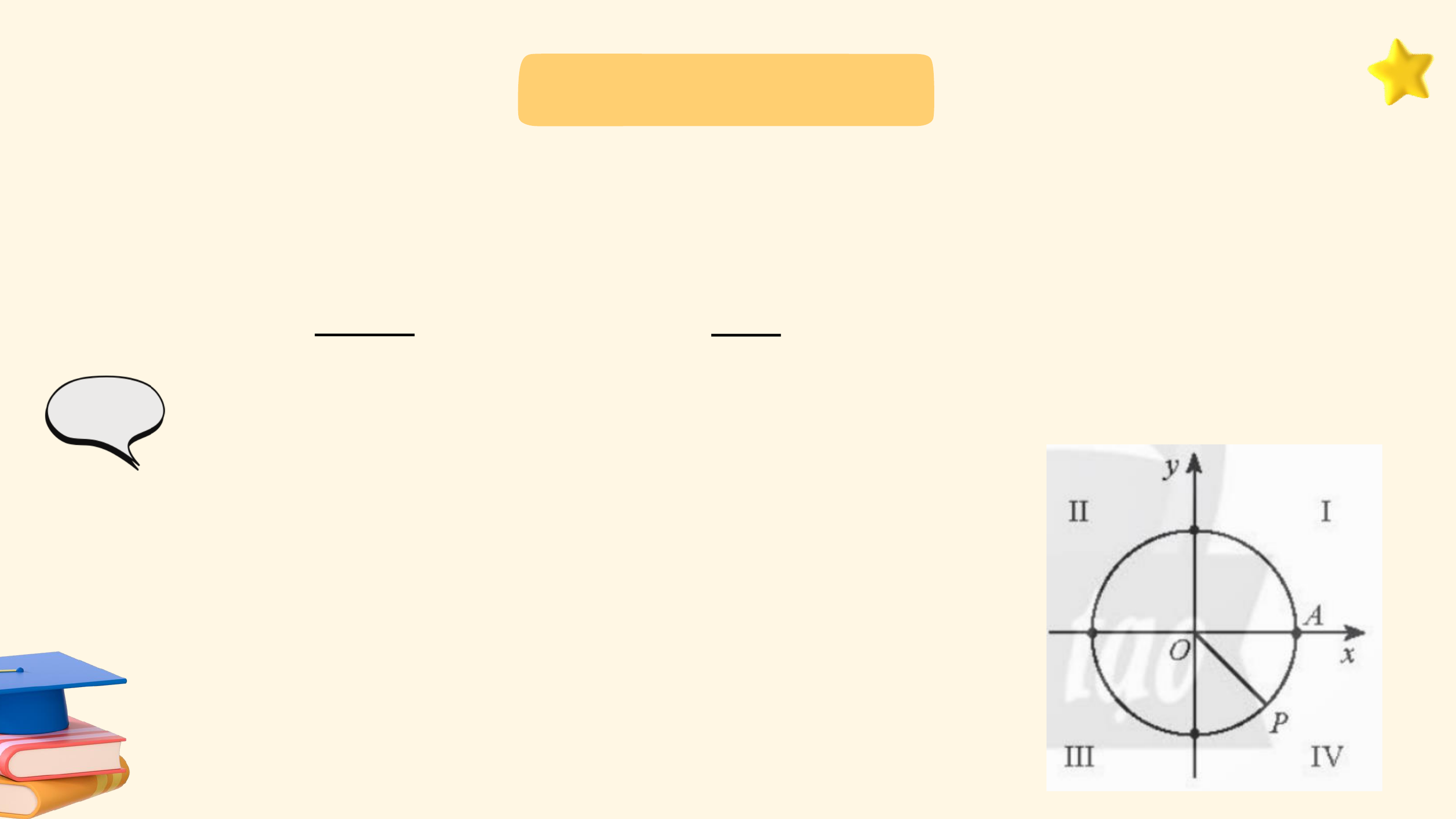
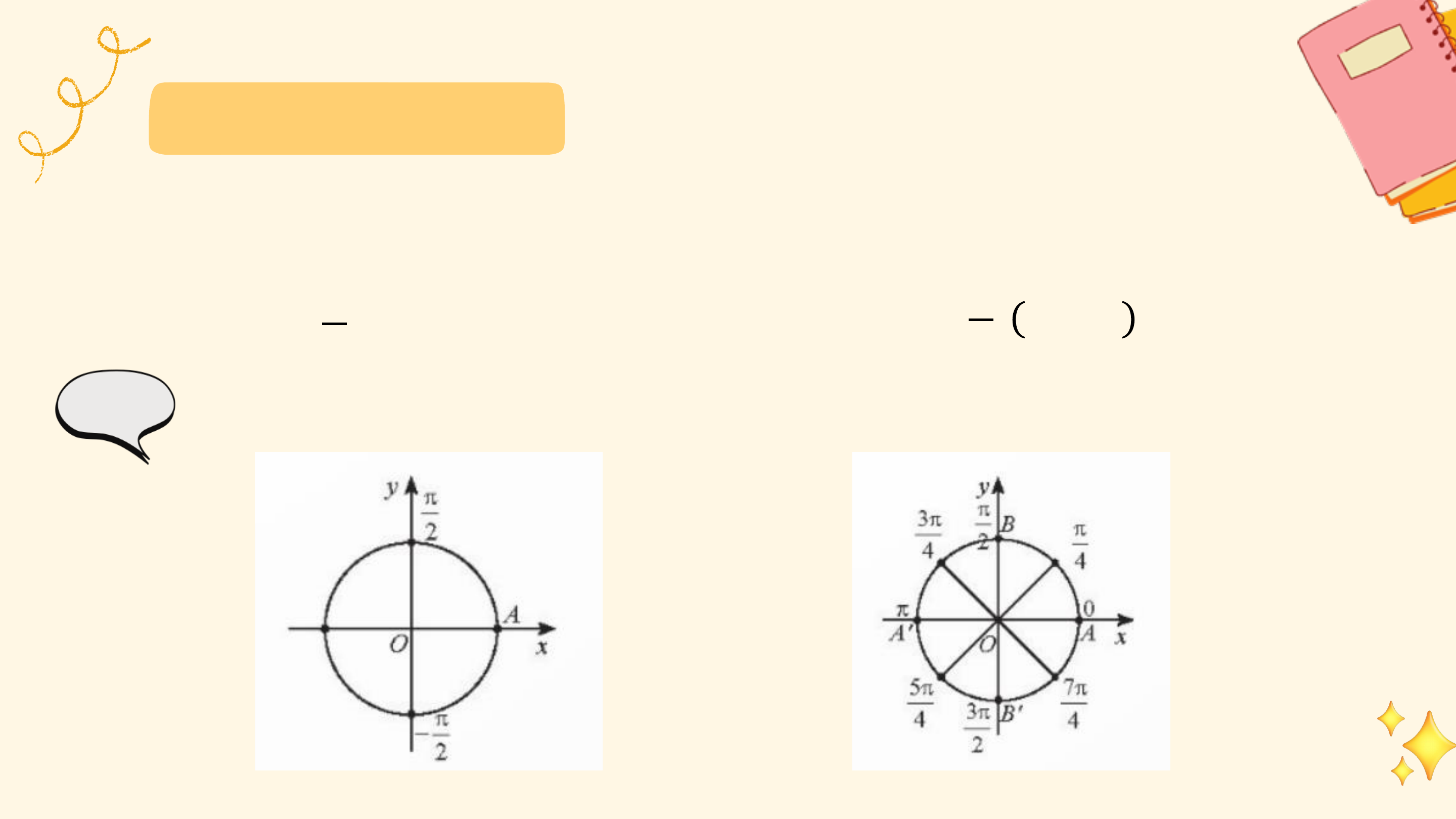
Các chuyển động có cùng điểm đầu là ? và điểm cuối là ?, mỗi
chuyển động quay theo một chiều cố định, tuy nhiên số vòng quay và chiều quay không như nhau:
• Trong trường hợp b, bánh lái quay cùng chiều kim đồng hồ từ ?
đến ?, gặp ? đúng 1 lần (quay cùng chiều kim đồng hồ 5 vòng). 6
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64