CHUYÊN ĐỀ 18:
CÁC BÀI TOÁN LIÊN QUAN ĐẾN PHÂN SỐ A- LÝ THUYẾT
I – Kiến thức cần nhớ 1. Phân số:
Với a là một số tự nhiên và b là một số tự nhiên khác 0, số có dạng a gọi là b
phân số (đọc là: a phần b)
a gọi là: tử số (số phần lấy ra)
b gọi là: mẫu số (số phần bằng nhau được chia trong một đơn vị) Ví dụ: 12 36 7 9 ; ; ; ... là các phân số 25 42 158 5
Một số tự nhiên a chia cho số tự nhiên b (b 0) có kết quả chính là phân số a b a a : b = b Ví dụ: 5 : 12 5 = 12
Như vậy ta xem dấu “gạch ngang: của phân số như là dấu chia.
Ta có thể dùng phân số để ghi kết quả của phép chia một số tự nhiên cho một số
tự nhiên (Cho dù phép chia đó là phép chia hết hay phép chia có dư)
Một số tự nhiên có thể viết dưới dạng phân số có mẫu số là 1: a a = 1
2. Một số tính chất cơ bản của phân số
Nếu ta nhân hay chia tử số và mẫu số của một phân số cùng với một số tự nhiên
khác 0 thì ta được một phân số mới bằng phân số đã cho a a m a : n = = m n ) b b (với 0, 0 m b : n Ví dụ: 18 18 2 36 18 : 3 6 = = = = 36 36 2 72 36 : 3 12
3. Phân số tối giản
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào khác 1. Ví dụ: 1 15 27 ; ; ;... 3 17 29
4. Rút gọn phân số
Muốn rút gọn phân số ta chia cả tử số và mẫu số của phân số đó với cùng một
số tự nhiên lớn hơn 1 mà tử số và mẫu số của phân số đó cùng chia hết cho số đó, để
được phân số mới có tử số và mẫu số nhỏ hơn tử số và mẫu số ban đầu và có giá trị bằng phân số ban đầu. Ví dụ: 15 15 :15 1 = = 60 60 :15 4 Chú ý:
- Phân số tối giản không thể rút gọn được
- Khi rút gọn phân số cố gắng rút gọn đến phân số tối giản
- Dựa vào dấu hiệu chia hết hoặc phép thử chọn để tìm được một số tự nhiên nào
đó lớn hơn 1 mà cả tử số và mẫu số của phân số đã cho đều chia hết cho số đó.
- Các Bước Rút Gọn Phân Số:
+ B1: Tìm số tự nhiên lớn hơn 1 mà cả tử số và mẫu số của phân số đã cho đều chia
hết. (Dấu hiệu chia hết)
+ B2: Tiến hành chia cả tử số và mẫu số của phân số cho số tự nhiên đã tìm được ở bước 1.
+ Lặp lại bước 1, 2 cho đến khi được phân số tối giản.
Ví Dụ : Rút gọn các phân số sau: 9 75 1414 201620162016 a) b) c) d) 18 115 2727 201720172017 Hướng dẫn 9 9 : 9 1 a) = = 18 18 : 9 2 75 75 : 5 15 b) = = 115 115 : 5 23 1414 1414 :101 14 c) = = 2727 2727 :101 27
Các phân số dạng ababab
... thì tử số và mẫu số sẽ chia hết cho các số: 101; 10101; cdcdcd
1001....Khi rút gọn được: ab ... cd 201620162016 201620162016 :100010001 2016 d) = = 201720172017 201720172017 :100010001 2017
5. Quy đồng phân số.
5.1. Quy Đồng Mẫu Số:
a) K/N: Quy đồng mẫu số là làm cho các phân số cần quy đồng có chung một mẫu số. b) Phương pháp:
Phương pháp 1: Lấy tử số và mẫu số của phân số này nhân với mẫu số của phân số kia.
Ví Dụ: Quy đồng mẫu số hai phân số sau: 3 4 và 4 7 Hướng dẫn 3 3 4 21 4 4 4 16 Ta có: = = = = 4 4 và 7 28 7 7 4 28
Vậy sau khi quy đồng mẫu số hai phân số 3 4 và
ta được hai phân số mới có cùng 4 7
mẫu số tương ứng là: 21 16 và 28 28
Phương pháp 2: Khi mà mẫu số của các phân số cùng chia hết cho một số tự nhiên lớn hơn 1.
B1: Tìm số tự nhiên lớn hơn 1 mà các mẫu số cùng chia hết.
B2: Tính tích các mẫu số.
B3: Chia tích vừa tìm được ở bước 2 cho số tự nhiên tìm được ở bước 1. Thì kết quả
tìm được sẽ là mẫu số chung cần tìm.
B4: Chia mẫu số chung cho các mẫu số được một số. Tiến hành nhân cả tử số và mẫu
số của phân số đó cho số vừa tìm được. 5
Ví dụ: Quy đồng mẫu số các phân số: 1 và 4 6 Hướng dẫn B1: Cùng chia hết cho 2.
B2: Tích các mẫu số: 4 6 = 24
B3: Mẫu số chung là: 24 : 2 = 12
B4: Ta có: 12 : 4 = 3 cần nhân cả tử và mẫu của 1 với 3. Cũng có: 12 : 6 = 2 cần nhân 4
cả tử và mẫu của 5 với 2. 6 Bài giải: 1 1 3 3 5 5 2 10 Ta có: = = = = 4 4 và 3 12 6 6 2 12
Sau khi quy đồng mẫu số hai phân số 1 5 và
ta được hai phân số cùng mẫu số tương 4 6 ứng là: 3 10 và 12 12
Phương pháp 3: Khi mà mẫu số của các phân số cùng chia hết cho một số tự nhiên lớn
hơn 1. Ta chọn ra mẫu số lớn nhất, nhân mẫu số đó lần lượt với 2, 3, 4... cho đến khi
được một số mà chia hết cho tất cả các mẫu số của các phân số còn lại thì số đó ta lấy làm mẫu số chung. 5
Ví dụ: Quy đồng mẫu số các phân số sau: 7 2 ; và 15 3 6
Phân tích: 15 là mẫu số lớn nhất. 15 chia hết cho 3. Thấy: 15 2 = 30 chia hết cho 6.
Suy ra: mẫu số chung là 30. Hướng dẫn 7 7 2 14 2 2 10 20 5 5 5 25 Ta có: = = ; = = = = 15 15 2 30 3 3 và 10 30 6 6 5 30
Vậy sau khi quy đồng mẫu số các phân số 7 2 5 ; và
ta được các phân số có cùng 15 3 6
mẫu số tương ứng là: 14 20 25 ; và 30 30 30
Chuyên đề Các bài toán liên quan đến phân số lớp 4 (có lời giải)
629
315 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Trọn bộ 24 Chuyên đề Toán lớp 4 đầy đủ lý thuyết và các dạng bài tập đa dạng có lời giải từ cơ bản đến nâng cao mới nhất năm 2023-2024 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 4.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(629 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 15 đề thi cuối kì 1 Toán lớp 4 Kết nối tri thức có đáp án150.000 ₫ 51.3 K 25.7 K lượt tải
-
Bộ 15 đề thi cuối kì 1 Toán lớp 4 Chân trời sáng tạo có đáp án150.000 ₫ 12.1 K 6.1 K lượt tải
-
Bộ 15 đề thi cuối kì 1 Toán lớp 4 Cánh diều có đáp án150.000 ₫ 20.9 K 10.5 K lượt tải
-
Đề cương ôn tập cuối học kì 1 Toán lớp 4 Kết nối tri thức80.000 ₫ 9.5 K 4.7 K lượt tải
-
Đề cương ôn tập cuối học kì 1 Toán lớp 4 Chân trời sáng tạo80.000 ₫ 4.8 K 2.4 K lượt tải
-
Bài tập cuối tuần Toán lớp 4 Kết nối tri thức (Cả năm180.000 ₫ 22.5 K 11.3 K lượt tải
-
Bộ 7 đề thi giữa kì 1 Toán lớp 4 Kết nối tri thức có đáp án110.000 ₫ 106.8 K 53.4 K lượt tải
-
Bộ 50 đề thi Toán lớp 4 cuối kì 1 năm 2022 - 2023150.000 ₫ 20.5 K 10.3 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 4
Xem thêm-
Bộ 10 đề thi cuối kì 1 Tiếng Việt lớp 4 Kết nối tri thức có đáp án150.000 ₫ 20.1 K 10 K lượt tải
-
Bộ 5 đề thi cuối kì 1 Tiếng Anh lớp 4 Family and Friends có đáp án90.000 ₫ 2.6 K 1.3 K lượt tải
-
Bộ 3 đề thi cuối kì 1 Lịch sử & Địa lí lớp 4 Kết nối tri thức có đáp án70.000 ₫ 7.9 K 4 K lượt tải
-
Bộ 10 đề thi cuối kì 1 Tiếng Việt lớp 4 Chân trời sáng tạo có đáp án150.000 ₫ 11.4 K 5.7 K lượt tải
-
Đề thi cuối kì 1 Khoa học lớp 4 Kết nối tri thức có đáp án50.000 ₫ 4.6 K 2.3 K lượt tải
-
Bài tập cuối tuần Tiếng việt lớp 4 Kết nối tri thức (Cả năm180.000 ₫ 9 K 4.5 K lượt tải
-
Bộ 5 đề thi cuối kì 1 Tiếng Anh lớp 4 i-Learn Smart Start có đáp án90.000 ₫ 1.8 K 0.9 K lượt tải
-
Đề thi cuối kì 1 Khoa học lớp 4 Chân trời sáng tạo có đáp án50.000 ₫ 3.6 K 1.8 K lượt tải
Tài liệu bộ mới nhất
CHUYÊN ĐỀ 18:
CÁC BÀI TOÁN LIÊN QUAN ĐẾN PHÂN SỐ
A- LÝ THUYẾT
I – Kiến thức cần nhớ
1. Phân số:
Với a là một số tự nhiên và b là một số tự nhiên khác 0, số có dạng
a
b
gọi là
phân số (đọc là: a phần b)
a gọi là: tử số (số phần lấy ra)
b gọi là: mẫu số (số phần bằng nhau được chia trong một đơn vị)
Ví dụ:
12 36 7 9
; ; ;
25 42 158 5
... là các phân số
Một số tự nhiên a chia cho số tự nhiên b (b
0) có kết quả chính là phân số
a
b
a : b =
a
b
Ví dụ: 5 : 12 =
5
12
Như vậy ta xem dấu “gạch ngang: của phân số như là dấu chia.
Ta có thể dùng phân số để ghi kết quả của phép chia một số tự nhiên cho một số
tự nhiên (Cho dù phép chia đó là phép chia hết hay phép chia có dư)
Một số tự nhiên có thể viết dưới dạng phân số có mẫu số là 1: a =
1
a
2. Một số tính chất cơ bản của phân số
Nếu ta nhân hay chia tử số và mẫu số của một phân số cùng với một số tự nhiên
khác 0 thì ta được một phân số mới bằng phân số đã cho
:
:
a a m a n
b b m b n
==
(với
0, 0mn
)
Ví dụ:
18 18 2 36 18:3 6
36 36 2 72 36:3 12
= = = =
3. Phân số tối giản
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho một số
tự nhiên nào khác 1.
Ví dụ:
1 15 27
; ; ;...
3 17 29
4. Rút gọn phân số
Muốn rút gọn phân số ta chia cả tử số và mẫu số của phân số đó với cùng một
số tự nhiên lớn hơn 1 mà tử số và mẫu số của phân số đó cùng chia hết cho số đó, để
được phân số mới có tử số và mẫu số nhỏ hơn tử số và mẫu số ban đầu và có giá trị
bằng phân số ban đầu.
Ví dụ:
15 15:15 1
60 60:15 4
==
Chú ý:
- Phân số tối giản không thể rút gọn được
- Khi rút gọn phân số cố gắng rút gọn đến phân số tối giản
- Dựa vào dấu hiệu chia hết hoặc phép thử chọn để tìm được một số tự nhiên nào
đó lớn hơn 1 mà cả tử số và mẫu số của phân số đã cho đều chia hết cho số đó.
- Các Bước Rút Gọn Phân Số:
+ B1: Tìm số tự nhiên lớn hơn 1 mà cả tử số và mẫu số của phân số đã cho đều chia
hết. (Dấu hiệu chia hết)
+ B2: Tiến hành chia cả tử số và mẫu số của phân số cho số tự nhiên đã tìm được ở
bước 1.
+ Lặp lại bước 1, 2 cho đến khi được phân số tối giản.
Ví Dụ : Rút gọn các phân số sau:
a)
9
18
b)
75
115
c)
1414
2727
d)
201620162016
201720172017
Hướng dẫn
a)
9 9:9 1
18 18:9 2
==
b)
75 75:5 15
115 115:5 23
==
c)
1414 1414:101 14
2727 2727:101 27
==
Các phân số dạng
...
ababab
cdcdcd
thì tử số và mẫu số sẽ chia hết cho các số: 101; 10101;
1001....Khi rút gọn được:
...
ab
cd
d)
201620162016 201620162016:100010001 2016
201720172017 201720172017:100010001 2017
==
5. Quy đồng phân số.
5.1. Quy Đồng Mẫu Số:
a) K/N: Quy đồng mẫu số là làm cho các phân số cần quy đồng có chung một mẫu số.
b) Phương pháp:
Phương pháp 1: Lấy tử số và mẫu số của phân số này nhân với mẫu số của phân số
kia.
Ví Dụ: Quy đồng mẫu số hai phân số sau:
3
4
và
4
7
Hướng dẫn
Ta có:
3 3 4 21
4 4 7 28
==
và
4 4 4 16
7 7 4 28
==
Vậy sau khi quy đồng mẫu số hai phân số
3
4
và
4
7
ta được hai phân số mới có cùng
mẫu số tương ứng là:
21
28
và
16
28
Phương pháp 2: Khi mà mẫu số của các phân số cùng chia hết cho một số tự nhiên lớn
hơn 1.
B1: Tìm số tự nhiên lớn hơn 1 mà các mẫu số cùng chia hết.
B2: Tính tích các mẫu số.
B3: Chia tích vừa tìm được ở bước 2 cho số tự nhiên tìm được ở bước 1. Thì kết quả
tìm được sẽ là mẫu số chung cần tìm.
B4: Chia mẫu số chung cho các mẫu số được một số. Tiến hành nhân cả tử số và mẫu
số của phân số đó cho số vừa tìm được.
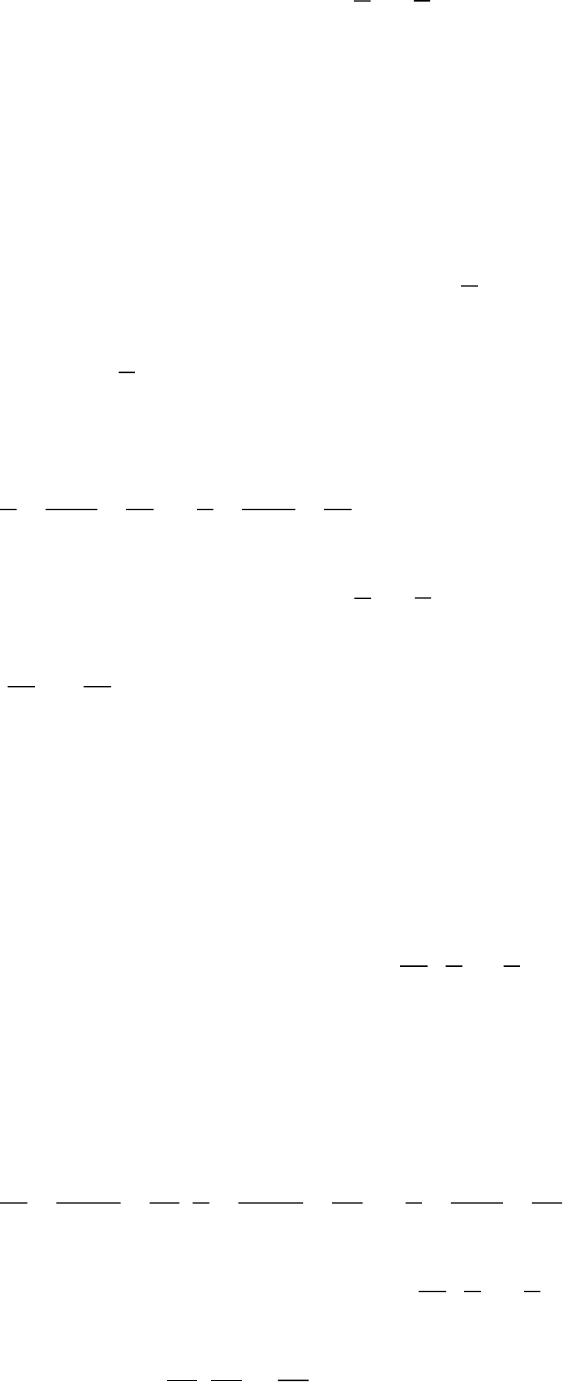
Ví dụ: Quy đồng mẫu số các phân số:
1
4
và
5
6
Hướng dẫn
B1: Cùng chia hết cho 2.
B2: Tích các mẫu số: 4 6 = 24
B3: Mẫu số chung là: 24 : 2 = 12
B4: Ta có: 12 : 4 = 3 cần nhân cả tử và mẫu của
1
4
với 3. Cũng có: 12 : 6 = 2 cần nhân
cả tử và mẫu của
5
6
với 2.
Bài giải:
Ta có:
1 1 3 3
4 4 3 12
==
và
5 5 2 10
6 6 2 12
==
Sau khi quy đồng mẫu số hai phân số
1
4
và
5
6
ta được hai phân số cùng mẫu số tương
ứng là:
3
12
và
10
12
Phương pháp 3: Khi mà mẫu số của các phân số cùng chia hết cho một số tự nhiên lớn
hơn 1. Ta chọn ra mẫu số lớn nhất, nhân mẫu số đó lần lượt với 2, 3, 4... cho đến khi
được một số mà chia hết cho tất cả các mẫu số của các phân số còn lại thì số đó ta lấy
làm mẫu số chung.
Ví dụ: Quy đồng mẫu số các phân số sau:
72
;
15 3
và
5
6
Phân tích: 15 là mẫu số lớn nhất. 15 chia hết cho 3. Thấy: 15 2 = 30 chia hết cho 6.
Suy ra: mẫu số chung là 30.
Hướng dẫn
Ta có:
7 7 2 14 2 2 10 20
;
15 15 2 30 3 3 10 30
= = = =
và
5 5 5 25
6 6 5 30
==
Vậy sau khi quy đồng mẫu số các phân số
72
;
15 3
và
5
6
ta được các phân số có cùng
mẫu số tương ứng là:
14 20
;
30 30
và
25
30
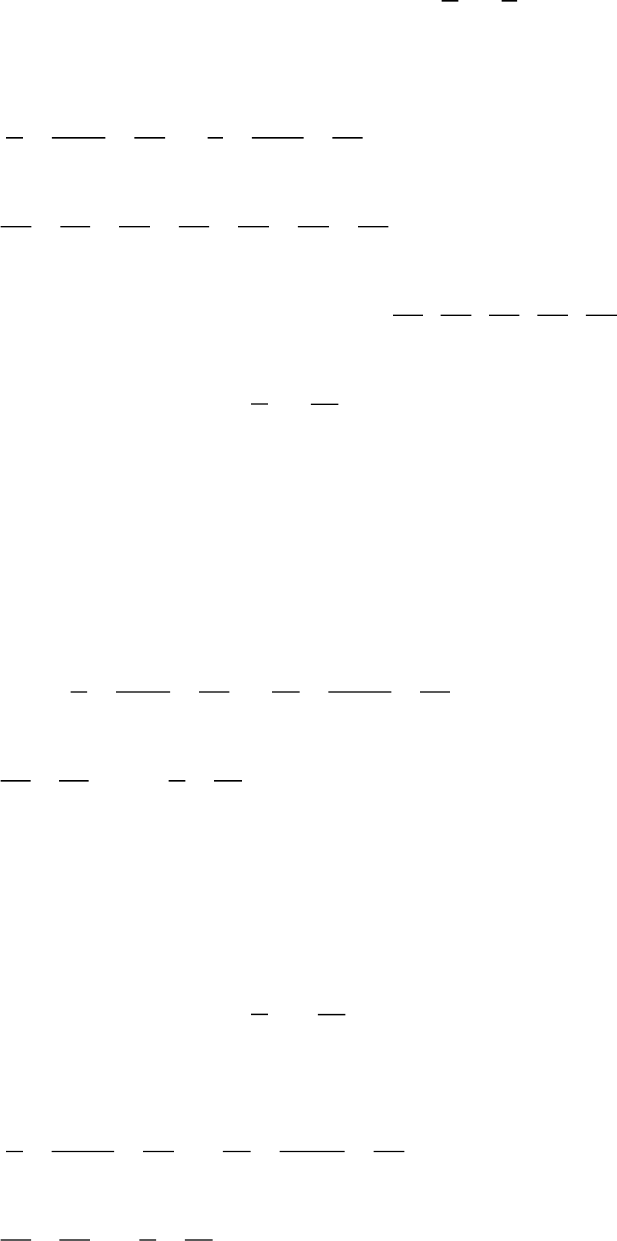
Ví dụ: Viết 5 phân số đứng giữa hai phân số:
5
7
và
5
8
Hướng dẫn
Ta có:
5 5 6 30
7 7 6 42
==
và
5 5 6 30
8 8 6 48
==
Thấy:
30 30 30 30 30 30 30
42 43 44 45 46 47 48
Chọn được 5 phân số thỏa mãn đề bài là:
30 30 30 30 30
; ; ; ;
43 44 45 46 47
Ví Dụ: So sánh hai phân số:
7
9
và
11
12
Hướng dẫn
Phân tích: 9 và 12 đều chia hết cho 3. Lấy 12
2 = 24 không chia hết cho 9.
Lấy 12
3 = 36 chia hết cho 9
Mẫu số chung là 36.
Bài giải
Ta có
7 7 4 28
9 9 4 36
==
và
11 11 3 33
12 12 3 36
==
Thấy:
28 33
36 36
do đó
7 11
9 12
5.2. Quy Đồng Tử Số:
- Quy đồng tử số: Làm cho tử số của các phân số cần quy đồng bằng nhau.
- Phương pháp: Tương tự như quy đồng mẫu số
Ví Dụ: So sánh hai phân số:
7
9
và
11
12
bằng cách quy đồng tử số.
Hướng dẫn
Ta có:
7 7 11 77
9 9 11 99
==
và
11 11 7 77
12 12 7 84
==
Thấy:
77 77
99 84
nên
7 11
9 12
6. Cách đọc phân số
Nếu tử số và mẫu số của phân số là các số thì đọc là phần, còn có chữ số thì đọc
là trên
Ví dụ:
3
2
đọc là ba phần hai;
a
b
đọc là a trên b;
2
a
đọc là a trên 2
BÀI TẬP TỰ LUYỆN
1. “Năm phần mười sáu” là cách đọc của phân số hoặc phép tính:
16 6 5
; ; 5:16;
5 5 16
2. Cho các phân số:
9 15 15 18 24 17
; ; ; ; ;
12 16 20 25 36 25
. Tìm phân số bằng phân số
3
4
?
3. Phân số
2
5
được đọc là ....
4. Các phân số nhỏ hơn 1 có mẫu số là 5 và có tử số khác 0 là: ...
5. Phân số nào bằng phân số
3 9 12 6 9
? ; ; ;
8 24 18 12 16
6. Tìm phân số có mẫu số là 25 và bằng phân số
24 24 36 75
. ; ; ;
10 25 25 25
60
25
7. Cho các phân số:
3 4 5 6 4 12
; ; ; ; ;
60 12 6 9 3 60
. Trong các phân số đã cho các phân số tối
giản là: …..
8. Viết số 5 dưới dạng phân số có mẫu là 3 được kết quả là: …..
9. Rút gọn phân số
56
72
được phân số tối giản là:...
10. Quy đồng mẫu số hai phân số
5
6
và
3
8
, với mẫu số chung là 24 ta được : .
11. Viết phân số: Bốn mươi ba phần sáu mươi lăm được viết là:..
12. Tìm a biết:
12
30 85
a
=
13. Tìm a biết:
24
36 54
a
=
14. Tìm a biết:
21 15
20a
=
15. Điền số thích hợp vào chỗ chấm:
48 ...
208 13
=
16. Rút gọn phân số
504
567
đến phân số tối giản ta được phân số
a
b
. Khi đó a b = …
17. Rút gọn phân số
116
56
đến phân số tối giản ta được phân số
m
n
. Khi đó m – n = …
18. Cho hai phân số bằng nhau:
13 585
4 a
=
. Tính a.
19. Rút gọn phân số
72
84
ta được phân số tối giản là: ...
20. Cho các phân số:
7 8 12 25
; ; ;
35 20 60 50
. Trong các phân số đó phân số nào bằng phân số
20
100
21. Mẫu số chung nhỏ nhất của các phân số:
5 7 9 11
; ; ;
4 8 10 20
là ……
22. Để rút gọn phân số
207207
324324
thành phân số tối giản, ta phải chia cả tử số và mẫu số
cho bao nhiêu?
23. Khi quy đồng mẫu số ba phân số
84
;
45 15
và
7
30
, mẫu số chung nhỏ nhất của ba
phân số là ...
24. Rút gọn
75
100
được phân số tối giản là...
25. Tìm giá trị của a để:
1
5
a
=
26. Mẫu số của phân số
3
4
là: …..
27. Tìm a để: 85 : 96 =
96
a
28. Tử số của phân số
15
13
29. Quy đồng mẫu số của hai phân số
3
4
và
5
8
được hai phân số có mẫu số chung
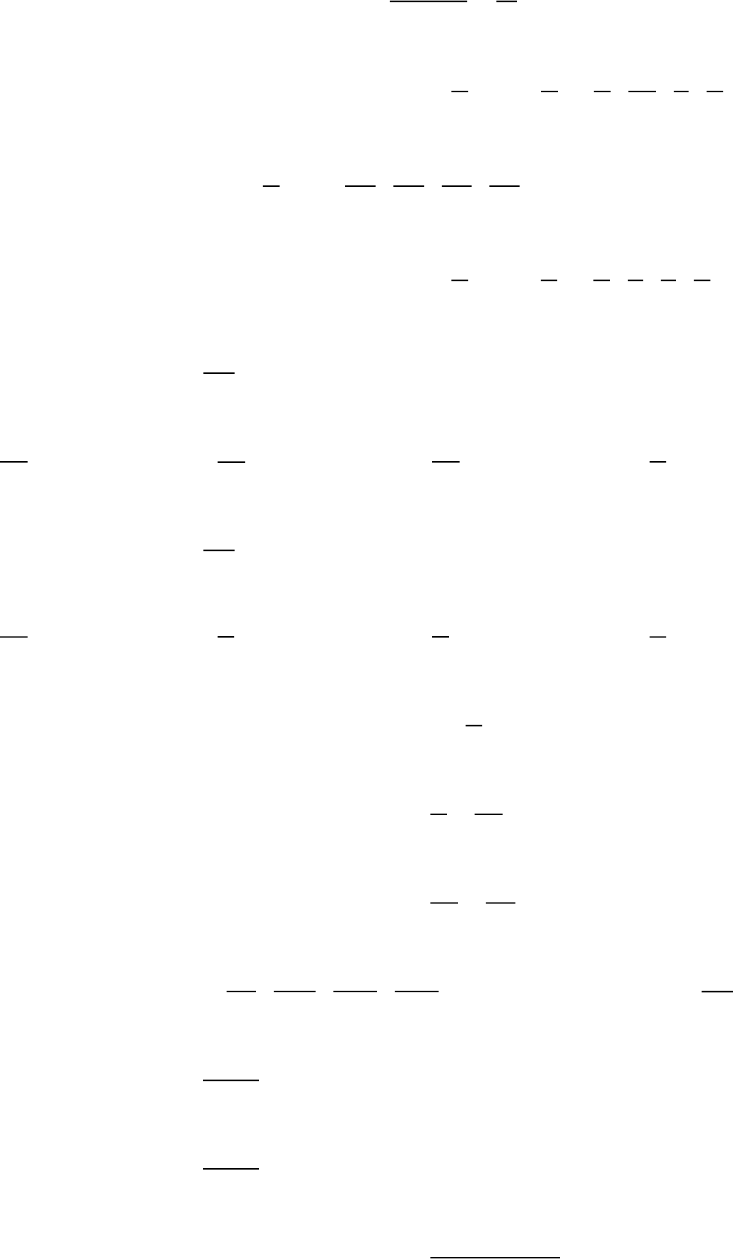
nhỏ nhất là: ...
30. Điền số thích hợp vào chỗ chấm:
16 9 9
32 13 ...
=
31. Điền phân số thích hợp vào chỗ chấm:
1 2 1 5 1 2
... ; ; ;
4 3 2 12 3 5
+=
32. Phân số bằng phân số
2
3
là:
18 30 16 38
; ; ;
24 20 30 57
33. Điền phân số thích hợp vào chỗ chấm:
1 1 1 1 1 2
... ; ; ;
2 6 4 5 3 3
−=
34. Rút gọn phân số
8
20
được phân số tối giản là:
a)
4
10
b)
1
12
c)
4
16
d)
2
5
35. Rút gọn phân số
16
24
được phân số tối giản là:
a)
8
12
; b)
4
6
; c)
2
3
; d)
1
2
36. Điền phân số tối giản vào chỗ chấm:
4
1 ...
7
+=
37. Điền phân số tối giản vào chỗ chấm:
9 17
...
46
+=
38. Điền phân số tối giản vào chỗ chấm:
9 13
...
14 35
+=
39. Trong các phân số
80 150 338 390
; ; ;
15 25 65 45
phân số bằng phân số
26
5
là: …..
40. Rút gọn phân số
1960
1008
ta được phân số tối giản là: …
41. Rút gọn phân số
1200
1728
ta được phân số tối giản là: …
42. Điền phân số tối giản vào chỗ chấm:
12 25 42
10 24 36
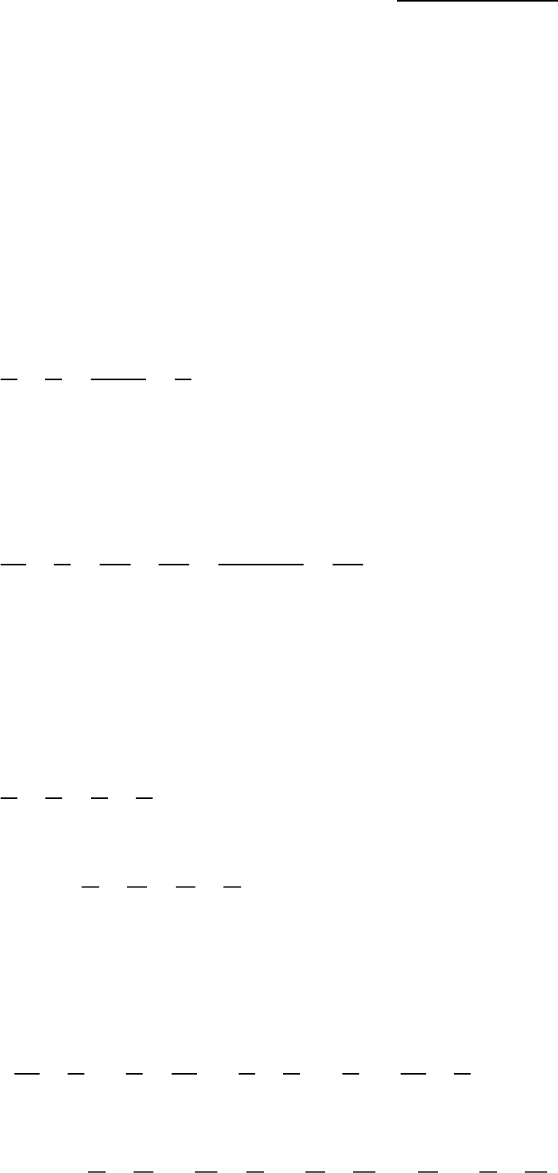
43. Điền phân số tối giản vào chỗ chấm:
6 8 10 12
9 10 11 24
II − Các dạng toán
DẠNG 1. BỐN PHÉP TÍNH VỀ PHÂN SỐ
1. Phép Cộng Phân Số:
1.1. Phép cộng phân số:
- Muốn cộng hai phân số cùng mẫu số ta cộng tử số của phân số thứ nhất với tử số của
phân số thứ hai và giữ nguyên mẫu số.
VD:
3 2 3 2 5
7 7 7 7
+
+ = =
- Muốn cộng hai phân số khác mẫu số: ta quy đồng mẫu số hai phân số đó, rồi tiến hành
cộng hai phân số.
VD:
3 2 27 22 27 22 49
11 9 99 99 99 99
+
+ = + = =
1.2. Tính chất:
a) Tính chất giao hoán: Khi đổi chỗ các phân số trong tổng thì giá trị của tổng không
đổi.
VD:
1 3 3 1
7 4 4 7
+ = +
Tổng quát:
a c c a
b d d b
+ = +
(b, d > 0)
b) Tính chất kết hợp: Khi cộng một tổng với phân số thứ ba, ta có thể cộng phân số thứ
nhất với tổng của phân số thứ hai và phân số thứ ba.
VD:
3 4 2 3 4 2 4 3 2
11 9 7 11 9 7 9 11 7
+ + = + + = + +
Tổng quát:
a c e a c e c a e
b d f b d f d b f
+ + = + + = + +
(b, d, f > 0)
2. Phép Trừ Phân Số:
- Muốn trừ phân số cùng mẫu số ta trừ tử số của phân số thứ nhất cho tử số của phân
số thứ hai và giữ nguyên mẫu số.
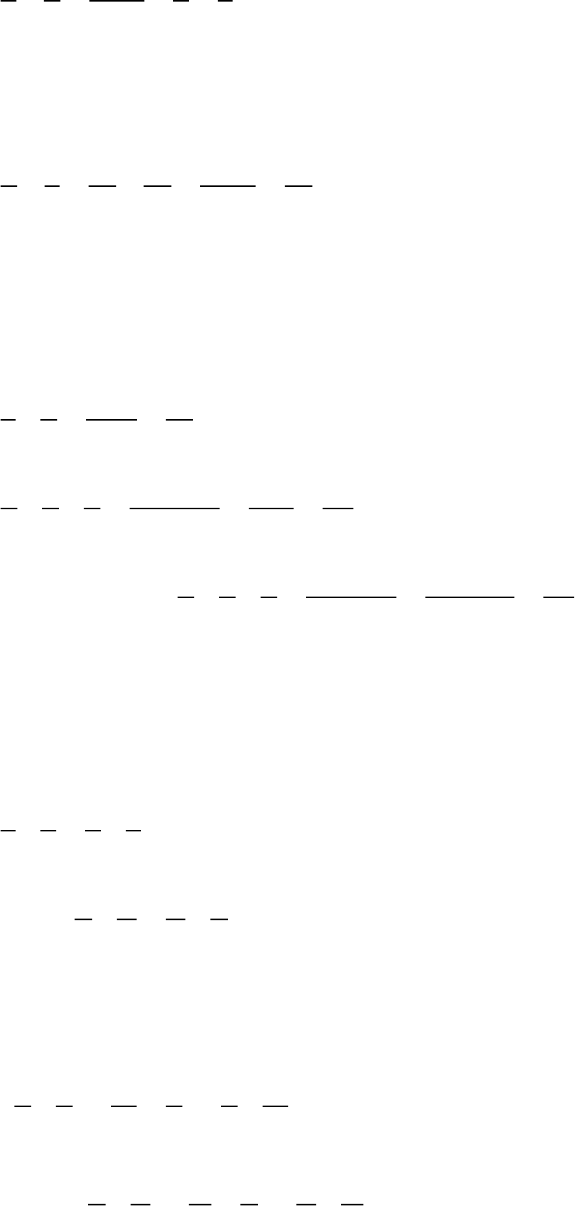
VD:
5 2 5 2 3 1
9 9 9 9 3
−
− = = =
- Muốn trừ hai phân số khác mẫu số: ta quy đồng mẫu số của hai phân số đó, rồi trừ
hai phân số.
VD:
3 1 9 4 9 4 5
4 3 12 12 12 12
−
− = − = =
3. Phép Nhân Phân Số:
3.1. Phép nhân hai phân số: Nhân tử số của phân số thứ nhất với tử số của phân số
thứ hai và mẫu số của phân số thứ nhất với mẫu số của phân số thứ hai.
VD:
1 2 1 2 2
3 5 3 5 15
= =
VD:
3 2 1 3 2 1 6 1
4 9 7 4 9 7 252 42
= = =
Có thể làm như sau:
3 2 1 3 2 1 1 1 1 1
4 9 7 4 9 7 2 3 7 42
= = =
3.2. Tính chất:
a) Tính chất giao hoán: Khi đổi chỗ các phân số trong một tích thì giá trị của tích đó
không đổi.
VD:
1 5 5 1
3 9 9 3
=
Tổng quát:
a c c a
b d d b
=
(b , d > 0)
b) Tính chất kết hợp: Khi nhân một tích với một phân số thứ ba, ta có thể nhân phân
số thứ nhất với tích của phân số thứ hai và thứ ba.
VD:
3 1 7 3 1 7
4 2 11 4 2 11
=
Tổng quát:
a c e a c e
b d f b d f
=
(b, d, f > 0)
c) Tính chất phân phối: Khi nhân một tổng của hai phân số với phân số thứ ba ta có
thể làm như sau: nhân phân số thứ nhất với phân số thứ ba và nhân phân số thứ hai với
phân số thứ ba rồi tính tổng các kết quả thu được.
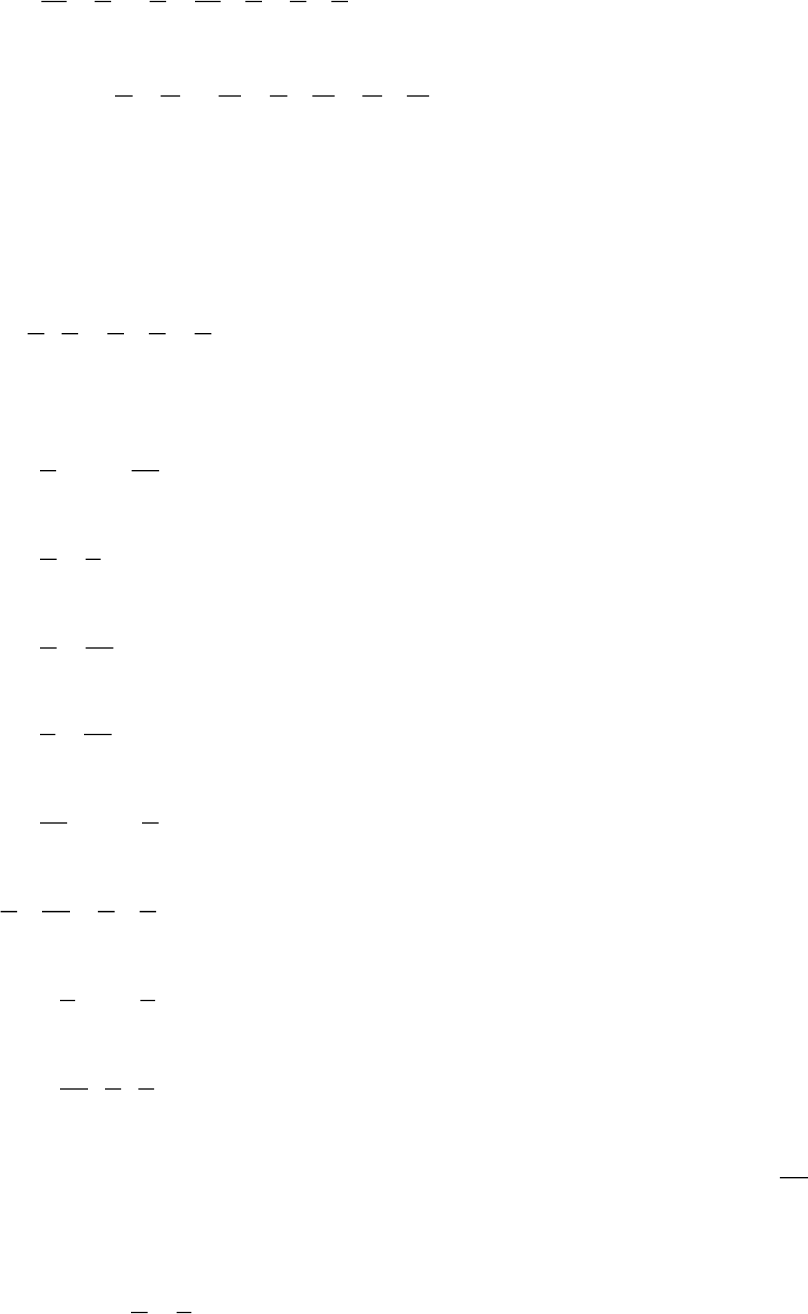
VD:
3 4 1 3 1 4 1
11 7 2 11 2 7 2
+ = +
Tổng quát:
a c e a e c e
b d f b f d f
+ = +
(b, d, f > 0)
4. Phép Chia Phân Số:
- Muốn chia hai phân số ta làm như sau: Lấy phân số thứ nhất nhân với phân số đảo
ngược của phân số thứ hai.
VD:
1 3 1 7 7
:
2 7 2 3 6
= =
BÀI TẬP TỰ LUYỆN
1. Để
6 16
55
m+=
thì m là …..
2. Để
28
33
m=−
thì m là …..
3. Để
1 17
44
m=−
thì m là …..
4. Để
1 16
55
m=−
thì m là …..
5. Để
15 8
77
m−=
thì m là …..
6.
3 14 3 7
....
7 3 7 3
+ =
7. Tính
18
16: ...
33
=
8. Tính
10 1 5
: : ...
3 6 9
=
9. Khi nhân cả tử số và mẫu số của một phân số với 3, ta được phân số
6
21
. Hỏi phân
số đó là bao nhiêu?
10.Tìm m để:
28
33
m=−
11.Tìm m để:
1 17
44
m=−
12.Tìm m để:
6 16
55
m+=
13.Trong các biểu thức sau, biểu thức nào có giá trị bằng
8
5
?
A.
3
1
5
+
B.
1
8
5
+
C.
11111
88888
++++
D.
3
1
5
−
14.Tính giá trị của biểu thức:
111
234
++
15.Hiệu của
3
5
và
1
5
là
16.Bớt
1
4
từ 1 sẽ được: ...
17.Tìm phân số thích hợp điền vào chỗ chấm :
4
... 1
5
+=
18.Tính giá trị biểu thức:
1 1 1 1
1
3 6 12 24
− − − −
19.
2
3
của 18 là: …
20. Nếu
2
3
của X là 12 thì X là: …
21.
18
16:
33
22. Tính:
10 1 5
::
3 6 9
23. Tìm a biết:
23
9 8 4
a
=
24. Tính: 5 : 15 : 20 = …
25. Tính:
1 1 1
4 6 8
++
26. Tính:
75
12 12
+
27. Tính:
72
15 10
+
28. Tính:
84
33
+
29. Tính:
31
45
+
30. Tính:
5 3 4
12 9 36
++
31. Tính:
58 63
42 87
32. Tính:
38 27 3
81 57
33. Tính:
17 23 28 1 26 22
45 45 45 27 27 45
+ + + + +
34. Tính:
24 7 31 5
29 38 38 29
+++
35. Tính:
3 5 7
21 10
36. Tính:
1002 72 108
9018 162 243
++
37. Tính:
7 3 14 125 25
21 21 21 175 175
+ + + +
38. Tính:
14 5 1
15 6 2
−+
39.
7
5
của 150 là: …
40. Tổng của
5
6
và
13
6
là …
41. Hiệu của
11
4
và
3
4
là: …
42. Để
71
22
m−=
thì m là …
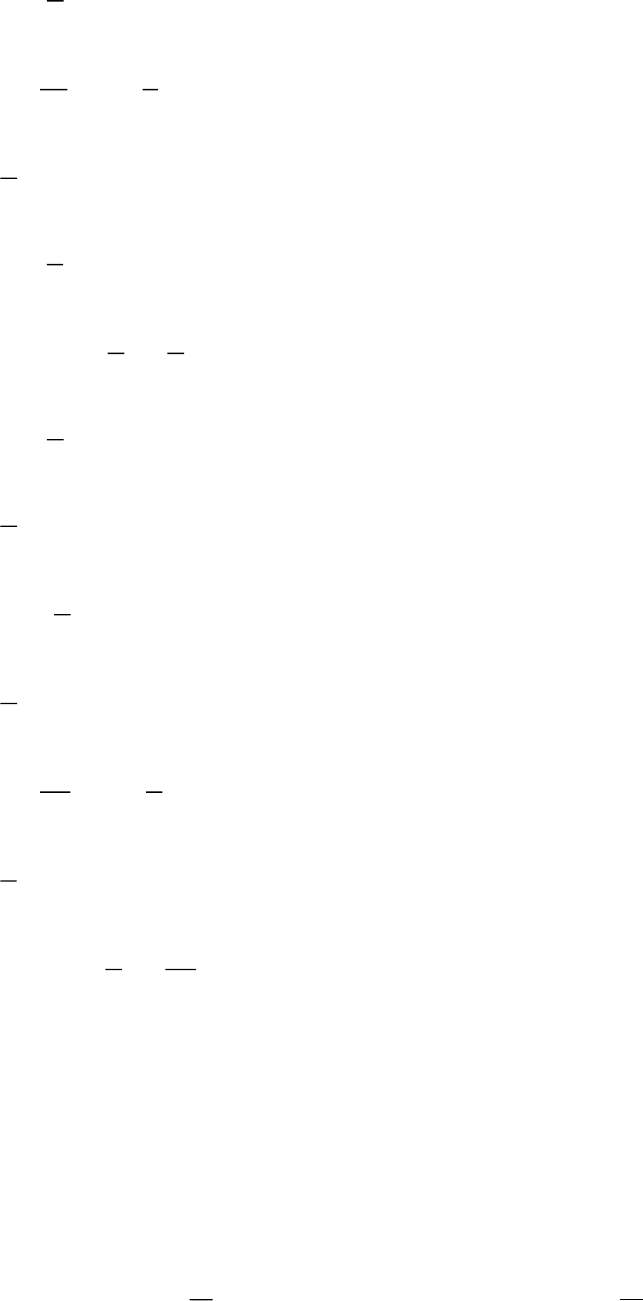
43.Nếu
7
6
của t là 147 thì t là ...
44. Để
19 1
99
m−=
thì m là …
45.
7
4
của 100 là …
46.Nếu
6
5
của y là 66 thì y là …
47. Hiệu của
3
2
và
1
2
là …
48.Nếu
7
4
của m là 175 thì m là …
49.
7
6
của 126 là …
50. Nếu
7
8
của k là 2009 thì k là ...
51.
7
8
của 2296 là …
52. Để
25 1
66
m−=
thì m là …
53.
6
5
của 55 là ...
54.Tổng của
3
7
và
25
7
là …
DẠNG 2: TÌM PHÂN SỐ CỦA MỘT SỐ
GHI NHỚ:
- Muốn tìm giá trị phân số của một số cho trước, ta nhân số cho trước với phân số đó.
Tổng quát:
Muốn tìm số a bằng
m
n
của số b cho trước, ta tính: a = b
m
n
(
, , 0m n N n
)
- Tìm một số khi biết phân số và giá trị của phân số ta lấy giá trị phân số chia cho phân
số.
Ví dụ 1: Mẹ 49 tuổi ,tuổi con bằng
2
7
tuổi mẹ .Hỏi con bao nhiêu tuổi?
Bài giải
Tuổi con là:
2
49 14
7
=
tuổi.
Đáp số : 14 tuổi.
Ví dụ 2: Bác An có một thửa ruộng. Trên thửa ruộng ấy bác dành
1
2
diện tích để trồng
rau,
1
3
để đào ao phần còn lại dành làm đường đi. Biết diện tích làm đường đi là 30m
2
. Tính diện tích thửa ruộng.
Bài giải
Số phần còn lại để bác An làm diện tích đường đi là:
1 1 1
1
2 3 6
− − =
(diện tích)
Diện tích thửa ruộng là
1
30: 180
6
=
(m
2
)
Đáp số: 180m
2
BÀI TẬP TỰ LUYỆN
1. Có hai thùng dầu, thùng thứ nhất sau khi lấy ra 12l thì số dầu còn lại bằng
1
3
thùng
thứ hai. Thùng thứ hai lấy ra 5l thì còn lại trong thùng 49l. Tính số dầu có ở cả hai
thùng
2. Mẹ có 3kg đường, mẹ dùng
1
4
số đường để làm bánh, mẹ dùng
1
5
số đường còn lại
để pha nước uống. Hỏi mẹ còn lại bao nhiêu gam đường?
3. Một cửa hàng có 6 tấm vải, mỗi tấm vải dài 35m. Cửa hàng đã bán
1
3
số vải. Vậy
cửa hàng đã bán ....m
4. Lớp 4A có 32 học sinh, trong đó
1
4
số học sinh là học sinh giỏi. Số học sinh khá
chiếm
1
2
số học sinh cả lớp, còn lại là học sinh trung bình không có học sinh yếu kém.
Phân số chỉ phần học sinh trung bình trong số học sinh của lớp 4A là: ...
5. Khối 4 một trường Tiểu học có 72 học sinh,trong đó có
1
4
số học sinh được xếp loại
trung bình, số học sinh còn lại xếp loại khá và giỏi. Tính số học sinh xếp loại khá và
giỏi của khối 4 đó.
6. Tuổi của anh bằng
2
5
tuổi cha, tuổi của em bằng
1
2
tuổi anh. Tính tuổi em biết rằng
hiện nay cha 45 tuổi.
7. Một cửa hàng nhập về 44 can nước mắm, mỗi can chứa 5l. Cửa hàng đã bán
1
4
số
nước mắm đó. Cửa hàng còn lại ........l nước mắm.
8. Một cửa hàng nhập về 6 bao gạo, mỗi bao chứa 150kg gạo. Cửa hàng đã bán
1
4
số
gạo đó. Cửa hàng đã bán …….kg gạo.
9. Một người phải đi một quãng đường dài 280 km trong 3 ngày. Ngày thứ nhất người
đó đi được
1
4
quãng đường, ngày thứ hai người đó đi được
2
5
quãng đường còn lại. Hỏi
ngày thứ ba người đó phải đi bao nhiêu ki-lô-mét nữa.
10.An có một túi bi gồm 135 viên. An chia cho Bình
2
5
số bi của mình. Sau đó An cho
Chi
1
3
số bi còn lại. Hỏi Bình có nhiều hơn Chi bao nhiêu viên bi?
11.Một kho chứa 126 hộp mứt tết, biết trong đó có
7
9
số mứt được chuyển tặng các em
bé vùng cao ăn tết. Số còn lại chia đều làm quà tết cho 14 gia đình neo đơn. Mỗi gia
đình neo đơn nhận......hộp mứt tết.
12.Bạn Minh đếm trong nhà xe của trường có tất cả 216 xe máy và xe đạp, số xe đạp
chiếm
4
9
tổng số xe. Trong nhà xe có tất cả ……….xe máy.
13.Một thửa ruộng có diện tích là 360m
2
, người ta dành
3
4
diện tích để cấy lúa, phần
còn lại để trồng khoai. Biết rằng cứ 3m
2
người ta thu được 7kg khoai. Số khoai thu
được là : ...... kg.
14.Điểm thi môn Tiếng Việt hết kì I của lớp 4B có
1
5
số bạn đạt điểm giỏi,
1
6
số bạn
đạt điểm trung bình. Số bạn còn lại đều đạt điểm khá. Biết lớp 4B có 30 bạn. Số bạn
đạt điểm khá là : ……
15.Điểm thi môn Toán hết kì I của lớp 4A có
1
4
số bạn đạt điểm giỏi,
1
8
số bạn đạt điểm
trung bình. Số bạn còn lại đều đạt điểm khá. Biết lớp 4A có 32 bạn. Số bạn đạt điểm
khá là : ……..
16.Mảnh ruộng hình chữ nhật có chiều rộng 20m, chiều dài bằng
7
5
chiều rộng. Diện
tích mảnh ruộng là...m
2
17.Hình chữ nhật có chu vi 1m, chiều dài
3
10
m thì chiều rộng là ...dm
18.Hình chữ nhật có chu vi
7
5
m, chiều dài 4dm. Diện tích hình chữ nhật là...dm
2
.
19. Một thùng đựng 54 cái bánh, mỗi cái bánh nặng
2
9
kg. Hỏi thùng bánh đó nặng bao
nhiêu ki-lô-gam?
20.Một cửa hàng có 60 xe máy. Buổi sáng bán được
3
20
số xe máy đó, buổi chiều bán
được
4
17
số xe máy còn lại. Hỏi sau hai buổi bán cửa hàng còn lại bao nhiêu xe máy?
21. Người ta cho một vòi chảy vào một vể hết nước lần thứ nhất vòi chảy được một
nửa bể. Lân thứ hai vòi chảy được
2
5
bể. Em hãy tính xem bể có thể chứa được bao
nhiêu lít nước biết rằng nếu vòi chảy thêm được 1000 lít nữa thì vừa đầy bể?
22.Giá tiền một quyển sách là 4000 đồng. Nếu giảm
1
5
giá bán thì mua quyển sách đó
phải trả bao nhiêu tiền?
23.Số tự nhiên có ba chữ số mà chữ số hàng trăm bằng
1
3
chữ số hàng đơn vị và chữ số
hàng chục bằng
1
2
chữ số hàng đơn vị là: ……
24.Mẹ 36 tuổi,tuổi con bằng
1
6
tuổi mẹ hỏi bao nhiêu năm nữa tuổi con bằng
1
3
tuổi
mẹ?
25.Trong đợt kiểm tra học kì vừa qua ở khối 4 thầy giáo nhận thấy
1
2
số học sinh đạt
điểm giỏi,
1
3
số học sinh đạt điểm khá,
1
10
số học sinh đạt trung bình còn lại là số học
sinh đạt điểm yếu .Tính số học sinh đạt điểm yếu biết số học sinh giỏi là 45 em.
26.Một cửa hàng nhận về một số hộp xà phòng. Người bán hàng để lại
1
10
số hộp bày
ở quầy, còn lại đem cất vào tủ quầy .Sau khi bán 4 hộp ở quầy người đó nhận thấy số
hộp xà phòng cất đi gấp 15 lần số hộp xà phòng còn lại ở quầy. Tính số hộp xà phòng
cửa hàng đã nhập.
27. Một cửa hàng nhận về một số xe đạp. Người bán hàng để lại
1
6
số xe đạp bày bán,
còn lại đem cất vào kho. Sau khi bán 5 xe đạp ở quầy người đó nhận thấy số xe đạp cất
đi gấp 10 lần số xe đạp còn lại ở quầy. Tính số xe đạp cửa hàng đã nhập.
28.Một giá sách có 2 ngăn. Số sách ở ngăn dưới gấp 3 lần số sách ở ngăn trên. Nếu
chuyển 2 quyển từ ngăn trên xuống ngăn dưới thì số sách ở ngăn dưới sẽ gấp 4 lấn số
sách ở ngăn trên .Tính số sách ở mỗi ngăn.
29.Một ô tô giờ đầu chạy được
3
16
quãng đường, giờ thứ 2 chạy được
7
20
quãng đường.
Vậy sau 2 giờ xe máy đó chạy được bao nhiêu phần quãng đường?
30.Một túi kẹo có một số chiếc kẹo. Bạn Bình lấy
4
13
số kẹo trong túi, bạn Minh lấy
5
13
số kẹo trong túi. Hỏi cả hai bạn đã lấy mấy phần kẹo trong túi?
31.Một hình chữ nhật có chiều dài
7
8
m và chiều rộng
5
21
m. Tính nửa chu vi hình chữ
nhật đó. (Phân số tối giản)
32.Trong hội khỏe Phù Đổng có
1
8
số học sinh thi chạy;
1
9
số học sinh thi cầu lông còn
lại tất cả 110 em tham gia thi các môn khác. Hỏi trong hội thi có tất cả bao nhiêu em
tham gia? Biết mỗi em chỉ tham gia 1 môn thi?
33.Trường Thắng Lợi có một mảnh vườn diện tích 315m
2
trong đó
1
5
diện tích trồng
cây ăn quả, diện tích để ươm giống cây gấp đôi diện tích trồng cây ăn quả. Diện tích
trồng hoa bằng
1
3
diện tích ươm giống. Như vậy diện tích trồng hoa bao nhiêu?
34.Một người bán hoa quả lần thứ nhất bán
3
5
số quả xoài, lần thứ hai bán số xoài bằng
3
5
số xoài bán lần thứ nhất. Vậy số xoài còn lại là ... tổng số xoài.
35.Biết
2
3
khối lượng sữa trong một hộp sữa là
3
10
kg. Hỏi hộp sữa đó chứa bao nhiều
gam sữa?
36.Giá của một quyển sách là 20000 đồng. Nếu giảm
3
10
giá bán thì người mua quyển
sách đó chỉ phải trả bao nhiêu tiền?
37.Có 5 thùng dầu, mỗi thùng chứa 30l. Người ta đem đóng chai, mỗi chai
3
5
l
dầu.
Hỏi đóng được tất cả bao nhiêu chai dầu
38.Xe thứ nhất chở
1
2
tấn hàng, xe thứ hai chở
3
4
tấn hàng, xe thứ ba chở
2
5
tấn hàng.
Hỏi trung bình mỗi xe chở bao nhiêu ki-lô-gam hàng?
39.Cửa hàng bác Lan có 20 bao gạo, mỗi bao nặng 50kg. Bác đã bán
2
5
số gạo đó. Hỏi
cửa hàng của bác Lan còn lại bao nhiêu tạ gạo?
40.Một cửa hàng lần thứ nhất bán được
1
3
số thóc trong kho, lần thứ hai bán được
1
3
số thóc còn lại sau khi bán lần đầu, lần thứ ba bán được
1
3
số thóc còn lại sau khi bán
lần thứ hai. Sau ba lần bán, trong kho còn lại 600kg thóc. Hỏi lúc đầu trong kho có bao
nhiêu ki-lô-gam thóc?
41.Nhà Mai có một đàn gà, số gà mái bằng
3
4
số gà của cả đàn. Nếu mẹ nhốt 5 con gà
trống thì số gà mái bằng
6
7
số gà còn lại của cả đàn. Lúc đầu có ...con gà trống.
42.Có 1 số cam và quýt. Số quýt hơn số cam 20quả. Đã bán 40 quả quýt nên số quýt
còn lại bằng
3
5
số cam. Lúc đầu có ……….quả cam.
43.Nhà An nuôi 24 con gà; trong đó có
3
8
là gà trống. Gà mái hơn gà trống : …….
44.Khối 4 một trường Tiểu học có 96 học sinh, trong đó có
1
3
số học sinh được xếp
loại loại giỏi, số học sinh còn lại xếp loại khá và trung bình. Tính số học sinh xếp loại
khá và trung bình của khối đó.
45.Có 42 chiếc xe máy. Số xe máy bằng
1
7
số xe đạp. Hỏi số xe đạp nhiều hơn xe máy
bao nhiêu xe?
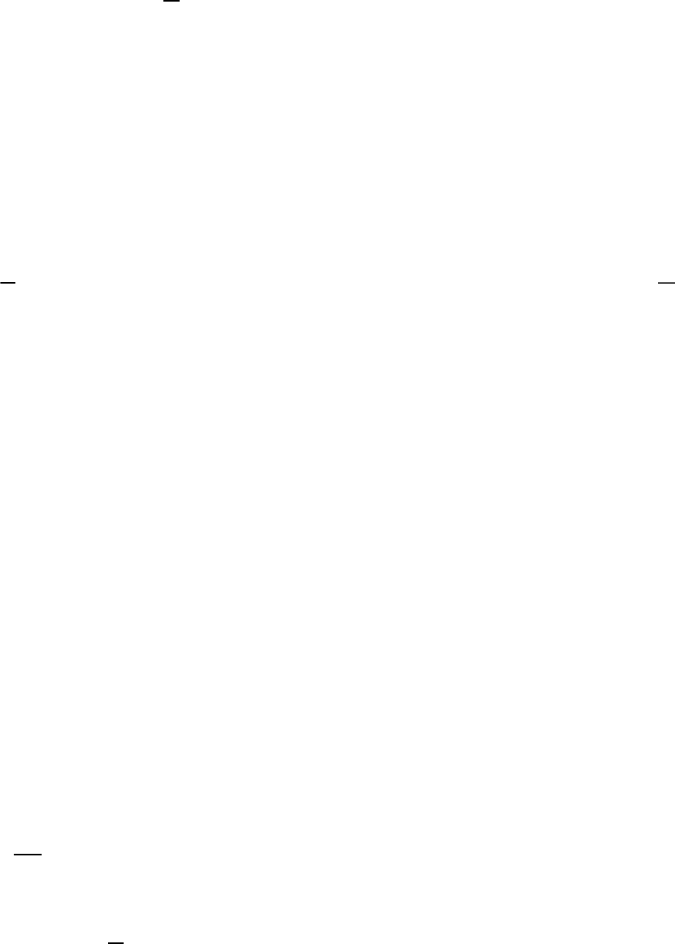
46.Có 36 xe đạp. Số xe máy bằng
1
6
số xe đạp. Hỏi số xe đạp nhiều hơn xe máy là bao
nhiêu xe?
47.Lớp 4A có 30 học sinh, trong đó có 16 học sinh nam. Tỉ số giữa học sinh nam và
học sinh nữ là : …….
48.Một đội công nhân dự định làm trong 3 ngày hết quãng đường dài 171m. Ngày thứ
nhất đội làm được
1
3
đoạn đường, ngày thứ hai làm được đoạn đường bằng
1
2
ngày
thứ nhất. Để hoàn thành công việc, ngày thứ ba đội cần làm .....m đường nữa.
DẠNG 3: CÁC DẠNG KHÁC
* Lưu ý:
- Khi thêm ở tử số hoặc MS và bớt ở MS hoặc tử số thì hiệu không thay đổi.
- Khi thêm vào tử số a đơn vị và bớt đi a đơn vị ở mẫu số của một phân số (hoặc ngược
lại) thì tổng của tử số và mẫu số không thay đổi
Dạng 3.1: Chuyển từ tử xuống mẫu, hoặc thêm vào tử bớt mẫu cùng một số hoặc
ngược lại.
Bài 1. Cho phân số
51
61
. Hỏi phải chuyển ở tử số xuống mẫu số bao nhiêu đơn vị để
được phân số có giá trị bằng
3
5
?
Hướng dẫn
Khi bớt tử số và thêm MS cùng một số đơn vị thì tổng không thay đổi. Nên tổng
của TS và MS của phân số mới bằng: 51 + 61 = 112
Tử số của phân số mới là: 112 : (3 + 5)
3 = 42
Số đơn vị phải chuyển: 51 – 42 = 9
Dạng 3.2: Cùng thêm (bớt) vào tử và mẫu
Bài 2. Cho phân số
56
81
. Hỏi cùng thêm vào tử số và mẫu số bao nhiêu đơn vị để được
phân số có giá trị bằng
3
4
?
Hướng dẫn
Hiệu của ts và ms là: 81 – 56 = 25
Từ số của phân số sau khi thêm: 25 : (4 – 3)
3 = 75
Số đơn vị phải thêm: 75 – 56 = 19
Dạng 3.3: Hiệu là ẩn phải xác định và thêm bớt để tìm hiệu mới
Bài 3. Tìm một phân số biết nếu chuyển 5 đơn vị từ mẫu số lên tử số thì được phân số
có giá trị bằng 1. Nếu chuyển 1 đơn vị từ tử số xuống mẫu số thì được phân số có giá
trị bằng
1
2
?
Hướng dẫn
Chuyển 5 đơn vị từ mẫu lên tử thì được phân số có giá trị bằng 1 nên hiệu sẽ là:
5
2 = 10
Chuyển 1 đơn vị ở tử mẫu nhận thêm 1 đơn vị hiệu mới là: 10 + 1 + 1 = 12
Tử số mới là: 12 : (2 – 1)
1 = 12;
Mẫu số mới là: 12 : (2 – 1)
2 = 24
Chuyển 1 đơn vị =12 thì tử số cũ là: 12 + 1 = 13
Mẫu nhận 1 đơn vị = 24 thì mẫu số cũ là: 24 – 1 = 23
Dạng 3.4: Thêm bớt ở tử hoặc ở mẫu
* Lưu ý:
- Quy đồng hai phân số trước khi thêm (bớt) và sau khi thêm (bớt). Nếu thêm (bớt) ở
tử thì quy đồng mẫu, nếu thêm (bớt) ở mẫu thì quy đồng tử.
- Tìm hiệu (mẫu hoặc tử) giữa hai phân số này để tìm ra chênh lệch.
- Lấy số đơn vị đã thêm (hoặc bớt) chia cho hiệu số phần chênh lệch (của tử số hoặc
mẫu số) để tìm ra giá trị của một phần.
- Lấy giá trị của một phần nhân với cả tử và mẫu của giá trị phân số đã cho (sau khi đã
quy đồng) để tìm phân số đã cho.
Bài 4. Tìm một phân số biết phân số đó có giá trị bằng
2
5
và biết nếu thêm vào tử số
45 đơn vị thì ta được phân số mới có giá trị bằng
13
20
Hướng dẫn
- Quy đồng mẫu
2
5
và
13
20
thành và
8
20
và
13
20
- Hiệu của hai tử số là: 13 – 8 = 5
- Giá trị một phần là: 45 : 5 = 9
- Tử số cần tìm là. 8
9 = 72
- Mẫu số cần tìm là 20
9 = 180
Vậy Phân số cần tìm là:
72
180
Dạng 3.5: Dạng đặc biệt thêm bớt mà không có phân số ban đầu
Quy đồng mẫu nếu thêm ở tử, quy đồng tử nếu thêm vào mẫu
Bài 5. Tìm phân số nếu thêm vào tử 5 đơn vị được phân số có giá trị
3
4
, còn nếu bớt 5
đơn vị ở tử số thì được phân số có giá trị
1
2
Hướng dẫn
Mẫu số không thay đổi ta Quy đồng mẫu
3
4
và
1
2
thành
3
4
và
2
4
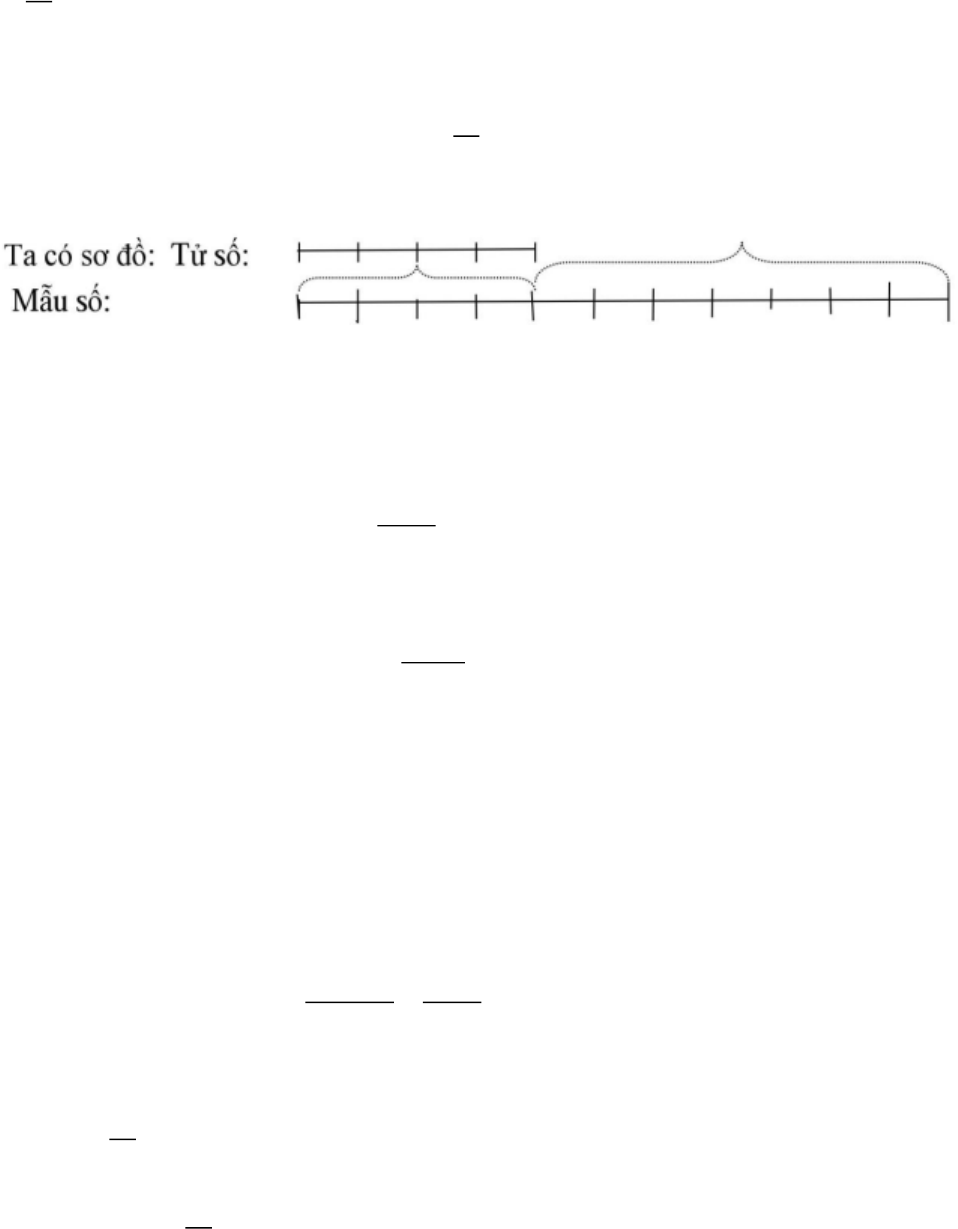
Mẫu số 4 phần
Ta có sơ đồ:
Ta thấy giá trị một phần 5 + 5 = 10
Tử số là: 2 10 + 5 = 25
Mẫu số: 4 10 = 40
Vậy Phân số cần tìm là:
25
40
Dạng 3.6: Dạng tổng hợp
Bài 6. Mẫu số của phân số lớn hơn tử số của phân số đó là 3521. Sau khi rút gọn được
phân số
4
11
.Tìm phân số đó khi chưa rút gọn.
Hướng dẫn
Cách 1: Phân số sau khi rút gọn được phân số
4
11
, ta coi tử số có 4 phần bằng nhau và
mẫu số có 11 phần như thế. 3521
Hiệu số phần bằng nhau là: 11 – 4 = 7 (phần)
Tử số của phân số đó là: 3521 : 7 4 = 2012
Mẫu số của phân số đó là: 3521 + 2012 = 5533
Vậy phân số khi chưa rút gọn là:
2012
5533
Cách 2:
- Phân số khi chưa rút gọn có dạng
4
11
n
n
Theo bài ra ta có: 11 n – 4 n = 3521
(11 – 4) n = 3521
7 n = 3521
n = 3521 : 7
n = 503
Vậy phân số khi chưa rút gọn là:
4 503 2012
11 503 5533
=
Bài 7. Tổng của tử số và mẫu số của một phân số là 4140. Sau khi rút gọn phân số đó
ta được phân số
7
13
. Tìm phân số khi chưa rút gọn.
Khi rút gọn được phân
7
13
, vậy tử số có mấy phần bằng nhau và mẫu có mấy phần như
thế? ( Tử số có 7 phần bằng nhau thì mẫu số có 13 phần như thế)
Hướng dẫn
Cách 1:
Phân số sau khi rút gọn được phân số
7
13
. Coi tử số có 7 phần bằng nhau và mẫu
số là 13 phần như thế.
Tổng số phần bằng nhau là: 7 + 13 = 20 ( phần)
Tử số của phân số là: 4140 : 20 7 = 1449
Mẫu số phân số đó là: 4140 –1449 = 2691
Vậy phân số khi chưa rút gọn là:
1449
2691
Cách 2:
Phân số khi chưa rút gọn có dạng:
7
13
n
n
Theo bài ra ta có: 7 n + 13 n = 4140
(7 + 13) n = 4140
20 n = 4140
n = 4140 : 20
n = 207
Vậy phân số khi chưa rút gọn là:
7 207 1440
13 207 2691
=
Bài 8. Cho phân số
5
11
. Hỏi phải bớt ở tử số bao nhiêu và thêm vào mẫu số bấy nhiêu
để được phân số mới bằng phân số
1
3
Hướng dẫn
Cách 1:
Khi bớt ở tử số và thêm vào mẫu số cùng một số tự nhiên, thì tổng mẫu số và tử
số không thay đổi.
Tổng tử số và mẫu số phân số
5
11
là: 5 + 11 = 16
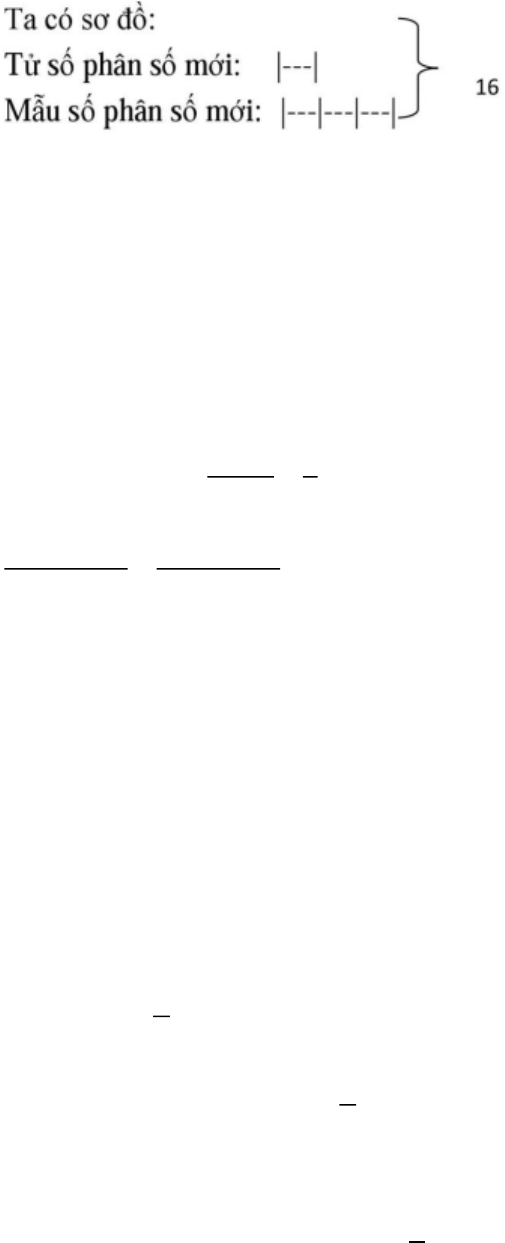
Tổng số phần bằng nhau là: 3 + 1 = 4(phần)
Tử số phân số mới là: 16 : 4 1 = 4
Mẫu số phân số mới là: 5 – 4 = 1
Đáp số: 1
Cách 2:
Gọi số cần bớt ở tử số và thêm vào mẫu số là a.
Theo bài ra ta có:
51
11 3
a
a
−
=
+
( )
( ) ( )
53
11
11 3 3 11
a
a
aa
−
+
=
+ +
(Quy đồng mẫu số hai phân số)
(5 − a)
3 = 11 + a (Hai phân số bằng nhau, mẫu số bằng nhau suy ra tử số
bằng nhau)
15 – 3 a = 11 + a
15 – 11 = a + 3 a
4 = 4 a
a = 1
Vậy số cần tìm là: 1
Bài 9. Cho phân số
7
9
. Hỏi phải thêm vào tử số và mẫu số cùng một số tự nhiên là bao
nhiêu để được phân số bằng phân số
2
3
Hướng dẫn
Cách 1: Hiệu mẫu số và tử số của phân số
7
9
là:19 – 7 = 12
Khi thêm vào tử số và mẫu số của phân số cùng một số tự nhiên thì hiệu trên
không thay đổi.
Ta có sơ đồ:
Hiệu số phần bằng nhau là: 3 – 2 = 1 (phần)
Tử số phân số mới: 12 : 1 2 = 24
Số phải thêm vào tử số và mẫu số là: 24 – 7 = 17
Đáp số: 17
Cách 2:
Gọi số cần tìm thêm vào tử và mẫu số là a.
Theo bài ra ta có:
72
19 3
a
a
+
=
+
( )
( )
( )
( )
7 3 2 19
19 3 3 19
aa
aa
+ +
=
+ +
(Quy đồng mẫu số hai phân số)
(7 + a) 3 = 2 (19 + a)
Hai phân số bằng nhau, mẫu số bằng nhau suy ra tử số bằng nhau
12 + 3 a = 38 + 2 a
21 + a = 38
a = 38 – 21
a = 17. Vậy a = 17
Bài 10. Cho phân số
4
5
a
b
=
. Nếu a cộng thêm 28 , giữ nguyên b thì được phân số mới
bằng phân số
24
23
. Tìm phân số
a
b
Hướng dẫn
Cách 1
Nếu a cộng thêm 28 và giữ nguyên b ta được phân số
28a
b
+
Theo bài ra ta có :
28 24
23
a
b
+
=
28 24
23
a
bb
+=
4 28 24
5 23b
+=
28 24 4
23 5b
=−
28 28
115b
=
b = 115 suy ra
4
115 5
a
=
92
92
115 115
a
a= =
Vậy phân số cần tìm là :
92
115
Cách 2:
Nếu a cộng thêm 28 và giữ nguyên b ta được phân số
28a
b
+
Theo bài ra ta có :
28 24
23
a
b
+
=
28 24 4
23 5
aa
bb
+
− = −
28 28
115
aa
b b b
+ − =
28 28
115
115
b
b
= =
4
115 5
aa
b
==
92
92
115 115
a
a= =
Vậy phân số cần tìm là:
92
115
Bài 11.
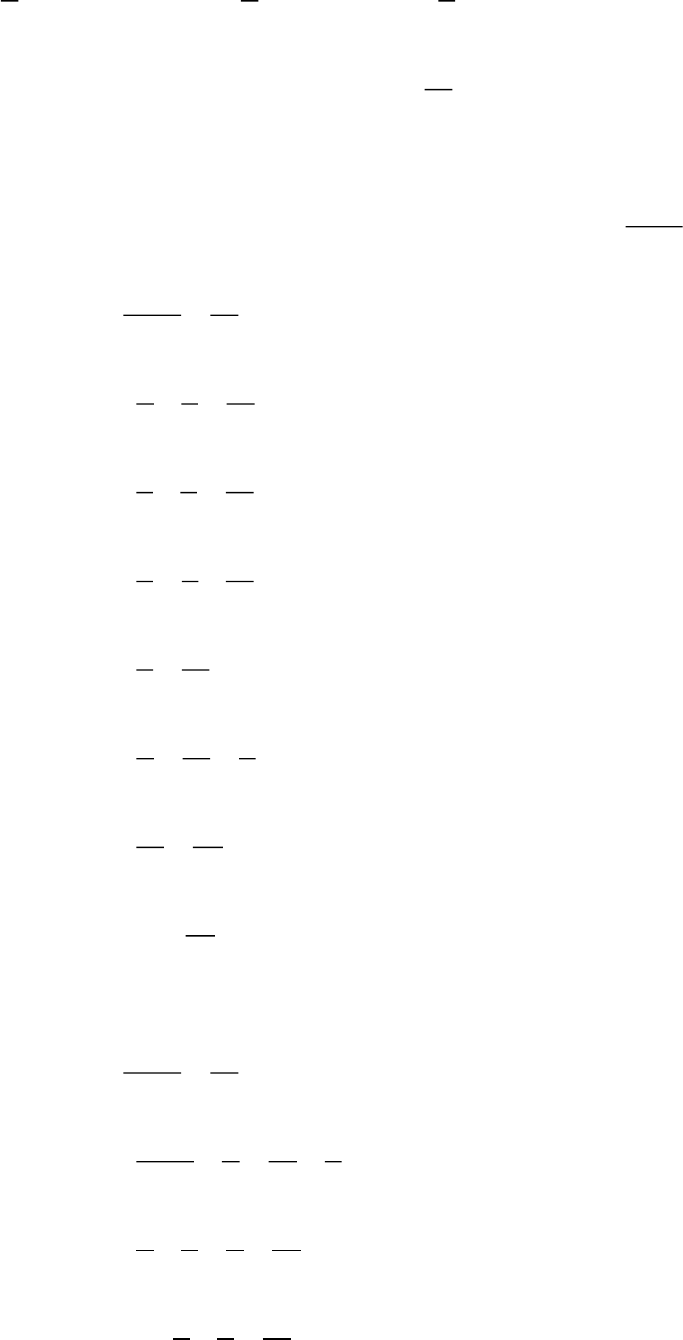
Cho phân số
a
b
. Rút gọn phân số
a
b
được phân số
2
3
. Nếu lấy tử số trừ đi 7 và giữ
nguyên mẫu số thì được phân số mới bằng phân số
9
17
. Tìm phân số đã cho.
Hướng dẫn
Cách 1: Nếu lấy tử số trừ đi 7 và giữ nguyên mẫu số ta được phân số
7a
b
−
Theo bài ra ta có:
79
17
a
b
−
=
79
17
a
bb
−=
2 7 9
3 17b
−=
7 2 9
3 17b
=−
77
51
51
b
b
= =
2
51 3
aa
b
==
34
34
51 51
a
a= =
Vậy phân số cần tìm là:
34
51
Cách 2:
Theo bài ra ta có:
79
17
a
b
−
=
7 9 2
17 3
aa
bb
−
+ = +
7 61
51
aa
b b b
− + =
2 7 61
2
3 51b
− =
3 7 61
4 51b
−=
77
51
51
b
b
= =
2
51 3
aa
b
==
34
34
51 51
a
a= =
Vậy phân số cần tìm là:
34
51
BÀI TẬP TỰ LUYỆN
1. Cho phân số
67
91
. Hãy tìm một số tự nhiên sao cho khi lấy tử số và mẫu số của phân
số đã cho trừ đi số đó ta được phân số có giá trị bằng
1
7
2. Tìm một phân số có tổng tử số và mẫu số là 12, tử số hơn mẫu số 2 đơn vị.
3. Tìm một phân số biết tổng của tử số và mẫu số của phân số đó bằng 154 và biết nếu
thêm vào tử số 18 đơn vị và giữ nguyên mẫu số thì ta được phân số mới có giá trị bằng
1.
4. Cho phân số có tổng của tử số và mẫu số bằng 86. Biết nếu bớt mẫu số đi 7 đơn vị
và thêm vào tử số 7 đơn vị thì ta được phân số mới bằng 1. Tìm phân số đó.
5. Tìm một phân số biết nếu chuyển 8 đơn vị từ mẫu số lên tử số ta được phân số mới
có giá trị bằng 1 và có tổng của tử số và mẫu số bằng 186.
6. Cho phân số
64
107
. Thêm vào tử số của phân số đó a đơn vị và bớt mẫu số đi a đơn
vị ta được phân số mới có giá trị bằng
4
5
. Tìm a.
7. Tìm một phân số biết tổng của tử số và mẫu số của phân số đó bằng 162 và biết phân
số đó có giá trị bằng
4
5
8. Cho phân số
52
91
hỏi cùng phải bớt cả tử số và mẫu số đi bao nhiêu đơn vị để phân
số mới có giá trị bằng
1
2
9. Tìm một phân số biết, nếu thêm vào tử số đó 5 đơn vị và giữ nguyên mẫu số ta được
phân số có giá trị bằng 1 còn nếu chuyển từ tử số xuống mẫu số 1 đơn vị ta được phân
số mới có giá trị bằng
1
2
10.Cho phân số
27
44
. Hỏi phải thêm số tự nhiên nào vào tử số và giữ nguyên mẫu số để
được phân số mới có giá trị bằng
3
4
DẠNG 4: SO SÁNH PHÂN SỐ:
CÁC CÁCH SO SÁNH PHÂN SỐ
* Quy Tắc 1:
- Phân số có tử số nhỏ hơn mẫu số thì phân số đó nhỏ hơn 1.
- Phân số có tử số bằng mẫu số thì phân số đó bằng 1.
- Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
* Quy Tắc 2:
- Hai phân số có cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.
- Hai phân số có cùng tử số: Phân số nào có mẫu số lớn hơn thì nhỏ hơn.
1- So sánh phân số bằng cách quy đồng mẫu số - tử số.
a. Quy đồng mẫu số
Ví dụ: So sánh
1
2
và
1
3
Ta có:
1 1 3 3
2 2 3 6
==
1 1 2 2
3 3 2 6
==
Vì
32
66
nên
11
23
b. Quy đồng tử số:
Ví dụ:
2
5
và
3
4
Ta có:
2 2 3 6
5 5 3 15
==
3 3 2 6
4 4 2 8
==
Vì
66
15 8
nên
23
54
2- So sánh phân số bằng cách so sánh phần bù với đơn vị của phân số
Phần bù với đơn vị của phân số là hiệu giữa 1 và phân số đó.
- Trong hai phân số, phân số nào có phần bù lớn hơn thì phân số đó nhỏ hơn và ngược
lại.
Ví dụ 1: So sánh các phân số sau bằng cách thuận tiện nhất.
2016
2017
và
2017
2018
Bước 1: Tìm phần bù
Ta có:
2016 1
1
2017 2017
−=
2017 1
1
2018 2018
−=
Bước 2: So sánh phần bù với nhau, kết luận 2 phân số cần so sánh.
Vì
11
2017 2018
nên
2016 2017
2017 2018
* Chú ý: đặt A = Mẫu 1 – Tử 1
A = Mẫu 2 – Tử 2
Cách so sánh phần bù được dùng khi A = A. Nếu trong trường hợp A
A ta có thể sử
dụng tính chất cơ bản của phân số để biến đổi đưa về 2 phân số mới có hiệu giữa mẫu
và tử của 2 phân số bằng nhau:
Ví dụ 2:
2016
2017
và
2017
2019
. Ta có
2016 2016 2 4032
2017 2017 2 4034
==
Bước 1: Ta có :
4032 2
1
4034 4034
−=
2017 2
1
2019 2019
−=
Bước 2: Vì
22
4034 2019
nên
4032 2017
4034 2019
hay
2016 2017
2017 2019
3- So sánh phân số bằng cách so sánh phần hơn với đơn vị của các phân số:
- Phần hơn với đơn vị của phân số là hiệu của phân số và 1.
- Trong 2 phân số, phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn.
Ví dụ 1: So sánh:
2017
2016
và
2018
2017
Bước 1: Ta có:
2017 1
1
2016 2016
−=
2018 1
1
2017 2017
−=
Bước 2: So sánh phần hơn của đơn vị, kết luận về 2 phân số cần so sánh
Vì
11
2016 2017
nên
2017 2018
2016 2017
Chú ý: Đặt B = Tử 1 – Mẫu l
B’ = Tử 2 – Mẫu 2
Cách so sánh phần hơn được dùng khi B = B’. Nếu trong trường hợp B
B ta
có thể sử dụng tính chất cơ bản của phân số để biến đổi đưa về 2 phân số mới có hiệu
giữa tử và mẫu của 2 phân số bằng nhau:
Ví dụ 2:
2016
2015
và
2018
2016
Bước 1: Ta có:
2016 2016 2 4032
2015 2015 2 4030
==
4032 2
1
4030 4030
−=
2018 2
1
2016 2016
−=
Bước 2: Vì
22
4030 2016
nên
4032 2018
4030 2016
. Hay
2016 2018
2015 2016
4 – So sánh phân số bằng cách so sánh cả 2 phân số với phân số trung gian
Ví dụ 1: So sánh:
3
5
và
4
9
Bước 1: Ta thấy
3 3 1
5 6 2
=
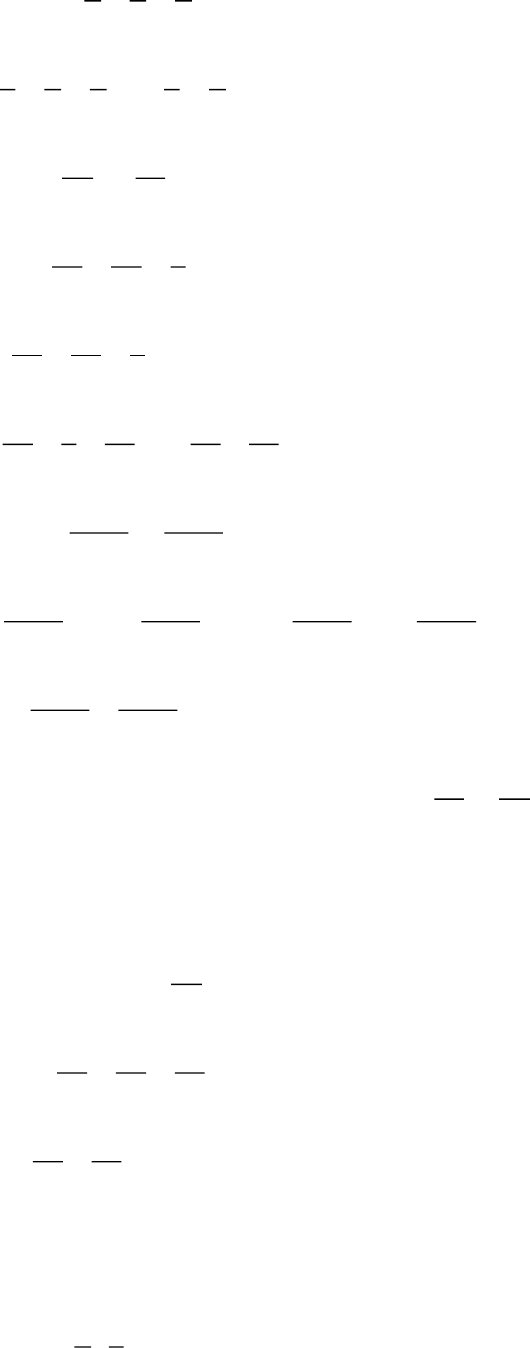
441
9 8 2
=
Bước 2: Vì
3 1 4
529
nên
34
59
Ví dụ 2: So sánh
19
60
và
31
90
Bước 1: Ta thấy
19 20 1
60 60 3
=
31 30 1
90 90 3
=
Bước 2: Vì
19 1 31
60 3 90
nên
19 31
60 90
Ví dụ 3: So sánh:
2017
2016
và
2017
2018
Bước 1: Vì
2017
1
2016
và
2017
1
2018
nên
2017 2017
1
2016 2018
Bước 2: Vậy:
2017 2017
2016 2018
Ví dụ 4: So sánh 2 phân số bằng cách nhanh nhất:
34
75
và
35
74
Chọn một phân số trung gian thứ 3 có cùng tử số với một trong hai phân số đã cho,
cùng mẫu số với phân số còn lại
Chọn phân số trung gian là
34
74
Bước 1: Ta thấy
35 34 34
74 74 75
Bước 2: Vậy :
35 34
74 75
• Cách chọn phân số trung gian.
- Trong một số trường hợp đơn giản có thể chọn phân số trung gian là những phân số
dễ tìm được như :
11
; ;1.......
23
(Ví dụ 1, 2, 3)
- Trong trường hợp tổng quát : So sánh 2 phân số
a
b
và
c
d
( a, b, c, d
0)
Nếu a > c còn b > d thì ta có thể chọn phân số trung gian là
a
d
hoặc
c
b
(như Ví dụ 4).
- Trong trường hợp hiệu của tử số của phân số thứ nhất với tử số của phân số thứ 2 và
hiệu của mẫu phân số thứ nhất với mẫu của phân số thứ 2 gấp nhiều lần tử số và mẫu
số của phân số thương 2 thì ta cùng gấp cả tử số và mẫu số của 2 phân số lên 1 số lần
sao cho hiệu giữa 2 tử số và hiệu giữa 2 mẫu số của 2 phân số là nhỏ nhất. Sau đó ta
tiến hành chọn phân số trung gian như trên.
Ví dụ 5: So sánh 2 phân số bằng cách hợp lý nhất
15
23
và
70
117
Bước 1: Ta có :
15 15 5 75
23 23 5 115
==
Ta so sánh với
70
117
với
75
115
Bước 2 : Chọn phân số trung gian là
70
117
Bước 3: Vì
70 70 75
117 115 115
nên
70 75
117 115
hay
70 15
117 23
5 – Đưa 2 phân số về dạng hỗn số để so sánh
- Khi thực hiện phép chia tử số cho mẫu số của 2 phân số ta được cùng thương và số
dư thì ta đưa 2 phân số cần so sánh về dạng hỗn số rồi so sánh 2 hỗn số đó :
Ví dụ 1: So sánh:
47
15
và
65
21
Ta có:
47 2
3
15 15
=
65 2
3
21 21
=
Vì
22
15 21
nên
22
33
15 21
. Hay
47 65
15 21
Hoặc khi thực hiện phép chia tử số cho mẫu số của 2 phân số ta được 2 thương khác
nhau cũng đưa 2 phân số về hỗn số để so sánh.
Ví dụ 2: So sánh
41
11
và
23
10
Ta có:
41 8
3
11 11
=
23 3
2
10 10
=
Vì 3 > 2 nên
83
32
11 10
hay
41 23
11 10
BÀI TẬP TỰ LUYỆN
1. Số tự nhiên m thoả mãn
57
33
m
là …
2. Cho các phân số :
20 1 11 9
; ; ;
3 6 9 9
. Phân số bé hơn 1 là: …
3. Điền dấu thích hợp vào chỗ chấm:
3
5
…1
4. Số tự nhiên n thoả mãn
58
43
n
là …
5. Điền dấu >; < hoặc = vào chỗ chấm:
7
...1
6
6. Điền dấu >;< hoặc = vào chỗ chấm:
4
5
…1
7. Điền dấu >; < hoặc = vào chỗ chấm:
9
14
…1
8. Điền dấu >; < hoặc = vào chỗ chấm:
8
3
…1
9. Điền dấu ; < hoặc = vào chỗ chấm:
24 3
80 ...
=
10.Tìm số tự nhiên a biết:
11
4 24 3
a
11.Tìm phân số
1
a
biết:
1 1 2
45a
12.Tìm số tự nhiên m biết:
2
1
36
m
13.Tìm số tự nhiên n biết:
7 98
6 48
n
14.Cho biết:
33
5x
. Số các giá trị của x là: …
15.Số tự nhiên a thỏa mãn
5 11
44
a
là a = …
16.Có bao nhiêu phân số a có mẫu số bằng 2 thỏa mãn
29 69
22
a
?
17.Trong các phân số:
2 10 9 5
;;;
5 15 12 9
phân số
2
3
bé hơn phân số nào?
18.Trong các phân số:
27 38 100 13
; ; ;
42 16 75 30
phân số tối giản là phân số nào?
19.Phân số lớn nhất trong các phân số:
1 3 4 5 5 7
; ; ; ; ;
3 5 5 7 8 9
là phân số nào?
20.Phân số bé nhất trong các phân
4 9 26 3
; ; ;
3 7 27 2
là phân số nào?
21.Điền dấu: >; < hoặc = vào chỗ chấm:
14 10
...
33
22.Tìm phân số lớn nhất trong các phân số sau:
2 5 11 16 8 12
; ; ; ; ;
9 9 9 9 9 9
23.Tìm phân số có mẫu số là 7 sao cho phân số đó lớn hơn phân số
2
3
và nhỏ hơn phân
số
5
6
. Trả lời: Tử số của phân số cần tìm là ...
24.Phân số có giá trị bé hơn 1 là:
a)
11
10
; b)
10
9
; c)
10
11
d)
9
8
25.Điền dấu >; < hoặc = vào chỗ chấm:
7 14 14 7
...
22 5 5 22
++
26.Điền dấu >; < hoặc = vào chỗ chấm:
3 5 4 2
...
30 14 7 35
++
27.Điền dấu >; < hoặc = vào chỗ chấm:
8 5 2 7
...
15 12 5 10
++
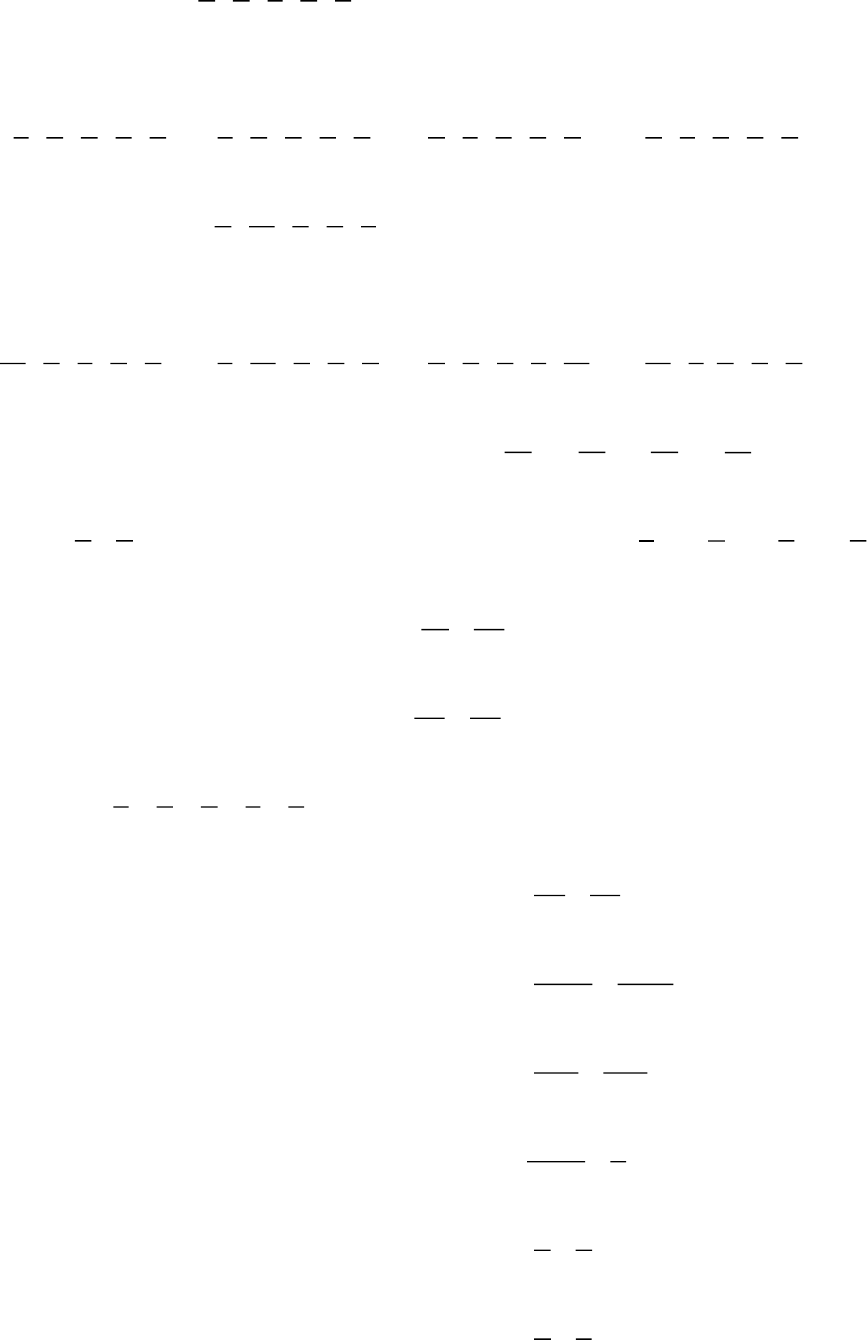
28.Cho các phân số:
2 5 3 7 6
; ; ; ;
3 4 8 5 5
. Các phân số được sắp xếp theo thứ tự tăng
dần là:
a)
3 2 5 6 7
; ; ; ;
8 3 4 5 5
b)
3 2 7 6 5
; ; ; ;
8 3 5 5 4
c)
2 3 6 5 7
; ; ; ;
3 8 5 4 5
d)
2 3 6 7 5
; ; ; ;
3 8 5 5 4
29. Cho các phân số:
3 11 5 2 8
; ; ; ;
4 8 6 9 3
. Các phân số được sắp xếp theo thứ tự giảm dần
là:
a)
11 5 8 2 3
; ; ; ;
8 6 3 9 4
b)
8 11 5 3 2
; ; ; ;
3 8 6 4 9
c)
2 3 5 8 11
; ; ; ;
9 4 6 3 8
d)
11 8 3 5 2
; ; ; ;
8 3 4 6 9
30.Phân số lớn nhất trong các phân số sau là: a)
18
13
;b)
11
15
;c)
14
9
; d)
7
11
31. Biết:
23
...
54
. Phân số thích hợp điền vào chỗ chấm là: a)
1
5
; b)
1
2
; c)
5
6
; d)
4
3
32.Điền dấu >; < hoặc = vào chỗ chấm:
12 22
...
31 21
33.Điền dấu >; < hoặc = vào chỗ chấm:
19 28
...
36 45
34. Cho
1 1 1 1 1
5 6 7 8 9
A = + + + +
. So sánh A với 1
35.Điền dấu >; < hoặc = thích hợp vào chỗ chấm:
47 45
...
52 58
36.Điền dấu >; < hoặc = thích hợp vào chỗ chấm:
2015 1996
...
2011 1992
37.Điền dấu >; < hoặc = thích hợp vào chỗ chấm:
218 218
...
376 367
38.Điền dấu >; < hoặc = thích hợp vào chỗ chấm:
1999 9
...
2003 8
39.Điền dấu >; < hoặc = thích hợp vào chỗ chấm:
53
...
77
40.Điền dấu >; < hoặc = thích hợp vào chỗ chấm:
79
...
55
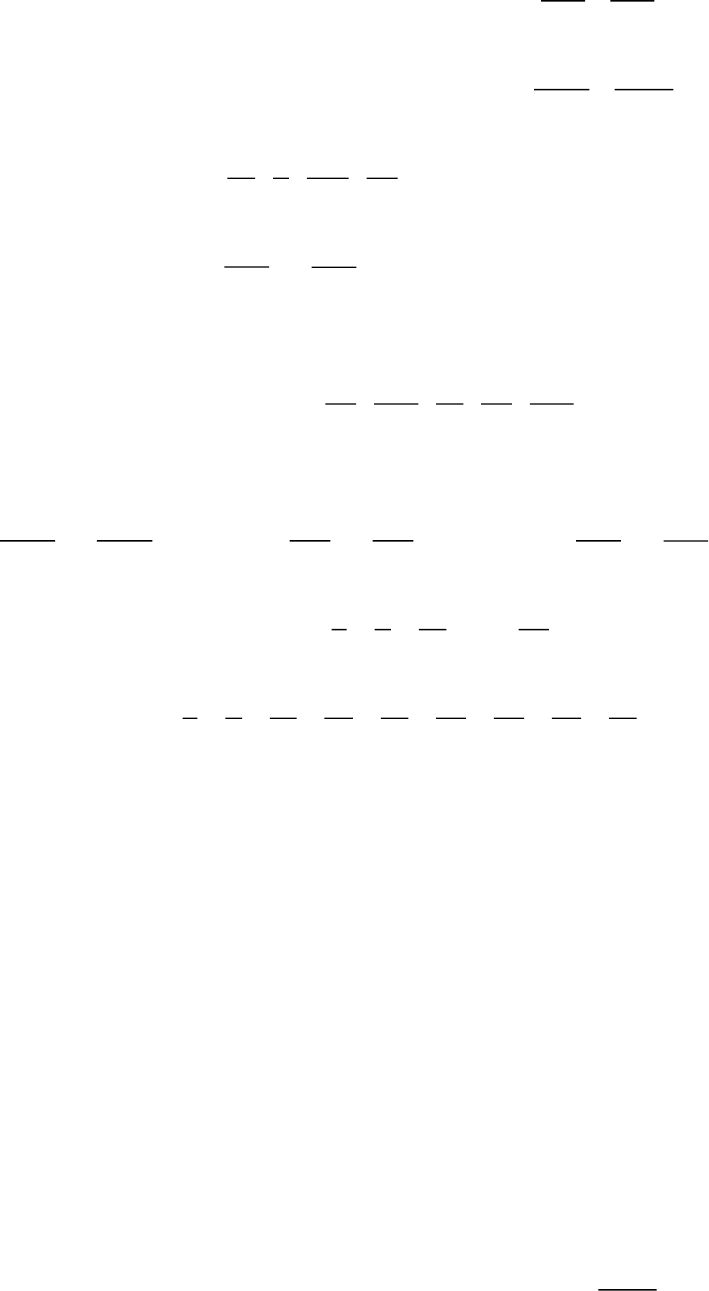
41.Điền dấu > ; < hoặc = thích hợp vào chỗ chấm:
721 721
...
218 215
42.Điền dấu > ; < hoặc = thích hợp vào chỗ chấm:
1998 2015
...
1995 2016
43.Trong các phân số:
15 9 101 29
; ; ;
14 8 100 28
, phân số nào bé nhất?
44.Trong hai phân số:
222
333
và
333
444
phân số nào lớn hơn?
45. Hãy sắp xếp các phân số sau theo thứ tự từ bé đến lớn:
26 215 18 26 162
; ; ; ;
15 253 18 11 253
46. So sánh các cặp phân số sau bằng cách nhanh nhất (Không quy đồng)
a)
1313
1515
và
1326
1428
b)
119
120
và
118
119
c)
222
555
và
333
444
47.So sánh S với 2, biết:
1 1 1 1
1 ...
3 6 10 45
S = + + + + +
48. Chứng tỏ rằng:
1 1 1 1 1 1 1 1 1
1
3 7 13 21 31 43 57 73 91
+ + + + + + + +
DẠNG 5: ĐẾM SỐ CÁC PHÂN SỐ
Dạng 5.1: Đề bài cho một số tìm số các phân số có tổng tử số và mẫu số bằng số
đó:
Loại 1: Số đề bài cho là số lẻ:
Ví dụ 1: Hãy cho biết có tất cả bao nhiêu phân số có tổng tử số và mẫu số bằng 2009
Hướng dẫn
Ta có: 2009 = 0 + 2009 = 1 + 2008 = 2 + 2007 = … = 1004 + 1005
Thấy các cặp (1; 2008), (2; 2007), .. (1004, 1005) mỗi cặp là tạo được 2 phân số khác
nhau và ta có tất cả: 1004 − 1 + 1 = 1004 cặp như vậy.
Riêng cặp (0; 2009) chỉ lập được một phân số là:
0
2009
Do đó, số các phân số có tổng tử số và mẫu số bằng 2009 là:
1004 2 + 1 = 2009 (phân số)
Loại 2: Số đề bài cho là số chẵn
Ví dụ 2: Hãy cho biết có tất cả bao nhiêu phân số có tổng tử số và mẫu số bằng 2008.
Hướng dẫn
Ta có: 2008 = 0 + 2008 = 1 + 2007 = 2 + 2006 = …= 1003 + 1005 = 1004 + 1004.
Thấy các cặp (1; 2007), (2; 2006)... (1003; 1005) mỗi cặp lập được 2 phân số khác
nhau.
Riêng cặp (0; 2008) và (1004; 1004) mỗi cặp chỉ lập được 1 phân số là:
0 1004
;
2008 1004
Số phân số có tổng tử số và mẫu số bằng 2008 là:
1003 2 + 1 + 1 = 2008 (phân số)
Tổng quát: Số phân số bằng số đã cho.
Dạng 5.2: Đề bài cho một số tìm số các phân số có tích tử số và mẫu số bằng phân
số đó:
Ví dụ 3: Hãy cho biết có tất cả bao nhiêu phân số có tích tử số và mẫu số bằng 100?
Hướng dẫn
Ta có: 100 = 1 100 = 2 50 = 4 25 = 5 20 = 10 10
Các cặp (1; 100), (2; 50), (4; 25), (5; 20) mỗi cặp tạo được 2 phân số khác nhau
và ta các tất cả 4 cặp.
Riêng cặp (10; 10) chỉ tạo được một phân số duy nhất.
Số phân số có tích tử số và mẫu số bằng 100 là:
4 2 + 1 = 9 (phân số)
Đ/S: 9 phân số.
Ví dụ 4: Hãy cho biết có tất cả bao nhiêu phân số có tích tử số và mẫu số bằng 1000?
Hướng dẫn
Ta có: 1000 = 1 1000 = 2 500 = 4 250 = 5 200 = 8 125 = 10 100 =
20 50 = 25 40
Thấy có tất cả 8 cặp thừa số có tích là 1000 và mỗi thừa số trong các cặp đều
khác nhau. Do đó, mỗi cặp như vậy tạo được 2 phân số khác nhau.
Số phân số có tích tử số và mẫu số bằng 1000 là: 8 2 = 16 (phân số)
Đ/S: 16 phân số.
Dạng 5.3: Đề bài cho một phân số bắt tìm số các phân số có giá trị bằng phân số
đã cho thỏa mãn một điều kiện nào đó:
Ví dụ 5: Hãy cho biết có tất cả bao nhiêu phân số bằng phân số
2
3
mà tử số và mẫu số
đều là số có 2 chữ số ?
Hướng dẫn
Ta có:
2 10 12 14 16 66
...
3 15 18 21 24 99
= = = = = =
Phân số đầu tiên thỏa mãn đề bài là:
10
15
; phân số cuối cùng thỏa mãn đề bài là:
66
99
Do số phân số = số tử số = số mẫu số.
Thấy các tử số lập thành dãy các đều: 10; 12; 14; 16; ...; 66.
Số phân số thỏa mãn đề bài là: (66 – 10) : 2 + 1 = 29 (phân số)
Đ/S: 29 phân số.
Ví dụ 6: Hãy cho biết có tất cả bao nhiêu phân số bằng phân số
8
32
mà tử số và mẫu số
đều là số có 2 chữ số ?
Hướng dẫn
Thấy:
81
32 4
=
Ta có
1 10 11 12 24
...
4 40 44 48 96
= = = = =
Các tử số của các phân số thỏa mãn đề bài lập thành dãy các đều: 10; 11; 12; …;
24.
Số các phân số bằng
8
32
mà tử số và mẫu số đều là số có 2 chữ số là:
(24 – 10 : 1 + 1 = 15 (phân số)
Đ/S: 15 phân số.
Các bước giải:
B1: Rút gọn phân số đã cho về phân số tối giản.
B2: Tìm phân số có tử số và mẫu số bé nhất bằng phân số đã cho ; phân số có tử số và
mẫu số lớn nhất bằng phân số đã cho thỏa mãn điều kiện đề bài.
Khi đó: các tử số (mẫu số) lập thành một dãy cách đều có khoảng cách là tử số (mẫu
số) của phân số tối giản tìm được ở bước 1.
B3: Đếm số các tử số (mẫu số) thỏa mãn đề bài và kết luận.
Dạng 5.4: Loại khác:
Ví dụ 7: Cho các số từ 0 đến 9. Hỏi có bao nhiêu phân số nhận các số đã cho làm tử số
và mẫu số?
Hướng dẫn
Có 10 cách chọn tử số từ các số 0; 1; 2; ..; 9
Có 9 cách chọn mẫu số từ các số: 1; 2; 3; ..; 9
Số các phân số nhận các số từ 0 đến 9 làm tử số và mẫu số là:
10 9 = 90 (phân số)
Đ/S: 90 phân số.
BÀI TẬP TỰ LUYỆN
1. Có bao nhiêu phân số vừa lớn hơn 1 vừa nhỏ hơn 2 có mẫu số là 3. Trả lời : Có .....
phân số.
2. Có bao nhiêu phân số nhỏ hơn 1 có mẫu số là 4 và có tử số khác 0
3. Hãy cho biết có tất cả bao nhiêu phân số bằng
11
14
mà tử số và mẫu số đều là số có
hai chữ số.
4. Có bao nhiêu phân số lớn hơn 1 có mẫu số bằng 29 và tử số nhỏ hơn 100.
5. Hãy cho biết có bao nhiêu phân số mà tích của tử số và mẫu số của mỗi phân số đó
bằng 70. Số phân số thỏa mãn là: a) 8 ; b) 5 ; c) 10 ; d)12.
6. Hãy cho biết có tất cả bao nhiêu phân số mà tích giữa tử số và mẫu số của mỗi phân
số đó bằng 120?
7. Hãy cho biết có tất cả bao nhiêu phân số mà tử số và mẫu số đều có hai chữ số và
mẫu số hơn tử số 28 đơn vị.
DẠNG 6: TÍNH NHANH TÍNH THUẬN TIỆN VỚI PHÂN SỐ
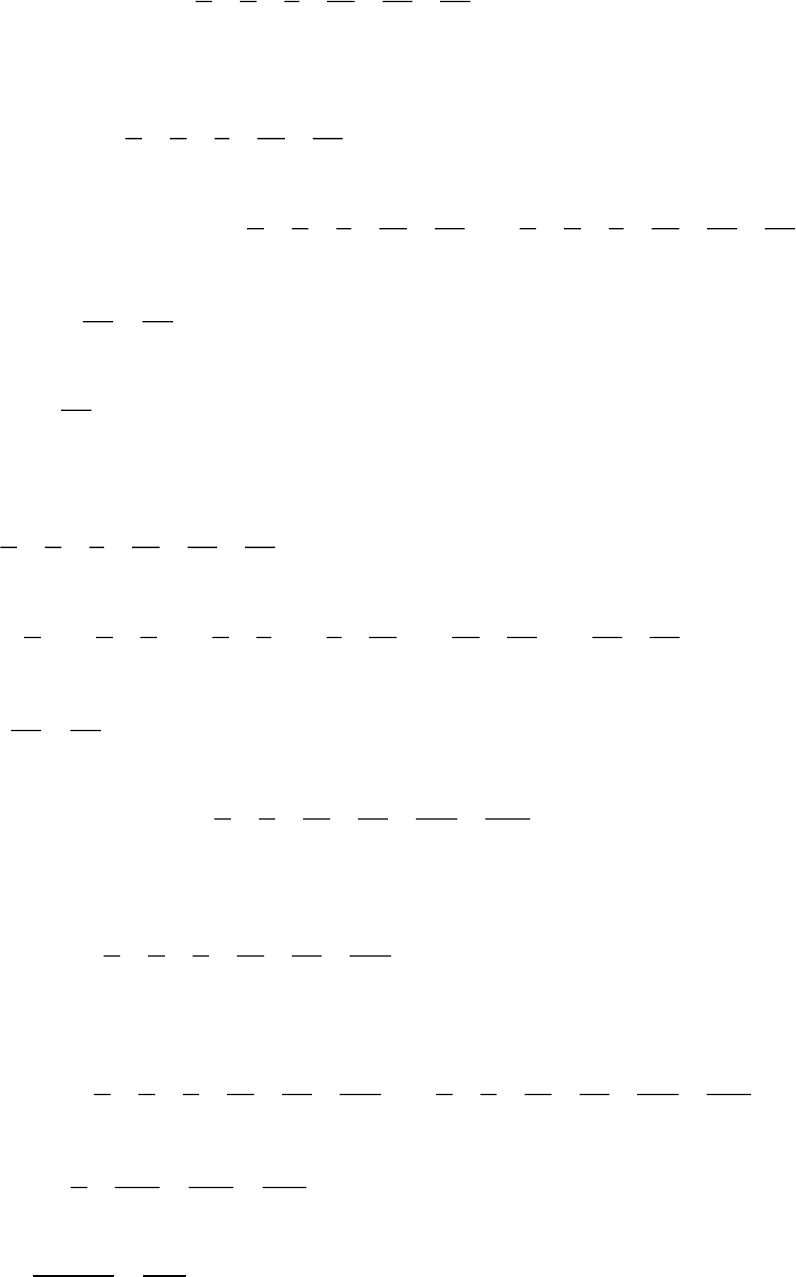
Dạng 6.1: Tính tổng các phân số có cùng tử số và mẫu số của phân số liền sau gấp
mẫu số của phân số liền trước n lần:
VD1: Tính tổng:
1 1 1 1 1 1
2 4 8 16 32 64
A = + + + + +
Hướng dẫn
Tính
1 1 1 1 1
21
2 4 8 16 32
A = + + + + +
Ta có
1 1 1 1 1 1 1 1 1 1 1
21
2 4 8 16 32 2 4 8 16 32 64
A A A
= − = + + + + + − + + + + +
1 63
1
64 64
= − =
Vây
63
64
A =
Cách làm khác:
1 1 1 1 1 1
2 4 8 16 32 64
A = + + + + +
1 1 1 1 1 1 1 1 1 1 1
1
2 2 4 4 8 8 16 16 32 32 64
= − + − + − + − + − + −
1 63
1
64 64
= − =
VD2: Tính nhanh:
1 1 1 1 1 1
2 6 18 54 162 486
A = + + + + +
Hướng dẫn
Tính:
3 1 1 1 1 1
3
2 2 6 18 54 162
A = + + + + +
Ta có:
3 1 1 1 1 1 1 1 1 1 1 1
3
2 2 6 18 54 162 2 6 18 54 162 486
AA
− = + + + + + − + + + + +
3 1 728 364
2
2 486 486 243
A = − = =
364 182
243 2 243
A = =
Vậy
182
243
A =
*TỔNG QUÁT:
...
m m m m m
A
a b c y z
= + + + + +
Trong đó: b = n a; c = n b; … z = n y (n > 0)
Cách giải:
Bước 1: Tính
...
n m n m n m n m
nA
a b c z
= + + + +
...
n m n m n m n m
a n b n c n y
= + + + +
...
n m m m m
a x b y
= + + + +
Bước 2: Tính
... ...
n m m m m m m m m m
n A A
a x b y a b c y z
− = + + + + − + + + + +
( )
1
1
n m m n
n A m
a z a z
− = − = −
1
1
mn
A
n a z
= −
−
Thử lại
VD1:
1 1 1 1 1 1
2 4 8 16 32 64
A = + + + + +
Có: m =1l n = 2; a = 2; z = 64
ADCT:
1 2 1 1 63
11
2 1 2 64 64 64
A
= − = − =
−
VD2:
1 1 1 1 1 1
2 6 18 54 162 486
A = + + + + +
Có: m = 1; n = 2; a = 2; z = 486
ADCT:
1 3 1 182
3 1 2 486 243
A
= − =
−
Dạng 6.2: Tính tổng các phân số có cùng tử số và mẫu số là tích của hai thừa số
trong đó thừa số thứ hai hơn thừa số thứ nhất n đơn vị và thừa số thứ hai của
phân số liền trước là thừa số thứ hai của phân số liền sau:
Tổng:
...
m m m m m
A
a b b c c d x y y z
= + + + + +
Trong đó:b – a = c – b = d – c = … = y – x = z – y = n
VD1: Tính nhanh:
1 1 1 1 1 1
2 6 12 20 30 42
A = + + + + +
Phân tích
Có: 2 = 1 2; 6 = 2 3; 12 = 3 4; 20 = 4 5; 30 = 5 6 và 42 = 6 7
Như vậy
1 1 1 1 1 1
1 2 2 3 3 4 4 5 5 6 6 7
A = + + + + +
Thấy:
1 2 1 2 1
...
1 2 1 2 1 2 1 2
−
= = −
Hướng dẫn
Ta có:
1 1 1 1 1 1
2 6 12 20 30 42
A = + + + + +
1 1 1 1 1 1
1 2 2 3 3 4 4 5 5 6 6 7
A→ = + + + + +
2 1 3 2 4 3 5 4 6 5 7 6
1 2 2 3 3 4 4 5 5 6 6 7
A
− − − − − −
→ = + + + + +
2 1 3 2 4 3 5 4
1 2 1 2 2 3 2 3 3 4 3 4 4 5 4 5
6 5 7 6
5 6 5 6 6 7 6 7
A
→ = − + − + − + − +
− + −
1 1 1 1 1 1 1 1 1 1 1
1
2 2 3 3 4 4 5 5 6 6 7
A
→ = − + − + − + − + − + −
16
1
77
A→ = − =
VD2: Tính nhanh:
4 4 4
...
3 6 6 9 18 21
A = + + +
Hướng dẫn
4 4 4
...
3 6 6 9 18 21
A = + + +
4 3 3 3
...
3 3 6 6 9 18 21
A
→ = + + +
4 1 1 1 1 1 1
...
3 3 6 6 9 18 21
A
→ = − + − + + −
4 1 1 4 6 8
3 3 21 3 21 21
A
→ = − = =
Vậy
8
21
A =
Tổng quát:
...
m m m m m
A
a b b c c d x y y x
= + + + + +
Trong đó: b – a = c – b = d – c = … = y – x = z – y = n
Các giải
11m m n m b a m b a m
a b n a b n a b n a b a b n a b
−
= + = = − = −
11mm
b c n b c
= −
11mm
c d n c d
= −
…
11mm
y z n y z
= −
Cộng lại vế với vế:
1 1 1 1 1 1 1 1 1 1
...
mm
A
n a b b c c d y z n a z
= − + − + − + + − = −
Vậy
11m
A
n a z
= −
Thử lại
VD1:
1 1 1 1 1 1
2 6 12 20 30 42
A = + + + + +
Xác định được: m =1; n = 1; a = 1; b = 7
Vậy
1 1 1 6
1 1 7 7
A
= − =
VD2:
4 4 4
...
3 6 6 9 18 21
A = + + +
Có: m = 4; n = 3; a = 3; z = 21
Vậy
4 1 1 8
3 3 21 21
A
= − =
Dạng 6.3: Tính tổng nhiều phân số có cùng tử số và mẫu số là tích của ba thừa số trong
đó thừa số thứ ba luôn lớn hơn thừa số thứ nhất n đơn vị không đổi; hai thừa số cuối
của phân số liền trước là hai thừa số trước của phân số liền sau.
VD1: Tính
1 1 1
...
1 3 5 3 5 7 17 19 21
A = + + +
Hướng dẫn
Ta có:
1 1 5 1 1 5 1 1 1 1
1 3 5 4 1 3 5 4 1 3 5 1 3 5 4 1 3 3 5
−
= = − = −
1 1 7 3 1 7 3 1 1 1
3 5 7 4 3 5 7 4 3 5 7 3 5 7 4 3 5 5 7
−
= = − = −
…
1 1 1 1
17 19 21 4 17 19 19 21
= −
Cộng vế với vế ta được:
1 1 1 1 1 1 1
...
4 1 3 3 5 3 5 5 7 17 19 19 21
A
= − + − + + −
1 1 1 80
4 1 3 19 21 969
A
= − =
VD2: Tính
5 5 5 5
...
1 5 8 5 8 12 8 12 15 33 36 40
A = + + + +
Hướng dẫn
Ta có:
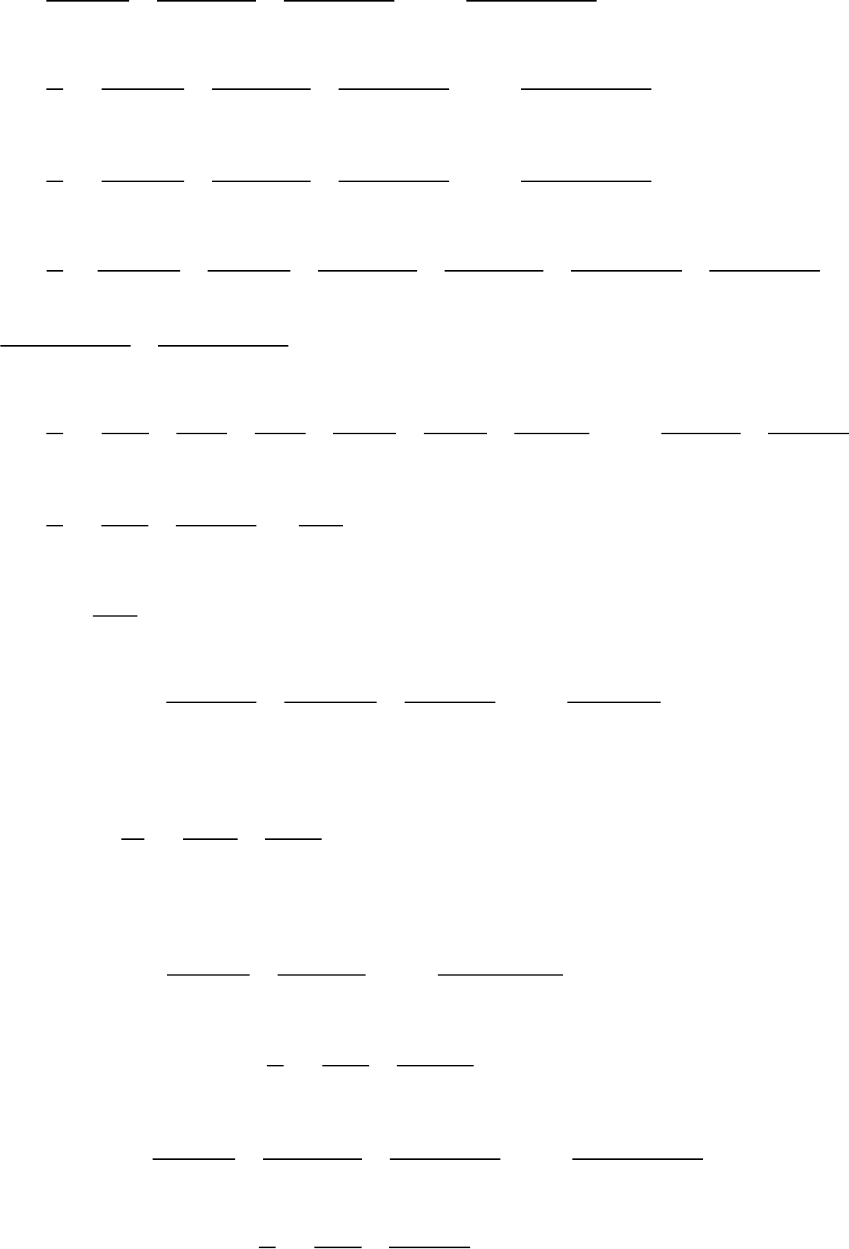
5 5 5 5
...
1 5 8 5 8 12 8 12 15 33 36 40
A = + + + +
5 7 7 7 7
...
7 1 5 8 5 8 12 8 12 15 33 36 40
A
= + + + +
5 8 1 15 5 15 8 40 33
...
7 1 5 8 5 8 12 8 12 15 33 36 40
A
− − − −
= + + + +
5 8 1 12 5 15 8
( ...
7 1 5 8 1 5 8 5 8 12 5 8 12 8 12 15 8 12 15
40 33
)
33 36 40 33 36 40
A = − + − + − + +
−
5 1 1 1 1 1 1 1 1
...
7 1 5 5 8 5 8 8 12 8 12 12 15 33 36 36 40
A
= − + − + − + + −
5 1 1 41
7 1 5 36 40 288
A
= − =
Vậy
41
288
A =
Tổng quát:
...
m m m m
A
a b c b c d c d e x y z
= + + + +
Trong đó: c – a = d – b = e – c = … = z – x = n (n > 0)
Suy ra:
11m
A
n a b y x
= −
Thử lại:
VD1: Tính
1 1 1
...
1 3 5 3 5 7 17 19 21
A = + + +
Có: m = 1; n = 4
1 1 1
4 1 3 19 21
A
= −
VD2: Tính
5 5 5 5
...
1 5 8 5 8 12 8 12 15 33 36 40
A = + + + +
Có m = 5; n = 7
5 1 1
7 1 5 36 40
A
= −
Dạng 6.4: Bài toán tách tử số, mẫu số để thực hiện rút gọn.
VD1: Tính nhanh:
2016 2009 2016 1009
2017 999 1017
A
−
=
+
Hướng dẫn
( )
( )
2016 2009 1009
2016 2009 2016 1009
2017 999 1017 2016 1 999 1017
A
−
−
==
+ + +
2016 1000 2016 1000 2016 1000
1
2016 999 999 1017 2016 999 2016 2016 1000
= = = =
+ + +
Vậy A = 1
VD2: Tính:
2017 2016 1017
1000 2017 2015
−
+
Hướng dẫn
( )
2017 2015 1 1017
2017 2016 1017 2017 2015 2017 1017
1000 2017 2015 1000 2017 2015 1000 2017 2015
+ −
− + −
==
+ + +
2017 2015 1000
1
1000 2017 2015
+
==
+
VD3. Tính
2015 20162016 194519451945
2016 19451945 201520152015
Hướng dẫn
2015 20162016 194519451945 2015 2016 1945
1
2016 19451945 201520152015 2016 1945 2015
= =
VD4: Tính nhanh:
20042004 20052005 20062006 20072007 20082008 20092009
20102010 20112011 20122012 20132013 20142014 20152015
+ + + + +
+ + + + +
Hướng dẫn
Thấy: 20042004 = 10001 2004; 20052005 = 10001 2005; …
Vậy
20042004 20052005 20062006 20072007 20082008 20092009
20102010 20112011 20122012 20132013 20142014 20152015
+ + + + +
+ + + + +
( )
( )
10001 2004 2005 2006 2007 2008 2009
10001 2010 2011 2012 2013 2014 2015
+ + + + +
=
+ + + + +
2004 2005 2006 2007 2008 2009
2010 2011 2012 2013 2014 2015
+ + + + +
=
+ + + + +
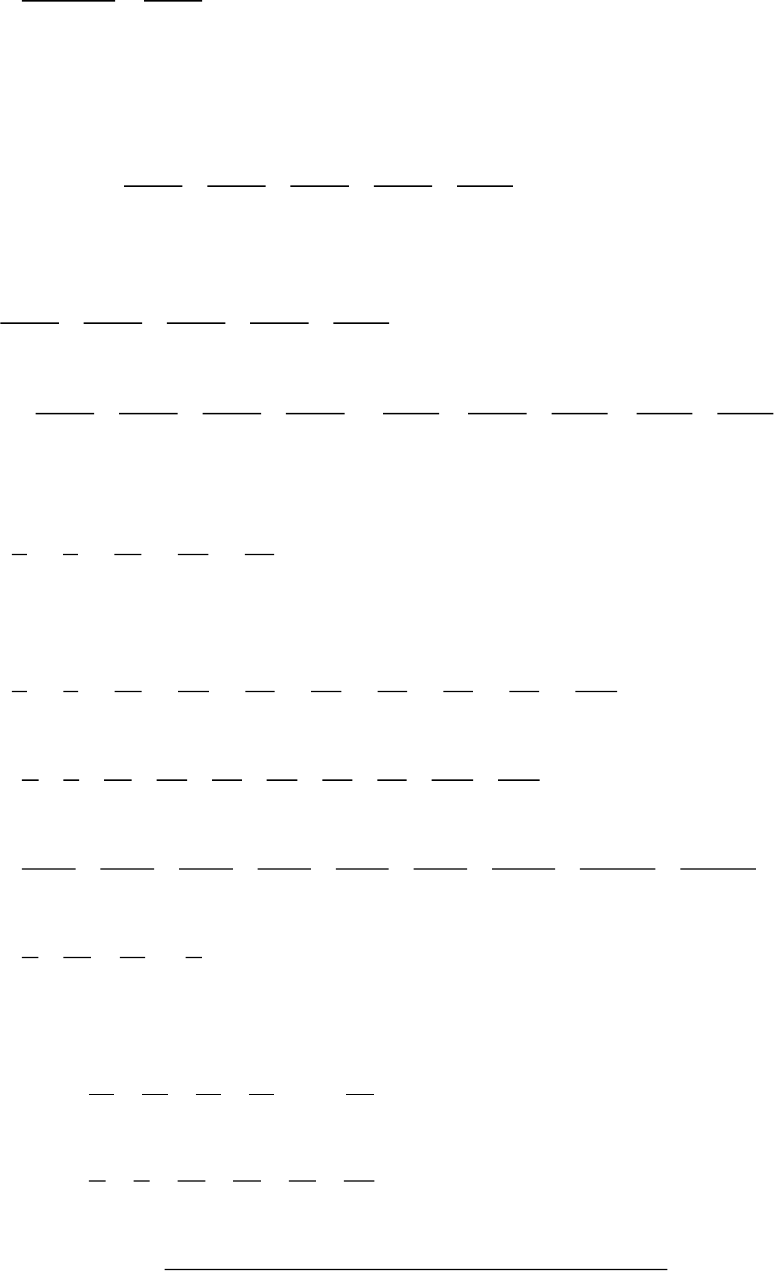
3 4013 4013
3 4025 4025
==
VD1: Tính:
Dạng 6.5: Tính tích nhiều phân số:
VD1: Tính
2011 2012 2013 2014 1005
2010 2011 2012 2013 1007
Hướng dẫn
2011 2012 2013 2014 1005
2010 2011 2012 2013 1007
2011 2012 2013 2014 1005 2014 1005 1007 1005
1
2010 2011 2012 2013 1007 2010 1007 1005 1007
= = = =
VD2: Tính tích 10 hỗn số đầu tiên trong dãy các hỗn số sau:
1 1 1 1 1
1 1 1 1 1 ...
3 8 15 24 35
Giải
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
3 8 15 24 35 48 63 80 99 120
4 9 16 25 36 49 64 81 100 121
3 8 15 24 35 48 63 80 99 120
=
2 2 3 3 4 4 5 5 6 6 7 7 8 8 10 10 11 11
1 3 2 4 3 5 4 6 5 7 6 8 8 10 9 11 10 12
=
2 11 11 5
1
1 12 6 6
= = =
BÀI TẬP TỰ LUYỆN
1. Tính:
1 2 3 4 10
... ...
11 11 11 11 11
+ + + + + =
2. Tính:
1 3 5 7 9 11
2 6 10 14 18 22
+ + + + + =
3. Tính nhanh:
1 3 5 2 6 10 4 12 20 7 21 35
1 5 7 2 10 14 4 20 28 7 35 49
+ + +
+ + +
4. Tính nhanh:
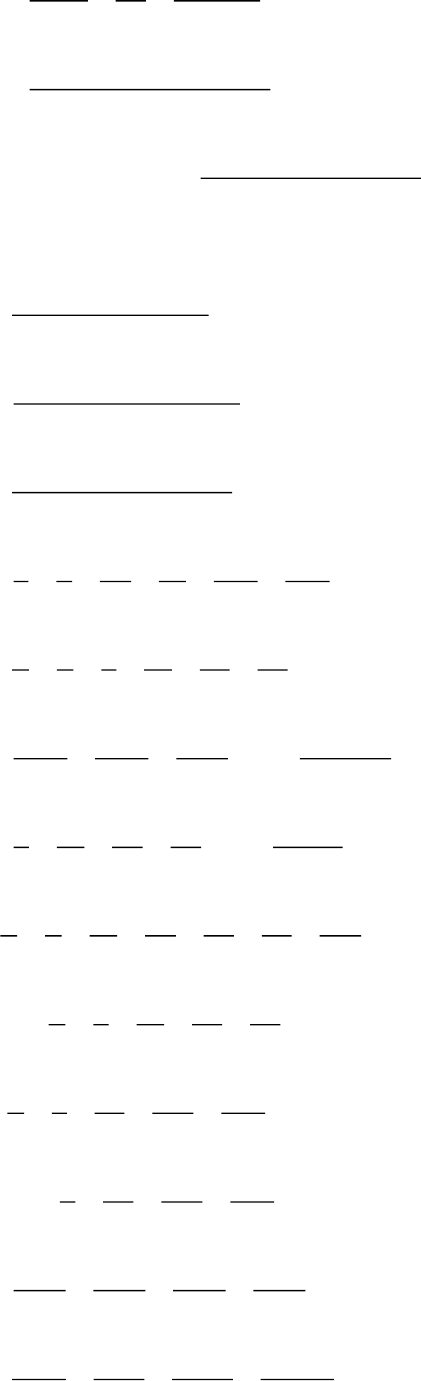
3333 36 666666
4545 45 454545
A = + +
10 32 54 76 98
12 36 54 78 90
B
+ + + +
==
++++
5. Tính nhanh:
2005 2007 1
2004 2005 2006
A
−
=
+
6. Tính nhanh:
a)
64 50 100 44
27 38 146 19
+
+
b)
155 818 45 182
999 77 301 23
+ + +
− + −
c)
2007 2006 1
2005 2007 2006
−
+
d)
1 1 1 1 1 1
3 9 27 81 243 729
+ + + + +
e)
1 1 1 1 1 1
2 4 8 16 32 64
+ + + + +
g)
1 1 1 1
...
2 4 4 6 6 8 98 100
+ + + +
h)
1 1 1 1 1
...
5 10 20 40 12800
+ + + + +
i)
2 2 2 2 2 2 2
3 6 12 24 48 96 192
+ + + + + +
k)
5 5 5 5 5
1
4 8 16 32 64
+ + + + +
l)
3 3 3 3 3
2 8 32 128 512
+ + + +
m)
3 3 3 3
3
5 25 125 625
+ + + +
n)
1 1 1 1
2 3 3 4 4 5 5 6
+ + +
e)
3 3 3 3
2 2 5 8 8 11 11 14
+ + +
o)
4 4 4 4 4 4
3 7 7 11 11 15 15 18 19 23 23 27
+ + + + +
p)
4 4 4 4
3 6 6 9 9 12 12 15
+ + +
q)
2 2 2 2 2 2 2 2
... ...
3 5 5 7 7 9 13 15 1 2 2 3 8 9 9 10
+ + + + + + + + +
r)
7 7 7 7 7
1 5 5 9 9 13 13 17 17 21
+ + + +
7. Tính nhanh:
5 11 19 29 41 55 71 89
6 12 20 30 42 56 72 90
+ + + + + + +
DẠNG 7: TỈ SỐ - TỈ LỆ BẢN ĐỒ VÀ ỨNG DỤNG
1. TỈ SỐ:
- Tỉ số giữa a và b là: a : b hay
a
b
(b
0)
- Tỉ số giữa b và a là: b : a hay
b
a
(a
0)
VD: Trong hộp có 7 viên bi màu vàng và 13 viên bi màu xanh. Tỉ số số bi màu vàng
và số bi màu xanh là: 7 : 13 =
7
13
Tỉ số số bi màu xanh và số bi màu vàng là: 13 : 7 =
13
7
Hay có thể nói:
- Số bi màu vàng bằng
7
13
số bi màu xanh.
- Số bi màu xanh bằng
13
7
số bi màu vàng.
* Dạng toán:
- Tìm hai số khi biết tổng và tỉ.
- Tìm hai số khi biết hiệu và tỉ.
- Bài toán công việc chung (tỉ lệ thuận – tỉ lệ nghịch).
2. TỈ LỆ BẢN ĐỒ - ỨNG DỤNG:
- Tỉ lệ bản đồ là tỉ số giữa chiều dài đo được trên bản đồ và chiều dài thật.
VD: Bản đồ Hà Nội được vẽ với tỉ lệ 1 : 1 000 000 hay
1
1000000
cho chúng ta biết là
thành phố Hà Nội được vẽ thu nhỏ lại 1 000 000 lần.
Khi đó độ dài 1 cm trên bản đồ thì thực tế dài 1 000 000 cm hay 100 km.
- Tỉ lệ bản đồ được viết dưới dạng phân số có tử số là 1.
VD:
1 1 1
; ; ;...
100 1000 5000000
- Muốn tìm chiều dài thật: Chiều dài trên bản đồ chia cho tỉ lệ bản đồ.
VD: Trên một bản đồ tỉ lệ 1 : 500, chiều dài sân trường em là 12 cm. Tính chiều dài
thật của sân trường với đơn vị là mét ?
Hướng dẫn
Chiều dài sân trường em là: 12 :
1
500
= 6 000 cm = 60 (m)
Đ/S: 60 (m)
- Muốn tìm chiều dài trên bản đồ: Lấy chiều dài thật nhân với tỉ lệ bản đồ.
VD: Đường cao tốc Hà Nội – Hải Phòng dài 105km. Hãy cho biết đoạn đường đó được
vẽ trên bản đồ tỉ lệ
1
50000
dài bao nhiêu cm?
Hướng dẫn
Đổi 105 km = 10 500 000 cm.
Chiều dài trên bản đồ của tuyến đường cao tốc Hà Nội – Hải Phòng là:
10 500 000
1
50000
= 21 (cm)
Đ/S: 21 cm.
- Muốn tính tỉ lệ bản đồ: Lấy chiều dài trên bản đồ chia cho chiều dài thực tế (phải
cùng một đơn vị đo)
VD: Quãng đường Hà Nội – Sài Gòn dài 1730km khi vẽ trên một bản đồ dài 173mm.
Tính tỉ lệ bản đồ đó?
Hướng dẫn
Đổi: 1730km = 1 730 000 000 mm.
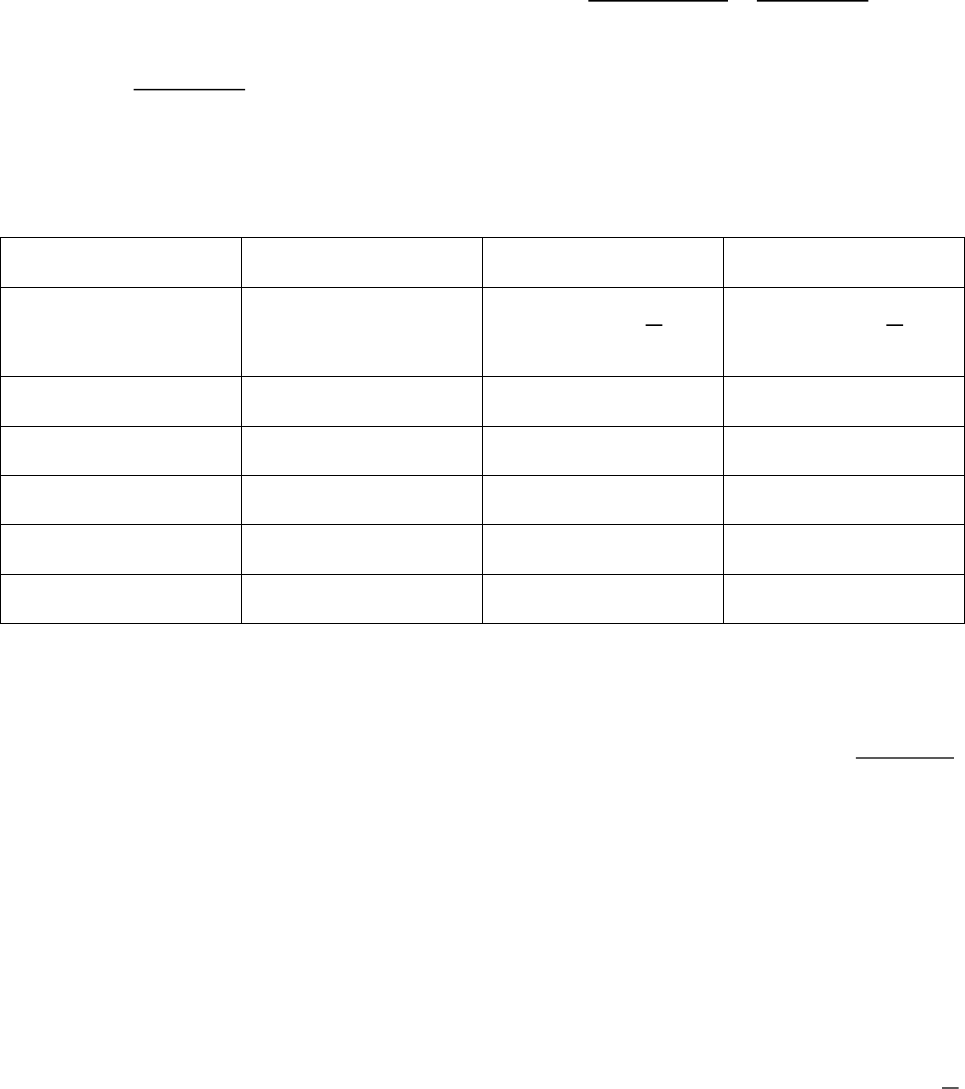
Tỉ lệ của bản đồ đó là: 173 : 1 730 000 000 =
173 1
1730000000 10000000
=
Đ/S:
1
10000000
Bài tập tự luyện
Bài 1. Điền số thích hợp vào ô trống (theo mẫu):
a
b
Tỉ số của a và b
Tỉ số của b và a
5
7
5 : 7 hay
5
7
7 : 5 hay
7
5
7
11
123
97
2014
2017
52
57
6
3
Bài 2. Trên bản đồ vẽ theo tỉ lệ 1 : 500, khoảng cách đo được từ điểm A đến điểm B là
3 cm. Hỏi thực tế khoảng cách từ điểm A đến điểm B là bao nhiêu mét?
Bài 3. Quãng đường từ tỉnh A sang tỉnh B dài 150km. Trên bản đồ tỉ lệ
1
1000000
,
quãng đường đó dài bao nhiêu cm?
Bài 4. Cho hai số 13 và 52. Hãy tìm tỉ số giữa:
a) 13 và 52.
b) 52 và 13.
c) 52 và tổng của hai số đó.
Bài 5. Lớp 5A có 21 bạn nữ. Biết tỉ số giữa số bạn nam và số bạn nữ của lớp 5A là
5
7
. Hỏi lớp 5A có bao nhiêu bạn?
Bài 6. May 5 áo sơ mi hết 10m vải. Hỏi may 23 áo sơ mi như thế hết bao nhiêu mét
vải?
Bài 7. Trong một buổi sinh hoạt Đội, tỉ số bạn nam và bạn nữ là
3
8
. Hỏi nếu giảm số
bạn nữ xuống 2 lần và gấp số bạn nam lên 4 lần thì tỉ số bạn nam và bạn nữ khi đó là
bao nhiêu? (kết quả viết dưới dạng phân số tối giản)
Bài 8. Tuổi bố gấp 3 lần tuổi anh, tuổi anh gấp 2 lần tuổi em. Biết tuổi bố cộng với tuổi
em là 42 tuổi. Tính tuổi anh?
Bài 9.
3
4
số cam bằng
2
5
số quýt. Tính tỉ số giữa số cam và số quýt.
Bài 10. Tổng của hai phân số là
8
7
. Tìm hai phân số biết phân số thứ nhất bằng
3
5
phân
số thứ hai?
Bài 11. Một đàn gia súc gồm một số trâu, bò, ngựa. Biết rằng
2
3
số trâu thì bằng
3
7
số
bò và cũng bằng
5
8
số ngựa. Hỏi:
a) Số trâu bằng mấy phần số ngựa?
b) Số ngựa bằng mấy phần số bò?
c) Số bò bằng mấy phần tổng số đàn gia súc?
(Viết kết quả dưới dạng phân số tối giản)
Bài 12. Bạn Lan mua vở hết
1
4
số tiền của mình có. Bạn Phượng mua sách hết
2
7
số
tiền của mình có. Biết rằng số tiền còn lại của hai bạn bằng nhau. Tính tỉ số giữa số
tiền của Lan và Phượng có lúc đầu ? (Viết kết quả dưới dạng phân số tối giản)
Bài 13. Tổng của hai số là 2017. Thương của chúng là 7 dư 1. Tìm số lớn?
Bài 14. Một cái sân hình chữ nhật trên bản đồ có chiều dài là: 5cm, chiều rộng là 3cm.
Tính diện tích cái sân ngoài thực tế. Biết tỉ lệ lệ bản đồ là: 1 : 1000
Nhắn tin Zalo