ƠNG V ĐẠI SỐ TỔ HỢP CHƯ
BÀI 1: QUY TẮC CỘNG. QUY TẮC NHÂN. SƠ ĐỒ HÌNH CÂY LÝ THUYẾT. I = 1. Quy tắc cộng Quy tắc cộng
Giả sử một công việc nào đó có thể thực hiện theo một
trong hai phương án khác nhau:
Phương án 1.. n cách 1
- Phương án 1 có n cách thực hiện. 1
- Phương án 2 có n cách thực hiện.
Phương án 2 .. n cách 2 2
Khi đó số cách thực hiện công việc là : n + n cách 1 2
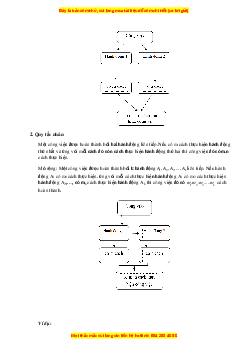
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách
thực hiên, hành động kia có n cách thực hiên không trùng với bất kì cách nào của hành động
thứ nhất thì công việc đó có m + n cách thực hiện.
Chú ý: số phần tử của tập hợp hữu hạn X được kí hiệu là X hoặc n ( X ) .
Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp
hữu hạn không giao nhau: Nếu A và B là các tập hợp hữu hạn không giao nhau thì
n( A B) = n( A) + n(B)
Mở rộng: Một công việc được hoàn thành bởi một trong k hành động
A , A , A ,..., A .Nếu hành động A 1 2 3 k
1 có m1cách thực hiện, hành động A2 có m2 cách thực
hiện,…, hành động Ak có mk cách thực hiện và các cách thực hiên của các hành động trên
không trùng nhau thì công việc đó có m + m + m + ... + m cách thực hiện. 1 2 3 k
2. Quy tắc nhân
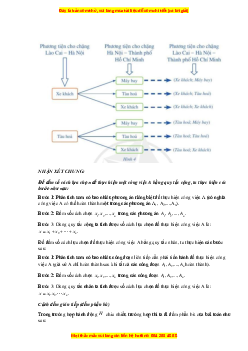
Một công việc được hoàn thành bởi hai hành động liên tiếp.Nếu có m cách thực hiện hành động
thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì công việc đó có m.n cách thực hiện.
Mở rộng: Một công việc được hoàn thành bởi k hành động A , A , A ,..., A liên tiếp. Nếu hành 1 2 3 k
động A1 có m1cách thực hiện, ứng với mỗi cách thực hiện hành động A1 có m2 cách thực hiện
hành động A2,…, có mk cách thực hiện hành động Ak thì công việc đó có m .m .m .....m cách 1 2 3 k hoàn thành. Ví dụ:
NHẬN XÉT CHUNG:
Để đếm số cách lựa chọn để thực hiện một công việc A bằng quy tắc cộng, ta thực hiện các bước như sau:
Bước 1: Phân tích xem có bao nhiêu phương án riêng biệt để thực hiện công việc A (có nghĩa
công việc A có thể hoàn thành một trong các phương án A1, A2,...,An).
Bước 2: Đếm số cách chọn x , x ,..., x trong các phương án A , A ,..., A . 1 2 n 1 2 n
Bước 3: Dùng quy tắc cộng ta tính được số cách lựa chọn để thực hiện công việc A là:
x = x + x + + x . 1 2 n
Để đếm số cách lựa chọn để thực hiện công việc A bằng quy tắc nhân, ta thực hiện các bước sau:
Bước 1: Phân tích xem có bao nhiêu công đoạn liên tiếp cần phải tiến hành để thực hiện công
việc A (giả sử A chỉ hoàn thành sau khi tất cả các công đoạn A , A ,..., A hoàn thành). 1 2 n
Bước 2: Đếm số cách chọn x , x ,..., x trong các công đoạn A , A ,..., A . 1 2 n 1 2 n
Bước 3: Dùng quy tắc nhân ta tính được số cách lựa chọn để thực hiện công việc A là:
x = x .x ..x . 1 2 n
Cách đếm gián tiếp (đếm phần bù)
Trong trường hợp hành động H chia nhiều trường hợp thì ta đi đếm phần bù của bài toán như sau:
• Đếm số phương án thực hiện hành động H (không cần quan tâm đến có thỏa tính chất T hay
không) ta được a phương án.
• Đếm số phương án thực hiện hành động H không thỏa tính chất T ta được b phương án.
Khi đó số phương án thỏa yêu cầu bài toán là: a − b .
3. Sơ đồ hình cây BÀI TẬP.
Câu 1. Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau).
Vẽ sơ đồ hình cây minh họa và cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Câu 2. Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì ghi lại kết quả sấp hay ngửa. Hỏi nếu
người đó gieo ba lần thì có thể có bao nhiêu khả năng xảy ra?
Câu 3. Ở một loài thực vật, A là gen trội quy định tình trạng hoa kép, a là gen lặn quy định tình trạng hoa đơn.
a) Sự tổ hợp giữa hai gen trên tạo ra mấy kiểu gen?
b) Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gen đó?
Câu 4. Có bao nhiêu số tự nhiên
a) có ba chữ số khác nhau?
b) là số lẻ có ba chữ số khác nhau?
c) là số có ba chữ số và chia hết cho 5?
d) là số có ba chữ số khác nhau và chia hết cho 5?
Câu 5. a) Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kí tự là một chữ số. Hỏi
có thể tạo được bao nhiêu mật khẩu khác nhau?
Chuyên đề dạy thêm Toán 10 Học kì 2 Cánh diều
599
300 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Chuyên đề dạy thêm Toán 10 Cánh diều nhằm giúp Giáo viên có thêm tài liệu tham khảo tài liệu môn Toán 10 Cánh diều.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(599 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 10
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
BÀI 1: QUY TẮC CỘNG. QUY TẮC NHÂN. SƠ ĐỒ HÌNH CÂY
1. Quy tắc cộng
Quy tắc cộng
Giả sử một công việc nào đó có thể thực hiện theo một
trong hai phương án khác nhau:
- Phương án 1 có
1
n
cách thực hiện.
- Phương án 2 có
2
n
cách thực hiện.
Khi đó số cách thực hiện công việc là :
12
nn+
cách
Phương án 1..
1
n
cách
Phương án 2 ..
2
n
cách
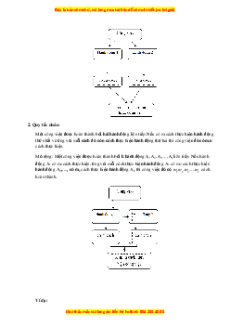
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách
thực hiên, hành động kia có n cách thực hiên không trùng với bất kì cách nào của hành động
thứ nhất thì công việc đó có m + n cách thực hiện.
Chú ý: số phần tử của tập hợp hữu hạn X được kí hiệu là
X
hoặc
( )
nX
.
Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp
hữu hạn không giao nhau: Nếu A và B là các tập hợp hữu hạn không giao nhau thì
( ) ( ) ( )
n A B n A n B = +
Mở rộng: Một công việc được hoàn thành bởi một trong k hành động
1 2 3
, , ,...,
k
A A A A
.Nếu hành động A
1
có m
1
cách thực hiện, hành động A
2
có m
2
cách thực
hiện,…, hành động A
k
có m
k
cách thực hiện và các cách thực hiên của các hành động trên
không trùng nhau thì công việc đó có
1 2 3
...
k
m m m m+ + + +
cách thực hiện.
CHƯƠNG
V
ĐẠI SỐ TỔ HỢP
LÝ THUYẾT.
I
=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
2. Quy tắc nhân
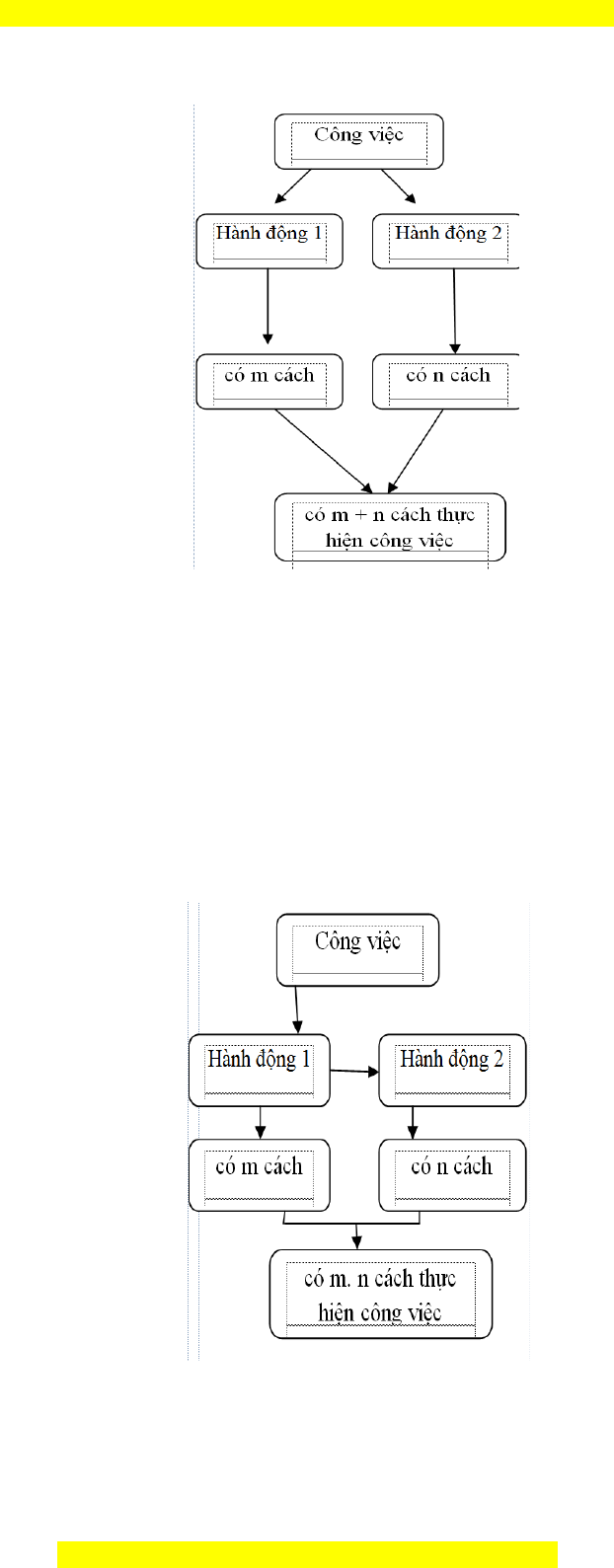
Một công việc được hoàn thành bởi hai hành động liên tiếp.Nếu có m cách thực hiện hành động
thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì công việc đó có m.n
cách thực hiện.
Mở rộng: Một công việc được hoàn thành bởi k hành động
1 2 3
, , ,...,
k
A A A A
liên tiếp. Nếu hành
động A
1
có m
1
cách thực hiện, ứng với mỗi cách thực hiện hành động A
1
có m
2
cách thực hiện
hành động A
2
,…, có m
k
cách thực hiện hành động A
k
thì công việc đó có
1 2 3
. . .....
k
m m m m
cách
hoàn thành.
Ví dụ:
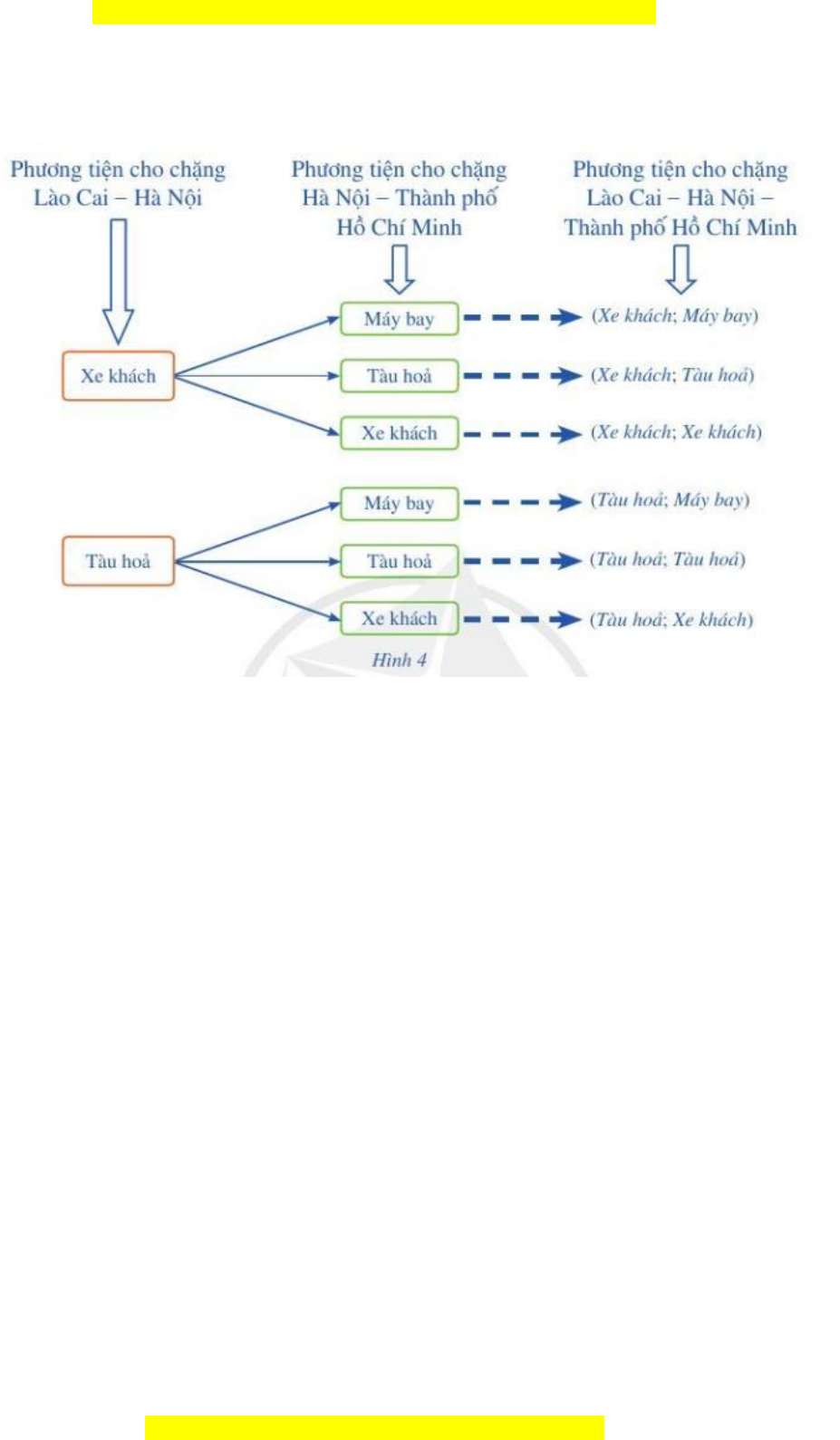
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
NHẬN XÉT CHUNG:
Để đếm số cách lựa chọn để thực hiện một công việc A bằng quy tắc cộng, ta thực hiện các
bước như sau:
Bước 1: Phân tích xem có bao nhiêu phương án riêng biệt để thực hiện công việc A (có nghĩa
công việc A có thể hoàn thành một trong các phương án A
1
, A
2
,...,A
n
).
Bước 2: Đếm số cách chọn
12
, ,...,
n
x x x
trong các phương án
12
, ,...,
n
A A A
.
Bước 3: Dùng quy tắc cộng ta tính được số cách lựa chọn để thực hiện công việc A là:
12 n
x x x x= + + +
.
Để đếm số cách lựa chọn để thực hiện công việc A bằng quy tắc nhân, ta thực hiện các bước
sau:
Bước 1: Phân tích xem có bao nhiêu công đoạn liên tiếp cần phải tiến hành để thực hiện công
việc A (giả sử A chỉ hoàn thành sau khi tất cả các công đoạn
12
, ,...,
n
A A A
hoàn thành).
Bước 2: Đếm số cách chọn
12
, ,...,
n
x x x
trong các công đoạn
12
, ,...,
n
A A A
.
Bước 3: Dùng quy tắc nhân ta tính được số cách lựa chọn để thực hiện công việc A là:
12
. . .
n
x x x x=
.
Cách đếm gián tiếp (đếm phần bù)
Trong trường hợp hành động
H
chia nhiều trường hợp thì ta đi đếm phần bù của bài toán như
sau:
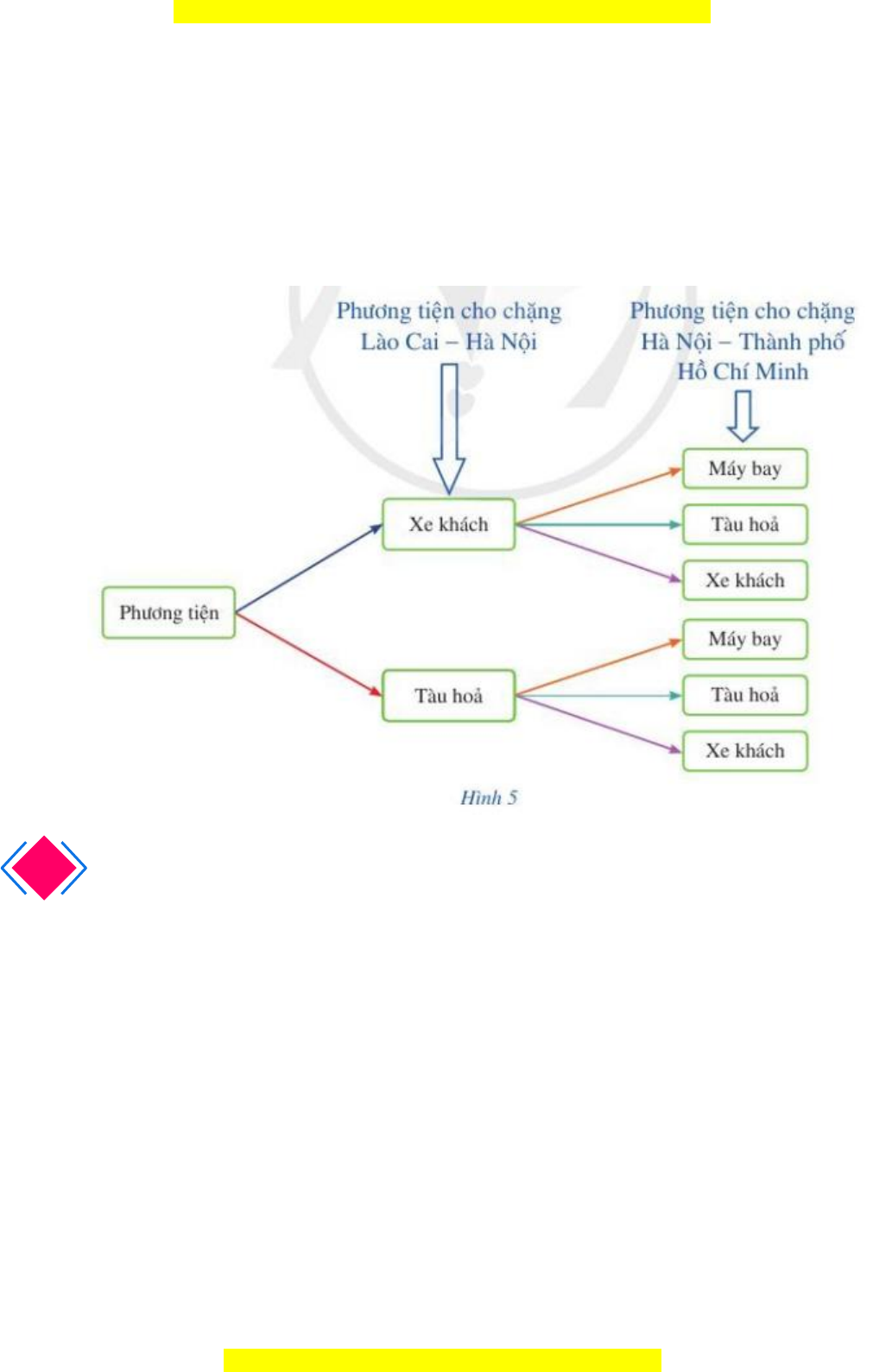
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
•
Đếm số phương án thực hiện hành động
H
(không cần quan tâm đến có thỏa tính chất
T
hay
không) ta được
a
phương án.
•
Đếm số phương án thực hiện hành động
H
không thỏa tính chất
T
ta được
b
phương án.
Khi đó số phương án thỏa yêu cầu bài toán là:
ab−
.
3. Sơ đồ hình cây
Câu 1. Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau).
Vẽ sơ đồ hình cây minh họa và cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc
vào ngày cuối tuần.
Câu 2. Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì ghi lại kết quả sấp hay ngửa. Hỏi nếu
người đó gieo ba lần thì có thể có bao nhiêu khả năng xảy ra?
Câu 3. Ở một loài thực vật, A là gen trội quy định tình trạng hoa kép, a là gen lặn quy định tình
trạng hoa đơn.
a) Sự tổ hợp giữa hai gen trên tạo ra mấy kiểu gen?
b) Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gen đó?
Câu 4. Có bao nhiêu số tự nhiên
a) có ba chữ số khác nhau?
b) là số lẻ có ba chữ số khác nhau?
c) là số có ba chữ số và chia hết cho 5?
d) là số có ba chữ số khác nhau và chia hết cho 5?
Câu 5. a) Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kí tự là một chữ số. Hỏi
có thể tạo được bao nhiêu mật khẩu khác nhau?
BÀI TẬP.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
b) Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên
phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau
là các chữ số (từ 0 đến 9). Hỏi quy định mới có thể tạo được nhiều hơn quy định cũ bao nhiêu
mật khẩu khác nhau?
DẠNG 1: QUY TẮC CỘNG
Nếu một công việc nào nó c th thc hin theo n hưng khc nhau, trong đó:
Hướng thứ 1 có m
1
cách thực hiện
Hướng thứ 2 có m
2
cách thực hiện
…. ……….
Hướng thứ n có m
n
cách thực hiện
Khi đó, có:
12
...
n
m m m+ + +
cách để hoàn thành công việc đ cho.
Câu 1. Giả sử bạn muốn mua một áo sơ mi cỡ
39
hoặc cỡ
40.
Áo cỡ
39
có
5
màu khác nhau, áo cỡ
40
có
4
màu khác nhau. Hỏi có bao nhiêu sự lựa chọn (về màu áo và cỡ áo)?
Câu 2. Một người có
4
cái quần khác nhau,
6
cái áo khác nhau,
3
chiếc cà vạt khác nhau. Hỏi có bao
nhiêu cách chọn một cái quần hoặc một cái áo hoặc một cái cà vạt?
Câu 3. Trên bàn có
8
cây bút chì khác nhau,
6
cây bút bi khác nhau và
10
cuốn tập khác nhau. Một học
sinh muốn chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một cuốn
tập thì số cách chọn khác nhau bằng bao nhiêu?
Câu 4. Trong một trường THPT, khối
11
có
280
học sinh nam và
325
học sinh nữ. Nhà trường cần chọn
một học sinh ở khối
11
đi dự dạ hội của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách
chọn?
HỆ THỐNG BÀI TẬP TỰ LUẬN.
II
=
PHƯƠNG PHÁP.
1
=
BÀI TẬP.
2
=

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
DẠNG 2: QUY TẮC NHÂN
Nếu một công việc nào đó phải hoàn thành qua n giai đoạn liên tiếp, trong đó:
Giai đoạn 1 có m
1
cách thực hiện
Giai đoạn 2 có m
2
cách thực hiện
…. ……….
Giai đoạn n có m
n
cách thực hiện
Khi đó, có:
12
. ...
n
m m m
cách để hoàn thành công việc đ cho.
Ta thường gặp các bài toán sau:
Bài toán 1: Đếm số phương án liên quan đến số tự nhiên
Khi lập một số tự nhiên
1
...
n
x a a=
ta cần lưu ý:
*
0,1,2,...,9
i
a
và
1
0a
.
*
x
là số chẵn
n
a
là số chẵn
*
x
là số lẻ
n
a
là số lẻ
*
x
chia hết cho
12
3 ...
n
a a a + + +
chia hết cho
3
*
x
chia hết cho
4
1nn
aa
−
chia hết cho
4
*
x
chia hết cho
5 0,5
n
a
*
x
chia hết cho 6
x
là số chẵn và chia hết cho
3
*
x
chia hết cho
21
8
n n n
a a a
−−
chia hết cho
8
*
x
chia hết cho
12
9 ...
n
a a a + + +
chia hết cho
9
.
*
x
chia hết cho
11
tổng các chữ số ở hàng lẻ trừ đi tổng các chữ số ở hàng chẵn là một số
nguyên chia hết cho
11
.
*
x
chia hết cho
25
hai chữ số tận cùng là
00,25,50,75
.
Bài toán 2: Đếm số phương án liên quan đến kiến thức thực tế
Bài toán 3: Đếm số phương án liên quan đến hình học
PHƯƠNG PHÁP.
1
=

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 1. Từ thành phố
A
đến thành phố B có 3 con đường, từ thành phố B đến thành phố C có 4 con đường.
Có bao nhiêu cách đi từ thành phố A đến thành phố C, biết phải đi qua thành phố
Câu 2. Từ các số 0,1,2,3,4,5 có thể lập được bao nhiêu số tự nhiên mà mỗi số có 6 chữ số khác nhau và
chữ số 2 đứng cạnh chữ số 3?
Câu 3. Có 3 học sinh nữ và 2 hs nam.Ta muốn sắp xếp vào một bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu
cách sắp xếp để:
1. 3 học sinh nữ ngồi kề nhau
2. 2. 2 học sinh nam ngồi kề nhau.
Câu 4. Xếp 6 người A, B, C, D, E, F vào một ghế dài.Hỏi có bao nhiêu cách sắp xếp sao cho:
1. A và F ngồi ở hai đầu ghế
2. A và F ngồi cạnh nhau
3. A và F không ngồi cạnh nhau
Câu 5. Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số
0,1,2,4,5,6,8
Câu 6. Từ các số
1,2,3,4,5,6
có thể lập được bao nhiêu số tự nhiên,mỗi số có 6 chữ số đồng thời thỏa
điều kiện:sáu số của mỗi số là khác nhau và trong mỗi số đó tổng của 3 chữ số đầu nhỏ hơn
tổng của 3 số sau một đơn vị
Câu 7. Bạn An có 3 cái áo và 4 cái quần. Hỏi bạn An có mấy cách chọn
a) Một cái quần hoặc một cái áo? b) Một bộ quần áo ?
Câu 8. Cho hai đường thẳng song song
,’dd
. Trên
d
lấy
10
điểm phân biệt, trên
’d
lấy
15
điểm phân
biệt. Hỏi có bao nhiêu tam giác mà đỉnh của nó được chọn từ
25
đỉnh nói trên?
BÀI TẬP.
2
=