Chương I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Chủ đề 1: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG A. PHƯƠNG PHÁP
+ Trong một tam giác vuông, bình phương mỗi cạnh
góc vuông bằng tích của cạnh huyền với hình chiếu
của cạnh góc vuông đó lên cạnh huyền. 2 2
b = ab , c = ac
+ Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu
của hai cạnh góc vuông trên cạnh huyền Công thức: 2
h = b c
+ Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền với đường cao tương ứng
Công thức: ah = bc
+ Trong một tam giác vuông, nghịch đảo bình phương đường cao bằng tổng các nghịch đảo bình
phương hai cạnh góc vuông Công thức: 1 1 1 = + 2 2 2 h b c
B. BÀI TẬP MẪU CÓ HƯỚNG DẪN GIẢI
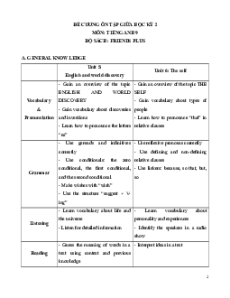
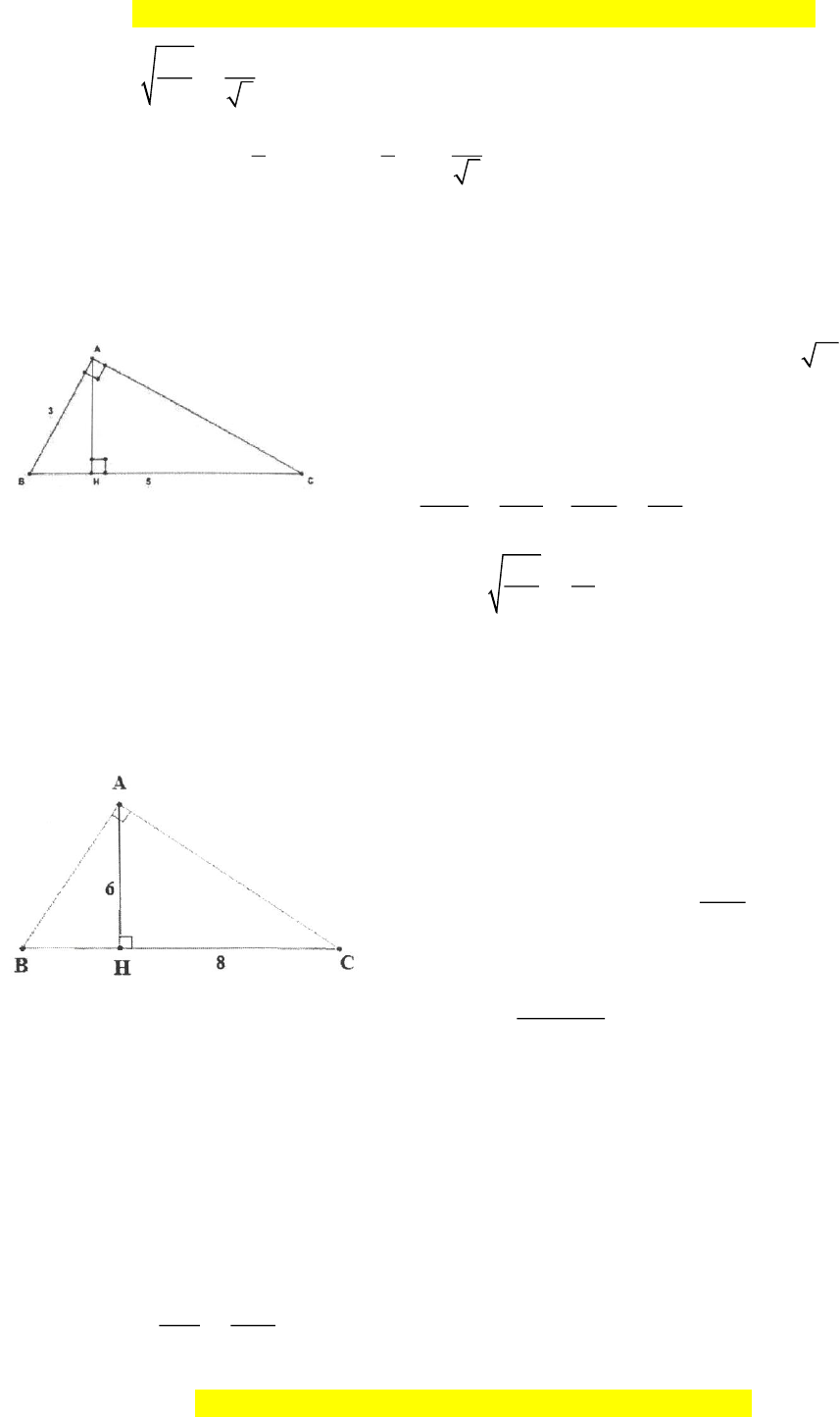
Bài tập mẫu 1: Cho ABC
vuông tại A , đường cao AH . Biết: BH = 9cm , CH = 16cm
a. Tính độ dài các cạnh A , B AC
b. Tính chiều cao AH. Hướng dẫn giải
a. Ta có: BC = BH + HC = 9 + 16 = 25(cm) ABC
vuông ở A, AH ⊥ BC (gt).
Sử dụng hệ thức về góc vuông và hình chiếu của nó lên cạnh huyền ta có: 2
AB = BH BC = 9 25 = 225
AB = 225 = 15(cm) 2 = = = AC CH CB 16 25 400
Suy ra: AC = 400 = 20 (cm)
Chú ý: Khi tính AB (hoặc AC ) ta có thể sử dụng Pitago để tính cạnh còn lại.
b. Theo hệ thức liên hệ giữa đường cao thuộc cạnh huyền và hai hình chiếu của hai góc vuông trên cạnh huyền Ta có: 2
AH = BH HC = 9 16 = 144. Suy ra: AH = 144 = 12 (cm ) Cách khác: Trong ABH vuông, theo Pythagore Ta có : 2 2 2 2 2
AH = AB − BH = 15 − 9 = 225 − 81 = 144. Nên: AH = 144 = 12 (cm) .
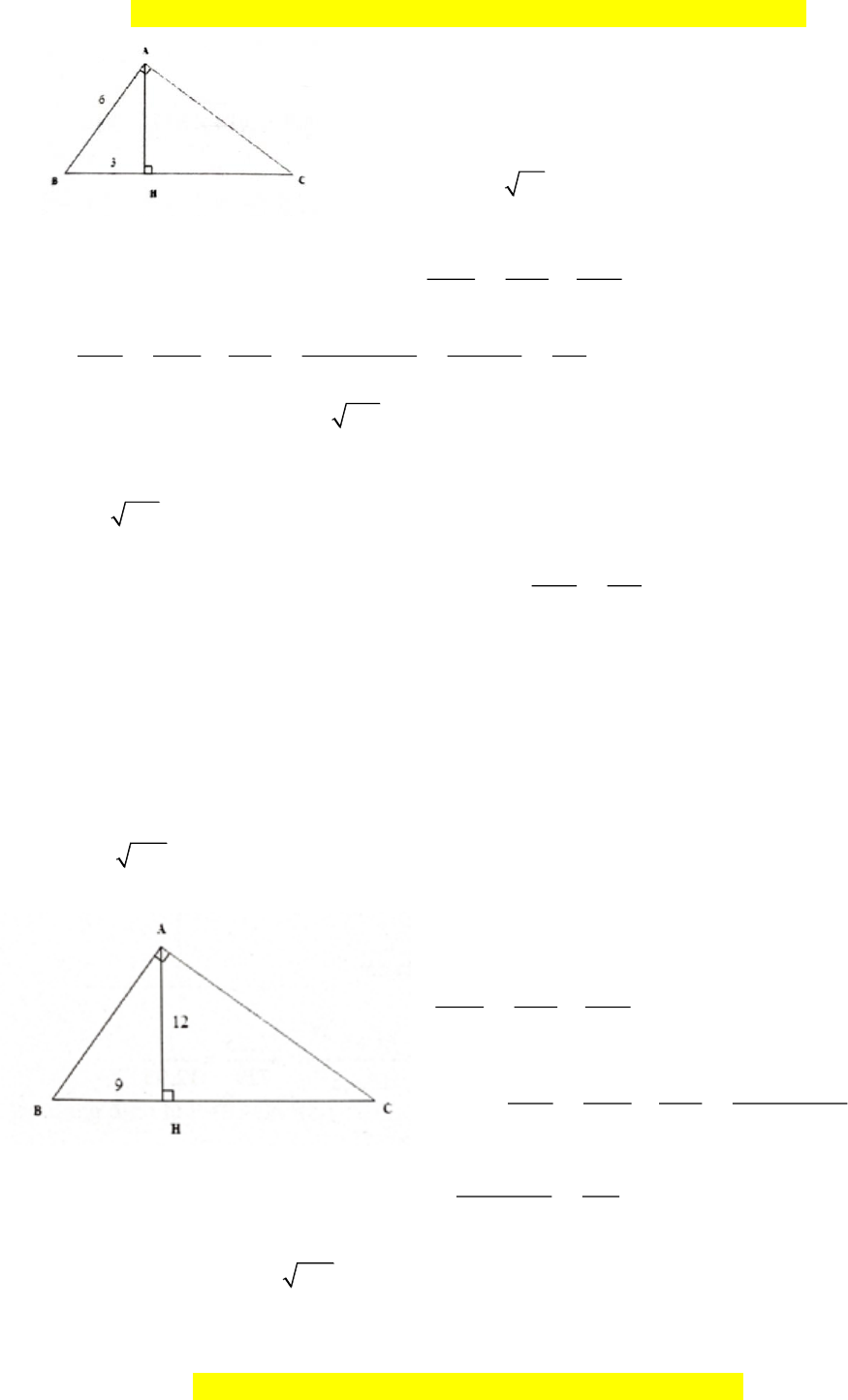
Bài tập mẫu 2: Cho ABC vuông tại ,
A ,đường cao AH .
a. Biết AH = 6c ,
m BH = 4,5cm . Tính A ,
B AC, BC, HC .
b. Biết AB = 6c ,
m BH = 3cm . Tính AH , AC,CH . Hướng dẫn giải
a. Áp dụng định lý Pythagore cho A
HB vuông tại H có: 2 2 2 2 2
AB = AH + BH = 6 + 4,5 = 56,25 Suy ra: AB = 56, 25 = 7, 5(cm)
Áp dụng hệ thức lượng trong ABC vuông tại ,
A AH là chiều cao ta được: 1 1 1 = + 2 2 2 AH AB AC 2 2 2 2 1 1 1 AB − AH 7,5 − 6 20, 25 1 Suy ra: = − = = = = 2 2 2 2 2 2 2 AC AH AB AB AH 7,5 6 2025 100 Vậy: 2
AC = 100 . Hay: AC = 100 = 10 (cm)
Theo định lý Pythagore ta có: 2 2 2 2 2
BC = AB + AC = 7,5 + 10 = 156, 25 Suy ra: BC = 156, 25 = 12, 5(cm) 2 2 Theo hệ thức: AC 10 2 AC = H .
C BC . Suy ra : HC = = = 8(cm) BC 12,5
b. ABH vuông tại H có: 2 2 2
AB = AH + BH 2 2 2 2 2
AH = AB − BH = 6 − 3 = 27
Vậy: AH = 27 5, 2(cm) 1 1 1 ABC vuông tại ,
A AH là đường cao ta có: = + 2 2 2 AH AB AC 2 2 1 1 1 AB − AH 36 − 27 1 Suy ra: = − = = = 2 2 2 2 2 AC AH AB AB AH 27.37 108 Do đó: 2
AC = 108 . Suy ra: AC = 108 = 10, 39 (cm) Mặt khác: 2 2 2
BC = AB + AC = 36 + 108 = 144 .
Vậy BC = 144 = 12(cm) 2
Áp dụng hệ thức lượng ta có: AC 108 2
AC = BC.CH CH = = = 9(cm) . BC 12
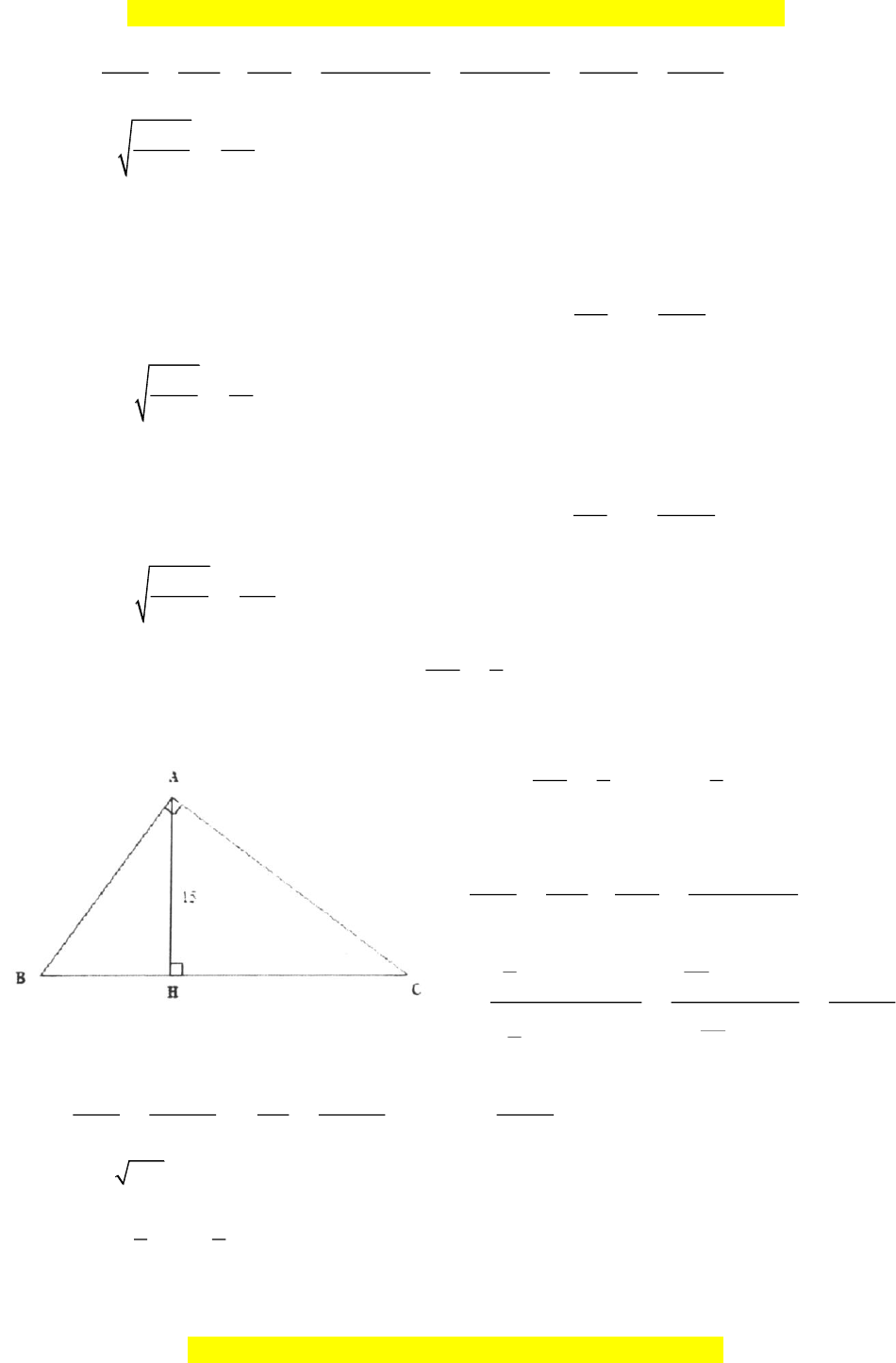
Bài tập mẫu 3: Cho ABC
vuông tại A , đường cao AH , tính diện tích ABC , biết AH = 12c , m BH = 9cm Hướng dẫn giải
Áp dụng định lý Pythagore trong A
HB ,vuông tại H Ta có: 2 2 2 2 2
AB = AH + BH = 9 + 12 = 225
Vậy: AB = 225 = 15(cm) ABC vuông tại ,
A AH là đường cao ta có: 1 1 1 = + 2 2 2 AH AB AC 2 2 1 1 1 AB − AH Suy ra: = − = 2 2 2 2 2 AC AH AB AB AH 225 − 144 1 = = 225 144 400 Do đó: 2
AC = 400 AC = 400 = 20 (cm) + ABC vuông tại ,
A AB và AC là hai cạnh góc vuông của tam giác
1 1 Nên: S = AB AC = 15 20 = 150( 2 cm ) . 2 2
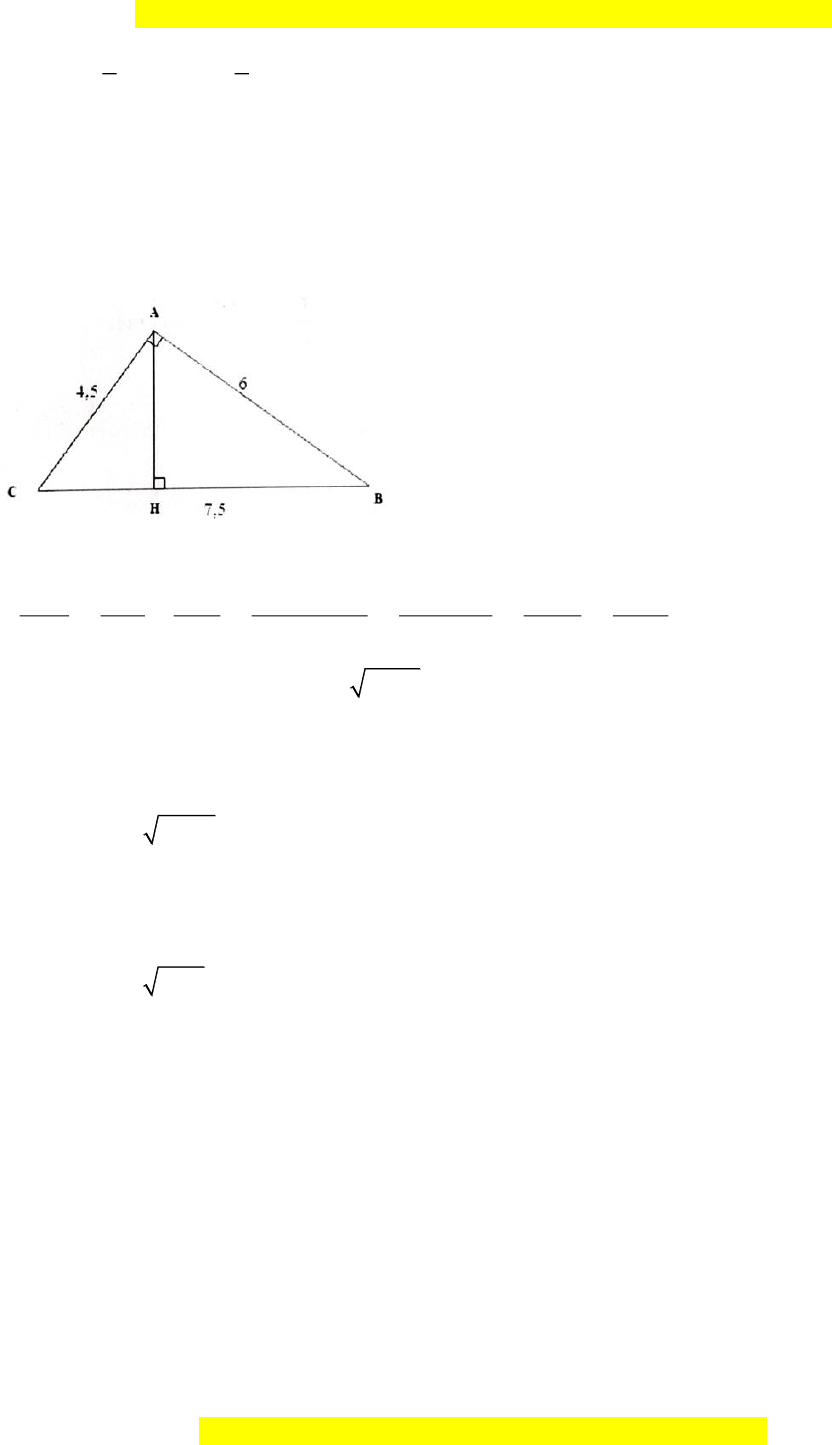
Bài tập mẫu 4: Cho ABC
, biết BC = 7,5c , m CA = 4,5c , m AB = 6cm a. ABC
là tam giác gì? Tính đường cao AH của ABC ;
b. Tính độ dài các đoạn thẳng BH,CH. Hướng dẫn giải a. ABC là tam giác vuông. Thật vậy: 2 2 2 7,5 = 4,5 + 6 5625 = 5625 Thỏa mãn hệ thức 2 2 2
BC = AB + AC Do đó: ABC vuông tại A Trong ABC vuông tại ,
A AH là đường cao ta có: 2 2 2 2 1 1 1 AB + AC 6 + 4,5 56, 25 1 = + = = = = 2 2 2 2 2 2 2 AH AB AC AB AC 6 4,5 729 12,96 Vậy: 2 AH
= 12,96 . Suy ra: AH = 12,96 = 3,6(cm) .
b. Áp dụng định lý Pythagore cho A
HB vuông tại H ta được: 2 2 2 2 2 2 2 2
AB = AH + BH BH
= AB − AH = 6 − 3,6 = 23,04
Do đó: BH = 23,04 = 4,8(cm)
Áp dụng định lý Pythagore cho AHC vuông tại H ta được: 2 2 2
AC = AH + HC Nên: 2 2 2 2 2
HC = AC − AH = 4,5 − 3,6 = 7, 29
Do đó: HC = 7, 29 = 2,7 (cm)
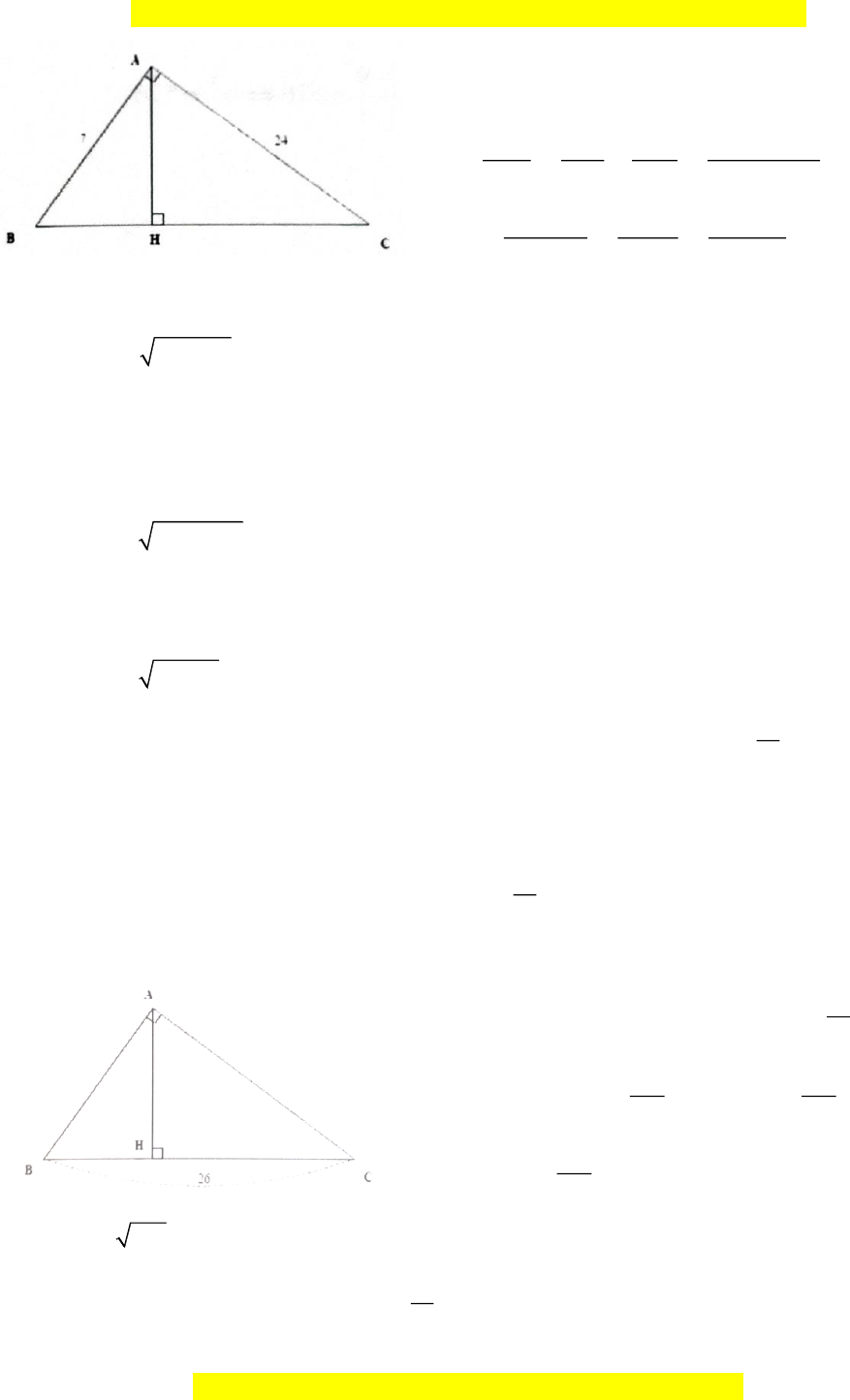
Bài tập mẫu 5: Cho tam giác vuông với các cạnh góc vuông lần lượt là 7 và 24 . Kẻ đường cao ứng
với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền. Hướng dẫn giải
Không mất tính tổng quát gọi các cạnh của tam giác vuông có độ dài lần lượt như hình vẽ.
(Chuyên đề) Phương pháp giải Toán 9 Hình học (cơ bản, nâng cao)
0.9 K
468 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ Chuyên đề Phương pháp giải Toán 9 Hình học từ cơ bản đến nâng cao gồm các dạng bài tập với phương pháp giải chi tiết nhằm giúp Giáo viên có thêm tài liệu tham khảo.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(936 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 9
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Chương I: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Chủ đề 1: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
A. PHƯƠNG PHÁP
+ Trong một tam giác vuông, bình phương mỗi cạnh
góc vuông bằng tích của cạnh huyền với hình chiếu
của cạnh góc vuông đó lên cạnh huyền.
22
,b ab c ac=
=
+ Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu
của hai cạnh góc vuông trên cạnh huyền
Công thức:
2
h b c=
+ Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền với đường cao
tương ứng
Công thức:
ah bc=
+ Trong một tam giác vuông, nghịch đảo bình phương đường cao bằng tổng các nghịch đảo bình
phương hai cạnh góc vuông
Công thức:
2 2 2
1 1 1
h b c
=+
B. BÀI TẬP MẪU CÓ HƯỚNG DẪN GIẢI
Bài tập mẫu 1: Cho
ABC
vuông tại
A
, đường cao
AH
. Biết:
9BH cm=
,
16CH cm=
a. Tính độ dài các cạnh
,AB AC
b. Tính chiều cao
.AH
Hướng dẫn giải
a. Ta có:
( )
9 16 25 cmBC BH HC= + = + =
ABC
vuông ở
A, AH BC⊥
(gt).
Sử dụng hệ thức về góc vuông và hình chiếu của nó lên cạnh huyền ta có:
2
9 25 225AB BH BC= = =
( )
225 15 cmAB = =
2
16 25 400AC CH CB= = =

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Suy ra:
( )
400 20AC cm==
Chú ý: Khi tính
AB
(hoặc
AC
) ta có thể sử dụng Pitago để tính cạnh còn lại.
b. Theo hệ thức liên hệ giữa đường cao thuộc cạnh huyền và hai hình chiếu của hai góc vuông trên
cạnh huyền
Ta có:
2
9 16 144.AH BH HC= = =
Suy ra:
( )
144 12 AH cm==
Cách khác: Trong
ABH
vuông, theo Pythagore
Ta có :
2 2 2 2 2
15 9 225 81 144.AH AB BH= − = − = − =
Nên:
( )
144 12AH cm==
.
Bài tập mẫu 2: Cho
ABC
vuông tại
,A
,đường cao
.AH
a. Biết
6 , 4,5AH cm BH cm==
. Tính
, , ,AB AC BC HC
.
b. Biết
6 , 3AB cm BH cm==
. Tính
,,AH AC CH
.
Hướng dẫn giải
a. Áp dụng định lý Pythagore cho
AHB
vuông tại
H
có:
2 2 2 2 2
6 4,5 56,25AB AH BH= + = + =
Suy ra:
( )
56,25 7,5AB cm==
Áp dụng hệ thức lượng trong
ABC
vuông tại
,A AH
là chiều cao ta được:
2 2 2
1 1 1
AH AB AC
=+
Suy ra:
2 2 2 2
2 2 2 2 2 2 2
1 1 1 7,5 6 20,25 1
7,5 6 2025 100
AB AH
AC AH AB AB AH
−−
= − = = = =
Vậy:
2
100AC =
. Hay:
( )
100 10AC cm==
Theo định lý Pythagore ta có:
2 2 2 2 2
7,5 10 156,25BC AB AC= + = + =
Suy ra:
( )
156,25 12,5BC cm==
Theo hệ thức:
2
.AC HC BC=
. Suy ra :
( )
22
10
8
12,5
AC
HC cm
BC
= = =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
b.
ABH
vuông tại
H
có:
2 2 2
AB AH BH=+
2 2 2 2 2
6 3 27AH AB BH = − = − =
Vậy:
( )
27 5,2AH cm=
ABC
vuông tại
,A AH
là đường cao ta có:
2 2 2
1 1 1
AH AB AC
=+
Suy ra:
22
2 2 2 2 2
1 1 1 36 27 1
27.37 108
AB AH
AC AH AB AB AH
−−
= − = = =
Do đó:
2
108AC =
. Suy ra:
( )
108 10,39AC cm==
Mặt khác:
2 2 2
36 108 144BC AB AC= + = + =
.
Vậy
( )
144 12BC cm==
Áp dụng hệ thức lượng ta có:
( )
2
2
108
.9
12
AC
AC BC CH CH cm
BC
= = = =
.
Bài tập mẫu 3: Cho
ABC
vuông tại
A
, đường cao
AH
, tính diện tích
ABC
, biết
12 , 9AH cm BH cm==
Hướng dẫn giải
Áp dụng định lý Pythagore trong
AHB
,vuông tại
H
Ta có:
2 2 2 2 2
9 12 225AB AH BH= + = + =
Vậy:
( )
225 15AB cm==
ABC
vuông tại
,A AH
là đường cao ta có:
2 2 2
1 1 1
AH AB AC
=+
Suy ra:
22
2 2 2 2 2
1 1 1 AB AH
AC AH AB AB AH
−
= − =
225 144 1
225 144 400
−
==
Do đó:
( )
2
400 400 20AC AC cm= = =
+
ABC
vuông tại
,A AB
và
AC
là hai cạnh góc vuông của tam giác
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Nên:
( )
2
11
15 20 150
22
S AB AC cm= = =
.
Bài tập mẫu 4: Cho
ABC
, biết
7,5 , 4,5 , 6BC cm CA cm AB cm= = =
a.
ABC
là tam giác gì? Tính đường cao
AH
của
;ABC
b. Tính độ dài các đoạn thẳng
,.BH CH
Hướng dẫn giải
a.
ABC
là tam giác vuông.
Thật vậy:
2 2 2
7,5 4,5 6 5625 5625= + =
Thỏa mãn hệ thức
2 2 2
BC AB AC=+
Do đó:
ABC
vuông tại
A
Trong
ABC
vuông tại
,A AH
là đường cao ta có:
2 2 2 2
2 2 2 2 2 2 2
1 1 1 6 4,5 56,25 1
6 4,5 729 12,96
AB AC
AH AB AC AB AC
++
= + = = = =
Vậy:
2
12,96AH =
. Suy ra:
( )
12,96 3,6AH cm==
.
b. Áp dụng định lý Pythagore cho
AHB
vuông tại
H
ta được:
2 2 2 2 2 2 2 2
6 3,6 23,04AB AH BH BH AB AH= + = − = − =
Do đó:
( )
23,04 4,8BH cm==
Áp dụng định lý Pythagore cho
AHC
vuông tại
H
ta được:
2 2 2
AC AH HC=+
Nên:
2 2 2 2 2
4,5 3,6 7,29HC AC AH= − = − =
Do đó:
( )
7,29 2,7HC cm==
Bài tập mẫu 5: Cho tam giác vuông với các cạnh góc vuông lần lượt là 7 và 24 . Kẻ đường cao ứng
với cạnh huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền.
Hướng dẫn giải
Không mất tính tổng quát gọi các cạnh của tam giác vuông có độ dài lần lượt như hình vẽ.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Áp dụng hệ thức lượng trong
ABC
vuông tại
,B AH
là đường cao. Ta được:
22
2 2 2 2 2
1 1 1 AB AC
AH AB AC AB AC
+
= + =
22
22
7 24 625 1
7 24 28224 45,1584
+
= = =
Vậy :
2
45,1584AH =
Do đó:
45,1584 6,72AH ==
Đường cao
AH
chia cạnh huyền
BC
thành các đoạn
,.HB HC
Áp dụng định lý Pythagore trong
AHC
vuông tại
H
Ta có:
2 2 2 2 2 2 2 2
24 6,72 530,8416AC AH HC HC AC AH= + = − = − =
Do đó:
530,8416 23,04.HC ==
Áp dụng định lý Pythagore trong
AHB
vuông tại
H
Ta có:
2 2 2 2 2 2 2 2
7 6,72 3,8416AB AH BH BH AB AH= + = − = − =
Do đó:
( )
3,8416 1,96 .BH cm==
Bài tập mẫu 6: Cho một tam giác vuông, biết tỉ số hai cạnh góc vuông là
5
12
, cạnh huyền là
26 cm
. Tính độ dài các cạnh góc vuông và hình chiếu của cạnh góc vuông trên cạnh huyền.
Hướng dẫn giải
Gọi độ dài của
( )
AB x cm=
, khi đó độ dài của
( )
5
12
AC x cm=
Do:
ABC
là tam giác vuông tại
A
nên áp dụng định lý Pythagore ta được:
2
2 2 2 2 2
5
26
12
BC AB AC x x
= + = +
2 2 2
25 25
676 1 676
144 144
x x x
= + + =
22
169
676 576
144
xx = =
Do đó:
( )
576 24x cm==
Vậy độ dài của
AB
là
( )
24 cm
và
AC
là :
( )
5
24 10 .
12
cm=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta lại có :
2 2 2 2
2 2 2 2 2 2 2
1 1 1 24 10 676 169
24 10 57600 14400
AB AC
AH AB AC AB AC
++
= + = = = =
Nên:
( )
14400 120
169 13
AH cm==
Đường cao
AH
chia cạnh huyền
BC
thành các đoạn
,.HB HC
Áp dụng định lý Pythagore trong
AHC
vuông tại
H
ta có:
2
2 2 2 2 2 2 2
120 2500
10
13 169
AC AH HC HC AC AH
= + = − = − =
Do đó:
( )
2500 50
3,85 cm
169 13
HC = =
Áp dụng định lý Pythagore trong
AHB
vuông tại
H
ta có:
2
2 2 2 2 2 2 2
120 82944
24
13 169
AB AH BH BH AB AH
= + = − = − =
Do đó:
( )
82944 288
22,15 .
169 13
BH cm= =
Bài tập mẫu 7: Cho
ABC
vuông ở
A
. Biết
5
,
7
AB
AC
=
đường cao
15 .AH cm=
Tính HB, HC.
Hướng dẫn giải
Ta có:
55
.
77
AB
AB AC
AC
= =
Áp dụng hệ thức lượng trong tam giác vuông có
22
2 2 2 2 2
1 1 1 AB AC
AH AB AC AB AC
+
= + =
2
22
2
2
4
2
5 25
1
74
7 49
25
25
5
49
7
AC AC AC
AC
AC
AC AC
++
= = =
Do đó:
2
2
2 2 2 2
1 74 1 74 15 .74
666
25 15 25 25
AC
AH AC AC
= = = =
Vậy:
( )
666 25,81AC cm=
Suy ra:
( )
55
25,81 18,44
77
AB AC cm= = =
Đường cao
AH
chia cạnh huyền
BC
thành các đoạn
,.HB HC

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Áp dụng định lý Pythagore trong
AHC
vuông tại
H
Ta có:
2 2 2 2 2 2
666 225 441AC AH HC HC AC AH= + = − = − =
Suy ra:
( )
441 21HC cm==
Áp dụng định lý Pythagore trong
AHB
vuông tại
H
Ta có:
2 2 2 2 2 2 2 2
18,44 15 115,0336AB AH BH BH AB AH= + = − = − =
Do đó:
( )
115,0336 10,73BH cm=
Bài tập mẫu 8: Cho hình thang cân
( )
//ABCD AB CD
, biết
26 ,AB cm=
10AD cm=
và đường
chéo
AC BC⊥
. Tính diện tích của hình thang
ABCD
.
Hướng dẫn giải
Gọi các đỉnh của hình thang cân như hình vẽ.
Hạ chiều cao
CH
của hình thang cân
ABCD
.
Do
ABCD
là hình thang cân nên:
( )
10AD CB cm==
Mặt khác:
ACB
vuông tại
C
(gt)
Do đó: Áp dụng định lý Pythagore trong
ACB
ta có:
2 2 2 2 2 2 2 2
26 10 576AB AC BC AC AB BC= + = − = − =
Vì vậy:
( )
576 24AC cm==
Áp dụng hệ thức lượng trong
ACB
vuông, với
CH
là đường cao ta được:
2 2 2 2
2 2 2 2 2 2 2
1 1 1 24 10 676
24 10 57600
AC CB
CH CB AC AC CB
++
= + = = =
Do đó:
( )
57600
9,23
676
CH cm=
Lại có:
( )
22
2
10
3,85
26
cm
CB
CB HB AB HB
AB
= = = =
Mặt khác:
( )
2 26 2.3,85 18,3DC AB HB cm= − = − =
Nên diện tích hình thang cân
ABCD
là:
( )
2
18,3 26
9,23 204,44
22
DC AB
S CH cm
++
=
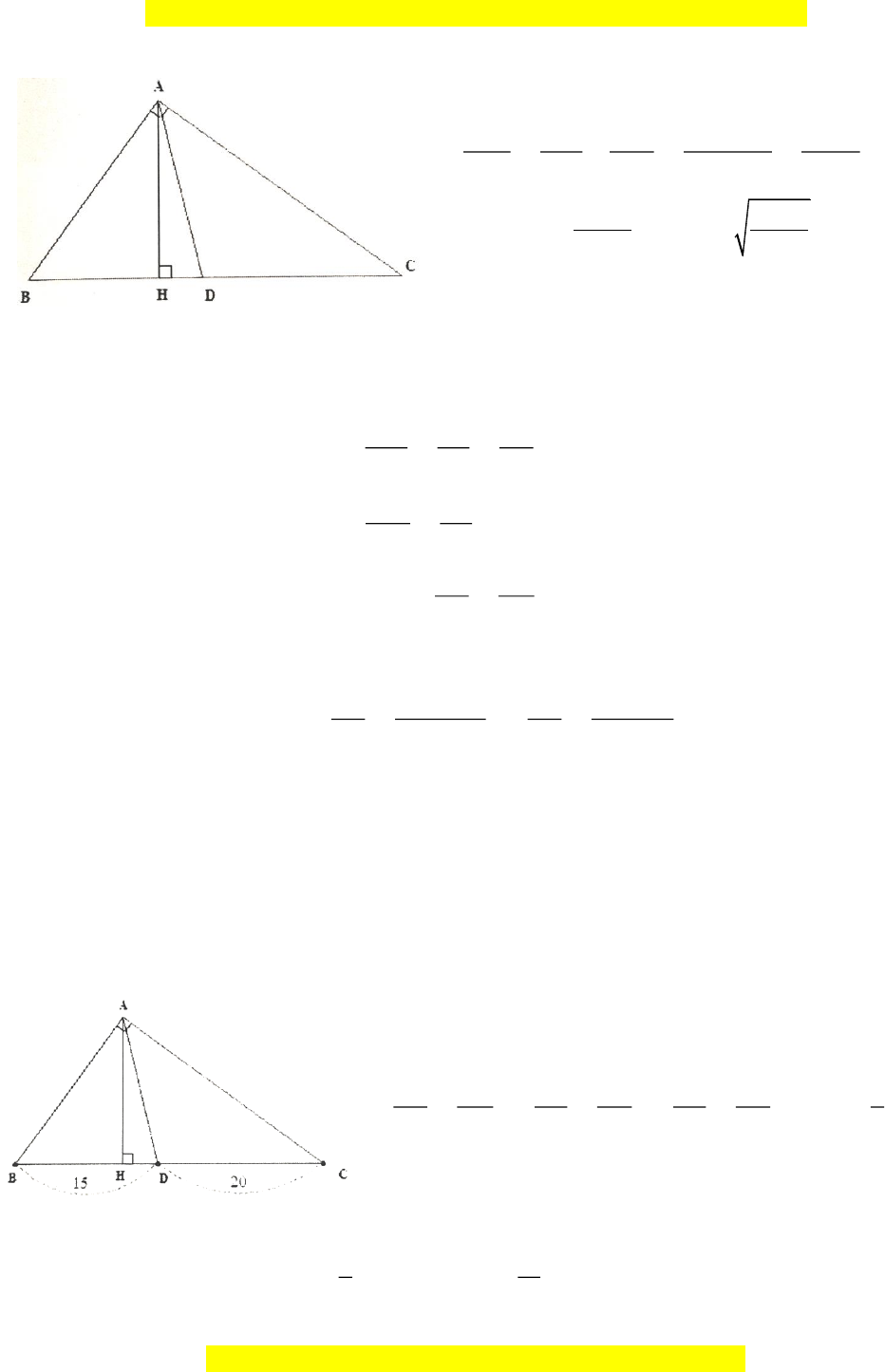
Bài tập mẫu 9: Cho
ABC
vuông ở
A, 12 , 16AB cm AC cm==
, phân giác
AD
, đường cao
AH
.
Tính độ dài
,,HB HD HC
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Hướng dẫn giải
Áp dụng hệ thức lượng trong tam giác vuông ta có :
22
2 2 2 2 2
1 1 1 12 16 400
12 16 36864AH AB AC
+
= + = =
Vậy:
( )
2
36864 36864
9,6
400 400
AH AH cm= = =
Áp dụng định lý Pythagore trong
ABC
ta được:
2 2 2 2 2
12 16 400BC AB AC= + = + =
.
Do đó:
( )
20BC cm=
.
Ta lại có:
( )
22
2
12 144
7,2
20 20
AB
AB BH BC BH cm
BC
= = = = =
Ngoài ra:
( )
22
2
16
12,8
20
AC
AC HC BC HC cm
BC
= = = =
Theo tính chất của đường phân giác ta được:
( )
1
DB DC
AB AC
=
Mà:
( )
2DC BC BD=−
Thay (2) vào (1) ta được hệ thức:
20
12 16
DB BC BD DB BD
AB AC
−−
= =
( ) ( )
16 20 12 16 240 12 28 240 8,57BD BD BD BD BD BD cm = − = − =
Nhìn vào hình vẽ ta được:
( )
8,57 7,2 1,37HD BD BH cm= − −
.
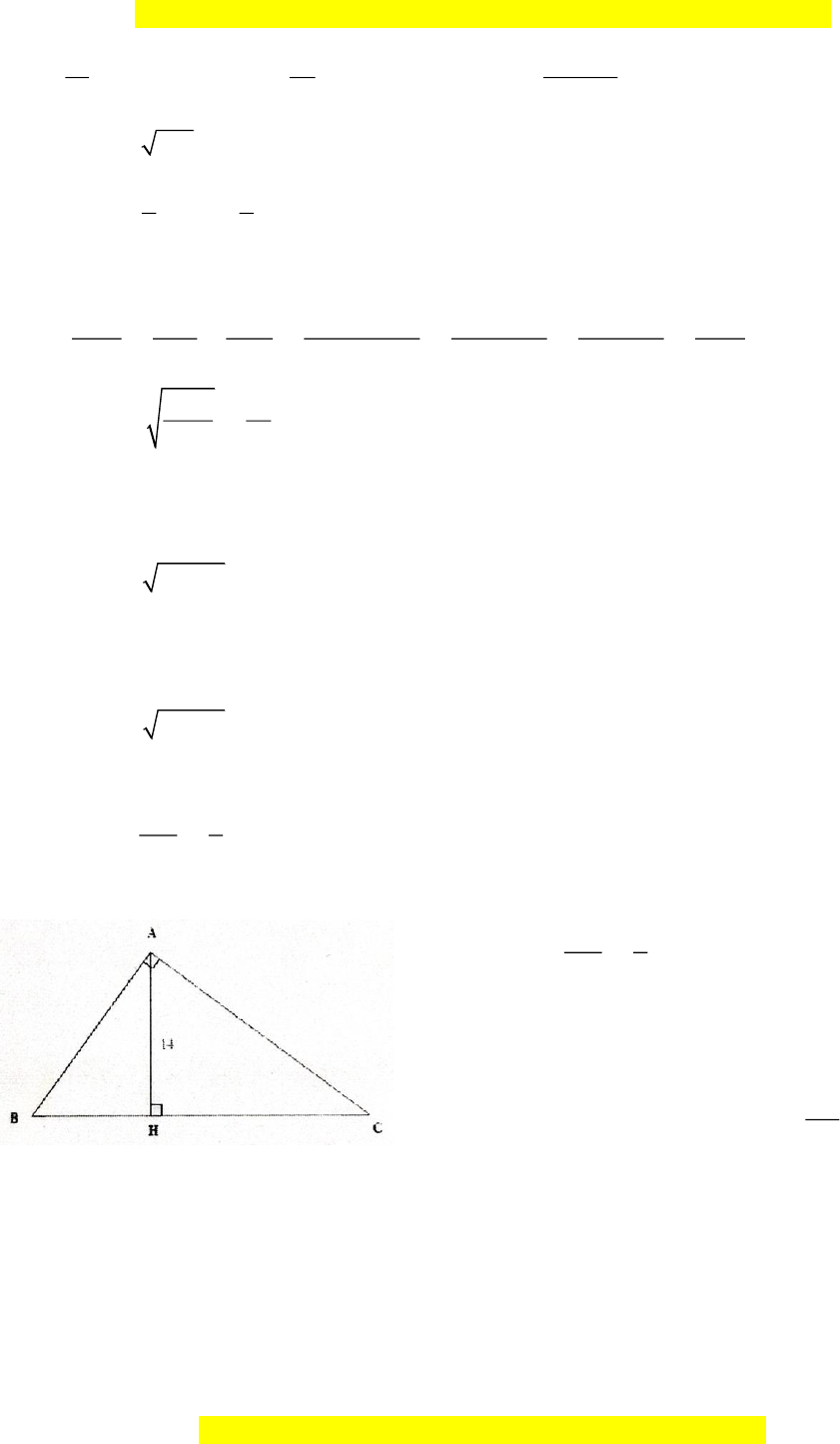
Bài tập mẫu 10: Cho
ABC
vuông ở
A
, phân giác
AD
đường cao
AH
. Biết
15 , 20BD cm CD cm==
. Tính độ dài các đoạn thẳng
,.BH HC
Hướng dẫn giải
Ta có:
( )
15 20 35BC BD DC cm= + = + =
Áp dụng tính chất đường phân giác ta có tỉ lệ thức:
( )
15 20 3 4 3
1
4
DB DC
AB AC
AB AC AB AC AB AC
= = = =
Áp dụng định lý Pythagore cho
ABC
vuông tại
A
ta được:
( )
2 2 2
2BC AB AC=+
Thay (1) vào (2) ta được:
2
2 2 2 2 2
39
4 16
BC AC AC AC AC BC
= + + =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
2
2 2 2 2 2
9 25 35 16
1 35 35 784
16 16 25
AC AC AC
+ = = = =
Do đó:
( )
784 28AC cm==
Suy ra:
( )
33
28 21
44
AB AC cm= = =
Áp dụng hệ thức lượng trong
ABC
vuông tại
,A
đường cao
AH
Ta có:
2 2 2 2
2 2 2 2 2 2 2
1 1 1 21 28 1225 25
21 28 3345744 7056
AB AC
AH AB AC AB AC
++
= + = = = =
Suy ra:
( )
7056 84
16,8
25 5
AH cm= = =
Áp dụng định lý Pythagore trong
CAH
vuông tại
H
ta có:
2 2 2 2 2 2 2 2
28 16,8 501,76AC AH HC HC AC AH= + = − = − =
Do đó:
( )
501,76 22,4 cmHC ==
.
Áp dụng định lý Pythagore trong
AHB
vuông tại
H
ta có:
2 2 2 2 2 2 2 2
21 16,8 158,76AB AH BH BH AB AH= + = − = − =
Do đó:
( )
158,76 12,6 cmBH ==
.
Bài tập mẫu 11: Cho
ABC
vuông ở
A
, đường cao
AH
, tính chu vi của tam giác
ABC
. Biết
1
14 cm,
4
HB
AH
HC
==
.
Hướng dẫn giải
Ta có:
1
4
4
HB
HC HB
HC
= =
Áp dụng hệ thức lượng trong
ABC
ta có:
2
AH HB HC=
2
22
14
14 4 49
4
HB HB HB = = =
Vậy
( )
7 cmHB =
và
( )
28 cmHC =
Suy ra:
( )
28 7 35 cmBC = + =
Áp dụng Pythagore trong
AHB
vuông tại
H
.
Ta có:
2 2 2 2 2
14 7 245AB AH HB= + = + =
. Vậy:
( )
15,65 cmAB
Áp dụng định lý Pythagore trong
AHC
vuông tại
H
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có:
2 2 2 2 2
14 28 980AC AH HC= + = + =
. Vậy:
( )
31,3 cmAC =
Do đó: Chu vi
ABC
là:
( )
31,3 15,65 35 81,95 cmC AB BC AC= + + = + + =
.
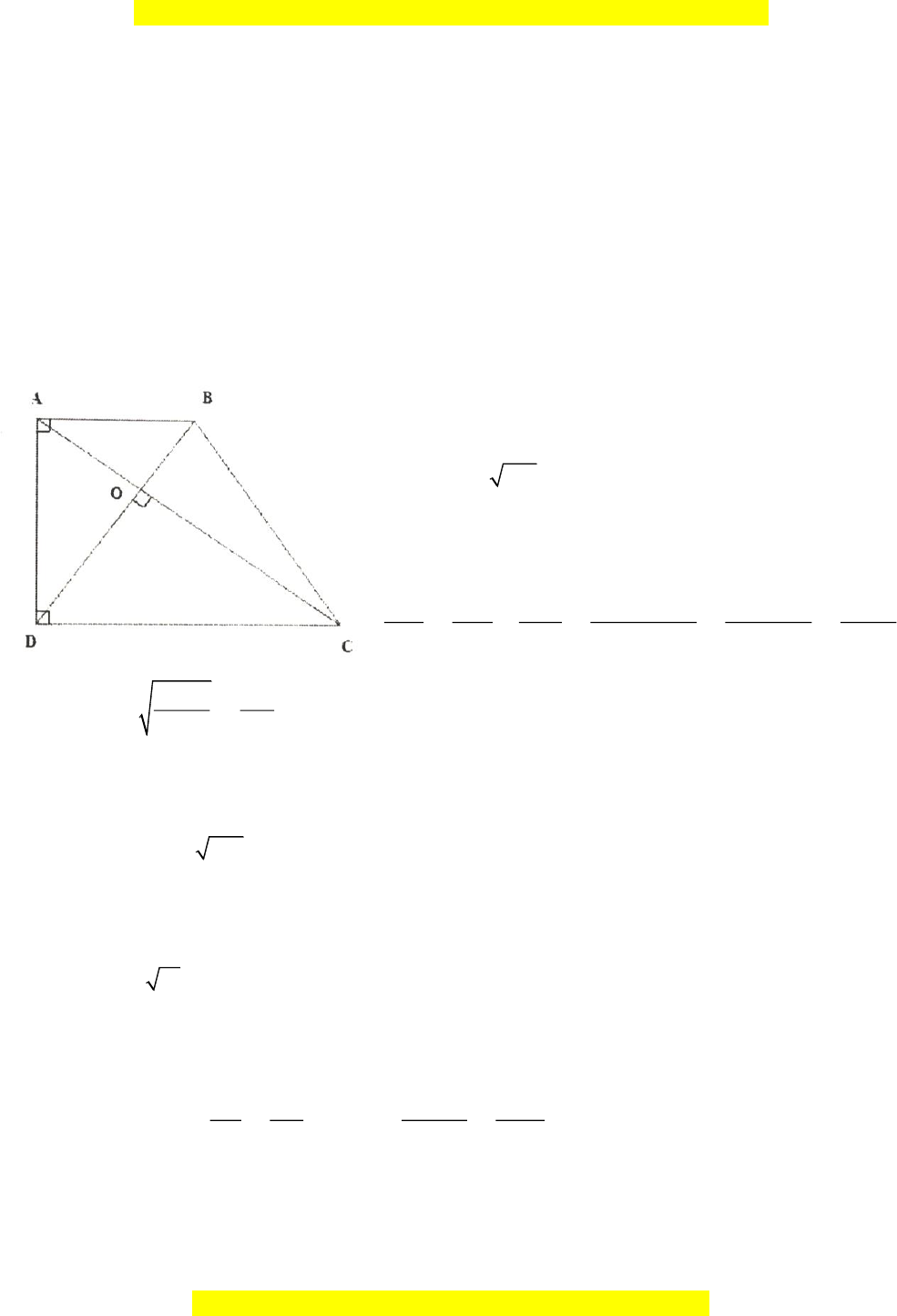
Bài tập mẫu 12: Cho hình thang vuông
, 90ABCD A D= =
,
15 cm, 20 cmAB AD==
. Các
đường chéo
AC
và
BD
vuông góc với nhau ở
O
a. Tính độ dài
,OB OD
b. Tính độ dài đường chéo
AC
c. Tính diện tích hình thang
ABCD
Hướng dẫn giải
a. Áp dụng Pythagore cho
DAB
vuông tại
A
Ta có:
2 2 2 2 2
15 20 625BD AB AD= + = + =
Vậy:
( )
625 25 cmBD ==
.
Trong
DAB
vuông tại
,A AO
là đường cao của
ABD
.
Nên:
2 2 2 2
2 2 2 2 2 2 2
1 1 1 15 20 625
15 20 90000
AB AD
OA AB AD AB AD
++
= + = = =
Suy ra:
( )
90000 300
12 cm
625 25
OA = = =
Áp dụng định lý Pythagore cho
AOD
vuông tại
O
. có :
2 2 2 2 2 2 2 2
20 12 256AD AO OD OD AD AO= + = − = − =
Từ đây ta có:
( )
256 16 cmOD ==
Áp dụng định lý Pythagore cho
AOB
vuông tại
O
, ta có:
2 2 2 2 2 2 2 2
15 12 81AB AO OB OB AB AO= + = − = − =
Từ đây:
( )
81 9OB cm==
b. Ta có:
AC AO OC=+
Do
ABCD
là hình thang nên:
ΔOBA ODC∽
Từ đó ta có tỉ lệ thức:
( )
. 12.16
21,33
9
OB OD OAOD
OC cm
OA OC OB
= = = =
Vậy:
( )
12 21,33 33,33AC OA OC cm= + + =
c. Áp dụng định lý Pythagore cho
ΔODC
vuông tại
O
ta có:
2 2 2 2 2
16 21,33 277,33DC OD OC= + = + =

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Suy ra:
( )
277,33 16,65DC cm=
Do đó:
( ) ( )
( )
2
11
20 15 16,65 316,5
22
ABCD
S AD AB DC cm= + + =
.
Bài tập mẫu 13: Cho hình chữ nhật
ABCD
. Đường phân giác trong của
B
cát đường chéo
AC
thành hai đoạn lân lượt có độ dài là
2
4
7
m
và
5
5
7
m
. Tính các kích thước của hình chữ nhật.
Hướng dẫn giải
Trong
ΔABC
, gọi
BE
là đường phân giác của
B
.
Theo tính chất của đường phân giác ta có:
( )
1
AE CE AE AB
AB CB CE CB
= =
Thay vào:
2
4
3
7
5
4
5
7
AE AB AB AB
CE CB CB CB
= = =
Bình phương hai vế ta được:
2
2
9
16
AB
CB
=
Áp dụng định lý Pythagore cho
ΔABC
vuông tại
B
ta có:
2 2 2
AC AB BC=+
Xét tỉ số:
2 2 2 2
2 2 2
9 16 5 5
16 4 4
AC AB BC AC
CB CB CB
++
= = = =
Mặt khác:
25
4 5 10
77
AC AE EC= + = + =
. Thay vào:
8BC =
Suy ra:
3 3.8
6
44
BC
AB = = =
Vậy các kích thước của hình chữ nhật là
6m
và
8m
.
Bài tập mẫu 14: Cho
ΔABC
vuông tại
A
, vẽ đường cao
AH
. Chu vi của
ΔABH
là
30cm
và chu
vi của
ΔACH
là
40cm
. Tính chu vi của
ΔABC
.
Hướng dẫn giải
Gọi
1 2 3
;;P P P
lần lượt là chu vi của
Δ ,ΔAHB CHA
và
ΔCAB
.
Dễ thẫy:
ΔAHB CHA∽
. Nên:
1
2
P
AB
P CA
=
Do đó ta có :
3
4 3 4
AB AB AC
CA
= =
. Nên:
2 2 2 2 2
2 2 2 2 2
3 4 3 4 5
AB AC AB AC BC+
= = =
+

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Từ đây ta có các tỉ lệ tương ứng :
3 4 5
AB AC BC
==
Mặt khác :
ΔAHB CHA CAB∽∽
Từ đó ta cũng có được:
1 2 3
: : : : 3 : 4 : 5P P P AB AC BC==
Do đó: Chu vi
ΔABH
là
30cm
và chu vi
ΔACH
là
40cm
thì chu vi
ΔABC
là
50cm
.
Bài tập mẫu 15: Cho
ΔABC
vuông tại
A
có cạnh
6AB cm=
và
8AC cm=
. Các đường phân
giác trong và ngoài của góc
B
cắt đường thẳng
AC
lần lượt là
M
và
N
. Tính
AM
và
AN
.
Hướng dẫn giải
Áp dụng định lý Pythagore cho
ΔABC
vuông tại
A
ta được:
( )
2 2 2 2 2
6 8 100 10 cmBC AB AC BC= + = + = =
Theo tính chất của đường phân giác ta có hệ thức:
AM CM AM AB
AB CB CM CB
= =
Suy ra:
6
3
8 16
AM AB AM
AM
AM CM AB CB
= = =
++
Trong
ΔBMN
do
,BM BN
lần lượt là đường phân giác trong và phân giác ngoài của góc
B
của
ΔABC
Do đó:
BM BN⊥
. Vì vậy:
ΔBMN
vuông tại
B
.
Trong đó:
AB
là đường cao ứng với cạnh huyền
MN
Ta có:
( )
2
12BA AM AN AN cm= =
. Suy ra:
( )
( )
3
2
AM cm
AN cm
=
=
.
Bài tập mẫu 16: Cho
ΔABC
. Từ một điểm
M
bất kì trong tam giác kẻ
MD
,
MF
lần lượt vuông
góc với các cạnh
,,BC CA AB
.
2 2 2 2 2 2
CMR : BD CE AF DC EA FB+ + = + +
Hướng dẫn giải
Ta có biến đổi:
2 2 2
VT BD CE AF= + +
( ) ( ) ( )
2 2 2 2 2 2
BM DM CM ME AM MF= − + − + −
(Do
Δ ,Δ , ΔBMD CME AMF
vuông tại
,,D E F
)
2 2 2 2 2 2
BM DM CM ME AM MF= − + − + −
2 2 2 2 2 2
CM DM AM ME BM MF= − + − + −
( ) ( ) ( )
2 2 2 2 2 2
CM DM AM ME BM MF= − + − + −

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
2 2 2
DC EA FB VP= + + =
(Do các
Δ ,Δ , ΔCMD AME BMF
vuông tại
, , )D E F
(đpcm).
Bài tập mẫu 17: Cho
ΔABC
vuông tại
A
, đường cao
AH
, biết
4AB cm=
,
7,5AC cm=
. Tính
,HB HC
.
Hướng dẫn giải
Áp dụng định lý Pythagore cho
ΔABC
vuông tại
A
ta được:
2 2 2 2 2
4 7,5 72,25BC AB AC= + = + =
Do đó:
( )
72,25 8,5BC cm==
Áp dụng hệ thức lượng trong
ΔABC
có:
2
AB BC BH=
Suy ra:
( )
22
4 16
1,88
8,5 8,5
AB
BH cm
BC
= = =
.
Tương tự:
2
.AC BC HC=
Nên
( )
22
7,5 56,25
6,62
8,5 8,5
AC
HC cm
BC
= = = =
Bài tập mẫu 18: Cho
ΔABC
vuông tại
A
cạnh
( )
10AB cm=
, đường cao
( )
5AH cm=
. Tỉnh các
góc và diện tích của
ΔABC
.
Hướng dẫn giải
Trong
ΔAHB
vuông tại
H
Nên:
51
sin
10 2
AH
ABH
AB
= = =
Suy ra:
30ABH =
Ta có:
( )
180 180 180 90 30 60A B C C A B+ + = = − + = − − =
Áp dụng hệ thức lượng trong tam giác vuông với
AH
là đường cao
Ta có:
2 2 2 2 2 2
1 1 1 1 1 1
AH AB AC AC AH AB
= + = −
2 2 2 2
2 2 2 2 2
1 10 5 3
10 5 100
AB AH
AC AH AB
−−
= = =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Suy ra:
( )
100 10
3
3
AC cm==
Diện tích
ΔABC
là :
( )
2
1 1 10
10 28,87
22
3
S AB AC cm= =
.
Bài tập mẫu 19: Cho
ΔABC
vuông tại
A
, có
( ) ( )
3 , 5AB cm BC cm==
,
AH
là chiều cao của
ΔABC
. Tính độ dài của
AC
và
AH
của
ΔABC
.
Hướng dẫn giải
Ta có:
2 2 2
16AC BC AB= − =
. Do đó:
( )
16 4AC cm==
Áp dụng hệ thức lượng trong
ΔABC
vuông tại
A
, đường cao
AH
ta có:
2 2 2
1 1 1 25
144AH AB AC
= + =
Suy ra:
( )
144 12
25 5
AH cm==
Bài tập mẫu 20: Cho
ΔABC
vuông tại
,A AH
là đường cao
( )
H BC
có
6;AH cm=
8.HC cm=
Tính độ dài
,AC BC
và
AB
Hướng dẫn giải
Ta có:
2 2 2
AC AH HC=+
Suy ra:
( )
2
100 10AC AC cm= =
Mà:
( )
2
2
. 12,5
AC
AC BC HC BC cm
HC
= = =
Mặt khác:
AB AC AH BC =
.
Nên:
( )
7,5
AH BC
AB cm
AC
==
C. BÀI TẬP LUYỆN TẬP CÓ ĐÁP ÁN HOẶC HƯỚNG DẪN GIẢI
Bài tập 1: Cho
ΔABC
vuông tại
, 30 , 6A C BC cm= =
, đường cao
AH
. Tính
;;AB AC AH
.
Bài tập 2: Cho
ΔABC
vuông tại
A
có đường cao
AH
. Gọi
,MN
lần lượt là chân đường vuông
góc kẻ từ
H
đến
,AB AC
. Cho biết:
9 , 16BH cm HC cm==
.
a. Tính độ dài các cạnh
,,BC AB AC
và
AH
.
b. Chứng minh:
3
3
CN AC
BM AB
=
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài tập 3: Cho
ΔABC
vuông tại
A
có đường cao
AH
.
1. Cho biết
3 ; 4AB cm AC cm==
. Tính độ dài các đoạn
, , ,BC HB HC AH
.
2. Vẽ
HE AB⊥
tại
,E HF AC⊥
tại
F
.
a. CMR:
2
AE EB EH=
; b.
2
CMR : AE EB AF FC AH + =
.
3. Chứng minh:
3
cosBE BC B=
.
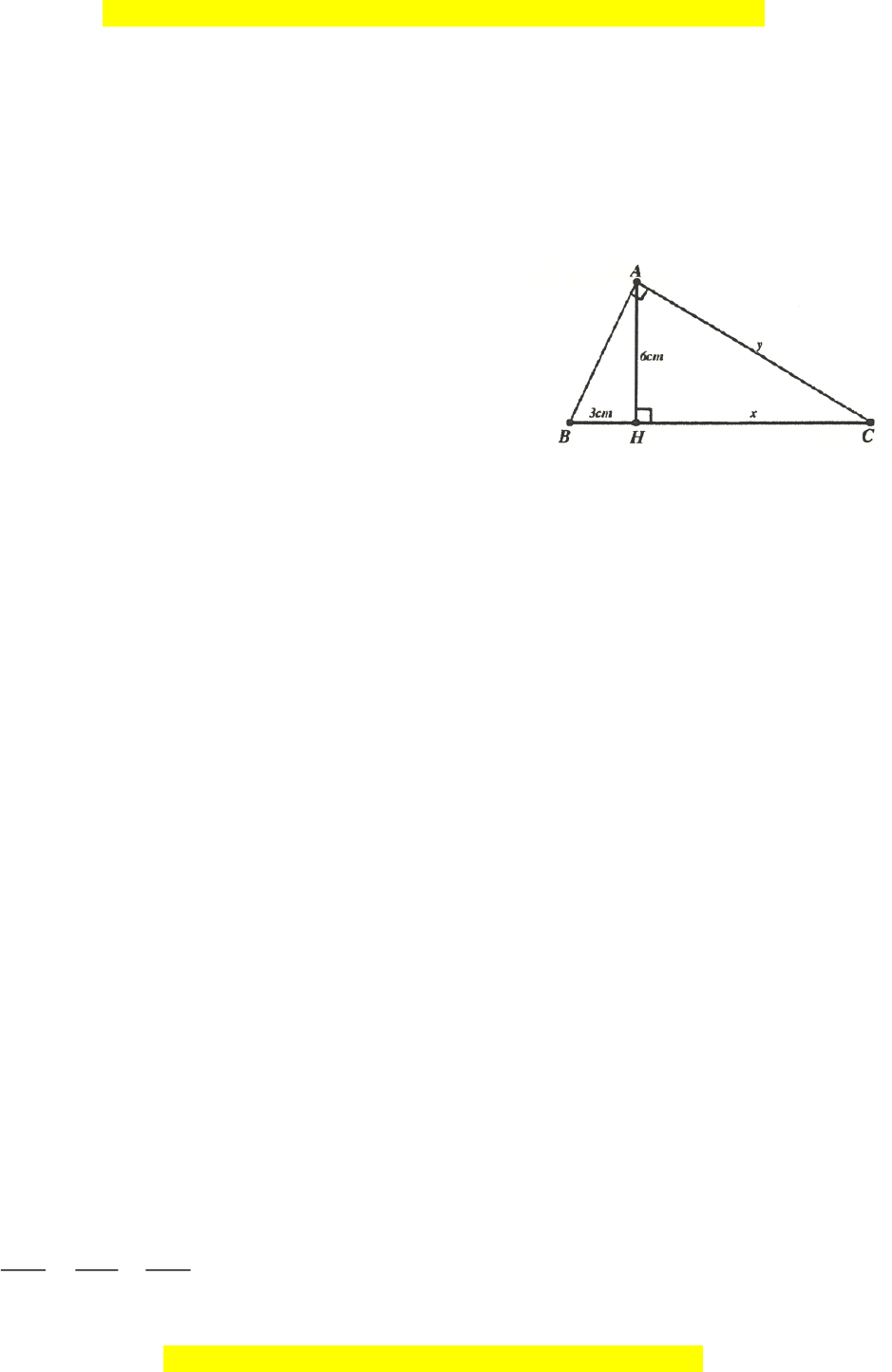
Bài tập 4: Tìm
;xy
trong hình vẽ bên:
Bài tập 5: Cho
ΔABC
vuông tại
A
, đường cao
AH
, biết
8 ; 2BC cm BH cm==
.
a. Tính độ dài
,AB AC
và
AH
.
b. Trên cạnh
AC
lã
y điểm
( )
;K K A K C
. Gọi
D
là hình chiếu của
A
trên
BK
.
Chứng minh:
BD BK BH BC =
Bài tập 6: Cho
ΔABC
có cạnh
12 , 16 , 20AB cm AC cm BC cm= = =
. Kẻ đường cao
AM
. Kẻ
ME AB⊥
.
a. CMR:
ΔABC
vuông. b. Tính độ dài
,AM BM
.
c. CMR:
22
AE AB AC MC = −
. d. CMR:
AE AB MB MC EM AC = =
Bài tập 7: Cho đường tròn tâm
O
đường kính
13AB cm=
. Dây
CD
có độ dài
12cm
vuông góc
với
OA
tại
H
a. Tính
;HC OH
.
b. Gọi
,MN
theo thứ tự là hình chiếu của
H
trên
,AC BC
. Chứng minh:
CM CA CN CB =
c. Tính diện tích tứ giác
CMHN
.
Bài tập 8: Cho hình vuông
ABCD
. Trên cạnh
BC
lấy điểm
E
, tia
AE
cắt đường thẳng
CD
tại
.G
Trên nửa mặt phẳng bờ là đường thẳng
AE
chứa tia
AD
kẻ đoạn thẳng
AF
sao cho
AF AE⊥
và
AF AE=
. Chứng minh:
a.
FD BE=
b. Các điểm
,,F D C
thẳng hàng.
c.
2 2 2
1 1 1
AD AE AG
=+
Bài tập 9: Cho
ΔABC
vuông tại
A
, đường cao
AH
, biết
9 ; 15AB cm BC cm==
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a. Tính
AH
và
CH
.
b. Qua
B
kẻ đường thẳng vuông góc với
BC
cắt
AC
tại
D
. Phân giác
C
cắt
AB
tại
N
và
BD
tại
M
. Chứng minh:
CN CD CM CB =
.
Bài tập 10: Cho
ΔABC
vuông tại
A
, đường cao
, 3 , 6AH AB cm BC cm==
. Gọi
,EF
lần lượt là
hình chiếu của
H
trên cạnh
AB
và
AC
.
a. Giải tam giác vuông
ABC
b. Tính độ dài
AH
và chứng minh:
EF AH=
.
c. Tính:
EA EB AF FC +
Bài tập 11: Cho hình vuông
ABCD
. Qua điểm
A
vẽ một đường thẳng cắt cạnh
BC
tại
E
và cắt
đường thẳng
CD
tại
F
.
2 2 2
1 1 1
:CM
AB AE AF
=+
D. HƯỚNG DẪN GIẢI HOẶC ĐÁP ÁN
Bài tập 1:
+ Trong
ΔABC
vuông tại
A
.
Nên:
( )
sin 6sin30 3 cmAB BC C= = =
( )
3
cot : tan 3 : 3 3 cm
3
AC AB C AB C= = = =
+ Trong
ΔAHC
vuông tại
H
, nên:
( )
33
sin 3 3 sin30 cm
2
AH AC C= = =
Bài tập 2:
a. Ta có:
( )
9 16 25 cmBC BH HC= + = + =
.
⦁
( )
9 16 12 cmAH BH CH= = =
⦁
( )
9.25 15 cmAB BH BC= = =
⦁
( )
16 25 20 cmAC HC BC= = =
b. Ta có:
( )
12 16
9,6 cm
20
AH HC
HN AM
AC
= = = =
Do đó:
( )
15 9,6 5,4 cmBM AB AM AM HN= − = − = − =
Tương tự:
( )
12,8 cmCN =
. Do đó:
( )
12,8 64
1
5,4 27
CN
BM
==
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta lại có:
( )
33
33
20 64
2
15 27
AC
AB
==
Từ (1) và (2) suy ra:
3
3
64
27
CN AC
BM AB
==
(đccm).
Bài tập 3:
1. Áp dụng định lí Pythagore với
ΔABC
tại A ta có:
( )
2 2 2 2
3 4 25 5 cmBC AB AC= + = + = =
Trong
ΔABC
vuông ta có:
22
2
3
1,8cm
5
AB
AB BC HB HB
BC
= = = =
Nên:
5 1,8 3,2HC BC HB cm= − = − =
.
+ Ta có:
AH BC AB AC =
. Suy ra:
34
2,4cm
5
AB AC
AH
BC
= = =
2. Trong
ΔAHB
vuông tại
H
có
HE
là đường cao nên:
2
AE AB AH=
Trong
ΔAHC
vuông tại
H
có
HF
là đường cao nên:
2
AF AC AH=
Do đó:
( ) ( )
AE EB AF FC AE AB AE AF AC AF + = − + −
( )
2 2 2 2 2 2
AE AB AE AF AC AF AH AH AE AF= − + − = + − +
Tứ giác
AEHF
có:
90AEH AFH EAF= = =
Nên: tứ giác
AEHF
là hình chữ nhật. Do đó:
EF AH=
Và
( )
2 2 2 2
2AE AF EF AH+==
Từ (1) và (2) suy ra:
2 2 2
. . 2 (AE EB AF FC AH AH AH+ = − =
đpcm)
Cách khác:
Trong
ΔAHB
vuông tại
H
có
HE
là đường cao nên:
2
AE EB EH=
Trong
ΔAHC
vuông tại
H
có
HF
là đường cao nên:
2
AF FC FH=
Chứng minh tứ giác
AEHF
là hình chữ nhật. Suy ra:
AH EF=
Mà:
2 2 2
EH FH EF+=
. Suy ra đpcm.
Bài tập 4:
2
6
12cm; 12.15 6 5cm
3
xy= = = =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài tập 5:
a. Ta có:
ΔABC
vuông tại
A
, đường cao
AH
:
2
2.8 16 4 cmAB BH BC AB= = = =
2 2 2
BC AB AC=+
(định lý Pythagore)
Nên:
2 2 2 2
8 4 4 3cmAC BC AB= − = − =
Ta cũng có:
8 2 6cmHC BC HB= − = − =
Và
2
. 2.6 12cmAH BH CH= = =
.
Suy ra:
12 2 3cmAH ==
b. Trong
ΔABK
vuông tại
A
, đường cao
2
AD AB BD BK =
(1)
Mà:
( )
2
cmtAB BH BC=
(2)
Từ (1), (2) suy ra:
BD BK BH BC =
Bài tập 6:
a.
ABC
vuông (theo Pythagore đảo).
b. Ta có:
AM BC AB AC =
.
Nên:
( )
9,6 cmAM =
Ta có:
2
AB BM BC=
Thay vào:
( )
7,2 cmBM =
.
c. Ta có:
2
2 2 2
AE AB AM
AM AC MC
=
=−
.
Suy ra:
22
AE AB AC MC = −
d. Ta có:
( )
2
AE AB MB MC AM = =
Mặt khác:
ΔAEM CMA∽
. Suy ra:
2
EM AC AM=
.
Vậy:
EM AC AE AB MB MC = =
.
Bài tập 7:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a. Xét
( )
;OR
có đường kính
AB CD H⊥=
(gt)
Ta có bán kính
1
6,5cm
2
R AB==
Áp dụng định lý Pythagore trong tam giác vuông HOC, ta có:
2 2 2 2 2
6,5 6 6,25OH OC CH= − = − =
Do đó:
6,25 2,5 cmOH ==
b. Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông
,AHC CHB
ta có
( )
2
1 CM CA CH=
( )
2
2CN CB CH=
Từ (1) và (2) suy ra:
CM CA CN CB =
c. Ta có
( )
.CHN ABC g g∽
Do đó:
22
6 36
13 169
CHN
ABC
S
CH
S AB
= = =
Ta lại có:
2
1
13 6 39 cm
2
ABC
S = =
. Nên:
36 108
39
169 13
CHN
S = =
Mà tứ giác
CMHN
là hình chữ nhật
Vậy:
2
216 8
2 16 cm
13 3
CMHN CHN
SS= = =
Bài tập 8:
a.
( )
ABE ADF c g c = − −
Do đó:
BE FD=
b. Vì
( )
ABE ADF c g c = − −
Nên:
90ADF ABE= =
.
Do đó:
180ADF ADC+ =
Vì vậy:
;;F D C
thẳng hàng
c. Áp dụng hệ thức lượng trong tam giác vuông
AFG
ta có:
2 2 2
1 1 1
AD AG AF
=+
Mà
AF AE=
nên
2 2 2
1 1 1
.
AD AE AG
=+

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài tập 9:
a. Ta có:
2 2 2 2
15 9 12 cmAC BC AB= − = − =
(định lý
Pythagore)
ABC
vuông tại
A
, đường cao
AH
,
Ta có:
AH BC AB AC =
(hệ thức lượng)
Do đó:
9 12
7,2 cm
15
AB AC
AH
BC
= = =
.
Ta có:
2
AC BC CH=
(hệ thức lượng)
22
12
9,6 cm.
15
AC
CH
BC
= = =
b. Ta có:
( ) ( )
12
.
CN CA
C C gt CAN CBM g g
CM CB
= =∽
( )
1
Chứng minh được:
( )
CA CB
CAB CBD g g
CB CD
=∽
( )
2
Từ
( )( )
1 2 . .
CN CB
CN CD CM CB
CM CD
= =
Bài tập 10:
a.
ABC
vuông tại
A
, nên:
31
cos
62
AB
B
BC
= = =
.
Suy ra:
60B =
Do đó:
90 60 30C = − =
Nên:
sin 6 sin60 3 3 cmAC BC B= = =
b. Tính độ dài
AH
và chứng minh
EF AH=
AHB
vuông tại
H
nên:
33
sin 3 sin60 cm
2
AH AB B= = =
Tứ giác
AEHF
có:
( )
90 gtA AEH AFH= = =
Nên tứ giác
AEHF
là hình chữ nhật. Do đó:
EF AH=
c. Tính:
..EA EB AF FC+
Ta có:
2
2
EA EB HE
AF FC FH
=
=
. Nên
2 2 2
EA EB AF FC HE FH EF + = + =
Mà
( )
EF AH cmt=
Do đó:
2
2
3 3 27
6,75 cm
24
EA EB AF FC AH
+ = = = =
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài tập 11:
Qua
A
dựng đường thẳng vuông góc với
AF
cắt
DC
tại
M
.
Ta có: tứ giác
AECM
nội tiếp (vì
EAM ECM=
)
Nên:
45EAM ECA= =
(vì
45 )ECA =
Do đó:
AME
vuông cân tại
A
Vì vậy
AE AM=
Xét
AMF
vuông tại
A
có
AD
là đường cao nên
2 2 2
1 1 1
AD AM AF
=+
vì
AD AB
AM AE
=
=
Do đó:
2 2 2
1 1 1
AB AE AF
=+
.