Chuyên đề Toán 11 Vận dụng, Vận dụng cao (sách mới)

CHUYÊN ĐỀ 1: GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC
a) Đường tròn lượng giác
- Đường tròn lượng giác là đường tròn có tâm tại gốc toạ độ, bán
kính bằng 1 , được định hướng và lấy điểm (
A 1;0) làm điểm gốc của đường tròn.
- Điểm trên đường tròn lượng giàc biểu diễn góc lượng giác có số
đo  (độ hoặc rađian) là điểm M trên đường tròn lượng giác sao cho sđ (O , A OM ) =  .
b) Giá trị lượng giác của góc lượng giác
- Hoành độ x của điểm M được gọi là côsin của  , kí hiệu là cos . cos = . x
- Tung độ y của điểm M được gọi là sin của  , kí hiệu là sin  . sin = y cos
- Nếu sin  0 , tỉ số sin được gọi là côtang của  , kí hiệu là cot . cos x cot  = = (y  0) sin  y
- Các giá trị cos,sin, tan, cot  được gọi là
các giá trị lượng giác của  . Chú ý
a) Ta còn gọi trục tung là trục sin, trục hoành là trục côsin.
b) Từ định nghĩa ta suy ra:
* sin , cos xác định với mọi giá trị của  và ta có: 1
−  sin 1; −1 cos 1; sin( + k2 ) = sin; cos( + k2 ) = cos (k  ). 
* tan xác định khi  
+ k (k  ) . 2
* cot  xác định khi   k (k  ) .
- Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điềm biều diễn M trên đường
tròn lượng giác (H.1.10) .


c) Giá trị lượng giác của các góc đặc biệt
d) Sử dụng MTCT để đổi số đo và tìm giá trị lượng giác của góc
Tùy thuộc dòng máy tính, gv có thể hướng dẫn trực tiếp cho học sinh
2. QUAN HỆ GIỮA GIÁ TRỊ LƯỢNG GIÁC
a) Các công thức lượng giác cơ bản 2 2 sin  + cos  = 1 1    2 1+ tan  =
  + k , k    2 cos   2  1 2 1+ cot  =
(  k , k  ) 2 sin   k  tan .cot  = 1   , k  .    2 
b) Giá trị lượng giác của các góc có liên quan đặc biệt
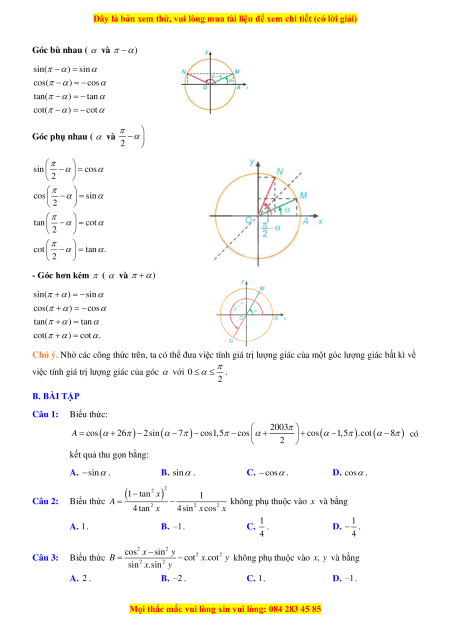
- Góc đối nhau (  và  − ) cos(  − ) = cos sin(  − ) = −sin tan(  − ) = − tan cot(  − ) = − cot


Góc bù nhau (  và  − ) sin( −  ) = sin 
cos( −  ) = − cos
tan( −  ) = − tan 
cot( −  ) = − cot  
Góc phụ nhau (  và   −  2     sin − = cos    2     cos − = sin    2     tan − = cot    2     cot − = tan.    2 
- Góc hơn kém  (  và  +  ) sin( +  ) = − sin 
cos( +  ) = − cos tan( +  ) = tan  cot( +  ) = cot .
Chú ý. Nhờ các công thức trên, ta có thể đưa việc tính giá trị lượng giác của một góc lượng giác bất kì về 
việc tính giá trị lượng giác của góc  với 0    . 2 B. BÀI TẬP Câu 1: Biểu thức:    A = ( +  )− ( −  ) 2003 cos 26 2 sin 7 − cos1,5 − cos  + + cos  
( −1,5 ).cot( −8 ) có  2  kết quả thu gọn bằng: A. −sin . B. sin . C. − cos . D. cos . (1−tan x)2 2 1 Câu 2: Biểu thức A = −
không phụ thuộc vào x và bằng 2 2 2 4 tan x 4 sin x cos x 1 1 A. 1. B. –1. C. . D. − . 4 4 2 2 cos x − sin y Câu 3: Biểu thức 2 2 B = − cot .
x cot y không phụ thuộc vào x, y và bằng 2 2 sin . x sin y A. 2 . B. –2 . C. 1. D. –1.

2 Câu 4: Biểu thức C = ( 4 4 2 2 x + x + x x) ( 8 8 2 sin cos sin cos
– sin x + cos x) có giá trị không đổi và bằng A. 2 . B. –2 . C. 1. D. –1. 1 Câu 5:
Nếu sin x + cos x =
thì 3sin x + 2cos x bằng 2 5 − 7 5 + 7 5 − 5 5 + 5 A. hay . B. hay . 4 4 7 4 2 − 3 2 + 3 3 − 2 3 + 2 C. hay . D. hay . 5 5 5 5 2b Câu 6: Biết tan x =
. Giá trị của biểu thức 2 2
A = a cos x + 2b sin .
x cos x + c sin x bằng a − c A. –a . B. a . C. –b . D. b .     9  Câu 7:
Với mọi , biểu thức: A = cos + cos  + +...+ cos  +     nhận giá trị bằng:  5   5  A. –10 . B. 10 . C. 0 . D. 5 . 0 2sin 2550 .cos ( 0 1 − 88 1 ) Câu 8:
Giá trị của biểu thức A = + bằng: 0 0 0 tan 368 2 cos 638 + cos 98 A. 1. B. 2 . C. −1. D. 0 .    Câu 9: Cho cot  = 3
− 2 với     . Khi đó giá trị tan + cot bằng: 2 2 2 A. 2 19 . B. −2 19 . C. − 19 . D. 19 . 1 1
Câu 10: Cho hai góc nhọn a và b với sin a = ,sin b =
. Giá trị của sin 2(a + b) là: 3 2 2 2 + 7 3 3 2 + 7 3 4 2 + 7 3 5 2 + 7 3 A. . B. . C. . D. . 18 18 18 18    − tan = 4 tan tan Câu 11: Nếu 2 2 thì 2 bằng: 3sin 3sin 3cos 3cos A. 5− . B. 3cos 5 + . C. 3cos 5 − . D. 3cos 5 + . 3cos 2 2cos 2 + 3 sin 4 −1
Câu 12: Biểu thức A =
có kết quả rút gọn là: 2 2sin 2 + 3 sin 4 −1 cos( 0 4 + 30 ) cos( 0 4 − 30 ) sin ( 0 4 + 30 ) sin ( 0 4 − 30 ) A. B. C. D. cos( 0 4 − 30 ) cos( 0 4 + 30 ) sin ( 0 4 − 30 ) sin ( 0 4 + 30 ) . . . .      
Câu 13: Biểu thức A = 2 2 2 cos x + cos + x + cos − x   
 không phụ thuộc x . và bằng:  3   3  3 4 3 2 A. . B. . C. . D. . 4 3 2 3