ĐỀ THI HỌC SINH GIỎI TOÁN 6 ĐỀ SỐ 9
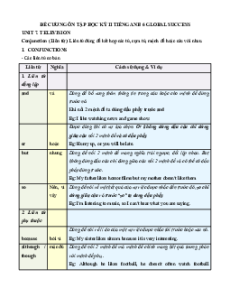
Đề Thi học sinh giỏi cấp huyện Bài 1(1,5đ): Tìm x a) 5x = 125; b) 32x = 81 ; c) 52x-3 – 2.52 = 52.3 Bài 2 (1,5đ)
Cho a là số nguyên. Chứng minh rằng:
Bài 3 (1,5đ) Cho a là một số nguyên. Chứng minh rằng:
a) Nếu a dương thì số liền sau a cũng dương.
b) Nếu a âm thì số liền trước a cũng âm.
c) Có thể kết luận gì về số liền trước của một số dương và số liền sau của một số âm? Bài 4 (2đ)
Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng
tổng của 31 số đó là số dương. Bài 5 (2đ).
Cho các số tự nhiên từ 1 đến 11 được viết theo thứ tự tuỳ ý sau đó đem cộng mỗi số
với số chỉ thứ tự của nó ta được một tổng. Chứng minh rằng trong các tổng nhận được,
bao giờ cũng tìm ra hai tổng mà hiệu của chúng là một số chia hết cho 10. Bài 6 (1,5đ):
Cho tia Ox. Trên hai nữa mặt phẳng đối nhău có bờ là Ox. Vẽ hai tia Oy và Oz sao
cho góc xOy và xOz bắng 1200. Chứng minh rằng: a)
b) Tia đối của mỗi tia Ox, Oy, Oz là phân giác của góc hợp bởi hai tia còn lại.
ĐÁP ÁN Bài 1 (1,5đ)
a) 5x = 125 5x = 53 => x= 3
b) 32x = 81 => 32x = 34 => 2x = 4 => x = 2 c) 52x-3 – 2.52 = 52.3 52x: 53 = 52.3 + 2.52 52x: 53 = 52.5 52x = 52.5.53
52x = 56 => 2x = 6 => x=3
Bài 2. Vì là một số tự nhiên với mọi a Z nên từ < 5 ta => = {0,1,2,3,4}.
Nghĩa là a ={0,1,-1,2,-2,3,-3,4,-4}. Biểu diễn trên trục số cácc số này đều lớn hơn -
5 và nhỏ hơn 5 do đó -5Bài 3.
a) Nếu a dương thì số liền sau cũng dương.
Ta có: Nếu a dương thì a>0 số liền sau a lớn hơn a nên cũng lớn hơn 0 nên là số dương
b) Nếu a âm thì số liền trước a cũng âm.
Ta có: Nếu a âm thì a<0 số liền trước a nhỏ hơn a nên cũng nhỏ hơn 0 nên là số âm. Bài 4 (2đ).
Trong các số đã cho ít nhất có 1 số dương vì nếu trái lại tất cả đều là số âm thì tổng
của 5 số bất kỳ trong chúng sẽ là số âm trái với giả thiết.
Tách riêng số dương đó còn 30 số chi làm 6 nhóm. Theo đề bài tổng các số của mỗi
nhóm đều là số dương nên tổng của 6 nhóm đều là số dương và do đó tổng của 31 số đã cho đều là số dương. Bài 5 (2đ):
Đề chọn HSG môn Toán 6 năm 2022 - 2023 có đáp án ( Đề 9 )
575
288 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Bộ 14 đề HSG Toán 6 của các trường Trung học Cơ sở, các Phòng Giáo dục và Đào tạo, các Sở Giáo dục và Đào tạo trên toàn quốc, có đáp án và lời giải chi tiết. Hỗ trợ học sinh lớp 6 trong quá trình ôn tập chuẩn bị cho kỳ thi chọn học sinh giỏi Toán 6 các cấp: cấp trường / cấp huyện / cấp tỉnh / cấp Quốc gia.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(575 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 6
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
ĐỀ THI HỌC SINH GIỎI TOÁN 6
ĐỀ SỐ 9
Đề Thi học sinh giỏi cấp huyện
Bài 1(1,5đ): Tìm x
a) 5
x
= 125;
b) 3
2x
= 81 ;
c) 5
2x-3
– 2.5
2
= 5
2
.3
Bài 2 (1,5đ)
Cho a là số nguyên. Chứng minh rằng:
Bài 3 (1,5đ) Cho a là một số nguyên. Chứng minh rằng:
a) Nếu a dương thì số liền sau a cũng dương.
b) Nếu a âm thì số liền trước a cũng âm.
c) Có thể kết luận gì về số liền trước của một số dương và số liền sau của một số
âm?
Bài 4 (2đ)
Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng
tổng của 31 số đó là số dương.
Bài 5 (2đ).
Cho các số tự nhiên từ 1 đến 11 được viết theo thứ tự tuỳ ý sau đó đem cộng mỗi số
với số chỉ thứ tự của nó ta được một tổng. Chứng minh rằng trong các tổng nhận được,
bao giờ cũng tìm ra hai tổng mà hiệu của chúng là một số chia hết cho 10.
Bài 6 (1,5đ):
Cho tia Ox. Trên hai nữa mặt phẳng đối nhău có bờ là Ox. Vẽ hai tia Oy và Oz sao
cho góc xOy và xOz bắng 120
0
. Chứng minh rằng:
a)
b) Tia đối của mỗi tia Ox, Oy, Oz là phân giác của góc hợp bởi hai tia còn lại.
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
ĐÁP ÁN
Bài 1 (1,5đ)
a) 5
x
= 125 5
x
= 5
3
=> x= 3
b) 3
2x
= 81 => 3
2x
= 3
4
=> 2x = 4 => x = 2
c) 5
2x-3
– 2.5
2
= 5
2
.3
5
2x
: 5
3
= 5
2
.3 + 2.5
2
5
2x
: 5
3
= 5
2
.5
5
2x
= 5
2
.5.5
3
5
2x
= 5
6
=> 2x = 6 => x=3
Bài 2. Vì là một số tự nhiên với mọi a Z nên từ < 5 ta
=> = {0,1,2,3,4}.
Nghĩa là a ={0,1,-1,2,-2,3,-3,4,-4}. Biểu diễn trên trục số cácc số này đều lớn hơn -
5 và nhỏ hơn 5 do đó -5<a<5.
Bài 3.
a) Nếu a dương thì số liền sau cũng dương.
Ta có: Nếu a dương thì a>0 số liền sau a lớn hơn a nên cũng lớn hơn 0 nên là số
dương
b) Nếu a âm thì số liền trước a cũng âm.
Ta có: Nếu a âm thì a<0 số liền trước a nhỏ hơn a nên cũng nhỏ hơn 0 nên là số âm.
Bài 4 (2đ).
Trong các số đã cho ít nhất có 1 số dương vì nếu trái lại tất cả đều là số âm thì tổng
của 5 số bất kỳ trong chúng sẽ là số âm trái với giả thiết.
Tách riêng số dương đó còn 30 số chi làm 6 nhóm. Theo đề bài tổng các số của mỗi
nhóm đều là số dương nên tổng của 6 nhóm đều là số dương và do đó tổng của 31 số đã
cho đều là số dương.
Bài 5 (2đ):
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85