SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 NGHỆ AN NĂM HỌC 2022 - 2023
Môn thi: TOÁN – BẢNG A ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (3,5 điểm).
a) Cho m,n là các số nguyên. Chứng minh rằng 2 2
mn m n chia hết cho 6.
b) Tìm tất cả các số nguyên tố p, q, r thỏa mãn 2 2 2 p 14q 2r 6pqr. Câu 2 (6,5 điểm).
a) Giải phương trình 13x 1 2x 1 7x 1 8x 1 4. 4 3 2 2
x 2x y x y 7x 9
b) Giải hệ phương trình xyx 13.
Câu 3 (1,5 điểm). Cho các số thực dương x,y,z thỏa mãn 2 2 2
x y z xy 3yz zx .
Tìm giá trị lớn nhất của biểu thức x 1 P .
2y z2 xyy 2z
Câu 4 (7,0 điểm). Cho nửa đường tròn O, đường kính BC 2R và một điểm A thay
đổi trên nửa đường tròn đó A không trùng với B và C. Vẽ AH vuông góc với BC tại
H. Gọi I, J lần lượt là tâm đường tròn nội tiếp các tam giác AHB và AHC. Đường thẳng
IJ cắt AB, AC theo thứ tự tại M và N.
a) Chứng minh tam giác AMN vuông cân. 2 2 2
b) Gọi P là giao điểm của BI và CJ. Chứng minh PA PB PC 1. CA.AB AB.BC BC.CA
c) Tìm giá trị lớn nhất của chu vi tam giác HIJ theo R.
Câu 5 (1,5 điểm). Trên một khu đất hình chữ nhật kích thước 100m120m. Người ta
muốn xây một sân bóng nhân tạo có nền đất là hình chữ nhật kích thước 25m 35m và 9
bồn hoa hình tròn đường kính 5m. Chứng minh rằng dù xây trước 9 bồn hoa ở các vị trí
như thế nào thì trên phần đất còn lại luôn tìm được một nền đất kích thước 25m 35m để xây sân bóng.
……………Hết……………
Họ và tên thí sinh………………………………… Số báo danh……………………
Chú ý: Thí sinh không được phép sử dụng máy tính bỏ túi. Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 NGHỆ AN
NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC
Môn thi: TOÁN – Bảng A
( Hướng dẫn chấm này gồm có 05 trang) Câu ĐÁP ÁN THAM KHẢO Điểm 1.a
Cho m,n là các số nguyên. Chứng minh rằng 2 2
mn m n chia hết cho 6. (2,5đ) Ta có 2 2 3 3 3 3 3 3 mn m n m n mn m n mn mn mn n m m m n n 1,0
Với mọi số nguyên a, ta có: 3 a a aa 1 a 1 0,5
Vì a 1, a, a 1 là 3 số nguyên liên tiếp nên 3
a 1 a a 1 6 a a 6 , với mọi số nguyên a. 0,5 3 m m 6 Từ đó suy ra
3 3 2 2 n m m m n n 6 mn m n 6 0,5 3 n n 6 1.b
Tìm tất cả các số nguyên tố p, q, r thỏa mãn: 2 2 2
p 14q 2r 6pqr. (1,0đ) 2 q 1 mod 3 2 14q 2mod 3
Giả sử q và r đều không chia hết cho 3 2 2 14q 2r 1 mod 3 2 r 1 mod 3 2 2r 2mod 3 0,25 q3 q 3 Suy ra 2 p 2mod
3 (Vô lý vì số chính phương chia 3 dư 0 hoặc 1) r3 r 3
Trường hợp 1: Với q 3 2 2
p 2r 18pr 7 Nếu p lẻ 2 2
p 2r lẻ và 18pr 7 chẵn nên không tồn tại p,r thỏa mãn p 2 0,25 r 5
Khi p 2, thay trở lại ta có : 2
r 18r 65 0 r 13
Trường hợp 2: Với r 3 2 2 p 14q 18pq 1 0,25 Nếu p lẻ 2 2
p 14q lẻ và 18pq
1 chẵn nên không tồn tại p, q thỏa mãn p 2 q 1
Khi p 2, thay trở lại ta có : 2 7q 18q 11 0 11 (loại) q 0,25 7
Vậy p; q; r2; 3;
5 hoặc p; q; r2; 3;1 3 . 2.a
Giải phương trình 13x 1 2x 1 7x 1 8x 14. (3,0đ) Điều kiện x 1
. Phương trình đã cho tương đương với: 26x 2 2x 1 14x 2 8x 18. 2 0,5 a 8x 2 2 1 1 4x 2 8x 1 3 2x 1 a 3b Đặt a , 0 b 0 2 2 0,5 b 2x 1 26x 2 2x 1 3 8x 1 b 3a Trang 2
Khi đó, phương trình trên trở thành: 2 2 2 2 a 3b a
b 3a b 8 a b3 8 a b 2 0,5
Với a b 2 8x 1 2x 1 2 8x 1 2x 1 2 2 8x 1 2x 1 2 0,5 3x 1 0 3x 1 2 2x 1 3x 2 1 42x 1 0,5 1 x 1 x 3
5 . Vậy phương trình đã cho có 2 nghiệm 5 x 1, x . 0,5 2 x 9x 9 14x 5 0 9 2.b 4 3 2 2
x 2x y x y 7x 9
Giải hệ phương trình (3,5đ) xyx 1 3. x xy 2 2 7x 9 1
Hệ phương trình đã cho tương đương với 2 xy x x 3 2 0,5 Thay (2) vào (1) ta có: 2 2 2x x 3 7x 9 0,5 4 3 2
4x 4x 13x 13x 0 0,5 x 0 3 4x x 1 13xx 1 0 xx 1 2 4x 13 0 x 1 1,0 Thay vào (2) ta thấy:
Khi x 0 0y 3 (không thỏa mãn). 0,5 Khi x 1 y 3
Vậy nghiệm của hệ đã cho là x;y1; 3 . 0,5 3
Cho các số thực dương x, y,z thỏa mãn 2 2 2
x y z xy 3yz zx . Tìm giá trị lớn nhất của biểu (1,5đ) thức x 1 P .
2y z2 xyy 2z +) Ta có: 2 2 2
x y z xy 3yz zx x z2 x yy 3z 2 x y y 3z x 2y 3z2
x 2y 3z 2x z 2y z x 0,5 2 4 Do đó x 1 1 . 2y z2 2y z +) Lại có: 2 1 1 1
1 3y y 2z xy y 2z x. 3y y 2z x. 2 3
x2y z 2y z 2 3 3 2 3 3 0,5 Từ (1), (2) suy ra P 1 3 2y z 2y z3 Trang 3 3 2 Đặt 2y 1 3 2 3 1 2 2 2t 9t 27
z t,t 0. Ta có P 3 3 3 t t 9 t t 9 9 9t
2 2t 6t 92t 3 2 t 2 3 2t 3 2
, t 0. Dấu " " xảy ra t 3. 3 3 9 9t 9 9t 9 0,5 x 3z x 3 Vậy 2 max P y z y 1 9 2y z 3 z 1 4.a
Chứng minh tam giác AMN vuông cân. (4,0đ) 1,0 Ta có 0
BAC 90 (góc nội tiếp chắn nửa đường tròn) 1,0
+) Tam giác ABC vuông tại A, đường cao AH suy ra 2 HA HC HA HB.HC 1 HB HA +) Lại có HI HA I HA# J HC (g.g) 2 0,5 HJ HC Từ (1) và (2) suy ra HI HB ; HJ HA 0,5 Đồng thời 0 IHJ AHB 90 HI J# HB A c.g.c. 0
HIJ HBA MIH MBH 180 0,5 Suy ra 0 0 0
IMB IHB 180 IMB 135 AMN 45 . Suy ra tam giác AMN vuông cân tại A. 0,5 4.b 2 2 2
Gọi P là giao điểm BI và CJ. Chứng minh PA PB PC 1. (2,0đ) CA.AB AB.BC BC.CA
Ta có AP là phân giác của BAC . Qua P vẽ
đường thẳng vuông góc với AP, cắt AB, AC
theo thứ tự tại D và E. Suy ra tam giác ADE vuông cân tại A. 0,5 Suy 0 BDP BPC PEC 135 Khi đó, ta có: +) PD PC D BP# P BC (g.g) và 2 PB DB.BC. (3) BD PB 0,5 +) PE PB E PC # PB C (g.g) và 2 PC BC.CE. (4) CE PC Trang 4
Đề HSG Toán 9 cấp tỉnh - Nghệ An năm 2022-2023 có đáp án
2.7 K
1.3 K lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Đề HSG Toán 9 cấp tỉnh - Nghệ An năm 2022-2023 có đáp án.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(2684 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 9
Xem thêmTài liệu bộ mới nhất

Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
NGHỆ AN
ĐỀ CHÍNH THỨC
KÌ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9
NĂM HỌC 2022 - 2023
Môn thi: TOÁN – BẢNG A
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (3,5 điểm).
a) Cho
m,n
là các số nguyên. Chứng minh rằng
22
mn m n
chia hết cho
6.
b) Tìm tất cả các số nguyên tố
p, q, r
thỏa mãn
2 22
p 14q 2r 6pqr.
Câu 2 (6,5 điểm).
a) Giải phương trình
13x12x1 7x18x14.
b) Giải hệ phương trình
4 3 22
9x
3
2x y
x
x y 7x
.
yx1
Câu 3 (1,5 điểm). Cho các số thực dương
x, y,z
thỏa mãn
222
y z xy 3yz zxx
.
Tìm giá trị lớn nhất của biểu thức
2
x1
P.
xy y 2z
2y z
Câu 4 (7,0 điểm). Cho nửa đường tròn
O
, đường kính
BC 2R
và một điểm
A
thay
đổi trên nửa đường tròn đó
A
không trùng với
B
và
C.
Vẽ
AH
vuông góc với
BC
tại
H.
Gọi
I, J
lần lượt là tâm đường tròn nội tiếp các tam giác
AHB
và
AHC.
Đường thẳng
IJ
cắt
AB, AC
theo thứ tự tại
M
và
N.
a) Chứng minh tam giác
AMN
vuông cân.
b) Gọi
P
là giao điểm của
BI
và
CJ.
Chứng minh
222
PA PB PC
1
CA.AB AB.BC BC.CA
.
c) Tìm giá trị lớn nhất của chu vi tam giác
HIJ
theo
R.
Câu 5 (1,5 điểm). Trên một khu đất hình chữ nhật kích thước
100m 120m.
Người ta
muốn xây một sân bóng nhân tạo có nền đất là hình chữ nhật kích thước
25m 35m
và
9
bồn hoa hình tròn đường kính
5m
. Chứng minh rằng dù xây trước
9
bồn hoa ở các vị trí
như thế nào thì trên phần đất còn lại luôn tìm được một nền đất kích thước
25m 35m
để
xây sân bóng.
……………Hết……………
Họ và tên thí sinh………………………………… Số báo danh……………………
Chú ý: Thí sinh không được phép sử dụng máy tính bỏ túi.

Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
NGHỆ AN
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9
NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC
Môn thi: TOÁN – Bảng A
( Hướng dẫn chấm này gồm có 05 trang)
Câu ĐÁP ÁN THAM KHẢO Điểm
1.a
(2,5đ)
Cho
m,n
là các số nguyên. Chứng minh rằng
22
mn m n
chia hết cho
6.
Ta có
22 3 3 3 3 3 3
mn m n m n mn m n mn mn mn n m m m n n
1,0
Với mọi số nguyên a, ta có:
3
a a aa 1 a 1
0,5
Vì
a 1,a,a 1
là 3 số nguyên liên tiếp nên
3
a 1a a 1 6 a a 6
, với mọi số nguyên a.
0,5
Từ đó suy ra
3
3
m6
nn
m
6
3
23 2
nm m mn n 6 mnm 6
n
0,5
1.b
(1,0đ)
Tìm tất cả các số nguyên tố
p, q, r
thỏa mãn:
2 22
p 14q 2r 6pqr.
Giả sử
q
và
r
đều không chia hết cho 3
2
2
q 1 mod3
r 1 mod3
2
22
2
14q 2 mod3
14q 2r 1 mod3
2r 2 mod3
0,25
Suy ra
2
p 2 mod3
(Vô lý vì số chính phương chia 3 dư 0 hoặc 1)
q3 q 3
r3 r 3
Trường hợp 1: Với
q3
22
p 2r 18 pr 7
Nếu
p
lẻ
22
p 2r
lẻ và
18 pr 7
chẵn nên không tồn tại
p,r
thỏa mãn
p2
0,25
Khi
p 2,
thay trở lại ta có :
2
r5
r 18r 65 0
r 13
Trường hợp 2: Với
r3
22
p 14q 18 pq 1
Nếu
p
lẻ
22
p 14q
lẻ và
18 pq 1
chẵn nên không tồn tại
p, q
thỏa mãn
p2
0,25
Khi
p 2,
thay trở lại ta có :
2
q1
7q 18q 11 0
11
q
7
(loại)
Vậy
p; q; r 2; 3; 5
hoặc
p; q; r 2; 3;13
.
0,25
2.a
(3,0đ)
Giải phương trình
13x 1 2x 1 7x 1 8x 1 4.
Điều kiện
x
1
.
2
Phương trình đã cho tương đương với:
26x 2 2x 1 14x 2 8x 1 8.
0,5
Đặt
0
a 8x 1
a
b
,b
x
0
21
22
22
314x 2 8x 1 3 2x 1 a
26x 2 2x 1 3 8x 1 b 3a
b
0,5

Trang 3
Khi đó, phương trình trên trở thành:
3
22 22
a 3ba b 3ab8 ab 8 ab2
0,5
Với
a b 2 8x 1 2x 1 2 8x 1 2x 1 2
2
8x 1 2x 1 2
0,5
2
3x 1
3x122x1
3x1 42x1
0
0,5
2
x1
x
5
x
9x 14x 5
1
3
0
9
. Vậy phương trình đã cho có 2 nghiệm
5
x 1, x .
9
0,5
2.b
(3,5đ)
Giải hệ phương trình
4 3 22
9x
3
2x y
x
x y 7x
.yx1
Hệ phương trình đã cho tương đương với
2
2
2
x xy 1
xy x 3
7x 9
x2
0,5
Thay (2) vào (1) ta có:
2
2
2x x3 7x9
0,5
43 2
4x 4x 13x 13x 0
0,5
32
x0
4x x 1 13x x 1 0 x x 1 4x 13 0
x1
1,0
Thay vào (2) ta thấy:
Khi
x0
0y 3
(không thỏa mãn).
0,5
Khi
x1 y3
Vậy nghiệm của hệ đã cho là
x; y 1; 3 .
0,5
3
(1,5đ)
Cho các số thực dương
x, y,z
thỏa mãn
222
y z xy 3yz zx
x
. Tìm giá trị lớn nhất của biểu
thức
2
x1
P.
xy y 2z
2y z
+) Ta có:
2
222
x x y y 3zy z xy 3yz zx x z
2
2
x
x 2y 3z
x 2y 3z x z 2y z
4
x y y 3z
2
2
Do đó
2
x1
1
2y z
2y z
.
0,5
+) Lại có:
2
1 1 3y y 2z
xy y 2z x. 3y y 2z x.
3 32
32
11
x 2y z 2y z 2
33
Từ (1), (2) suy ra
3
P
13
2y z
2y z
0,5
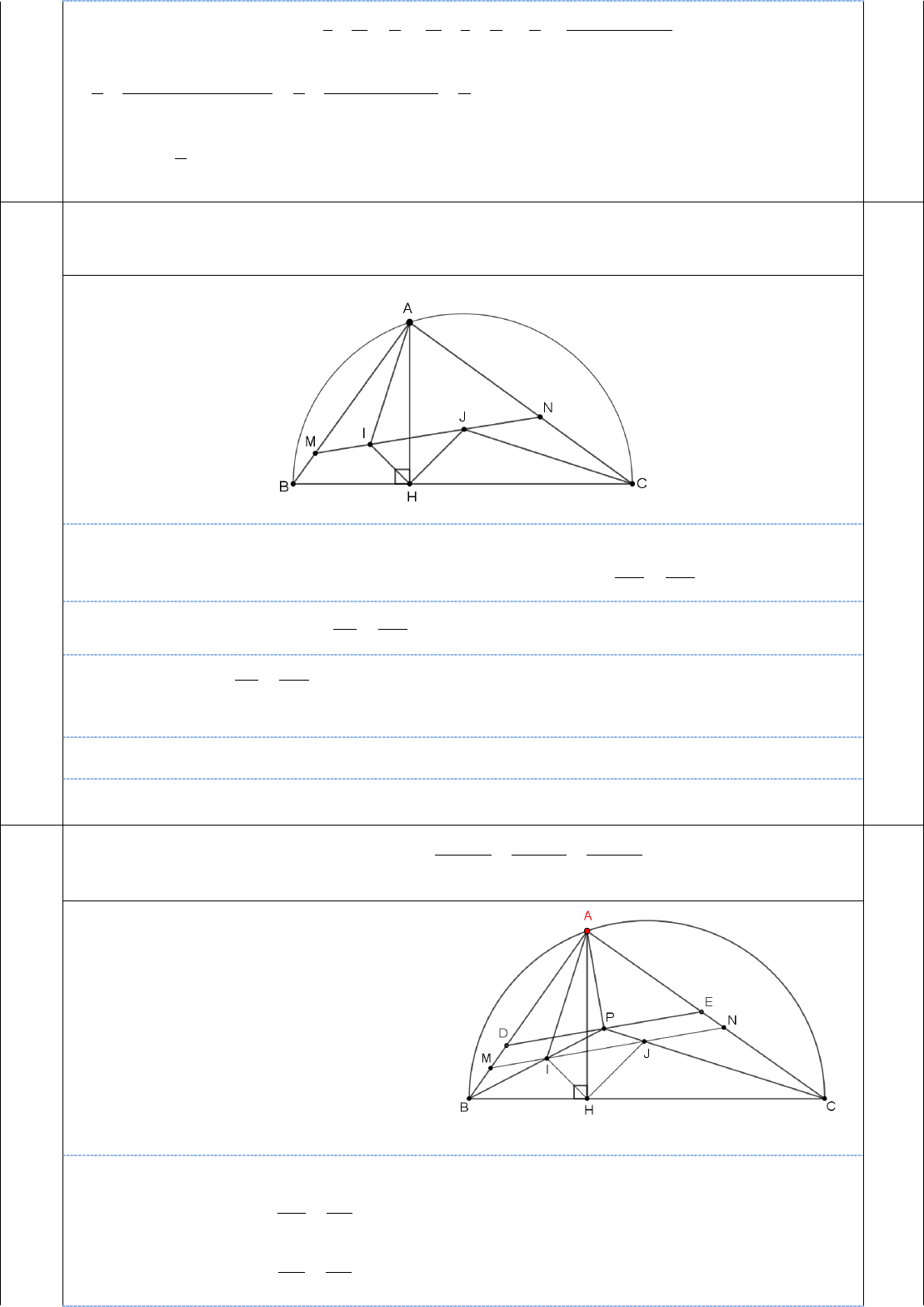
Trang 4
Đặt
2y z t,t 0.
Ta có
32
33 3
1 3 2 3 1 2 2 2t 9t 27
P
t t 9 t t 9 9 9t
2
2
33
2
, t 0.
t 6t 9 2t 3
t
9
3 2t 3
22
9 9t 9 9t
Dấu
""
xảy ra
t 3.
Vậy
x3z x3
2
max P y z y 1
9
2y z 3 z 1
0,5
4.a
(4,0đ)
Chứng minh tam giác
AMN
vuông cân.
1,0
Ta có
0
BAC 90
(góc nội tiếp chắn nửa đường tròn)
+) Tam giác ABC vuông tại A, đường cao AH suy ra
2
HA HC
HA HB.HC 1
HB HA
1,0
+) Lại có
HI HA
IHA JHC (g.g) 2
HJ HC
#
0,5
Từ (1) và (2) suy ra
HI HB
;
HJ HA
Đồng thời
0
IHJ AHB 90 HIJ HBA c.g.c #
.
0,5
0
HIJ HBA MIH MBH 180
0,5
Suy ra
00 0
IMB IHB 180 IMB 135 AMN 45
. Suy ra tam giác AMN vuông cân tại A.
0,5
4.b
(2,0đ)
Gọi
P
là giao điểm
BI
và
CJ.
Chứng minh
222
PA PB PC
1
CA.AB AB.BC BC.CA
.
Ta có AP là phân giác của
BAC
. Qua P vẽ
đường thẳng vuông góc với AP, cắt AB, AC
theo thứ tự tại D và E. Suy ra tam giác ADE
vuông cân tại A.
Suy
0
BDP BPC PEC 135
0,5
Khi đó, ta có:
+)
PD PC
DBP PBC (g.g)
BD PB
#
và
2
PB DB.BC.
(3)
+)
PE PB
EPC PBC (g.g)
CE PC
#
và
2
PC BC.CE.
(4)
0,5
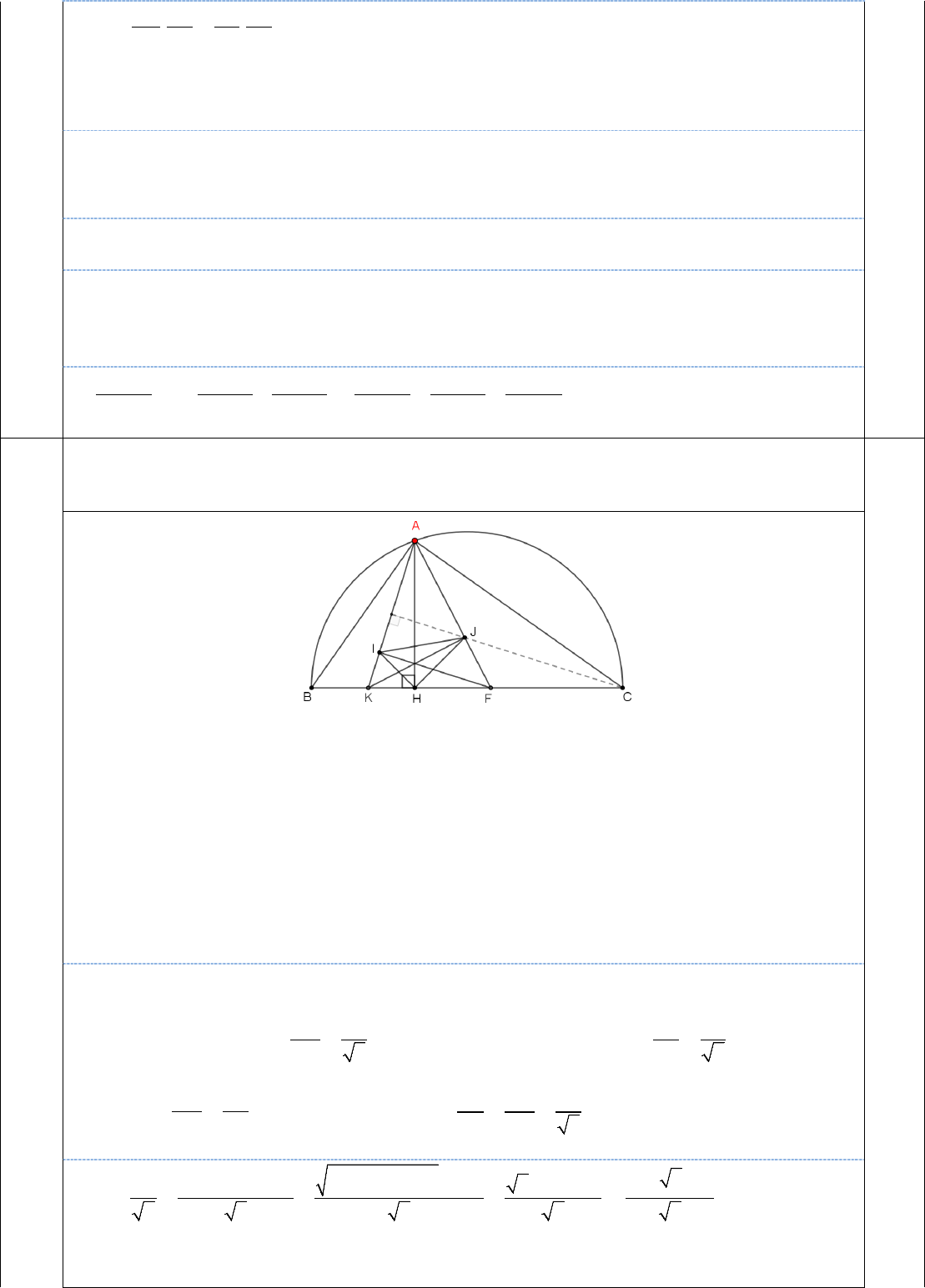
Trang 5
Suy ra:
2
PD PE PC PB
. . 1 PD.PE BD.CE BD.CE PD.PE PE
BD CE PB PC
(do PD = PE) (5)
Áp dụng định lí Pytago cho tam giác PAE vuông tại P ta có:
2222
PA AE PE AE BD.CE AE.AD BD.CE
, theo (5).
0,5
AC CE AB BD BD.CE
AB.AC BD.AC AB.CE
0,5
2
PA BC AB.AC.BC BC.BD AC AB. EC.BC
2 22
PA BC AB.AC.BC PB .AC PC .AB
, do kết hợp với (3) và (4).
0,5
2 22
PA PB PC
1
AB.AC BC.AB AC.BC
222
PA PB PC
1
AB.AC AB.BC BC.CA
0,5
4c
(1,0đ)
Tìm giá trị lớn nhất của chu vi tam giác
HIJ
theo
R.
Gọi K và F theo thứ tự là giao điểm của
AI; AJ
với BC.
Ta có
F
AFC FAC ACF
AFC BAF
BAF H AH
A
AF B
B
cân tại B
BF BA
Tương tự
CAK
cân tại C
CK CA
Khi đó:
KF CK CF CK BC BF AC AB BC
0,25
Xét tam giác
KAJ
có
0
KAJ 45 ;JA JK
(do J nằm trên CJ là trung trực đoạn AK)
KAJ
vuông cân tại
J
AJ 1
AK
2
. Tương tự
FAI
vuông cân tại
AI 1
F
AF
2
Từ đó suy ra
AJ AI
AK AF
IJ AJ 1
AJI AKF c.g.c
FK AK
2
#
0,25
22
2 AB AC BC
FK AB AC BC 2.BC BC
IJ
22 2 2
BC 2 1
2
.
Đẳng thức xảy ra khi AB = AC .
0,25