SỞ GD&ĐT VĨNH PHÚC KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS NĂM HỌC 2022-2023
ĐỀ THI MÔN: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian giao đề) 2 2 2 2
Câu 1. Cho biểu thức x y x y P = ( − − .
x + y)(1− y) (x + y)(1+ x) (1+ x)(1− y) a. Rút gọn biểu thức . P
b. Tìm các số nguyên x, y thỏa mãn P = 2.
Câu 2. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d ) 2
: y = 2x − m +1, (d : y = x − m − m 2 ) 2 1 và (d ) 2
: y = 3x − m − m + 2. Biết (d cắt (d và (d lần lượt tại (
A x ; y ) và B(x ; y .) 3 ) 2 ) 1 ) 3 1 1 2 2 Tìm m để 2 2
(x − x ) + (y − y ) = 320. 1 2 1 2
Câu 3. Cho đa thức P(x) 3 2
= x + ax + bx + .
c Biết P(x) chia hết cho (x − 2) và P(x) chia cho ( 2 x − ) 1
thì dư là 2 .x Tính P(3).
Câu 4. Giải phương trình 2
2x −3 + 5 − 2x = 3x −12x +14 . 3
x + 7y = (x + y)2 2 + x y + 7x + 4
Câu 5. Giải hệ phương trình (x, y ∈) . 2 2 3
x + y + 8y + 4 = 8x
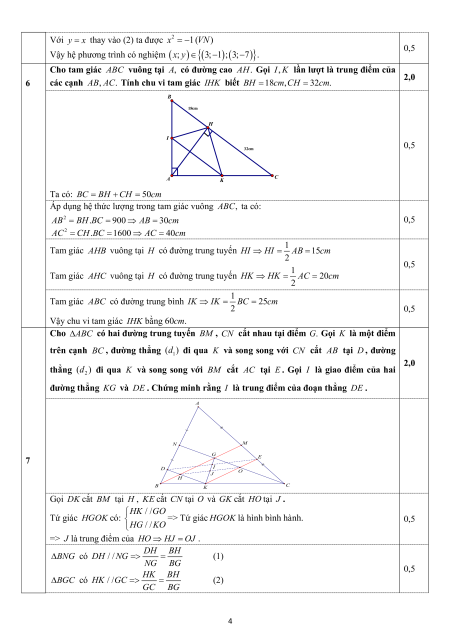
Câu 6. Cho tam giác ABC vuông tại ,
A có đường cao là AH. Gọi I, K lần lượt là trung điểm của các
cạnh AB, AC. Tính chu vi tam giác IHK biết BH =18c , m CH = 32c . m
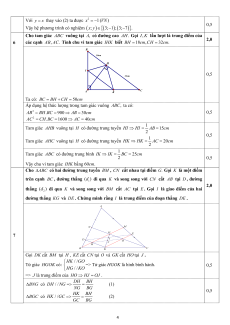
Câu 7. Cho tam giác ABC có hai đường trung tuyến BM , CN cắt nhau tại điểm .
G Gọi K là một
điểm trên cạnh BC, đường thẳng (d )
1 đi qua K và song song với CN cắt AB tại D, đường thẳng (d )
2 đi qua K và song song với BM cắt AC tại E. Gọi I là giao điểm của hai đường thẳng KG và
DE. Chứng minh rằng I là trung điểm của đoạn thẳng DE.
Câu 8. Cho hình thang ABCD có đáy nhỏ là AB và BC = B .
D Gọi H là trung điểm của đoạn thẳng .
CD Đường thẳng (d) đi qua điểm H cắt các đường thẳng AC, AD lần lượt tại E, F sao cho D nằm
giữa A và F. Chứng minh rằng = DBF EBC.
Câu 9. Một cửa hàng bán bưởi Đoan Hùng với giá bán mỗi quả là 50000 đồng. Với giá bán này thì mỗi
ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi
quả 1000 đồng thì số bưởi bán tăng thêm được là 10 quả mỗi ngày. Xác định giá bán để cửa hàng thu
được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả bưởi là 30000 đồng.
Câu 10. Cho ba số thực dương a, , b c thỏa mãn 2 2 2
a + b + c =1. Chứng minh 3 3 3 a b + c + > 2. 2 2 2
b −bc + c a
---------- Hết ----------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………………….…............. Số báo danh:…….………. 1
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 9 NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM MÔN: TOÁN
( Hướng dẫn chấm gồm 05 trang)
I) Hướng dẫn chung:
1) Hướng dẫn chấm chỉ nêu một cách giải với những ý cơ bản, nếu thí sinh làm bài không
theo cách nêu trong hướng dẫn chấm nhưng vẫn đúng thì cho đủ số điểm từng phần như thang điểm quy định.
2) Việc chi tiết hoá thang điểm (nếu có) trong hướng dẫn chấm phải đảm bảo không làm sai lệch
hướng dẫn chấm và phải được thống nhất thực hiện với tất cả giám khảo.
3) Điểm toàn bài tính đến 0,25 điểm. Sau khi cộng điểm toàn bài, giữ nguyên kết quả.
4) Với bài hình học nếu học sinh không vẽ hình phần nào thì không cho điểm phần đó.
II) Đáp án và thang điểm:
Câu Nội dung trình bày Điểm 1 2 2 2 2 Cho biểu thức x y x y P = − − .
(x + y)(1− y) (x + y)(1+ x) (1+ x)(1− y) 1,5
a. Rút gọn biểu thức . P x ≠ −y ≠ − ĐK: x 1 0,25 y ≠ 1 2 x ( + x) 2 − y ( − y) 2 2 1 1
− x y (x + y) ( 3 3 x + y ) + ( 2 2 x − y ) 2 2
− x y (x + y) P = ( = 0,5
x + y)(1+ x)(1− y)
(x + y)(1+ x)(1− y) 2 2 2 2
(x + y)(x − y + x − xy + y − x y ) = 0,25
(x + y)(1+ x)(1− y)
(x + y)(1+ x)(1− y)(x + xy − y) = (
x + y)(1+ x)(1− y) 0,25
= x + xy − y 0,25
b. Tìm các số nguyên x, y thỏa mãn phương trình P = 2. 1,0
P = 2 ⇔ x( y + ) 1 = y + 2 0,25 y ≠ 1 − ⇔ 0,25 1 x =1+ y +1
Vì x, y ∈ nên ( y + )
1 là ước của 1⇒ y +1 =1 hoặc y +1 = 1 − 0,25 x = 2 x = 0 Vậy hoặc 0,25 y = 0 y = 2 − 2
Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng (d ) 2
: y = 2x − m +1, 1 (d ) 2
: y = x − m − ,
m và (d : y = 3x − m − m + 2. Biết (d cắt (d và (d lần lượt tại 2,0 3 ) 2 ) 1 ) 3 ) 2 2 ( A x ; y )
B(x ; y .)
(x − x ) + (y − y ) = 320. 1 1 và 2 2
Tìm m để 2 2 1 2 1 2 + Ta có
(d : y = 2x − m +1 cắt (d : y = x − m − ,
m tại điểm A( 2 1 − − ;
m −m − 2m − ) 0,5 2 ) 2 1 ) 2 1 . (d ) 2
: y = 2x − m +1 cắt (d : y = 3x − m − m + 2. tại điểm B( 2 1 − + ;
m −m + 2m − ) 3 ) 2 1 1 . 0,5 2
Ta có (x − x )2 + ( y − y )2 = 320 ⇒ ( 2 − m)2 + ( 4 − m)2 = 320. 1 2 1 2 0,5 2 2 2
⇔ 4m +16m = 320 ⇔ m =16 ⇔ m = 4 ± . Vậy m = 4 ± . 0,5
Cho đa thức P(x) 3 2
= x + ax + bx + .
c Biết P(x) chia hết cho (x − 2) và P(x) chia cho 3 2,0
( 2x − )1 thì dư là 2x. Tính P(3).
Vì P(x) chia hết cho (x − 2) nên P(2) = 8 + 4a + 2b + c = 0 ⇔ c = 8
− − 4a − 2b 0,5
Do P(x) chia cho ( 2 x − ) thì dư
P x − x chia hết cho ( 2 x − ), suy ra 1 2x nên ( ) 2 1 P( ) 1 − 2 = 0
a + b + c =1 0,5 ⇔ P (− ) 1 + 2 = 0
a − b + c = 1 − 10 3a + b = 9 − a − = 10 + Thay c = 8
− − 4a − 2b ta có hệ ⇔ 3 ⇒ c = . 3 0,5 a + 3b = 7 − 3 b =1 ⇒ P(x) 3 10 2 10 10 = x − x + x + ⇒ P(3) = . Vậy P( ) 10 3 = . 3 3 3 3 0,5 x − +
− x = x − x + 4 Giải phương trình 2 2 3 5 2 3 12 14 . 2,0 Điều kiện: 3 5 ≤ x ≤ 0,5 2 2
Áp dụng Bunnhiacopski, ta có: 2 2
VT =1. 2x − 3 +1. 5 − 2x ≤ (1 +1 )(2x − 3+ 5 − 2x) = 2 (1) 0,5 2 2
VP = 3x −12x +14 = 3(x − 2) + 2 ≥ 2, x ∀ (2) 0,5 Phương trình 2
2x −3 + 5 − 2x = 3x −12x +14 có nghiệm
⇔ Dấu “=” ở (1) và (2) đồng thời xảy ra. x − = − x 0,5 ⇔ 2 3 5 2 ⇔ x = 2 . x − 2 = 0
Vậy phương trình có nghiệm x = 2 . 3
x + 7y = (x + y)2 2 + x y + 7x + 4
Giải hệ phương trình
(x, y ∈) . 2 2 3 2,0
x + y + 8y + 4 = 8x 3
x + 7y = (x + y)2 2
+ x y + 7x + 4 (1) HPT ⇔ 2 2 4 = 3
− x − y −8y + 8x (2) 0,5
Thay (2) vào (1) ta được 3
x + y = (x + y)2 2 2 2 7
+ x y + 7x − 3x − y −8y + 8x 5 x = y
(x y)( 2x 2x 15) 0 ⇔ − + − = ⇔ x = 3 0,5 x = 5 − y = 1 −
Với x = 3 thay vào (2) ta được 2
y + 8y + 7 = 0 ⇔ y = 7 − 0,5 Với x = 5
− thay vào (2) ta được 2
y + 8y +119 = 0 (VN) 3
Với y = x thay vào (2) ta được 2 x = 1( − VN) 0,5
Vậy hệ phương trình có nghiệm ( ; x y)∈ ( { 3;− )1;(3; 7 − )}.
Cho tam giác ABC vuông tại ,
A có đường cao AH. Gọi I, K lần lượt là trung điểm của 6
các cạnh AB, AC. Tính chu vi tam giác IHK biết BH =18c , m CH = 32c . m 2,0 B 18cm H I 32cm 0,5 A K C
Ta có: BC = BH + CH = 50cm
Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có: 2
AB = BH.BC = 900 ⇒ AB = 30cm 0,5 2
AC = CH.BC =1600 ⇒ AC = 40cm
Tam giác AHB vuông tại H có đường trung tuyến 1
HI ⇒ HI = AB =15cm 2 0,5
Tam giác AHC vuông tại H có đường trung tuyến 1
HK ⇒ HK = AC = 20cm 2
Tam giác ABC có đường trung bình 1
IK ⇒ IK = BC = 25cm 2 0,5
Vậy chu vi tam giác IHK bằng 60cm. Cho A
∆ BC có hai đường trung tuyến BM , CN cắt nhau tại điểm .
G Gọi K là một điểm
trên cạnh BC , đường thẳng (d )1 đi qua K và song song với CN cắt AB tại D , đường 2,0 thẳng (d )
2 đi qua K và song song với BM cắt AC tại E . Gọi I là giao điểm của hai
đường thẳng KG và DE . Chứng minh rằng I là trung điểm của đoạn thẳng DE . A N M 7 G E I D J O H B C K
Gọi DK cắt BM tại H , KE cắt CN tại O và GK cắt HO tại J . HK / /GO
Tứ giác HGOK có:
=> Tứ giác HGOK là hình bình hành. 0,5 HG / /KO
=> J là trung điểm của HO ⇒ HJ = OJ . B ∆ NG có / / DH BH DH NG => = (1) NG BG 0,5 B ∆ GC có / / HK BH HK GC => = (2) GC BG 4
Đề HSG Toán 9 cấp tỉnh - Vĩnh Phúc năm 2022-2023 có đáp án
2.1 K
1.1 K lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Đề HSG Toán 9 cấp tỉnh - Vĩnh Phúc năm 2022-2023 có đáp án.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(2113 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 9
Xem thêmTài liệu bộ mới nhất

1
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS NĂM HỌC 2022-2023
ĐỀ THI MÔN: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Câu 1. Cho biểu thức
( )
( )
(
)(
) (
)
( )
2 2 22
1 1 11
x y xy
P
xy y xy x x y
=−−
+− ++ +−
.
a. Rút gọn biểu thức
.
P
b. Tìm các số nguyên
,xy
thỏa mãn
2.P =
Câu 2. Trong mặt phẳng tọa độ Oxy, cho ba đường thẳng
( )
2
1
: 2 1,
d y xm=−+
(
)
2
2
:
d y xm m
=−−
và
( )
2
3
: 3 2.d y xm m= − −+
Biết
( )
1
d
cắt
(
)
2
d
và
(
)
3
d
lần lượt tại
11
();Ax y
và
22
.
;
()
Bx y
Tìm m để
22
12 12
320.( )( )
xx yy+−
−
=
Câu 3. Cho đa thức
( )
32
.P x x ax bx c=+ ++
Biết
()
Px
chia hết cho
( )
2x −
và
( )
Px
chia cho
( )
2
1x −
thì dư là
2.x
Tính
(
)
3.
P
Câu 4. Giải phương trình
2
2 3 5 2 3 12 14x xx x−+ − = − +
.
Câu 5. Giải hệ phương trình
( )
2
32
22
7 74
(, )
3 8 48
x y x y xy x
xy
xy y x
+=+ + ++
∈
+ + +=
.
Câu 6. Cho tam giác
ABC
vuông tại
,A
có đường cao là
.AH
Gọi
,IK
lần lượt là trung điểm của các
cạnh
,.AB AC
Tính chu vi tam giác
IHK
biết
18 , 32 .
BH cm CH cm= =
Câu 7. Cho tam giác
ABC
có hai đường trung tuyến
,BM
CN
cắt nhau tại điểm
.G
Gọi
K
là một
điểm trên cạnh
,
BC
đường thẳng
1
()d
đi qua
K
và song song với
CN
cắt
AB
tại
,D
đường thẳng
2
()d
đi qua
K
và song song với
BM
cắt
AC
tại
.
E
Gọi
I
là giao điểm của hai đường thẳng
KG
và
.
DE
Chứng minh rằng
I
là trung điểm của đoạn thẳng
.DE
Câu 8. Cho hình thang
ABCD
có đáy nhỏ là
AB
và
.BC BD=
Gọi
H
là trung điểm của đoạn thẳng
.CD
Đường thẳng
()d
đi qua điểm
H
cắt các đường thẳng
,AC AD
lần lượt tại
,EF
sao cho
D
nằm
giữa
A
và
.
F
Chứng minh rằng
.DBF EBC=
Câu 9. Một cửa hàng bán bưởi Đoan Hùng với giá bán mỗi quả là 50000 đồng. Với giá bán này thì mỗi
ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi
quả 1000 đồng thì số bưởi bán tăng thêm được là 10 quả mỗi ngày. Xác định giá bán để cửa hàng thu
được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu cho mỗi quả bưởi là 30000 đồng.
Câu 10. Cho ba số thực dương
,,abc
thỏa mãn
222
1.abc++=
Chứng minh
3 33
2 22
2.
a bc
b bc c a
+
+>
−+
---------- Hết ----------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………………………….…............. Số báo danh:…….……….
ĐỀ CHÍNH THỨC

2
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 9 NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM MÔN: TOÁN
( Hướng dẫn chấm gồm 05 trang)
I) Hướng dẫn chung:
1) Hướng dẫn chấm chỉ nêu một cách giải với những ý cơ bản, nếu thí sinh làm bài không
theo cách nêu trong hướng dẫn chấm nhưng vẫn đúng thì cho đủ số điểm từng phần như thang
điểm quy định.
2) Việc chi tiết hoá thang điểm (nếu có) trong hướng dẫn chấm phải đảm bảo không làm sai lệch
hướng dẫn chấm và phải được thống nhất thực hiện với tất cả giám khảo.
3) Điểm toàn bài tính đến 0,25 điểm. Sau khi cộng điểm toàn bài, giữ nguyên kết quả.
4) Với bài hình học nếu học sinh không vẽ hình phần nào thì không cho điểm phần đó.
II) Đáp án và thang điểm:
Câu
Nội dung trình bày
Điểm
1
Cho biểu thức
(
)
(
)
( )
(
)
( )
(
)
2 2 22
1 1 11
x y xy
P
xy y xy x x y
=−−
+− ++ +−
.
a. Rút gọn biểu thức
.P
1,5
ĐK:
1
1
xy
x
y
≠−
≠−
≠
0,25
( ) ( )
( )
(
)( )
( )
2 2 22
11
11
x x y y xy x y
P
xy x y
+− −− +
=
++−
(
) (
)
( )
(
)(
)(
)
3 3 2 2 22
11
x y x y xy x y
xy x y
++−− +
=
++−
0,5
( )
(
)
(
)
(
)(
)
2 2 22
11
x y x y x xy y x y
xy x y
+ −+ − + −
=
++−
0,25
(
)( )
( )( )
( )( )( )
11
11
xy x yxxyy
xy x y
+ + − +−
=
++−
0,25
x xy y=+−
0,25
b. Tìm các số nguyên
,
xy
thỏa mãn phương trình
2.P =
1,0
( )
2 12P xy y=⇔ +=+
0,25
1
1
1
1
y
x
y
≠−
⇔
= +
+
0,25
Vì
,xy∈
nên
( )
1y +
là ước của
1 11y
⇒ +=
hoặc
11
y +=−
0,25
Vậy
2
0
x
y
=
=
hoặc
0
2
x
y
=
= −
0,25
2
Trong mặt phẳng tọa độ
Oxy,
cho ba đường thẳng
( )
2
1
: 2 1,d y xm=−+
( )
2
2
:,d y xm m=−−
và
( )
2
3
: 3 2.d y xm m= − −+
Biết
( )
1
d
cắt
( )
2
d
và
( )
3
d
lần lượt tại
11
();Ax y
và
22
.;()Bx y
Tìm m để
22
12 12
320.( )( )xx yy+−− =
2,0
+ Ta có
( )
2
1
:2 1d y xm=−+
cắt
( )
2
2
:,d y xm m=−−
tại điểm
( )
2
1 ; 2 1.A mm m−− − − −
0,5
( )
2
1
:2 1d y xm=−+
cắt
( )
2
3
: 3 2.d y xm m= − −+
tại điểm
( )
2
1; 21.B mm m−+ − + −
0,5

3
Ta có
( ) ( ) ( ) ( )
2 2 22
12 12
320 320.24mmxx yy− −−+− = ⇒ + =
0,5
22 2
4 16 320 16 4mm m m⇔ + = ⇔ =⇔=±
. Vậy
4m = ±
.
0,5
3
Cho đa thức
( )
32
.P x x ax bx c=+ ++
Biết
()Px
chia hết cho
( )
2x −
và
( )
Px
chia cho
(
)
2
1
x
−
thì dư là
2x
. Tính
( )
3.P
2,0
Vì
( )
Px
chia hết cho
(
)
2x
−
nên
(
)
2 84 2 0 84 2
P a bc c a b
= + + + = ⇔ =−− −
0,5
Do
( )
Px
chia cho
(
)
2
1
x −
thì dư
2
x
nên
(
)
2Px x
−
chia hết cho
(
)
2
1x
−
, suy ra
( )
( )
1 20
1
1
1 20
P
abc
abc
P
−=
++=
⇔
−+=−
−+=
0,5
+ Thay
84 2
c ab=−− −
ta có hệ
10
39
10
.
3
33 7
3
1
ab
a
c
ab
b
−
+=−
=
⇔ ⇒=
+=−
=
0,5
(
)
32
10 10 10
(3) .
33 3
Px x x x P
⇒ = − ++ ⇒ =
Vậy
( )
10
3.
3
P =
0,5
4
Giải phương trình
2
2 3 5 2 3 12 14x xx x−+ − = − +
.
2,0
Điều kiện:
35
22
x≤≤
0,5
Áp dụng Bunnhiacopski, ta có:
22
1. 2 3 1. 5 2 (1 1 )(2 3 5 2 ) 2VT x x x x
= −+ − ≤ + −+− =
(1)
0,5
22
3 12 14 3( 2) 2 2
VP x x x
= − + = − +≥
,
x∀
(2)
0,5
Phương trình
2
2 3 5 2 3 12 14x xx x−+ − = − +
có nghiệm
⇔
Dấu “=” ở (1) và (2) đồng thời xảy ra.
⇔
2 3 52
2
20
xx
x
x
−= −
⇔=
−=
.
Vậy phương trình có nghiệm
2x =
.
0,5
5
Giải hệ phương trình
( )
2
32
22
7 74
(, )
3 8 48
x y x y xy x
xy
xy y x
+=+ + ++
∈
+ + +=
.
2,0
( )
2
32
22
7 7 4 (1)
4 3 8 8 (2)
x y x y xy x
HPT
xy yx
+=+ + ++
⇔
=− −−+
Thay (2) vào (1) ta được
( )
2
3 2 22
7 73 88x y x y xy x x y y x+ =+ + +− −−+
0,5
( )
( )
2
2 15 0 3
5
xy
xyx x x
x
=
⇔− +− =⇔=
= −
0,5
Với
3x =
thay vào (2) ta được
2
1
8 70
7
y
yy
y
= −
+ +=⇔
= −
Với
5x = −
thay vào (2) ta được
2
8 119 0 ( )y y VN++ =
0,5
4
Với
=yx
thay vào (2) ta được
2
1( )x VN= −
Vậy hệ phương trình có nghiệm
( ) ( ) ( )
{ }
; 3; 1 ; 3; 7 .xy∈− −
0,5
6
Cho tam giác
ABC
vuông tại
,A
có đường cao
.AH
Gọi
,IK
lần lượt là trung điểm của
các cạnh
,.AB AC
Tính chu vi tam giác
IHK
biết
18 , 32 .BH cm CH cm= =
2,0
Ta có:
50BC BH CH cm=+=
0,5
Áp dụng hệ thức lượng trong tam giác vuông
,ABC
ta có:
2
. 900 30AB BH BC AB cm= =⇒=
2
. 1600 40AC CH BC AC cm= = ⇒=
0,5
Tam giác
AHB
vuông tại
H
có đường trung tuyến
1
15
2
HI HI AB cm⇒= =
Tam giác
AHC
vuông tại
H
có đường trung tuyến
1
20
2
HK HK AC cm⇒= =
0,5
Tam giác
ABC
có đường trung bình
1
25
2
IK IK BC cm⇒= =
Vậy chu vi tam giác
IHK
bằng 60cm.
0,5
7
Cho
ABC∆
có hai đường trung tuyến
BM
,
CN
cắt nhau tại điểm
.G
Gọi
K
là một điểm
trên cạnh
BC
, đường thẳng
1
()d
đi qua
K
và song song với
CN
cắt
AB
tại
D
, đường
thẳng
2
()d
đi qua
K
và song song với
BM
cắt
AC
tại
E
. Gọi
I
là giao điểm của hai
đường thẳng
KG
và
DE
. Chứng minh rằng
I
là trung điểm của đoạn thẳng
DE
.
2,0
Gọi
DK
cắt
BM
tại
H
,
KE
cắt
CN
tại
O
và
GK
cắt
HO
tại
J
.
Tứ giác
HGOK
có:
//
//
HK GO
HG KO
=> Tứ giác
HGOK
là hình bình hành.
=>
J
là trung điểm của
HO HJ OJ⇒=
.
0,5
BNG∆
có
//
DH BH
DH NG
NG BG
=>=
(1)
BGC∆
có
//
HK BH
HK GC
GC BG
=>=
(2)
0,5
32cm
18cm
K
I
H
A
C
B
J
I
O
H
E
D
G
N
M
B
C
A
K
5
Từ (1) và (2) ta có
1
2
DH HK DH NG
NG GC HK GC
==>==
(*) (Do
G
là trọng tâm
ABC∆
).
Cmtt ta có:
CMG∆
có
//
OE OC
OE GM
GM CG
=>=
(3)
CBG∆
có
//
OK OC
OK BG
GB CG
=>=
(4)
Từ (3) và (4) =>
1
2
OE OK OE GM
GM GB OK GB
==>= =
(**)
0,5
Từ (*) và (**)
1
2
DH OE
DKE
HK OK
=> = = =>∆
có
//OH DE
.
Lại có
J
là trung điểm
HO I
⇒
là trung điểm
DE
.
0,5
8
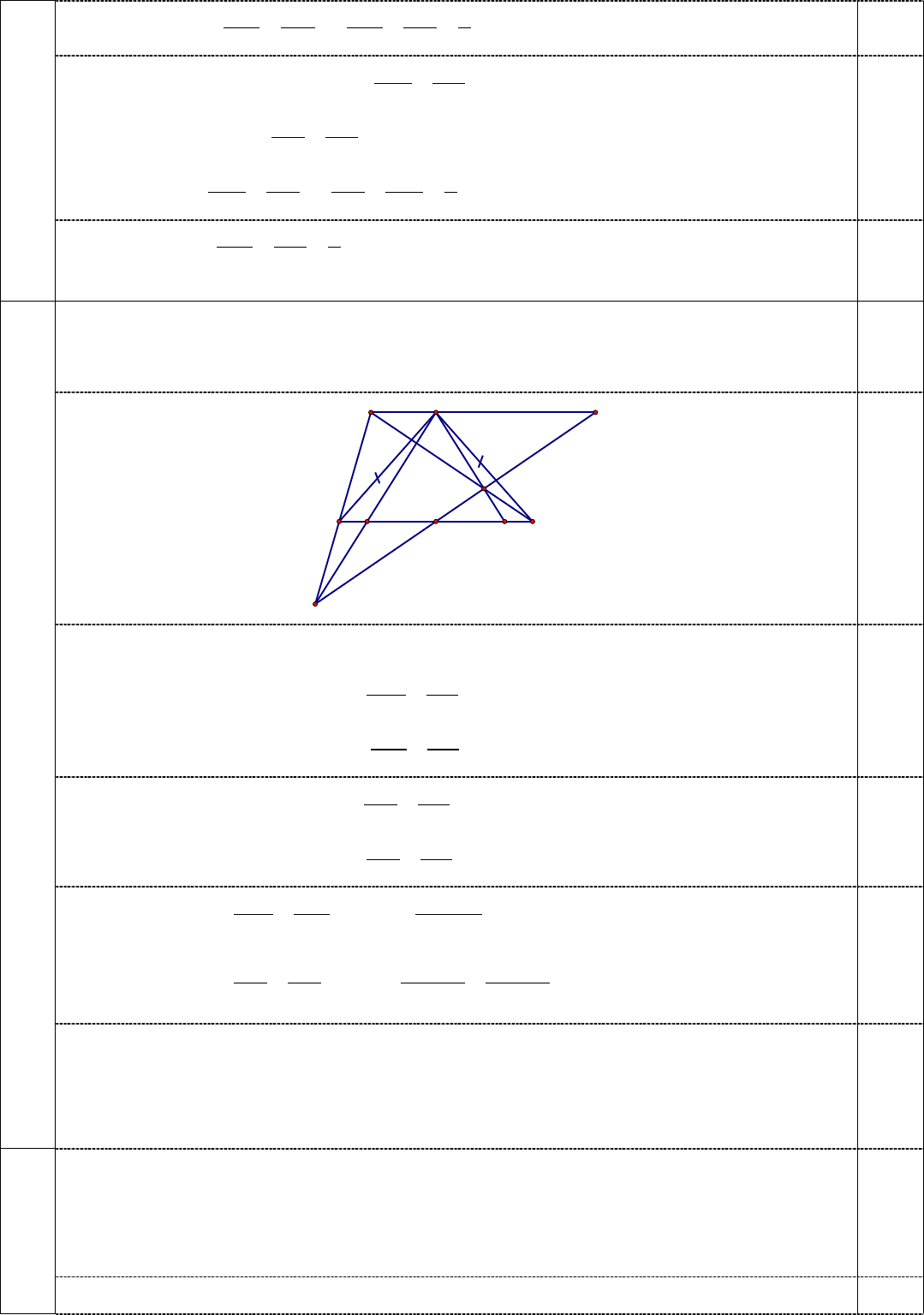
Cho hình thang
ABCD
có đáy nhỏ là
AB
và
.
BC BD
=
Gọi
H
là trung điểm của đoạn
thẳng
.CD
Đường thẳng
()d
đi qua
H
cắt
,AC AD
lần lượt tại
,EF
sao cho
D
nằm giữa
A
và
.F
Chứng minh rằng
.DBF EBC=
2,0
Gọi
M
là giao điểm của
BF
và
,CD N
là giao của
BE
và
,CD K
là giao của
EF
và
.AB
Xét tam giác
FAB
có
( )
// 1
DM FD
DM AB
AB FA
⇒=
Xét tam giác
FAK
có
( )
// 2
DH FD
DH AK
AK FA
⇒=
0,5
Xét tam giác
ENC
có
( )
// 3
NC EC
AB NC
AB EA
⇒=
Xét tam giác
EHC
có
( )
// 4
HC EC
AK HC
AK EA
⇒=
0,5
Từ (1) và (2) suy ra
( )
.
5
DM DH DH AB
DM
AB AK AK
=⇒=
Từ (3) và (4) suy ra
( )
..
6
NC HC HC AB HD AB
NC
AB AK AK AK
= ⇒= =
0,5
Từ (5) và (6) suy ra
.DM NC
=
Vì
BD BC=
nên tam giác
BCD
cân tại
,B
suy ra
.BDM BCN=
Suy ra
.BDM BCN DBF EBC∆ =∆⇒ =
0,5
9
Một cửa hàng bán bưởi Đoan Hùng với giá bán mỗi quả là 50000 đồng. Với giá bán này
thì mỗi ngày cửa hàng chỉ bán được 40 quả. Cửa hàng dự định giảm giá bán, ước tính nếu
cửa hàng cứ giảm mỗi quả 1000 đồng thì số bưởi bán tăng thêm được là 10 quả mỗi ngày.
Xác định giá bán để cửa hàng thu được lợi nhuận cao nhất, biết rằng giá nhập về ban đầu
cho mỗi quả bưởi là 30000 đồng.
2,0
Gọi
x
là giá bán thực tế để có lợi nhuận (
x
: đồng,
30000 50000x≤≤
).
0,5
N
E
M
F
H
D
C
B
A
K