B. Đề kiểm tra giữa học kì 1 ĐỀ SỐ 4
I. Trắc nghiệm (7 điểm)
Câu 1. Cho góc lượng giác 45 . Khẳng định nào sau đây là sai? 2 A. sin . B. sin cos. C. tan 1 . D. cot 1. 2
Câu 2. Một cung của đường tròn bán kính R và có số đo rad thì có độ dài là 1 A. l R. B. 2 l R . C. 2
l R .
D. l R. 2
Câu 3. Chọn khẳng định đúng. 1
A. sin x cos y
sinx y sinx y . 2 1
B. sin x cos y sin x y sin x y . 2 1
C. sin x cos y
sinx y sinx y . 2 1
D. sin x cos y
sinx y sinx y . 2
Câu 4. Giả sử các đẳng thức đều có nghĩa. Đẳng thức sai trong các đẳng thức sau là 2 A. 2 tan a 1 tan a sin 2a . B. cos 2a . 2 1 tan a 2 1 tan a 2 C. 2 tan a 1 tan a tan 2a . D. cot 2a . 2 1 tan a 2 tan a
Câu 5. Mệnh đề nào dưới đây là sai?
A. Đồ thị của một hàm số chẵn nhận trục tung là trục đối xứng.
B. Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
C. Các hàm số y sin x và y cos x tuần hoàn với chu kì 2 .
D. Các hàm số y tan x và y cot x tuần hoàn với chu kì . 2 1
Câu 6. Tập xác định của hàm số là 2 cos x 1
A. D
\ k ,k . B. D
\ k ,k . 2 C. D
\ k2 ,k . D. D
\ k ,k . 2 2
Câu 7. Trong các hàm số sau, hàm số nào là hàm số chẵn? A. y sin . x B. y cos . x C. y tan . x D. y cot . x x
Câu 8. Phương trình 2 0 x
tương đương với phương trình nào trong các phương 2 trình dưới đây. A. 2 x 4 0 .
B. 2x 4 0. 3x 6 C. 0 x . x . D. 4 8 0 2
Câu 9. Khẳng định nào sau đây là đúng?
u v k2
A. sin u sin v k .
u v k2
u v k2
B. sin u sin v k .
u v k2
u v k
C. sin u sin v k .
u v k
u v k
D. sin u sin v k .
u v k 2 Câu 10. x
là nghiệm của phương trình nào sau đây? 3 1 3
A. sin x . B. cot x . 2 3 1
C. tan x 3 . D. cos x . 2 1
Câu 11. Cho dãy số u với u
. Khẳng định nào sau đây là sai? n n n 2
1 1 1 1
A. 5 số hạng đầu của dãy số u là 1 ; ; ; ; . n 2 3 4 5
B. Dãy số u bị chặn trên bởi số M 1 . n
C. Dãy số u bị chặn trên bởi số M 0 . n
D. Dãy số u bị chặn dưới bởi số m 1 . n
Câu 12. Cho dãy số có các số hạng là 8, 13, 18, 23, 28, .... Số hạng tổng quát của dãy số này là
A. u 5n 3 .
B. u 5n 2 .
C. u 5n 3.
D. u 5n 1. n n n n
Câu 13. Dãy số này dưới đây là một cấp số cộng? A. 1; 4; 7; 13; 16. B. 2; 4; 6; 8; 12.
C. 0,1; 0,01; 0,001; 0,0001. D. 3; 5; 7; 9; 11.
Câu 14. Cho cấp số cộng u có u 5 và d 2. Mệnh đề nào sau đây đúng? n 1
A. u 34.
B. u 45.
C. u 27. D. u 35. 13 13 13 13
Câu 15. Trong các dãy số cho bởi công thức truy hồi sau, hãy chọn dãy số là cấp số nhân. u 2 u 1 A. 1 . B. 1 . 2 u u u 3u n 1 n n 1 n u 3 u 3 C. 1 . D. 1 . u u 1 u 2 .nu n 1 n n 1 n 1
Câu 16. Cho cấp số nhân u với u và u 3. Công bội q của cấp số nhân đó n 1 3 2 là A. 2 . B. 2 . C. 9 . D. 9 .
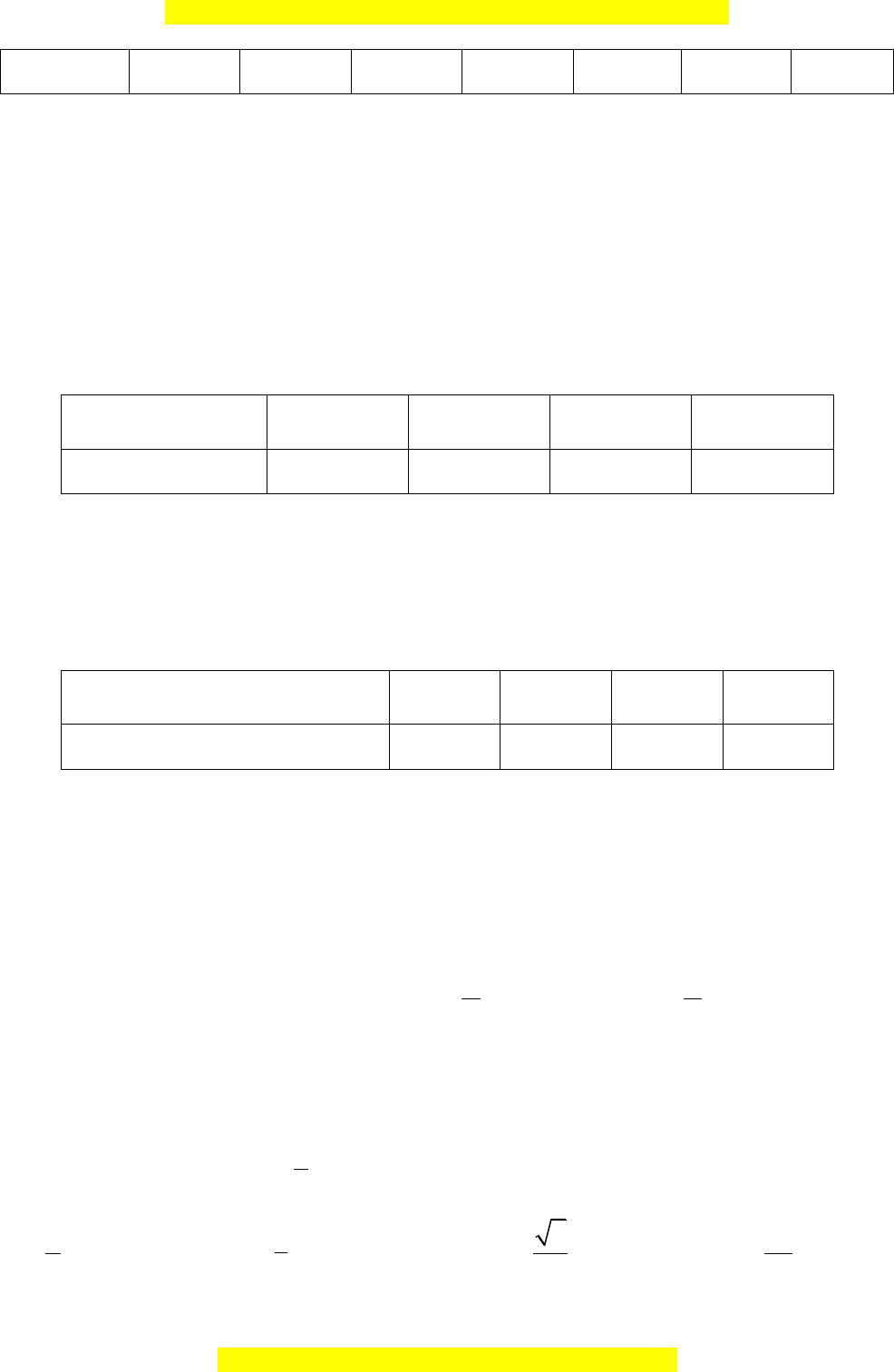
Câu 17. Cho mẫu số liệu ghép nhóm sau: Nhóm
50;52 52;54 54;56 56;58 58;60 60;62 62;68 3
Tần số 5 10 45 20 16 3 1
Mệnh đề đúng là
A. Giá trị 54 thuộc vào nhóm 52;54 .
B. Tần số của nhóm 58;60 là 3.
C. Tần số của nhóm 54;56 là 45.
D. Giá trị 45 thuộc vào nhóm 54;56 .
Câu 18. Mẫu số liệu sau đây cho biết cân nặng của một số con gấu trúc vừa chào đời. Cân nặng (gam)
150;200 200;250 250;300 350;400 Tần số 1 3 5 1
Mẫu số liệu trên có bao nhiêu nhóm? A. 1. B. 3. C. 4. D. 5.
Câu 19. Khảo sát thời gian tự học ở nhà của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
Thời gian tự học ở nhà (giờ) 1;2 2;3 3;4 4;5 Số học sinh 10 30 7 3
Nhóm chứa mốt của mẫu số liệu trên là A. 1;2. B. 2;3 . C. 3;4 . D. 4;5 .
Câu 20. Nhóm chứa trung vị trong mẫu số liệu ở Câu 19 là A. 1;2. B. 2;3 . C. 3;4 . D. 4;5 .
Câu 21. Rút gọn biểu thức A sin sin cos cos ta được kết 2 2 quả là
A. A 4.
B. A 2.
C. A 0. D. A 1. 1
Câu 22. Nếu sinx cos x thì sin 2x bằng 2 3 3 2 3 A. . B. . C. . D. . 4 8 2 4 4
Đề thi giữa kì 1 Toán 11 Kết nối tri thức (đề 4)
0.9 K
461 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ 10 đề giữa kì 1 gồm đầy đủ ma trận và lời giải chi tiết môn Toán 11 bộ Kết nối tri thức mới nhất năm 2023 - 2024 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 11.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(921 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 11
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
1
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
B. Đề kiểm tra giữa học kì 1
ĐỀ SỐ 4
I. Trắc nghiệm (7 điểm)
Câu 1. Cho góc lượng giác
45
. Khẳng định nào sau đây là sai?
A.
2
sin .
2
B.
sin cos .
C.
tan 1.
D.
cot 1.
Câu 2. Một cung của đường tròn bán kính
R
và có số đo
rad thì có độ dài là
A.
1
.
2
lR
B.
2
.lR
C.
2
.lR
D.
.lR
Câu 3. Chọn khẳng định đúng.
A.
1
sin cos sin sin
2
x y x y x y
.
B.
1
sin cos sin sin
2
x y x y x y
.
C.
1
sin cos sin sin
2
x y x y x y
.
D.
1
sin cos sin sin
2
x y x y x y
.
Câu 4. Giả sử các đẳng thức đều có nghĩa. Đẳng thức sai trong các đẳng thức sau là
A.
2
2tan
sin2
1 tan
a
a
a
. B.
2
2
1 tan
cos2
1 tan
a
a
a
.
C.
2
2tan
tan2
1 tan
a
a
a
. D.
2
1 tan
cot2
2tan
a
a
a
.
Câu 5. Mệnh đề nào dưới đây là sai?
A. Đồ thị của một hàm số chẵn nhận trục tung là trục đối xứng.
B. Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
C. Các hàm số
sinyx
và
cosyx
tuần hoàn với chu kì
2.
D. Các hàm số
tanyx
và
cotyx
tuần hoàn với chu kì
.
2
Câu 6. Tập xác định của hàm số
2
1
cos x
là

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
2
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
\,
2
D k k
. B.
\,D k k
.
C.
\ 2 ,
2
D k k
. D.
\,
2
D k k
.
Câu 7. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Câu 8. Phương trình
2
0
2
x
x
tương đương với phương trình nào trong các phương
trình dưới đây.
A.
2
40x
. B.
2 4 0x
.
C.
36
0
2
x
x
. D.
4 8 0x
.
Câu 9. Khẳng định nào sau đây là đúng?
A.
2
sin sin
2
u v k
u v k
u v k
.
B.
2
sin sin
2
u v k
u v k
u v k
.
C.
sin sin
u v k
u v k
u v k
.
D.
sin sin
u v k
u v k
u v k
.
Câu 10.
2
3
x
là nghiệm của phương trình nào sau đây?
A.
1
sin
2
x
. B.
3
cot
3
x
.
C.
tan 3x
. D.
1
cos
2
x
.
Câu 11. Cho dãy số
n
u
với
1
n
u
n
. Khẳng định nào sau đây là sai?

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
3
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. 5 số hạng đầu của dãy số
n
u
là
1111
1; ; ; ;
2 3 4 5
.
B. Dãy số
n
u
bị chặn trên bởi số
1M
.
C. Dãy số
n
u
bị chặn trên bởi số
0M
.
D. Dãy số
n
u
bị chặn dưới bởi số
1m
.
Câu 12. Cho dãy số có các số hạng là 8, 13, 18, 23, 28, .... Số hạng tổng quát của dãy
số này là
A.
53
n
un
. B.
52
n
un
. C.
53
n
un
. D.
51
n
un
.
Câu 13. Dãy số này dưới đây là một cấp số cộng?
A. 1; 4; 7; 13; 16.
B. 2; 4; 6; 8; 12.
C. 0,1; 0,01; 0,001; 0,0001.
D. 3; 5; 7; 9; 11.
Câu 14. Cho cấp số cộng
n
u
có
1
5u
và
2.d
Mệnh đề nào sau đây đúng?
A.
13
34.u
B.
13
45.u
C.
13
27.u
D.
13
35.u
Câu 15. Trong các dãy số cho bởi công thức truy hồi sau, hãy chọn dãy số là cấp số
nhân.
A.
1
2
1
2
nn
u
uu
. B.
1
1
1
3
nn
u
uu
.
C.
1
1
3
1
nn
u
uu
. D.
1
1
3
2.
n
nn
u
uu
.
Câu 16. Cho cấp số nhân
n
u
với
1
1
3
u
và
2
3u
. Công bội
q
của cấp số nhân đó
là
A.
2
. B.
2
. C.
9
. D.
9
.
Câu 17. Cho mẫu số liệu ghép nhóm sau:
Nhóm
50;52
52;54
54;56
56;58
58;60
60;62
62;68
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
4
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Tần số
5
10
45
20
16
3
1
Mệnh đề đúng là
A. Giá trị 54 thuộc vào nhóm
52;54
.
B. Tần số của nhóm
58;60
là 3.
C. Tần số của nhóm
54;56
là 45.
D. Giá trị 45 thuộc vào nhóm
54;56
.
Câu 18. Mẫu số liệu sau đây cho biết cân nặng của một số con gấu trúc vừa chào đời.
Cân nặng (gam)
150;200
200;250
250;300
350;400
Tần số
1
3
5
1
Mẫu số liệu trên có bao nhiêu nhóm?
A. 1. B. 3. C. 4. D. 5.
Câu 19. Khảo sát thời gian tự học ở nhà của một số học sinh khối 11 thu được mẫu
số liệu ghép nhóm sau:
Thời gian tự học ở nhà (giờ)
1;2
2;3
3;4
4;5
Số học sinh
10
30
7
3
Nhóm chứa mốt của mẫu số liệu trên là
A.
1;2
. B.
2;3
. C.
3;4
. D.
4;5
.
Câu 20. Nhóm chứa trung vị trong mẫu số liệu ở Câu 19 là
A.
1;2
. B.
2;3
. C.
3;4
. D.
4;5
.
Câu 21. Rút gọn biểu thức
sin sin cos cos
22
A
ta được kết
quả là
A.
4.A
B.
2.A
C.
0.A
D.
1.A
Câu 22. Nếu
1
sin cos
2
xx
thì
sin2x
bằng
A.
3
4
. B.
3
8
. C.
2
2
. D.
3
4
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
5
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 23. Thu gọn biểu thức
1 cos cos2 cos3
cos cos2
x x x
P
xx
ta được kết quả là
.cosa bx
,
,ab
. Khi đó
T a b
có kết quả là
A.
0T
. B.
1T
. C.
1T
. D.
3T
.
Câu 24. Trong các hàm số cho dưới đây, hàm số nào là hàm số chẵn?
A.
tanyx
. B.
2
tany x x
. C.
siny x x
. D.
cosy x x
.
Câu 25. Tập giá trị của hàm số
2
sin 2 1f x x
là
A.
1;1
. B.
0;1
. C.
1;0
. D.
1;2
.
Câu 26. Tất cả nghiệm của phương trình
cos 3 cos
48
x
là
A.
2
,
24 3
x k k
.
B.
2
,
24 3
x k k
.
C.
2
8
xk
và
3
2,
8
x k k
.
D.
2
24 3
xk
và
2
,
83
x k k
.
Câu 27. Tại các giá trị nào của
x
thì đồ thị hàm số
cosyx
và
sinyx
giao nhau?
A.
2,
4
x k k
. B.
2,
2
x k k
.
C.
,
4
x k k
. D.
,
4
x k k
.
Câu 28. Trong các dãy số sau, dãy số nào không là dãy số bị chặn?
A.
n
a
với
21
n
n
a
n
. B.
n
u
với
cos
n
un
.
C.
:1,2,3,4,5,6,7
n
b
. D.
n
v
với
n
vn
.
Câu 29. Cho dãy số
n
u
với
n
na
u
n
,
a
là số thực. Tìm một giá trị của
a
để
n
u
là dãy số tăng.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
6
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
1
2
a
. B.
1a
. C.
0a
. D.
1a
.
Câu 30. Một cấp số cộng có
6
số hạng. Biết rằng tổng của số hạng đầu và số hạng
cuối bằng 17; tổng của số hạng thứ hai và số hạng thứ tư bằng 14. Tìm công sai
d
của cấp số cộng đã cho.
A.
2.d
B.
3.d
C.
4.d
D.
5.d
Câu 31. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan
giếng nước đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80 000
đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5 000 đồng so với giá
của mét khoan trước đó. Biết cần phải khoan sâu xuống 50 m mới có nước. Vậy hỏi
phải trả bao nhiêu tiền để khoan cái giếng đó?
A.
5.250.000
đồng. B.
10.125.000
đồng.
C.
4.000.000
đồng. D.
4.245.000
đồng.
Câu 32. Tổng 7 số hạng đầu cấp số nhân
n
u
với
1
3u
và công bội
1
2
q
là
A.
381
64
. B.
189
32
. C.
63
32
. D.
889
64
.
Câu 33. Cho cấp số nhân
n
u
có
4
1
32
u
và
5
1
.
128
u
Khi đó, số hạng đầu
1
u
và
công bội
q
là bao nhiêu ?
A.
1
3, 5uq
. B.
1
1
2,
4
uq
.
C.
1
1
2,
2
uq
. D.
1
1
2,
4
uq
.
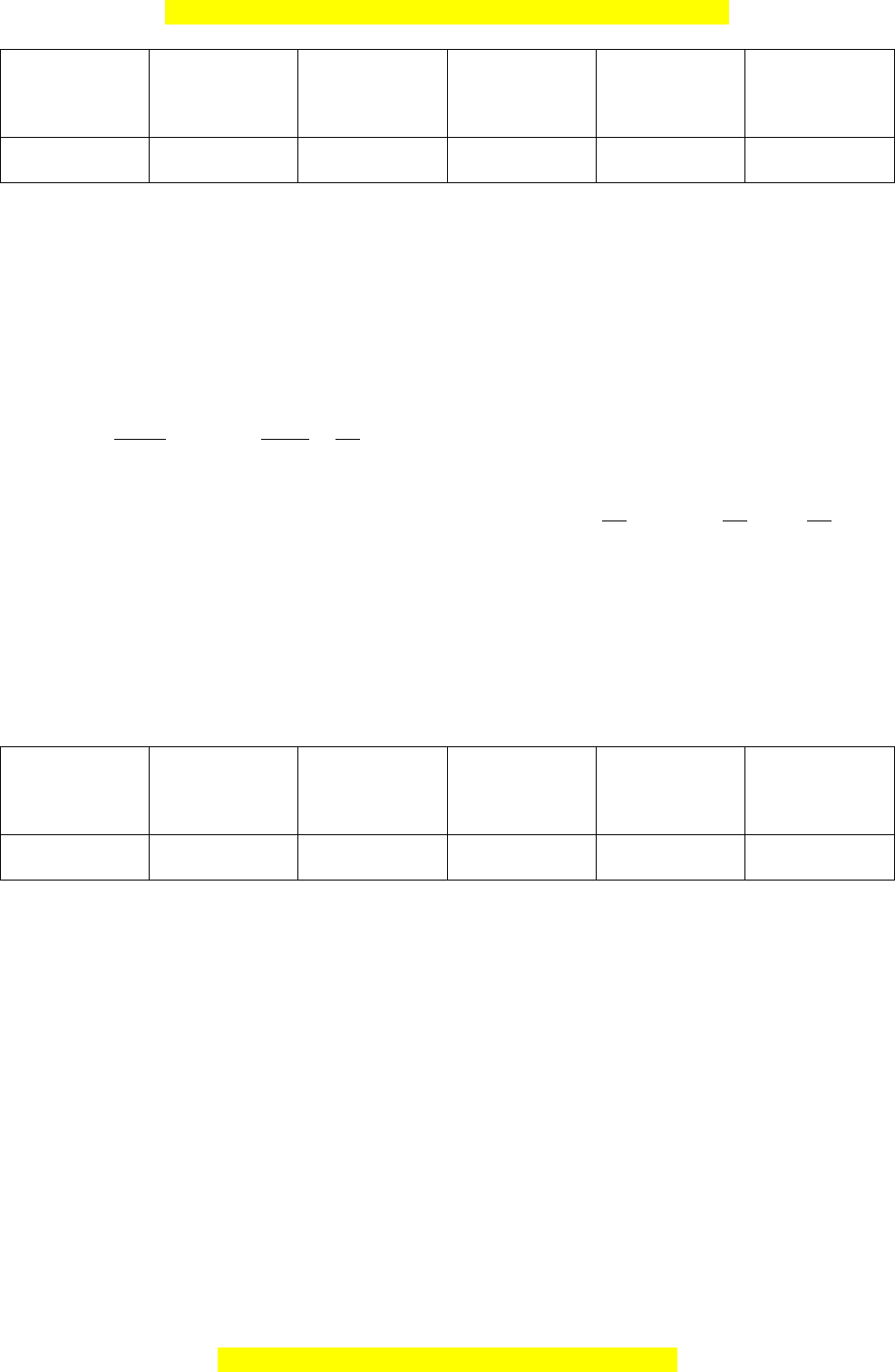
Câu 34. Cho mẫu số liệu ghép nhóm về chiều cao của 50 cây mít giống như sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là
A.
1
13,5Q
. B.
1
13,9Q
. C.
1
15,75Q
. D.
1
13,75Q
.
Câu 35. Người ta ghi lại tuổi thọ của một số con ruồi giấm cho kết quả như sau:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
7
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Tuổi thọ
(ngày)
40;42
42;44
44;46
46;48
48;50
Số lượng
5
12
23
31
29
Tuổi thọ trung bình của ruồi giấm trong mẫu số liệu trên là
A.
46,64
. B.
46,34
. C.
43,64
. D.
43,46
.
II. Tự luận (3 điểm)
Bài 1. (1 điểm) Giải các phương trình:
a)
cos cos5 cos2 cos4x x x x
;
b)
1 1 10
cos sin
cos sin 3
xx
xx
.
Bài 2. (1 điểm) Tìm tất cả các số thực
x
sao cho
tan ,tan ,tan
12 12 12
xx
tạo thành một cấp số nhân theo thứ tự nào đó.
Bài 3. (1 điểm) Để kiểm tra thời gian sử dụng pin của chiếc đèn tích điện mới, chị
Nga thống kê thời gian sử dụng đèn của mình từ lúc sạc đầy pin cho đến khi hết pin ở
bảng sau:
Thời gian sử
dụng (giờ)
7;9
9;11
11;13
13;15
15;17
Số lần
2
5
7
6
3
a) Hãy ước lượng thời gian sử dụng trung bình từ lúc chị Nga sạc đầy pin đèn cho tới
khi hết pin.
b) Chị Nga cho rằng có khoảng 25% số lần sạc pin đèn chỉ dùng được dưới 10 giờ.
Nhận định của chị Nga có hợp lí không?
-----HẾT-----
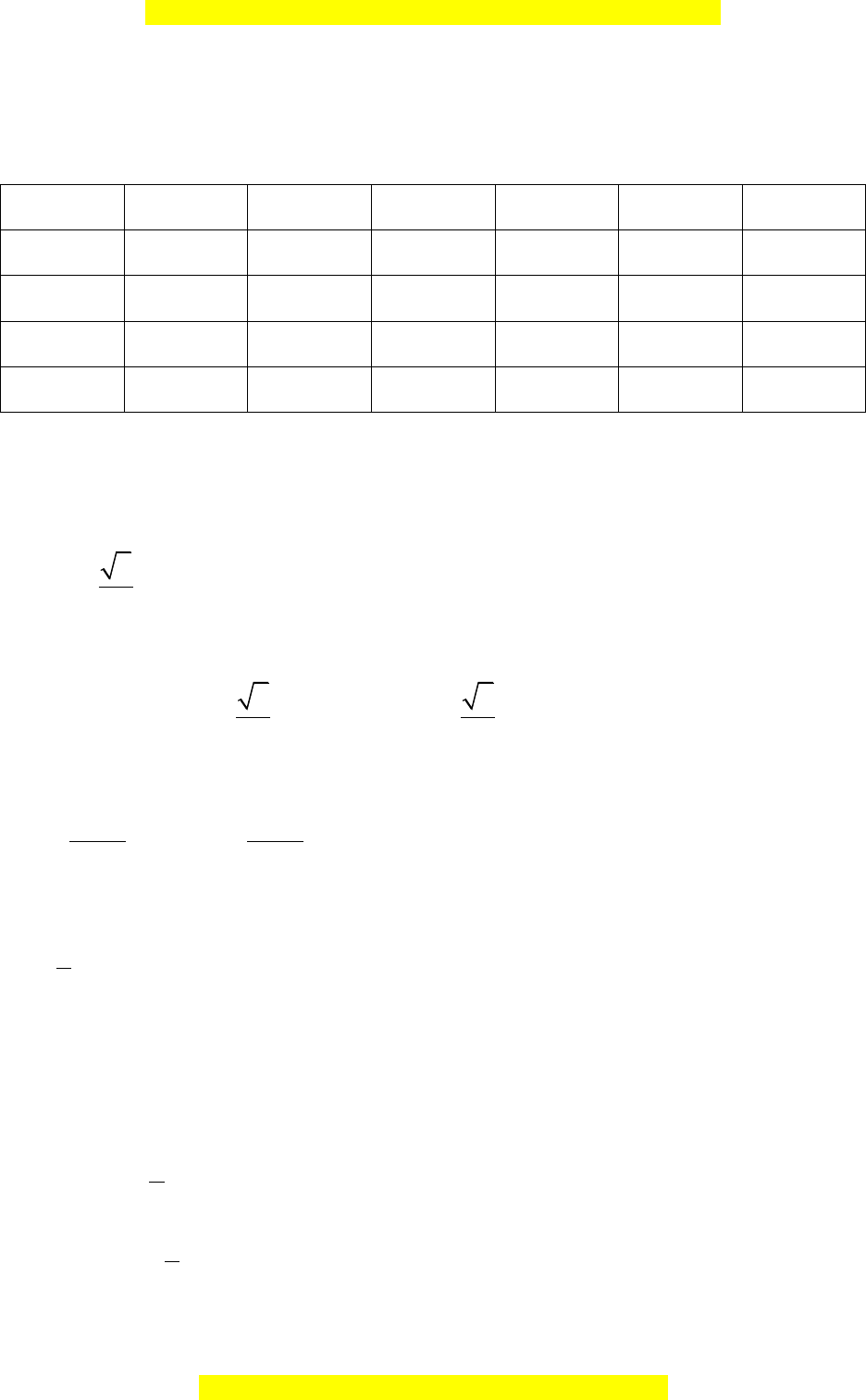
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
8
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C. Đáp án và hướng dẫn giải đề kiểm tra giữa học kì 1
ĐÁP ÁN ĐỀ SỐ 4
I. Bảng đáp án trắc nghiệm
1. C
2. C
3. A
4. A
5. D
6. A
7. B
8. B
9. A
10. D
11. B
12. C
13. D
14. C
15. B
16. D
17. C
18. C
19. B
20. B
21. C
22. D
23. B
24. C
25. D
26. D
27. D
28. D
29. D
30. B
31. B
32. A
33. D
34. D
35. B
II. Hướng dẫn giải chi tiết trắc nghiệm
Câu 1. Cho góc lượng giác
45
. Khẳng định nào sau đây là sai?
A.
2
sin .
2
B.
sin cos .
C.
tan 1.
D.
cot 1.
Đáp án đúng là: C
Ta có:
22
sin sin45 ;cos cos45
22
nên
sin cos .
Vậy đáp án A, B
đúng.
sin cos
tan 1;cot 1
cos sin
. Vậy đáp án D đúng, đáp án C sai.
Câu 2. Một cung của đường tròn bán kính
R
và có số đo
rad thì có độ dài là
A.
1
.
2
lR
B.
2
.lR
C.
2
.lR
D.
.lR
Đáp án đúng là: C
Một cung của đường tròn bán kính
R
và có số đo
rad thì có độ dài là
.lR
Câu 3. Chọn khẳng định đúng.
A.
1
sin cos sin sin
2
x y x y x y
.
B.
1
sin cos sin sin
2
x y x y x y
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
9
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C.
1
sin cos sin sin
2
x y x y x y
.
D.
1
sin cos sin sin
2
x y x y x y
.
Đáp án đúng là: A
Chọn A vì đúng theo công thức biến đổi tích thành tổng.
Câu 4. Giả sử các đẳng thức đều có nghĩa. Đẳng thức sai trong các đẳng thức sau là
A.
2
2tan
sin2
1 tan
a
a
a
. B.
2
2
1 tan
cos2
1 tan
a
a
a
.
C.
2
2tan
tan2
1 tan
a
a
a
. D.
2
1 tan
cot2
2tan
a
a
a
.
Đáp án đúng là: A
Theo công thức nhân đôi, ta có
2
2tan
tan2
1 tan
a
a
a
, từ đó suy ra
2
1 tan
cot2
2tan
a
a
a
,
nên đáp án C và D đúng.
Ta có:
2
2
2
2
1
11
1 tan
cos
1
1 tan
cos
a
a
a
a
22
2
1
2 .cos 2cos 1
cos
aa
a
cos2a
, nên
đáp án B đúng. Vậy đáp án A sai.
Câu 5. Mệnh đề nào dưới đây là sai?
A. Đồ thị của một hàm số chẵn nhận trục tung là trục đối xứng.
B. Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.
C. Các hàm số
sinyx
và
cosyx
tuần hoàn với chu kì
2.
D. Các hàm số
tanyx
và
cotyx
tuần hoàn với chu kì
.
2
Đáp án đúng là: D
Các đáp án A, B, C đúng theo lý thuyết.
Các hàm số
tanyx
và
cotyx
tuần hoàn với chu kì
.
Vậy đáp án D sai.
Câu 6. Tập xác định của hàm số
2
1
cos x
là

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
10
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
\,
2
D k k
. B.
\,D k k
.
C.
\ 2 ,
2
D k k
. D.
\,
2
D k k
.
Đáp án đúng là: A
Hàm số
2
1
cos x
xác định khi
2
cos 0 cos 0 ,
2
x x x k k
.
Vậy tập xác định của hàm số
2
1
cos x
là
\,
2
D k k
.
Câu 7. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
sin .yx
B.
cos .yx
C.
tan .yx
D.
cot .yx
Đáp án đúng là: B
Nhắc lại kiến thức cơ bản:
- Hàm số
sinyx
là hàm số lẻ.
- Hàm số
cosyx
là hàm số chẵn.
- Hàm số
tanyx
là hàm số lẻ.
- Hàm số
cotyx
là hàm số lẻ.
Vậy B là đáp án đúng.
Câu 8. Phương trình
2
0
2
x
x
tương đương với phương trình nào trong các phương
trình dưới đây.
A.
2
40x
. B.
2 4 0x
.
C.
36
0
2
x
x
. D.
4 8 0x
.
Đáp án đúng là: B
Phương trình
2
0
2
x
x
có tập nghiệm là
1
2S
.
Phương trình
2 4 0x
có tập nghiệm là
2
2S
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
11
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vì
12
SS
nên hai phương trình
2
0
2
x
x
và
2 4 0x
tương đương.
Câu 9. Khẳng định nào sau đây là đúng?
A.
2
sin sin
2
u v k
u v k
u v k
.
B.
2
sin sin
2
u v k
u v k
u v k
.
C.
sin sin
u v k
u v k
u v k
.
D.
sin sin
u v k
u v k
u v k
.
Đáp án đúng là: A
Theo lí thuyết ta có
2
sin sin
2
u v k
u v k
u v k
.
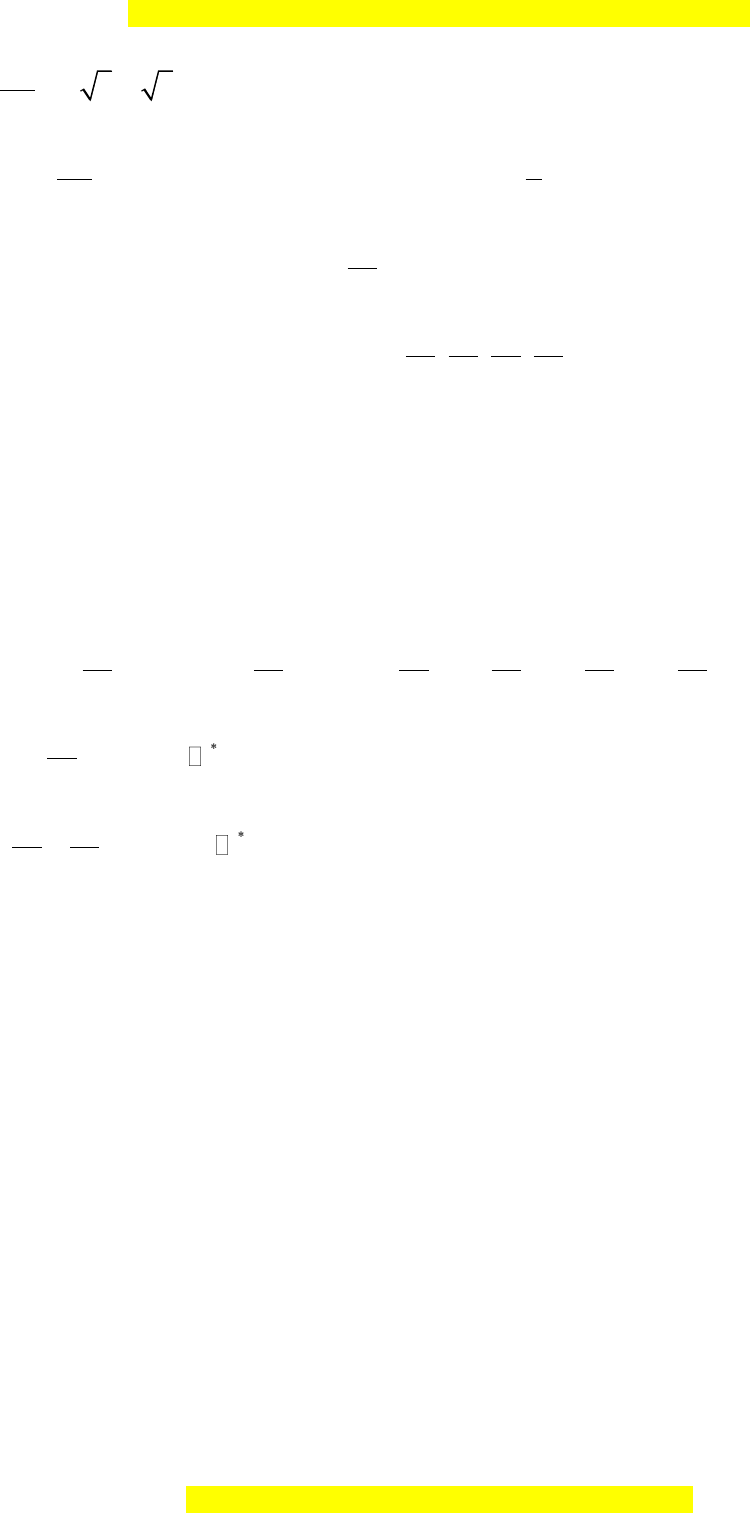
Câu 10.
2
3
x
là nghiệm của phương trình nào sau đây?
A.
1
sin
2
x
. B.
3
cot
3
x
.
C.
tan 3x
. D.
1
cos
2
x
.
Đáp án đúng là: D
Thay
2
3
x
vào các phương trình đã cho, ta thấy:
2 3 1
sin
3 2 2
21
cos
32
2 3 3
cot
3 3 3
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
12
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
2
tan 3 3
3
Vậy
2
3
x
là nghiệm của phương trình
1
cos
2
x
.
Câu 11. Cho dãy số
n
u
với
1
n
u
n
. Khẳng định nào sau đây là sai?
A. 5 số hạng đầu của dãy số
n
u
là
1111
1; ; ; ;
2 3 4 5
.
B. Dãy số
n
u
bị chặn trên bởi số
1M
.
C. Dãy số
n
u
bị chặn trên bởi số
0M
.
D. Dãy số
n
u
bị chặn dưới bởi số
1m
.
Đáp án đúng là: B
Ta có
1
n
u
n
, do đó
1 2 3 4 5
1 1 1 1 1
1, , , ,
1 2 3 4 5
u u u u u
.
Vì
*
1
0
n
un
n
nên dãy số
n
u
bị chặn trên bởi số
0M
.
*
11
1
1
n
un
n
nên dãy số
n
u
bị chặn dưới bởi số
1m
.
Câu 12. Cho dãy số có các số hạng là 8, 13, 18, 23, 28, .... Số hạng tổng quát của dãy
số này là
A.
53
n
un
. B.
52
n
un
. C.
53
n
un
. D.
51
n
un
.
Đáp án đúng là: C
Xét từng đáp án:
- Đáp án A ta có:
1
5.1 3 2 8u
, không thỏa mãn.
- Đáp án B ta có:
1
5.1 2 7 8u
, không thỏa mãn.
- Đáp án C ta có:
1
5.1 3 8u
, thỏa mãn.
- Đáp án D ta có:
1
5.1 1 4 8u
, không thỏa mãn.
Câu 13. Dãy số này dưới đây là một cấp số cộng?
A. 1; 4; 7; 13; 16.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
13
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
B. 2; 4; 6; 8; 12.
C. 0,1; 0,01; 0,001; 0,0001.
D. 3; 5; 7; 9; 11.
Đáp án đúng là: D
Dãy số 3; 5; 7; 9; 11 là một cấp số cộng.
Câu 14. Cho cấp số cộng
n
u
có
1
5u
và
2.d
Mệnh đề nào sau đây đúng?
A.
13
34.u
B.
13
45.u
C.
13
27.u
D.
13
35.u
Đáp án đúng là: C
Ta có
1
13 1
5
13 1 5 13 1 .2 27
2
CTTQ
u
u u d
d
.
Câu 15. Trong các dãy số cho bởi công thức truy hồi sau, hãy chọn dãy số là cấp số
nhân.
A.
1
2
1
2
nn
u
uu
. B.
1
1
1
3
nn
u
uu
.
C.
1
1
3
1
nn
u
uu
. D.
1
1
3
2.
n
nn
u
uu
.
Đáp án đúng là: B
Xét
1
1
1
3
nn
u
uu
. Ta có
1
3
3
nn
nn
uu
uu
không đổi với mọi
*
n
.
Vậy dãy số trên là cấp số nhân.
Câu 16. Cho cấp số nhân
n
u
với
1
1
3
u
và
2
3u
. Công bội
q
của cấp số nhân đó
là
A.
2
. B.
2
. C.
9
. D.
9
.
Đáp án đúng là: D
Vì
n
u
là cấp số nhân nên công bội
2
1
3
9
1
3
u
q
u
.
Câu 17. Cho mẫu số liệu ghép nhóm sau:

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
14
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Nhóm
50;52
52;54
54;56
56;58
58;60
60;62
62;68
Tần số
5
10
45
20
16
3
1
Mệnh đề đúng là
A. Giá trị 54 thuộc vào nhóm
52;54
.
B. Tần số của nhóm
58;60
là 3.
C. Tần số của nhóm
54;56
là 45.
D. Giá trị 45 thuộc vào nhóm
54;56
.
Đáp án đúng là: C
Quan sát mẫu số liệu đã cho, ta có:
- Giá trị 54 không thuộc vào nhóm
52;54
.
- Tần số của nhóm
58;60
là 16.
- Tần số của nhóm
54;56
là 45.
- Giá trị 45 không thuộc vào nhóm
54;56
.
Câu 18. Mẫu số liệu sau đây cho biết cân nặng của một số con gấu trúc vừa chào đời.
Cân nặng (gam)
150;200
200;250
250;300
350;400
Tần số
1
3
5
1
Mẫu số liệu trên có bao nhiêu nhóm?
A. 1. B. 3. C. 4. D. 5.
Đáp án đúng là: C
Mẫu số liệu đã cho gồm có 4 nhóm:
150;200
,
200;250
,
250;300
và
350;400
.
Câu 19. Khảo sát thời gian tự học ở nhà của một số học sinh khối 11 thu được mẫu
số liệu ghép nhóm sau:
Thời gian tự học ở nhà (giờ)
1;2
2;3
3;4
4;5
Số học sinh
10
30
7
3
Nhóm chứa mốt của mẫu số liệu trên là
A.
1;2
. B.
2;3
. C.
3;4
. D.
4;5
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
15
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đáp án đúng là: B
Tần số lớn nhất là 30 nên nhóm chứa mốt là nhóm
2;3
.
Câu 20. Nhóm chứa trung vị trong mẫu số liệu ở Câu 19 là
A.
1;2
. B.
2;3
. C.
3;4
. D.
4;5
.
Đáp án đúng là: B
Ta có cỡ mẫu
10 30 7 3 50n
.
Gọi
1 2 50
, ,...,x x x
là thời gian tự học ở nhà của 50 học sinh khối 11 và giả sử dãy này
đã được xếp theo thứ tự không giảm. Khi đó, trung vị là
25 26
2
xx
. Do
25 26
,xx
đều
thuộc nhóm
2;3
nên nhóm này chứa trung vị của mẫu số liệu.
Câu 21. Rút gọn biểu thức
sin sin cos cos
22
A
ta được kết
quả là
A.
4.A
B.
2.A
C.
0.A
D.
1.A
Đáp án đúng là: C
Ta có
sin sin cos cos
22
;
cos cos sin sin
22
.
Khi đó
sin sin cos cos
22
A
sin cos cos sin 0
.
Câu 22. Nếu
1
sin cos
2
xx
thì
sin2x
bằng
A.
3
4
. B.
3
8
. C.
2
2
. D.
3
4
.
Đáp án đúng là: D
Ta có
1
sin cos
2
xx
22
1
sin 2sin cos cos
4
x x x x
3
sin2
4
x
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
16
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 23. Thu gọn biểu thức
1 cos cos2 cos3
cos cos2
x x x
P
xx
ta được kết quả là
.cosa bx
,
,ab
. Khi đó
T a b
có kết quả là
A.
0T
. B.
1T
. C.
1T
. D.
3T
.
Đáp án đúng là: B
Ta có:
23
2
1 cos cos2 cos3 1 cos 2cos 1 4cos 3cos
cos cos2 cos 2cos 1
x x x x x x x
P
x x x x
2
32
22
2cos 2cos cos 1
4cos 2cos 2cos
2cos
2cos cos 1 2cos cos 1
x x x
x x x
x
x x x x
.
Khi đó
2, 1ab
, vậy
2 1 1T a b
.
Câu 24. Trong các hàm số cho dưới đây, hàm số nào là hàm số chẵn?
A.
tanyx
. B.
2
tany x x
. C.
siny x x
. D.
cosy x x
.
Đáp án đúng là: C
Xét hàm số
sinf x x x
Tập xác định:
D
Với mọi
x D x D
Ta có
sin sinf x x x x x f x
sinf x x x
là hàm số chẵn.
Câu 25. Tập giá trị của hàm số
2
sin 2 1f x x
là
A.
1;1
. B.
0;1
. C.
1;0
. D.
1;2
.
Đáp án đúng là: D
Vì
22
0 sin 2 1 1 sin 2 1 2 1 2x x f x
Vậy tập giá trị của hàm số
2
sin 2 1f x x
là
1;2
.
Câu 26. Tất cả nghiệm của phương trình
cos 3 cos
48
x
là
A.
2
,
24 3
x k k
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
17
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
B.
2
,
24 3
x k k
.
C.
2
8
xk
và
3
2,
8
x k k
.
D.
2
24 3
xk
và
2
,
83
x k k
.
Đáp án đúng là: D
2
24 3
cos 3 cos 3 2
2
4 8 4 8
83
xk
x x k
xk
với
k
.
Câu 27. Tại các giá trị nào của
x
thì đồ thị hàm số
cosyx
và
sinyx
giao nhau?
A.
2,
4
x k k
. B.
2,
2
x k k
.
C.
,
4
x k k
. D.
,
4
x k k
.
Đáp án đúng là: D
2
2
cos sin cos cos ,
24
2
2
x x k
x x x x x k k
x x k
.
Câu 28. Trong các dãy số sau, dãy số nào không là dãy số bị chặn?
A.
n
a
với
21
n
n
a
n
. B.
n
u
với
cos
n
un
.
C.
:1,2,3,4,5,6,7
n
b
. D.
n
v
với
n
vn
.
Đáp án đúng là: D
Ta có:
*
2 3,
n
an
. Suy ra dãy số
n
a
là dãy số bị chặn.
*
1 1,
n
un
. Suy ra dãy số
n
u
là dãy số bị chặn.
1 7, 1;2;3;4;5;6;7
n
bn
. Suy ra dãy số
n
b
là dãy số bị chặn.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
18
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lấy số tự nhiên
N
bất kỳ, tồn tại
1nN
sao cho
1
1
nN
v v N N
. Suy
ra dãy số
n
v
không là dãy số bị chặn trên nên nó không bị chặn.
Câu 29. Cho dãy số
n
u
với
n
na
u
n
,
a
là số thực. Tìm một giá trị của
a
để
n
u
là dãy số tăng.
A.
1
2
a
. B.
1a
. C.
0a
. D.
1a
.
Đáp án đúng là: D
Ta có:
*
1
1
,
11
nn
n a n a a
u u n
n n n n
.
Nếu
0a
thì
*
1
0,
nn
u u n
. Suy ra
n
u
là dãy số giảm.
Nếu
0a
thì
*
1
0,
nn
u u n
. Suy ra
n
u
là dãy số tăng.
Nếu
0a
thì
*
1
,
nn
u u n
. Suy ra
n
u
không là dãy số giảm cũng không là dãy
số tăng.
Vậy để
n
u
là dãy số tăng ta chọn một số
a
sao cho
0a
.
Câu 30. Một cấp số cộng có
6
số hạng. Biết rằng tổng của số hạng đầu và số hạng
cuối bằng 17; tổng của số hạng thứ hai và số hạng thứ tư bằng 14. Tìm công sai
d
của cấp số cộng đã cho.
A.
2.d
B.
3.d
C.
4.d
D.
5.d
Đáp án đúng là: B
Ta có:
16
1
1
1
24
17
2 5 17
1
2 4 14
14
3
uu
ud
u
ud
uu
d
.
Câu 31. Một gia đình cần khoan một cái giếng để lấy nước. Họ thuê một đội khoan
giếng nước đến để khoan giếng nước. Biết giá của mét khoan đầu tiên là 80 000
đồng, kể từ mét khoan thứ 2 giá của mỗi mét khoan tăng thêm 5 000 đồng so với giá
của mét khoan trước đó. Biết cần phải khoan sâu xuống 50 m mới có nước. Vậy hỏi
phải trả bao nhiêu tiền để khoan cái giếng đó?
A.
5.250.000
đồng. B.
10.125.000
đồng.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
19
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C.
4.000.000
đồng. D.
4.245.000
đồng.
Đáp án đúng là: B
Giá tiền khoan mỗi mét (bắt đầu từ mét đầu tiên) lập thành cấp số cộng
n
u
có
1
80000, 5000.ud
Do cần khoan 50 mét nên tổng số tiền cần trả là:
50 502 11
50.49
50 10.125.000
2
uu udu S
.
Câu 32. Tổng 7 số hạng đầu cấp số nhân
n
u
với
1
3u
và công bội
1
2
q
là
A.
381
64
. B.
189
32
. C.
63
32
. D.
889
64
.
Đáp án đúng là: A
Ta có:
7
7
1
3. 1
2
381
1
64
1
2
S
.
Câu 33. Cho cấp số nhân
n
u
có
4
1
32
u
và
5
1
.
128
u
Khi đó, số hạng đầu
1
u
và
công bội
q
là bao nhiêu ?
A.
1
3, 5uq
. B.
1
1
2,
4
uq
.
C.
1
1
2,
2
uq
. D.
1
1
2,
4
uq
.
Đáp án đúng là: D
Ta có:
3
41
. u u q
và
4
51
. u u q
. Chia vế theo vế hai đẳng thức trên, ta được
3
41
4
51
. 1 128 1 1
.
. 32 4
u u q
q
u u q q q
Khi đó,
3
3
4 1 1 1
11
. . 2.
32 4
u u q u u
Vậy cấp số nhân
n
u
có số hạng đầu
1
2u
và
1
.
4
q

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
20
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 34. Cho mẫu số liệu ghép nhóm về chiều cao của 50 cây mít giống như sau:
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm này là
A.
1
13,5Q
. B.
1
13,9Q
. C.
1
15,75Q
. D.
1
13,75Q
.
Đáp án đúng là: D
Cỡ mẫu :
4 6 7 5 3 25n
.
Tứ phân vị thứ nhất
1
Q
là
67
2
xx
. Do
67
,xx
đều thuộc nhóm
10;20
nên nhóm này
chứa
1
Q
.
Do đó:
2p
,
2
10a
,
2
6m
,
1
4m
,
32
10aa
. Ta có:
1
25
4
4
10 .10 13,75
6
Q
.
Câu 35. Người ta ghi lại tuổi thọ của một số con ruồi giấm cho kết quả như sau:
Tuổi thọ
(ngày)
40;42
42;44
44;46
46;48
48;50
Số lượng
5
12
23
31
29
Tuổi thọ trung bình của ruồi giấm trong mẫu số liệu trên là
A.
46,64
. B.
46,34
. C.
43,64
. D.
43,46
.
Đáp án đúng là: B
Cỡ mẫu
5 12 23 31 29 100n
.
Ta có bảng sau:
Giá trị đại
diện tuổi thọ
(ngày)
41
43
45
47
49
Số lượng
5
12
23
31
29
Tuổi thọ trung bình của ruồi giấm trong mẫu số liệu trên là
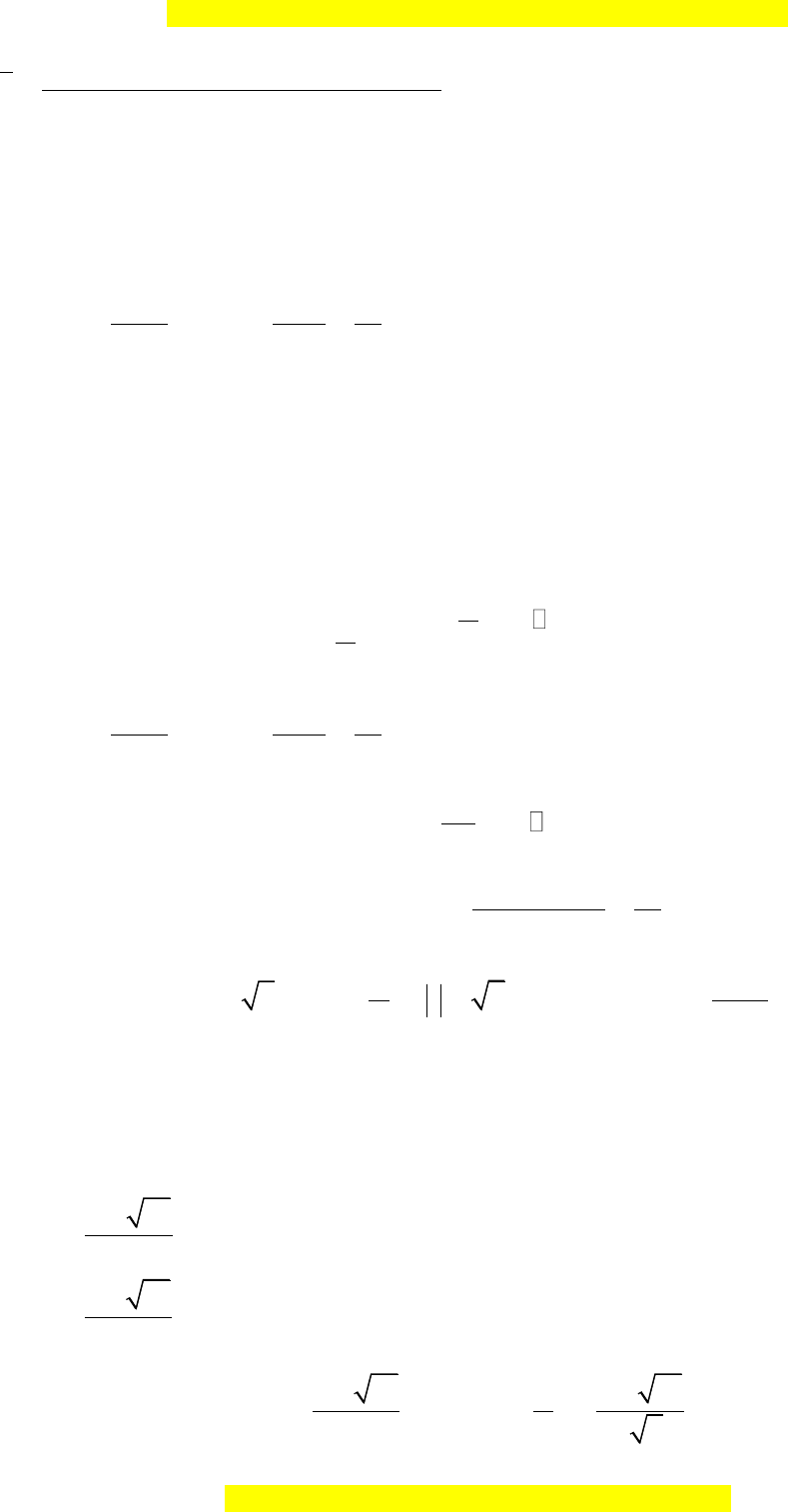
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
21
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
5.41 12.43 23.45 31.47 29.49
46,34
100
x
.
III. Hướng dẫn giải tự luận
Bài 1. (1 điểm) Giải các phương trình:
a)
cos cos5 cos2 cos4x x x x
;
b)
1 1 10
cos sin
cos sin 3
xx
xx
.
Lời giải:
a)
cos cos5 cos2 cos4x x x x
cos6 cos4 cos6 cos2x x x x
cos4 cos2
4 2 2
4 2 2
3
3
xx
xk
x x k
x k k
x x k
xk
b)
1 1 10
cos sin
cos sin 3
xx
xx
Điều kiện
sin 0x
và
cos 0x
2
k
xk
.
Phương trình được biến đổi
sin cos 10
sin cos
sin .cos 3
xx
xx
xx
.
Đặt
sin cos 2sin
4
t x x x
,
2t
. Thì
2
1
sin .cos
2
t
xx
.
Và phương trình trở thành:
3 2 2
3 10 3 10 0 2 3 4 5 0t t t t t t
2
2 19
3
2 19
3
t
t
t
.
Kết hợp điều kiện, chọn
2 19 2 19
sin sin
34
32
tx

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
22
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
2
4
xk
hoặc
2
4
xk
k
2
4
xk
hoặc
3
2
4
xk
k
Vậy nghiệm của phương trình:
2
4
xk
,
3
2
4
x k k
.
Bài 2. (1 điểm) Tìm tất cả các số thực
x
sao cho
tan ,tan ,tan
12 12 12
xx
tạo thành một cấp số nhân theo thứ tự nào đó.
Lời giải:
Đặt
tan
12
a
và
tanyx
. Xét ba trường hợp của 3 thứ tự:
Trường hợp 1:
2
tan .tan tan :
12 12 12
xx
2 2 2 2 2 2
.1
11
a y a y
a a y a a y
ay ay
42
10ay
. Vì
1a
ta có
0y
Do đó
tan 0 ,x x k k
là nghiệm của bài toán.
Trường hợp 2:
2
tan .tan tan
12 12 12
xx
2
2 2 2
1 1 3 0
11
a y a y
a a y ay a y a
ay ay
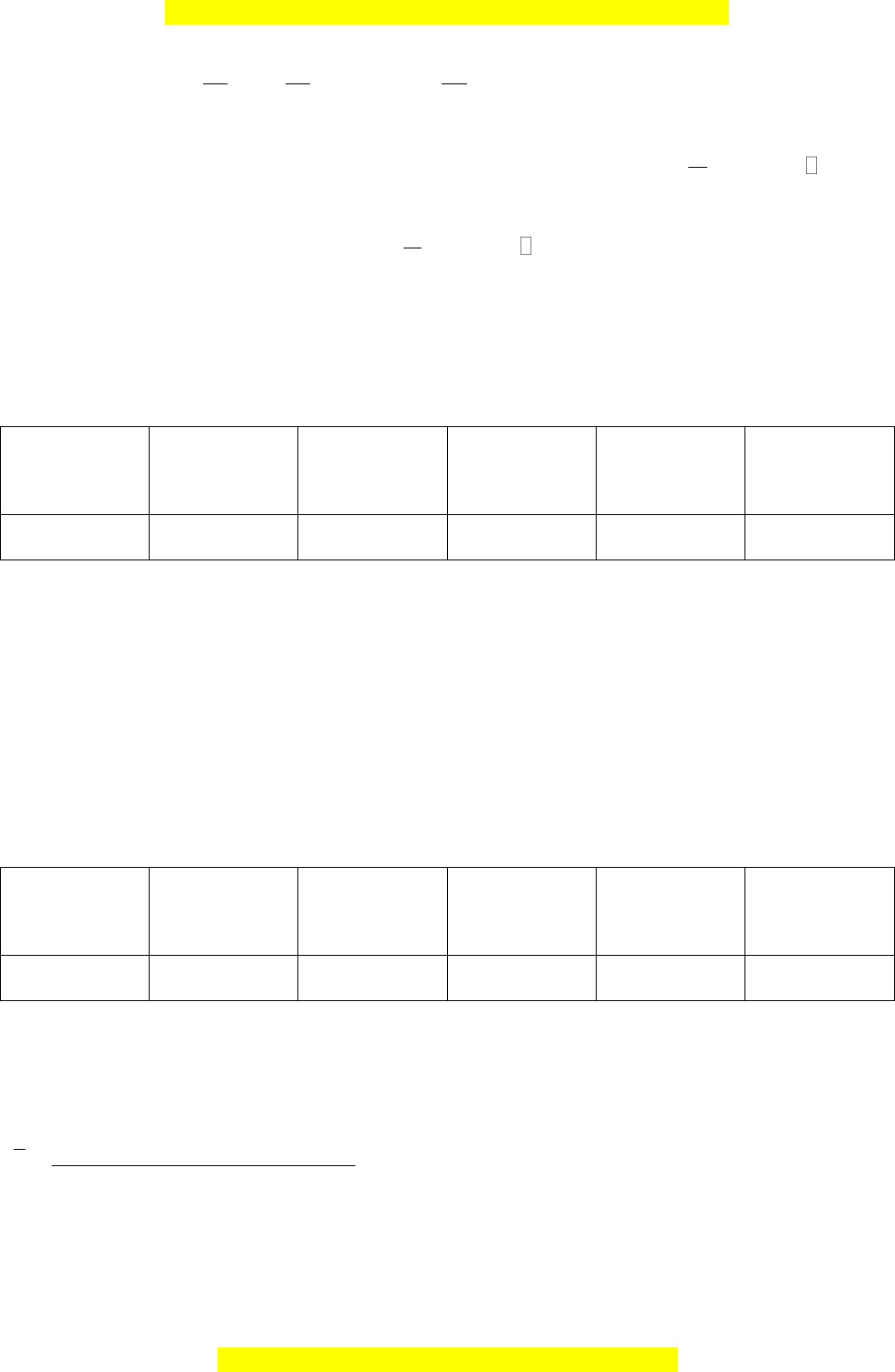
Ta có:
0 , .y x k k
Khi
22
1 3 0ay a y a
vì
tan tan 2 3
12 4 6
a
nên
2
2 3 3 0yy
, suy ra
12
3.yy
Do đó
tan 3 ,
3
x x k k
là nghiệm của bài toán.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
23
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Trường hợp 3:
2
tan .tan tan
12 12 12
xx
Thay
x
bởi
x
, dựa vào kết qyả trên thì nghiệm bài toán là:
,
3
x k k
Vậy các số cần tìm là
xk
và
,
3
x k k
.
Bài 3. (1 điểm) Để kiểm tra thời gian sử dụng pin của chiếc đèn tích điện mới, chị
Nga thống kê thời gian sử dụng đèn của mình từ lúc sạc đầy pin cho đến khi hết pin ở
bảng sau:
Thời gian sử
dụng (giờ)
7;9
9;11
11;13
13;15
15;17
Số lần
2
5
7
6
3
a) Hãy ước lượng thời gian sử dụng trung bình từ lúc chị Nga sạc đầy pin đèn cho tới
khi hết pin.
b) Chị Nga cho rằng có khoảng 25% số lần sạc pin đèn chỉ dùng được dưới 10 giờ.
Nhận định của chị Nga có hợp lí không?
Lời giải:
a) Từ bảng số liệu ghép nhóm, ta có bảng thống kê thời gian sử dụng đèn của chị Nga
từ lúc sạc đầy pin cho đến khi hết pin theo giá trị đại diện như sau:
Thời gian sử
dụng (giờ)
8
10
12
14
16
Số lần
2
5
7
6
3
Cỡ mẫu
2 5 7 6 3 23n
.
Thời gian sử dụng trung bình từ lúc chị Nga sạc đầy pin đèn cho tới khi hết pin là:
2.8 5.10 7.12 6.14 3.16
12,26
23
x
(giờ).
b) Gọi
1 2 23
; ;...;x x x
là mẫu số liệu được xếp theo thứ tự không giảm. Ta có tứ phân vị
thứ nhất của dãy số liệu trên là
6
9;11x
.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
24
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
1
1.23
2
4
9 . 11 9 10,5
5
Q
.
Do
1
Q
gần với 10 nên nhận định của chị Nga là hợp lí.