BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG – MÔN: TOÁN
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – THỜI GIAN: 90 PHÚT
A. Trắc nghiệm (7 điểm):
Câu 1: Góc có số đo rad đổi sang độ là 5 A. 32 . B. 36 . C. 40 . D. 42 .
Câu 2: Công thức số đo tổng quát của góc lượng giác OM ,ON trong hình bên là y M 75° 25° x O A N
A. 100 k360 , k . B. 260 k360 , k . C. 100 k360 , k .
D. 50 k360 , k .
Câu 3: Hải lí là một đơn vị hàng hải, được tính bằng độ dài một cung chắn một góc 1
của đường kinh tuyến (hình vẽ dưới đây). Biết bán kính trung bình Trái 60
Đất là 6371 km. Độ dài 1 hải lí là (làm tròn đến hàng phần trăm) 1
Cực Bắc hải lí α
O Đường xích đạo Cực Nam A. 1,86 km. B. 1,58 km. C. 1,85 km. D. 2,05 km. 5 Câu 4: Cho sin với
. Giá trị của cos là 13 2 12 12 8 8 A. . B. . C. . D. . 13 13 13 13
Câu 5: Đẳng thức nào sau đây là đúng? 2 tan 2 tan A. tan 2 . B. tan 2 . 2 1 tan 2 1 tan 4 tan 2 tan C. tan 2 tan 2 2 1 . D. tan 2 tan . 1
Câu 6: Rút gọn biểu thức 2 cos sin sin 2 , ta được: A. 2sin.cos . B. 2 cos . C. 2 2 cos sin . D. 1.
Câu 7: Giá trị của cos.cos bằng giá trị của biểu thức nào sau đây với mọi , ? 1 1 A.
cos cos .
B. cos cos . 2 2 1 1 C.
sin sin . D.
cos sin . 2 2
Câu 8: Tập giá trị của hàm y cos x là A. . B. 1 ; 1 . C. \ 0 . D. \ 1 ; 1 . 2
x
Câu 9: Hàm số y 5cos có chu kì là 2 3 A. 4 . B. . C. . D. 2 . 2 cos 2x
Câu 10: Tập xác định của hàm số y là sin x 1 A.
\ k2 ,k . B. . 2 C. \ 0 . D.
\ k ,k . 2
Câu 11: Giá trị nhỏ nhất của hàm số y 3 sin x là 3 A. 3 . B. 1 . C. 1. D. 3 .
Câu 12: Phương trình 3 sin x 0 có tập nghiệm là 2 4 A. S
k2;k . B. S
k2;k . 3 3 4 4 C. S k2;
k2;k . D. S k2;
k2;k . 3 3 3 3
Câu 13: Điều kiện của tham số m để phương trình sin 2x m có nghiệm là 4 A. 1 m 1. B. m 1. C. m 1 . D. m 1 .
Câu 14: Nghiệm của phương trình tan x 3 0 được biểu diễn trên đường tròn
lượng giác ở hình dưới đây là những điểm nào? 3
y D C E B O x A F K G I H
A. Điểm C và điểm F .
B. Điểm G và điểm A .
C. Điểm I và điểm D .
D. Điểm B và điểm F .
Câu 15: Tổng các nghiệm của phương trình sin 2x cos x trong khoảng 3 0;6 là 17 25 35 A. . B. 3 . C. . D. . 6 18 18
Câu 16: Dãy số nào dưới đây là dãy tăng? 1
A. u với u .
B. u với u 3 n 5 . n n n n 1 n 2
C. u với u .
D. u với u 2n 3. n n n 2 n n
Câu 17: Cách liệt kê nào là đúng với dãy số sau: Dãy số gồm tất cả các số nguyên tố
lẻ nhỏ hơn 20 theo thứ tự tăng dần.
A. 2; 3; 5; 7; 9; 11; 13; 15; 17; 19.
B. 3; 5; 7; 9; 11; 13; 15; 17; 19.
C. 3; 5; 7; 11; 13; 17; 19.
D. 2; 3; 5; 7; 11; 13; 17; 19. n
Câu 18: Cho dãy số u với u n n
3n . Ba số hạng đầu tiên của dãy số đó lần lượt 1
là những số nào dưới đây? 4
Đề thi giữa kì 1 Toán 11 Kết nối tri thức (đề 6)
500
250 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ 10 đề giữa kì 1 gồm đầy đủ ma trận và lời giải chi tiết môn Toán 11 bộ Kết nối tri thức mới nhất năm 2023 - 2024 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 11.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(500 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 45 đề thi cuối kì 1 Toán 11 Kết nối tri thức Cấu trúc mới180.000 ₫ 6.8 K 3.4 K lượt tải
-
Bộ 27 đề thi cuối kì 1 Toán 11 Chân trời sáng tạo Cấu trúc mới180.000 ₫ 2.6 K 1.3 K lượt tải
-
Bộ 39 đề thi cuối kì 1 Toán 11 Cánh diều Cấu trúc mới180.000 ₫ 3 K 1.5 K lượt tải
-
Bộ 35 đề thi giữa kì 1 Toán 11 Kết nối tri thức Cấu trúc mới150.000 ₫ 18.3 K 9.1 K lượt tải
-
Bài tập Toán 11 Kết nối tri thức (Dạy thêm - có lời giải)300.000 ₫ 2.9 K 1.4 K lượt tải
-
Giáo án Toán 11 Cánh diều | Giáo án Toán 11 mới, chuẩn nhất300.000 ₫ 3.1 K 1.6 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Toán 11 Chân trời sáng tạo Cấu trúc mới150.000 ₫ 5.4 K 2.7 K lượt tải
-
Giáo án điện tử Toán 11 (sách mới) | Bài giảng Powerpoint (PPT) Toán 11300.000 ₫ 309 155 lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 11
Xem thêm-
Bộ 4 đề thi giữa kì 1 Tin học 11 Kết nối tri thức có đáp án80.000 ₫ 20.4 K 10.2 K lượt tải
-
Bài giảng Powerpoint Địa lí 11 Chân trời sáng tạo200.000 ₫ 5.4 K 2.7 K lượt tải
-
Bộ 4 đề thi giữa kì 1 Tin học 11 Cánh diều có đáp án80.000 ₫ 6.4 K 3.2 K lượt tải
-
Trắc nghiệm Lịch sử 11 Đúng-Sai (form 2025200.000 ₫ 7.9 K 3.9 K lượt tải
-
Chuyên đề dạy thêm Vật lí 11 (sách mới) năm 2024 có đáp án200.000 ₫ 8.8 K 4.4 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Lịch sử 11 Kết nối tri thức có đáp án70.000 ₫ 9.9 K 4.9 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Lịch sử 11 Cánh diều có đáp án70.000 ₫ 7.4 K 3.7 K lượt tải
-
Chuyên đề dạy thêm Hóa 11 (cấu trúc mới)200.000 ₫ 6.2 K 3.1 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
1
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG – MÔN: TOÁN
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – THỜI GIAN: 90 PHÚT
A. Trắc nghiệm (7 điểm):
Câu 1: Góc có số đo
5
rad đổi sang độ là
A.
32
. B.
36
. C.
40
. D.
42
.
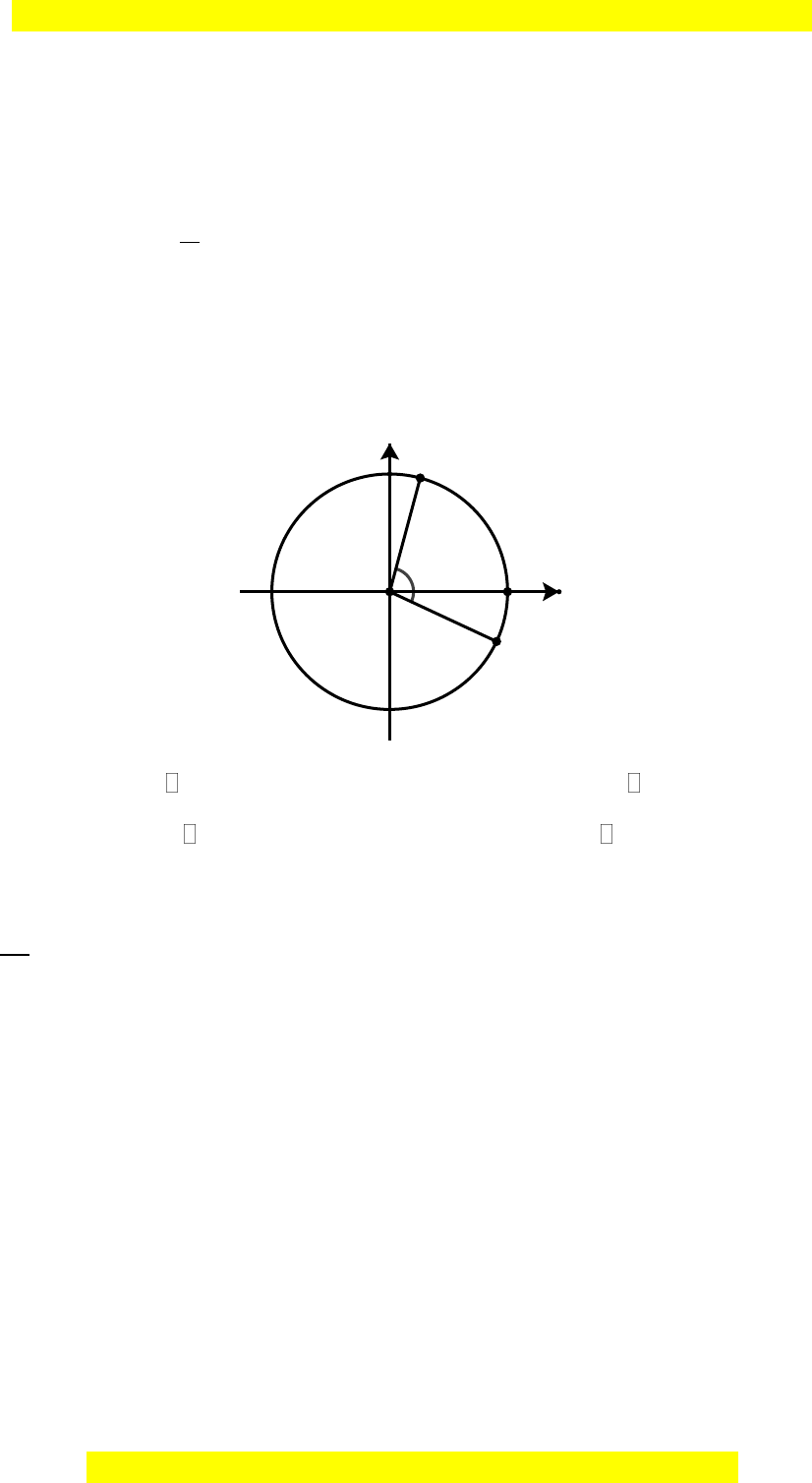
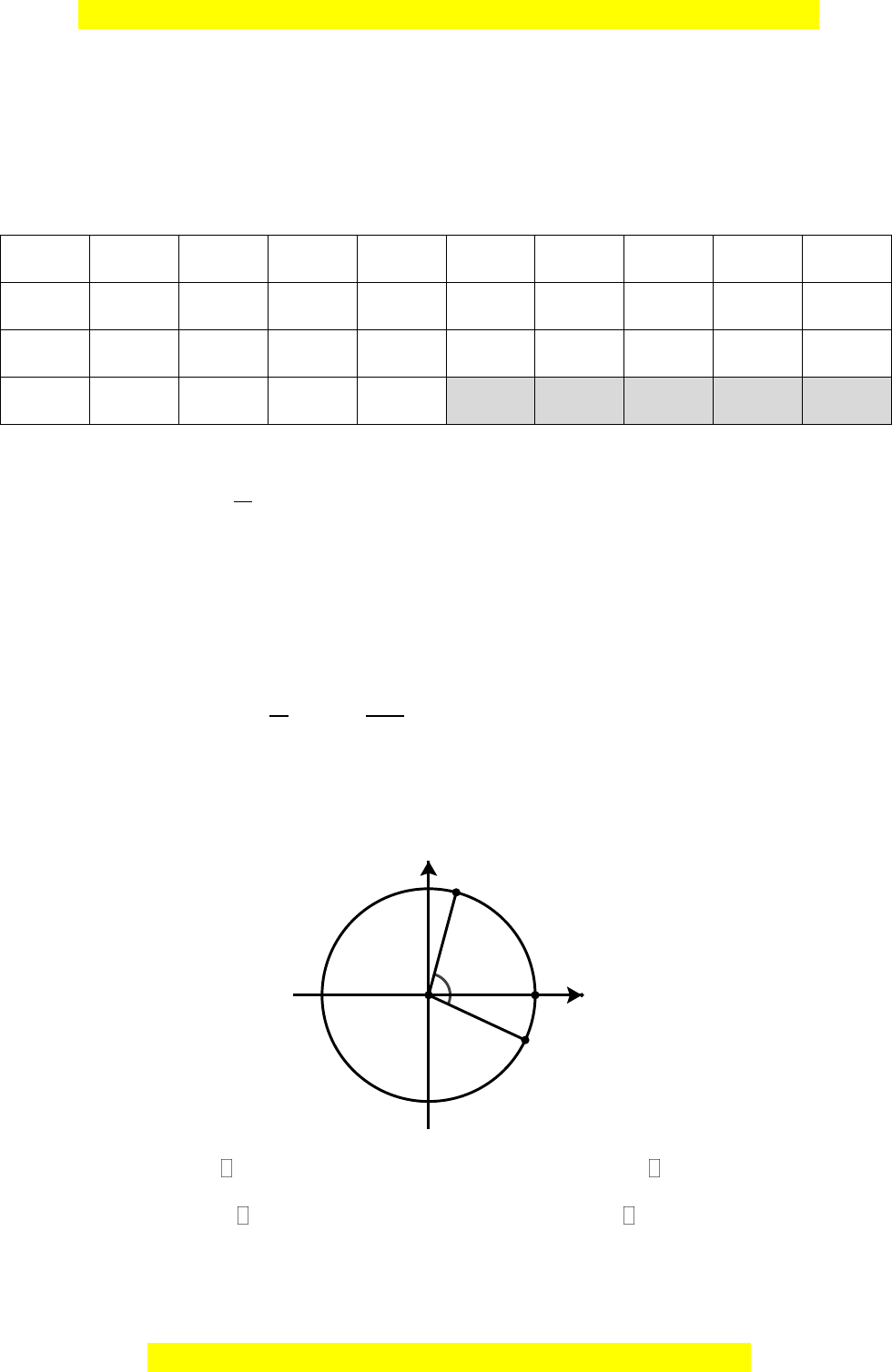
Câu 2: Công thức số đo tổng quát của góc lượng giác
,OM ON
trong hình bên là
A.
100 360 ,kk
. B.
260 360 ,kk
.
C.
100 360 ,kk
. D.
50 360 ,kk
.
Câu 3: Hải lí là một đơn vị hàng hải, được tính bằng độ dài một cung chắn một góc
1
60
của đường kinh tuyến (hình vẽ dưới đây). Biết bán kính trung bình Trái
Đất là 6371 km. Độ dài 1 hải lí là (làm tròn đến hàng phần trăm)
25
°
75
°
y
x
N
M
O
A
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
2
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. 1,86 km. B. 1,58 km. C. 1,85 km. D. 2,05 km.
Câu 4: Cho
5
sin
13
với
2
. Giá trị của
cos
là
A.
12
13
. B.
12
13
. C.
8
13
. D.
8
13
.
Câu 5: Đẳng thức nào sau đây là đúng?
A.
2
2tan
tan 2
1 tan
. B.
2
2tan
tan 2
1 tan
.
C.
2
4tan
tan 2
1 tan
. D.
2
2tan
tan 2
tan 1
.
Câu 6: Rút gọn biểu thức
2
cos sin sin2
, ta được:
A.
2sin .cos
. B.
2
cos
.
C.
22
cos sin
. D. 1.
Câu 7: Giá trị của
cos .cos
bằng giá trị của biểu thức nào sau đây với mọi
,
?
A.
1
cos cos
2
. B.
1
cos cos
2
.
C.
1
sin sin
2
. D.
1
cos sin
2
.
Câu 8: Tập giá trị của hàm
cosyx
là
A. . B.
1;1
. C.
\0
. D.
\ 1;1
.
α
hải lí
Cực Bắc
Cực Nam
Đường xích đạo
O
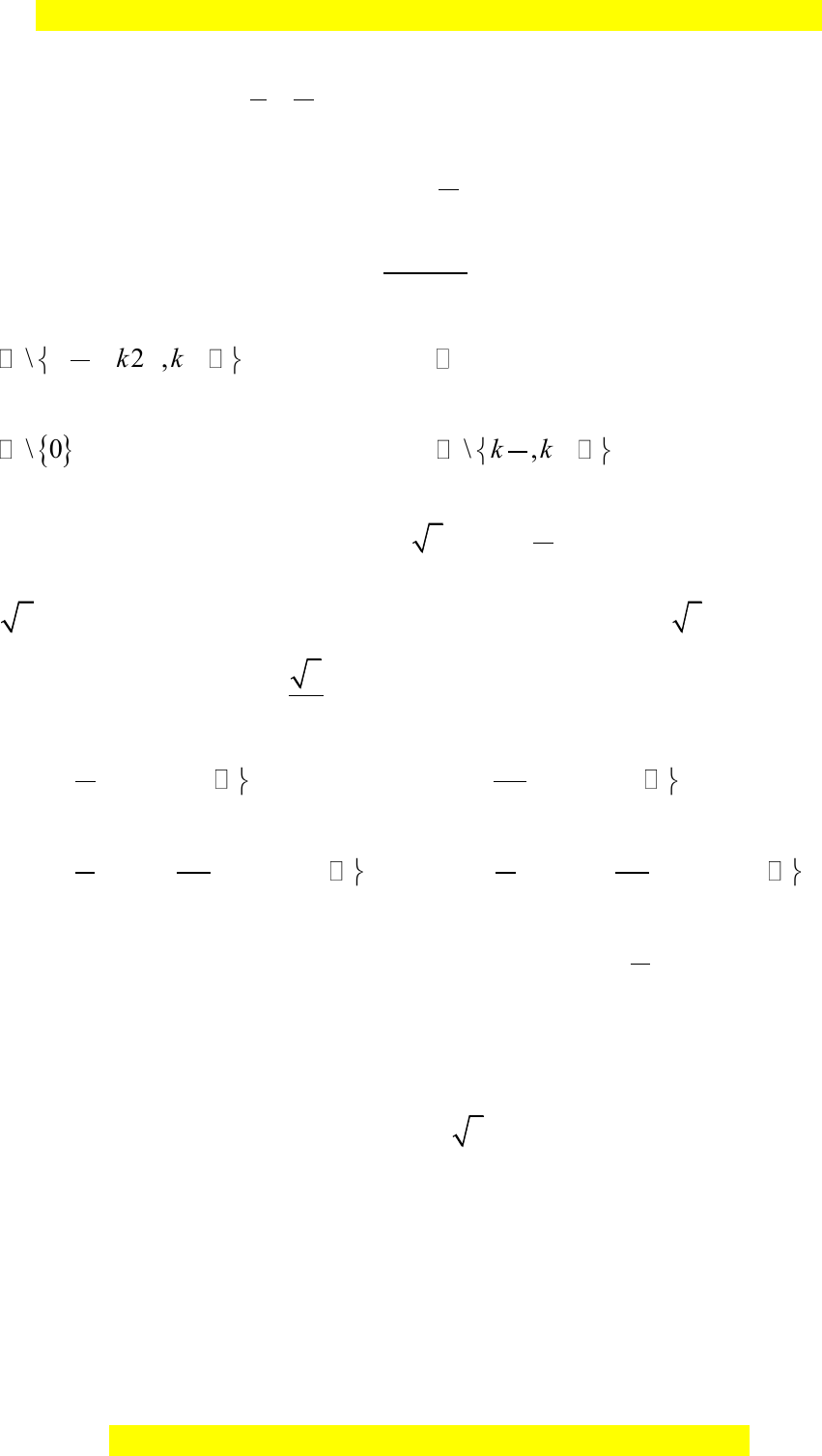
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
3
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 9: Hàm số
5cos
23
x
y
có chu kì là
A.
4
. B.
. C.
2
. D.
2
.
Câu 10: Tập xác định của hàm số
cos2
sin 1
x
y
x
là
A.
\ 2 ,
2
kk
. B. .
C.
\0
. D.
\,
2
kk
.
Câu 11: Giá trị nhỏ nhất của hàm số
3sin
3
yx
là
A.
3
. B.
1
. C.
1
. D.
3
.
Câu 12: Phương trình
3
sin 0
2
x
có tập nghiệm là
A.
2;
3
S k k
. B.
4
2;
3
S k k
.
C.
4
2 ; 2 ;
33
S k k k
. D.
4
2 ; 2 ;
33
S k k k
.
Câu 13: Điều kiện của tham số
m
để phương trình
sin 2
4
xm
có nghiệm là
A.
11m
. B.
1m
.
C.
1m
. D.
1m
.
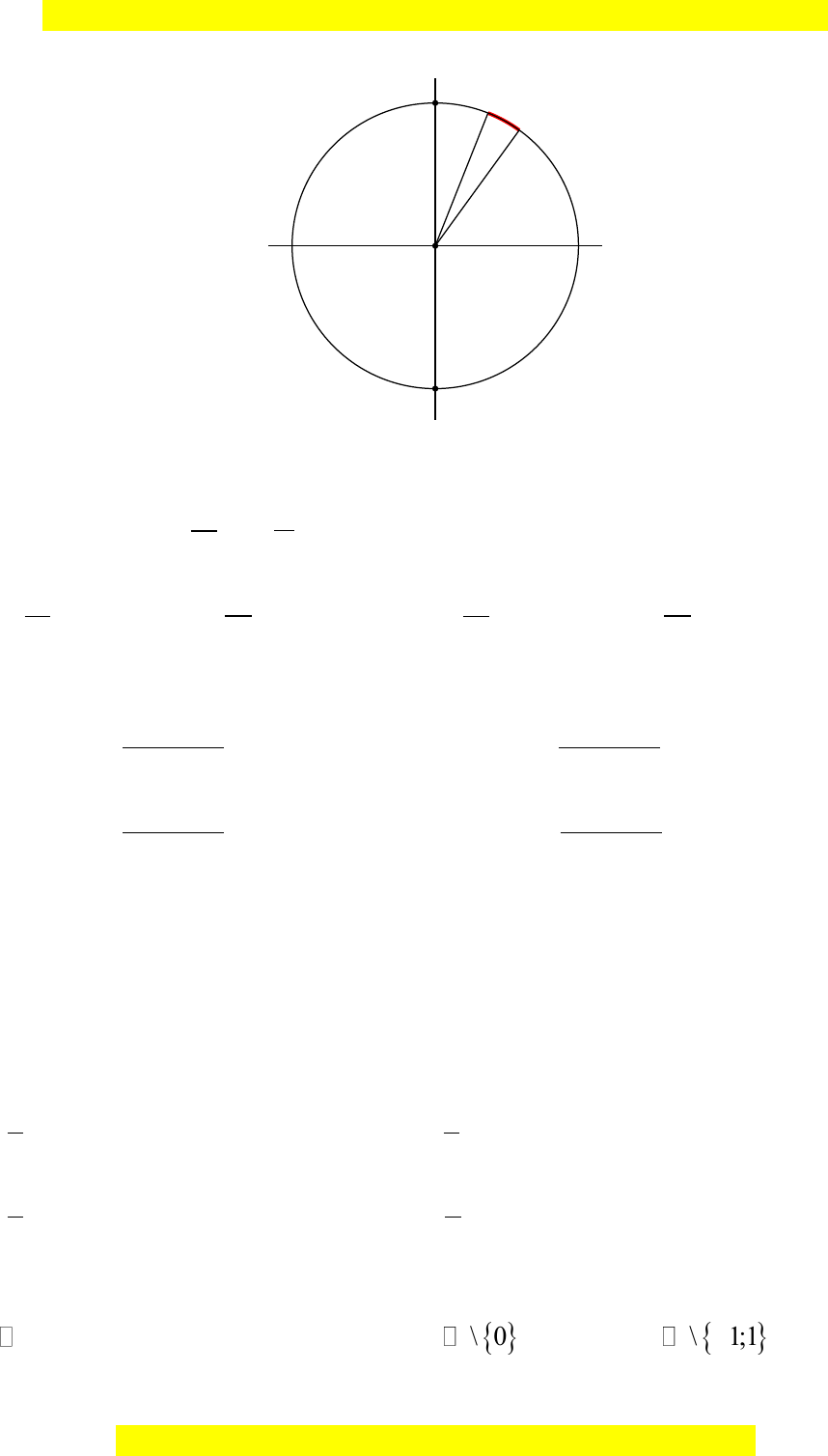
Câu 14: Nghiệm của phương trình
tan 3 0x
được biểu diễn trên đường tròn
lượng giác ở hình dưới đây là những điểm nào?
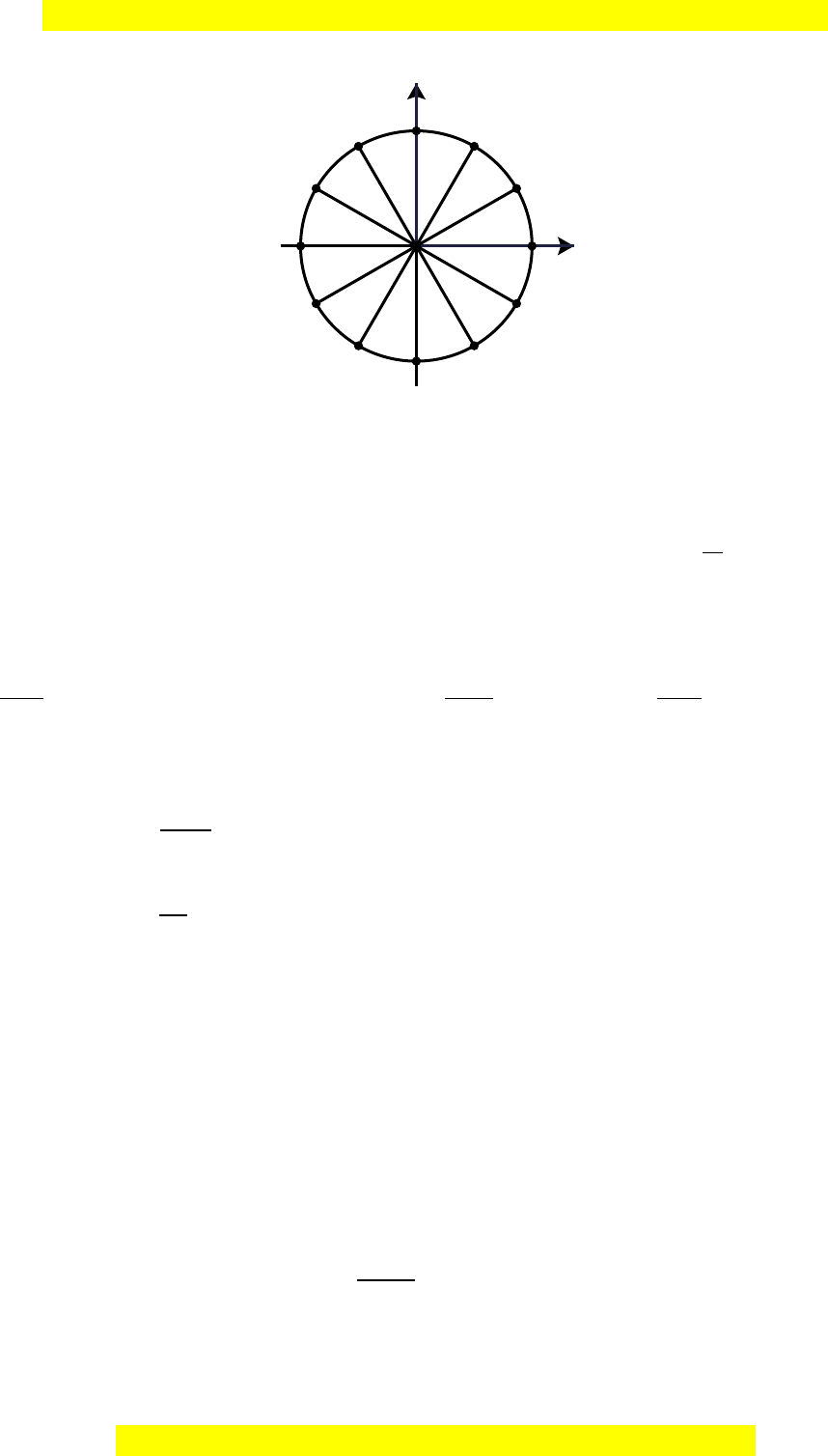
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
4
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. Điểm
C
và điểm
F
. B. Điểm
G
và điểm
A
.
C. Điểm
I
và điểm
D
. D. Điểm
B
và điểm
F
.
Câu 15: Tổng các nghiệm của phương trình
sin 2 cos
3
xx
trong khoảng
0;6
là
A.
17
6
. B.
3
. C.
25
18
. D.
35
18
.
Câu 16: Dãy số nào dưới đây là dãy tăng?
A.
n
u
với
1
1
n
u
n
. B.
n
u
với
35
n
un
.
C.
n
u
với
2
2
n
u
n
. D.
n
u
với
23
n
un
.
Câu 17: Cách liệt kê nào là đúng với dãy số sau: Dãy số gồm tất cả các số nguyên tố
lẻ nhỏ hơn 20 theo thứ tự tăng dần.
A. 2; 3; 5; 7; 9; 11; 13; 15; 17; 19.
B. 3; 5; 7; 9; 11; 13; 15; 17; 19.
C. 3; 5; 7; 11; 13; 17; 19.
D. 2; 3; 5; 7; 11; 13; 17; 19.
Câu 18: Cho dãy số
n
u
với
31
n
n
n
u
. Ba số hạng đầu tiên của dãy số đó lần lượt
là những số nào dưới đây?
y
x
G
F
D
I
K
E
C
B
O
A
H
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
5
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
1 1 1
;;
2 4 8
. B.
1 1 3
;;
2 4 26
. C.
1 1 1
;;
2 4 16
. D.
1 2 3
;;
234
.
Câu 19: Cho dãy số
n
u
với
31
31
n
n
u
n
. Dãy số
n
u
bị chặn trên bởi số nào dưới
đây?
A.
1
3
. B. 1. C.
1
2
. D. 0.
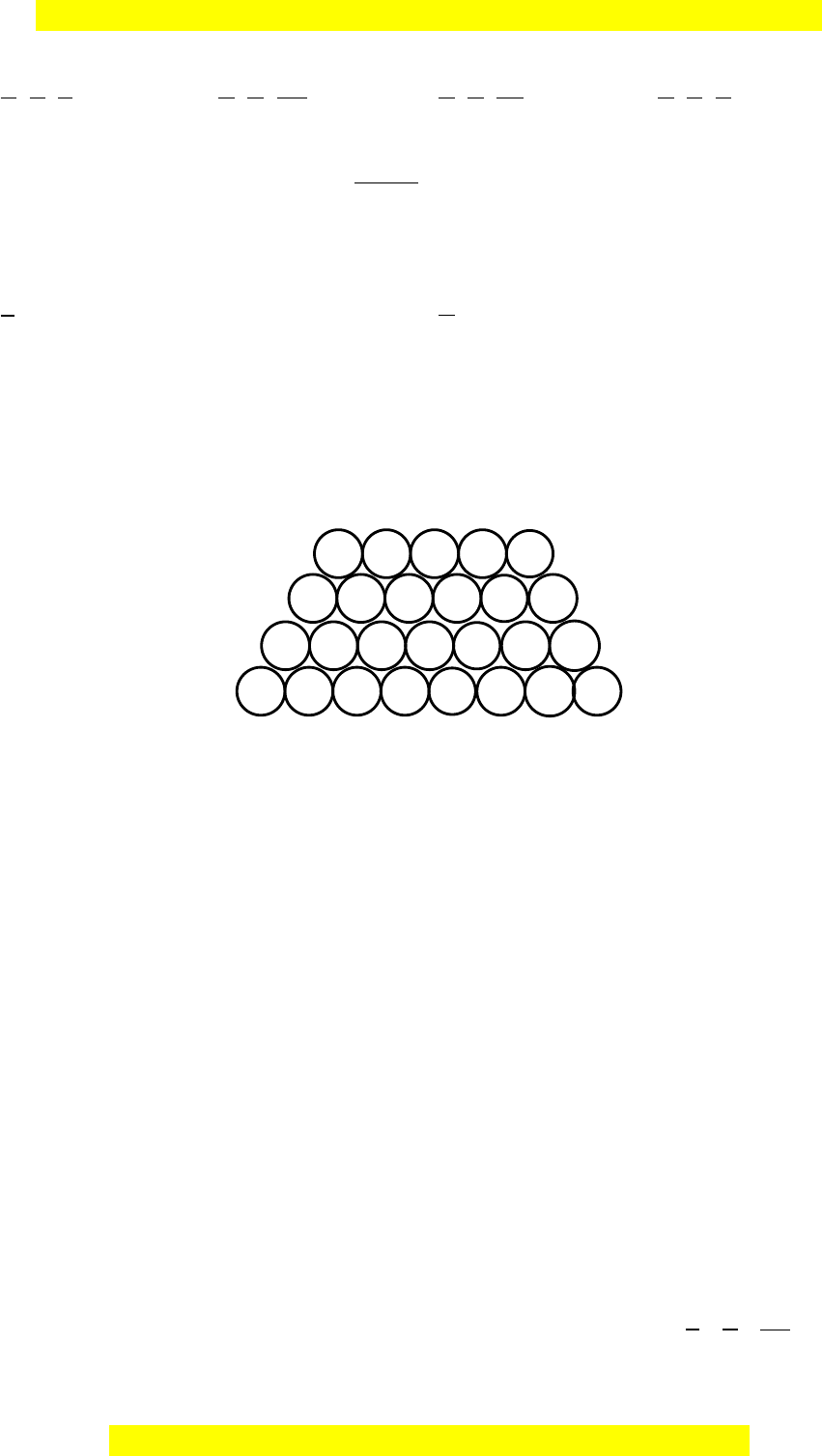
Câu 20: Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1
cột gỗ (Hình vẽ). Gọi
n
u
là số cột gỗ nằm ở lớp thứ
n
tính từ trên xuống và cho biết
lớp trên cùng có 14 cột gỗ. Số hạng tổng quát dãy số
n
u
là
A.
14
n
un
. B.
13
n
un
.
C.
14 2
n
un
. D.
14 2 1
n
un
.
Câu 21: Cho cấp số cộng có số hạng đầu là 5, số hạng thứ 8 là 40. Khi đó công sai
của cấp số cộng đó bằng bao nhiêu?
A. 5. B. 6. C. 7. D. 2.
Câu 22: Cho cấp số cộng
n
u
có
1
4u
và
5d
. Tổng 100 số hạng đầu tiên của
cấp số cộng
n
u
là
A. –24530. B. –24350. C. –23450. D. –32450.
Câu 23: Giá trị của
x
để ba số
6; ;20x
lập thành một cấp số cộng là
A.
12x
. B.
10x
. C.
15x
. D.
13x
.
Câu 24: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. 2; 4; 8; 16;…. B. 1; -1 ;1;-1;… C. 1; 4; 9; 16;…. D. 1;
1
3
;
1
9
;
1
27
;….
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
6
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 25: Cho cấp số nhân
n
u
với
3
45u
,
5
80u
. Giá trị của
4
u
là
A.
4
60u
. B.
4
50u
. C.
4
40u
. D.
4
55u
.
Câu 26: Cho cấp số nhân
n
u
với
1
3u
và
2q
. Số 192 là số hạng thứ mấy của
cấp số nhân đã cho?
A. Số hạng thứ 5. B. Số hạng thứ 6.
C. Số hạng thứ 7. D. Số hạng thứ 9.
Câu 27: Cho cấp số nhân
n
u
có
1
0u
và
0q
. Với
1 km
, đẳng thức nào sau
đây là đúng?
A.
.
k
mk
u u q
. B.
.
m
mk
u u q
.
C.
.
mk
mk
u u q
. D.
.
mk
mk
u u q
.
Câu 28: Cho tam giác
ABC
và một điểm
O
không thuộc mặt phẳng
ABC
. Giao
tuyến của hai mặt phẳng
OAB
và
ABC
là
A.
OA
. B.
AB
.
C.
BC
. D.
AC
.
Câu 29: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt. B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau. D. Bốn điểm phân biệt.
Câu 30: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.
B. Hai đường thẳng song song khi và chỉ khi chúng không có điểm chung.
C. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
D. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
Câu 31: Cho điểm
A
không nằm trên mặt phẳng
chứa tam giác
BCD
. Lấy
,EF
là các điểm lần lượt nằm trên các cạnh
,AB AC
. Khi
EF
và
BC
cắt nhau tại
I
, thì
I
không phải là điểm chung của hai mặt phẳng nào sau đây?
A.
BCD
và
DEF
. B.
BCD
và
ABC
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
7
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C.
BCD
và
AEF
. D.
BCD
và
ABD
.
Câu 32: Cho hai đường thẳng chéo nhau
a
và
b
. Lấy
A
,
B
thuộc
a
và
C
,
D
thuộc
b
. Khẳng định nào sau đây là đúng khi nói về hai đường thẳng
AD
và
BC
?
A. Có thể song song hoặc cắt nhau. B. Cắt nhau.
C. Song song với nhau. D. Chéo nhau.
Câu 33: Trong không gian, cho 3 đường thẳng
,,abc
. Biết
//ab
,
a
và
c
chéo nhau.
Khi đó hai đường thẳng
b
và
c
:
A. Trùng nhau hoặc chéo nhau. B. Cắt nhau hoặc chéo nhau.
C. Chéo nhau hoặc song song. D. Song song hoặc trùng nhau.
Câu 34: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
d
là giao
tuyến của hai mặt phẳng
SAD
và
SBC
. Khẳng định nào sau đây là đúng?
A.
d
qua
S
và song song với
BC
. B.
d
qua
S
và song song với
DC
.
C.
d
qua
S
và song song với
AB
. D.
d
qua
S
và song song với
BD
.
Câu 35: Cho tứ diện
ABCD
. Gọi
I
,
J
lần lượt là trọng tâm các tam giác
ABC
và
ABD
. Chọn khẳng định đúng trong các khẳng định sau:
A.
IJ
song song với
CD
. B.
IJ
song song với
AB
.
C.
IJ
song song với
BC
. D.
IJ
song song với
BD
.
B. Tự luận (3 điểm):
Câu 1: Giải các phương trình sau:
a)
sin cos 2
46
xx
;
b)
2
2cos 5sin 4 0xx
.
c)
3 sin cos 2sin2 3 0x x x
.
Câu 2: Cho hình chóp
.S ABCD
có đáy là hình thang đáy lớn là
AB
. Gọi
M
,
N
lần
lượt là trung điểm của
SA
và
SB
.
a) Chứng minh rằng:
//MN CD
.
b) Xác định giao tuyến của mặt phẳng
AND
với mặt phẳng
SAC
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
8
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
c) Gọi
P
là giao điểm giữa
SC
và mặt phẳng
AND
. Kéo dài
AN
và
DP
cắt nhau
tại
I
. Chứng minh rằng
// //SI AB CD
. Tứ giác
SIBA
là hình gì?
Câu 3: Cho dãy số
n
u
với
n
an b
u
cn d
với
, , ,a b c d
là các số thực và
0cn d
với mọi
*
n
.
a) Chứng minh rằng: Nếu
0ad bc
thì
n
u
là một dãy tăng, còn
0ad bc
thì
n
u
là một dãy giảm và khi
0ad bc
thì
n
u
là một dãy không thay đổi, tức là
12
...
n
u u u
.
b) Tính giá trị của các số hạng trong dãy khi dãy
n
u
là dãy không thay đổi.
----- HẾT-----
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
9
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
BỘ SÁCH: KẾT NỐI TRI THỨC VỚI CUỘC SỐNG – MÔN: TOÁN
ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI
ĐỀ KIỂM TRA GIỮA HỌC KÌ 1 – THỜI GIAN: 90 PHÚT
I. Bảng đáp án trắc nghiệm
1. B
2. C
3. C
4. A
5. A
6. D
7. A
8. B
9. A
10. A
11. A
12. C
13. A
14. C
15. B
16. D
17. C
18. B
19. B
20. B
21. A
22. B
23. D
24. C
25. A
26. C
27. C
28. B
29. C
30. D
31. D
32. D
33. B
34. A
35. A
II. Hướng dẫn giải trắc nghiệm
Câu 1: Góc có số đo
5
rad đổi sang độ là
A.
32
. B.
36
. C.
40
. D.
42
.
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
180
(rad)
180
rad 36
55
.
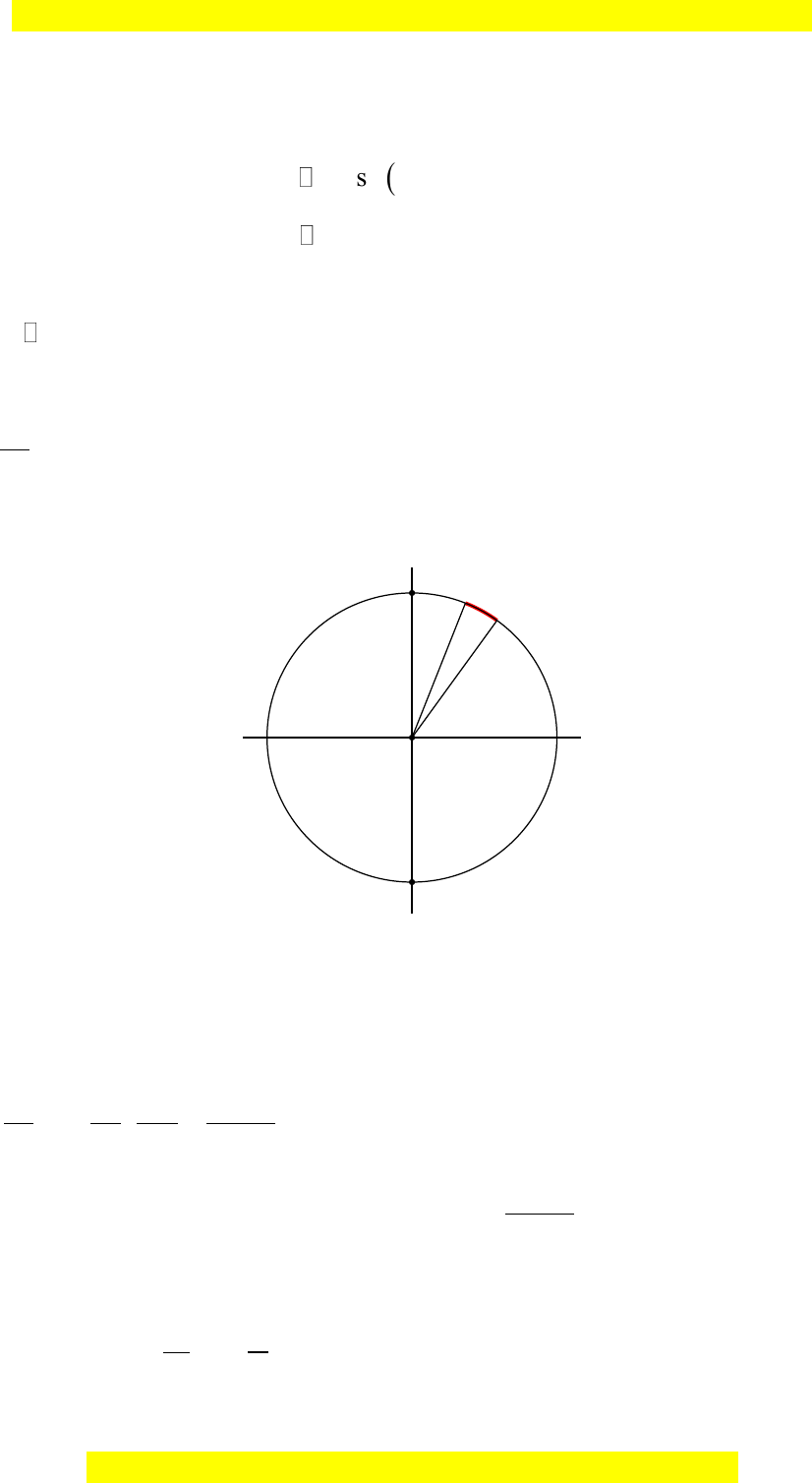
Câu 2: Công thức số đo tổng quát của góc lượng giác
,OM ON
trong hình bên là
A.
100 360 ,kk
. B.
260 360 ,kk
.
C.
100 360 ,kk
. D.
50 360 ,kk
.
Hướng dẫn giải:
25
°
75
°
y
x
N
M
O
A
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
10
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đáp án đúng là: C.
Từ hình vẽ, ta có:
s s , 75, 3, 75 360 60kOA OM m mđ đ OM OA
.
, 25 360 ,s OA ON n nđ
.
, , , 75 25 360 100 360sđ OM ON sđ OM OA sđ OA ON k k
với
k
.
Câu 3: Hải lí là một đơn vị hàng hải, được tính bằng độ dài một cung chắn một góc
1
60
của đường kinh tuyến (hình vẽ dưới đây). Biết bán kính trung bình Trái
Đất là 6 371 km. Độ dài 1 hải lí là (làm tròn đến hàng phần trăm)
A. 1,86 km. B. 1,58 km. C. 1,85 km. D. 2,05 km.
Hướng dẫn giải:
Đáp án đúng là: C.
Đổi
11
60 60 180 10800
rad.
Khi đó, độ dài cung chắn góc
là:
6371 1,85
10800
lR
(km).
Vậy 1 hải lí
1,85
km.
Câu 4: Cho
5
sin
13
với
2
. Giá trị của
cos
là
α
hải lí
Cực Bắc
Cực Nam
Đường xích đạo
O
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
11
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
12
13
. B.
12
13
. C.
8
13
. D.
8
13
.
Hướng dẫn giải:
Đáp án đúng là: A.
Vì
2
nên
0 sin 1
1 cos 0
.
Ta có:
2
2 2 2
5
sin cos 1 cos 1
13
2
144 12
cos cos
169 13
(vì
1 cos 0
).
Vậy
12
cos
13
.
Câu 5: Đẳng thức nào sau đây là đúng?
A.
2
2tan
tan 2
1 tan
. B.
2
2tan
tan 2
1 tan
.
C.
2
4tan
tan 2
1 tan
. D.
2
2tan
tan 2
tan 1
.
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
2
2tan
tan 2
1 tan
.
Câu 6: Rút gọn biểu thức
2
cos sin sin2
, ta được:
A.
2sin .cos
. B.
2
cos
.
C.
22
cos sin
. D. 1.
Hướng dẫn giải:
Đáp án đúng là: D.
2
22
cos sin sin2 sin cos 2sin .cos 2sin .cos
22
sin cos 1
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
12
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy
2
cos sin sin2 1
.
Câu 7: Giá trị của
cos .cos
bằng giá trị của biểu thức nào sau đây với mọi
,
?
A.
1
cos cos
2
. B.
1
cos cos
2
.
C.
1
sin sin
2
. D.
1
cos sin
2
.
Hướng dẫn giải:
Đáp án đúng là: A.
1
cos .cos cos cos
2
.
Câu 8: Tập giá trị của hàm
cosyx
là
A. . B.
1;1
. C.
\0
. D.
\ 1;1
.
Hướng dẫn giải:
Đáp án đúng là: B.
Hàm số
cosyx
có tập giá trị là
1;1
.
Câu 9: Hàm số
5cos
23
x
y
có chu kì là
A.
4
. B.
. C.
2
. D.
2
.
Hướng dẫn giải:
Đáp án đúng là: A.
Chu kì của hàm số
5tan
23
x
y
là:
2
4
1
2
.
Câu 10: Tập xác định của hàm số
cos2
sin 1
x
y
x
là
A.
\ 2 ,
2
kk
. B. .
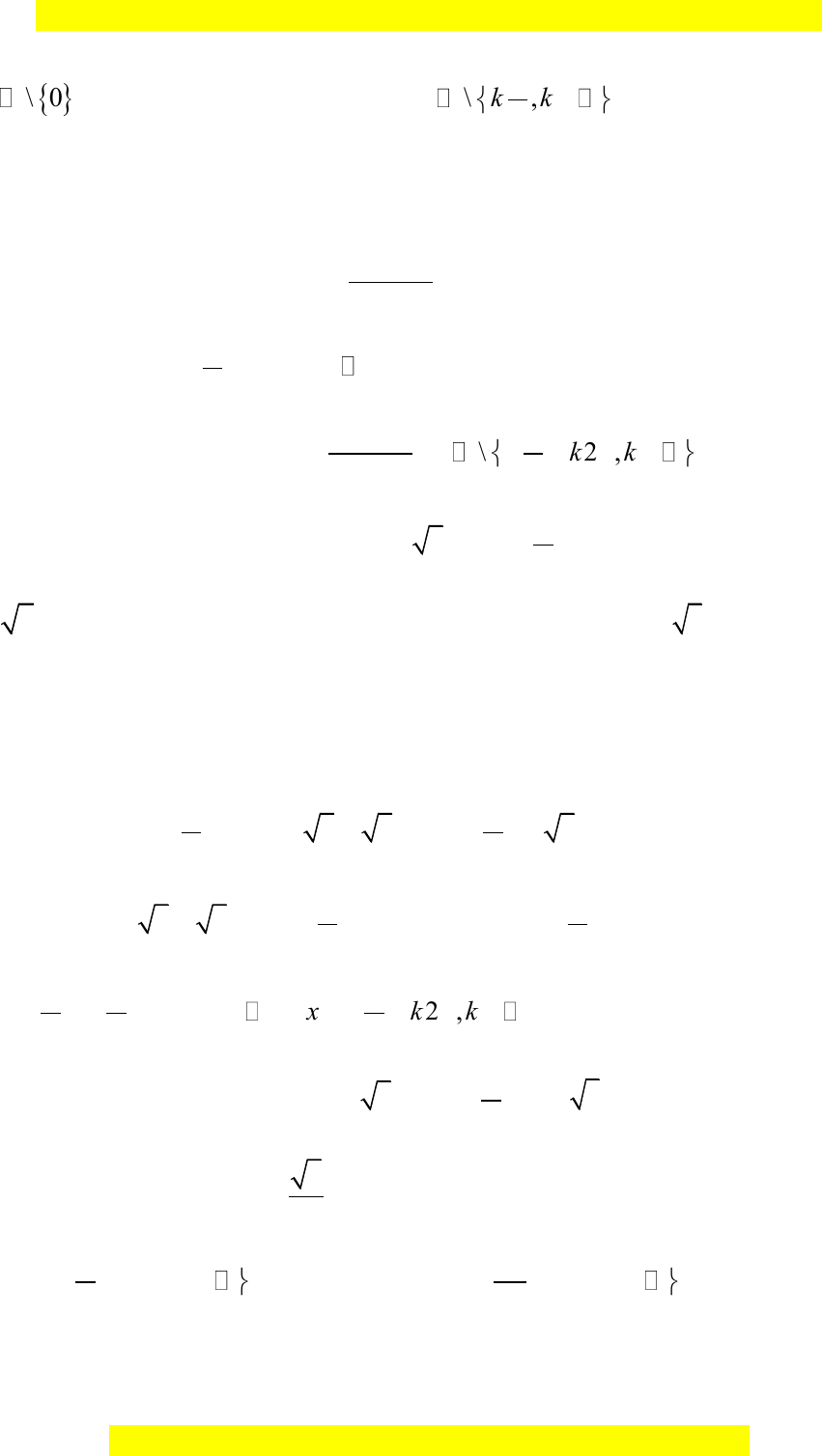
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
13
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C.
\0
. D.
\,
2
kk
.
Hướng dẫn giải:
Đáp án đúng là: A.
Điều kiện xác định của hàm số
cos2
sin 1
x
y
x
là
sin 1 0x
sin 1 2 ,
2
x x k k
.
Vậy tập xác định của hàm số
cos2
sin 1
x
y
x
là
\ 2 ,
2
kk
.
Câu 11: Giá trị nhỏ nhất của hàm số
3sin
3
yx
là
A.
3
. B.
1
. C.
1
. D.
3
.
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
1 sin 1 3 3sin 3
33
xx
.
Dấu
""
của
3 3sin
3
x
xảy ra khi
sin 1
3
x
2 , 2 ,
3 2 6
x k k x k k
.
Vậy giá trị nhỏ nhất của hàm số
3sin
3
yx
là
3
.
Câu 12: Phương trình
3
sin 0
2
x
có tập nghiệm là
A.
2;
3
S k k
. B.
4
2;
3
S k k
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
14
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C.
4
2 ; 2 ;
33
S k k k
. D.
4
2 ; 2 ;
33
S k k k
.
Hướng dẫn giải:
Đáp án đúng là: C.
33
sin 0 sin
22
xx
2
2
3
3
,,
4
2
2
3
3
xk
xk
kk
xk
xk
Vậy tập nghiệm của phương trình là:
4
2 ; 2 ;
33
S k k k
.
Câu 13: Điều kiện của tham số
m
để phương trình
sin 2
4
xm
có nghiệm là
A.
11m
. B.
1m
.
C.
1m
. D.
1m
.
Hướng dẫn giải:
Đáp án đúng là: A.
Vì
1 sin 2 1
4
x
nên phương trình
sin 2
4
xm
có nghiệm khi và chỉ khi
11m
.
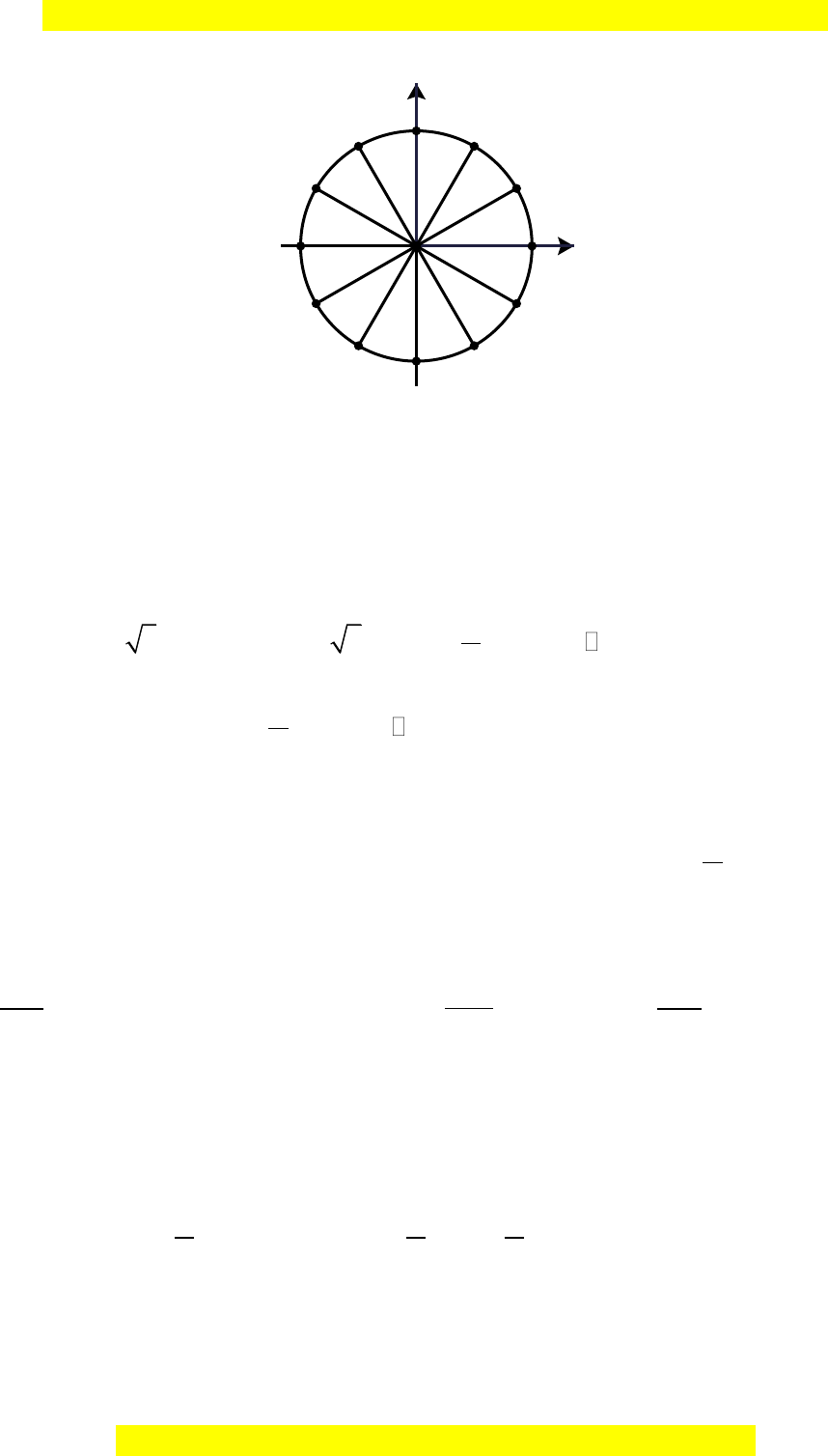
Câu 14: Nghiệm của phương trình
tan 3 0x
được biểu diễn trên đường tròn
lượng giác ở hình dưới đây bởi những điểm nào?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
15
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. Điểm
C
và điểm
F
. B. Điểm
G
và điểm
A
.
C. Điểm
I
và điểm
D
. D. Điểm
B
và điểm
F
.
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
tan 3 0 tan 3 ,
3
x x x k k
.
Điểm biểu diễn của
,
3
x k k
trên đường tròn lượng giác là điểm
I
và
điểm
D
.
Câu 15: Tổng các nghiệm của phương trình
sin 2 cos
3
xx
trong khoảng
0;6
là
A.
17
6
. B.
3
. C.
25
18
. D.
35
18
.
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
sin 2 cos sin 2 sin
3 2 3
x x x x
y
x
G
F
D
I
K
E
C
B
O
A
H
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
16
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
5
22
6
5
sin 2 sin ,
5
6
22
6
x x k
x x k
x x k
5 5 2
32
6 18 3
,,
22
66
x k x k
kk
x k x k
Vì
0;6x
nên ta có:
+)
5 2 5 2 5 5 9 5
0 6 6
18 3 18 3 18 12 12
k k k
0;1;2k
(vì
k
)
5 17 29
;;
18 18 18
x
.
+)
1 3 1
0 2 6 2 6
6 6 6 12 12
k k k
0k
(vì
k
)
6
x
.
Vậy tổng các nghiệm thoả mãn yêu cầu đề bài là:
5 17 29
3
18 18 18 6
S
.
Câu 16: Dãy số nào dưới đây là dãy tăng?
A.
n
u
với
1
1
n
u
n
. B.
n
u
với
35
n
un
.
C.
n
u
với
2
2
n
u
n
. D.
n
u
với
23
n
un
.
Hướng dẫn giải:
Đáp án đúng là: D.
Xét dãy số
n
u
với
23
n
un
:
11
2 1 3 2 3 2 0
n n n n
u u n n u u
.
Do đó dãy số
n
u
là một dãy tăng.
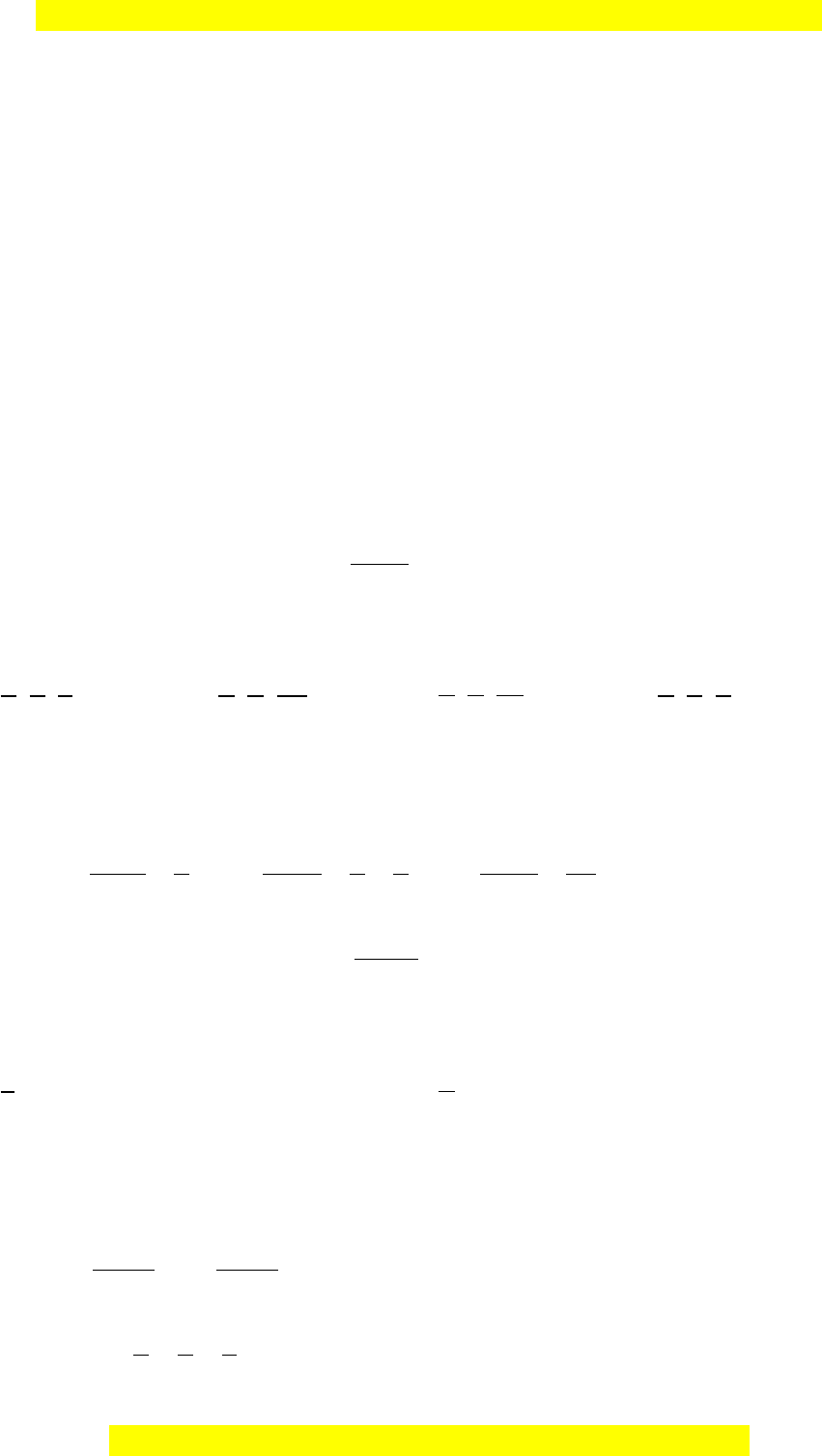
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
17
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 17: Cách liệt kê nào là đúng với dãy số sau: Dãy số gồm tất cả các số nguyên tố
lẻ nhỏ hơn 20 theo thứ tự tăng dần.
A. 2; 3; 5; 7; 9; 11; 13; 15; 17; 19.
B. 3; 5; 7; 9; 11; 13; 15; 17; 19.
C. 3; 5; 7; 11; 13; 17; 19.
D. 2; 3; 5; 7; 11; 13; 17; 19.
Hướng dẫn giải:
Đáp án đúng là: C.
Dãy số gồm tất cả các số nguyên tố lẻ nhỏ hơn 20 theo thứ tự tăng dần là:
3; 5; 7; 11; 13; 17; 19
Câu 18: Cho dãy số
n
u
với
31
n
n
n
u
. Ba số hạng đầu tiên của dãy số đó lần lượt
là những số nào dưới đây?
A.
1 1 1
;;
2 4 8
. B.
1 1 3
;;
2 4 26
. C.
1 1 1
;;
2 4 16
. D.
1 2 3
;;
234
.
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
1
1
11
3 1 2
u
;
2
2
2 2 1
3 1 8 4
u
;
3
3
33
3 1 26
u
.
Câu 19: Cho dãy số
n
u
với
31
31
n
n
u
n
. Dãy số
n
u
bị chặn trên bởi số nào dưới
đây?
A.
1
3
. B. 1. C.
1
2
. D. 0.
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có:
3 1 2
11
3 1 3 1
n
n
u
nn
.
Mặt khác,
2
5 1 1
0
7 2 3
u
nên dãy số
n
u
bị chặn trên bởi số 1.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
18
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
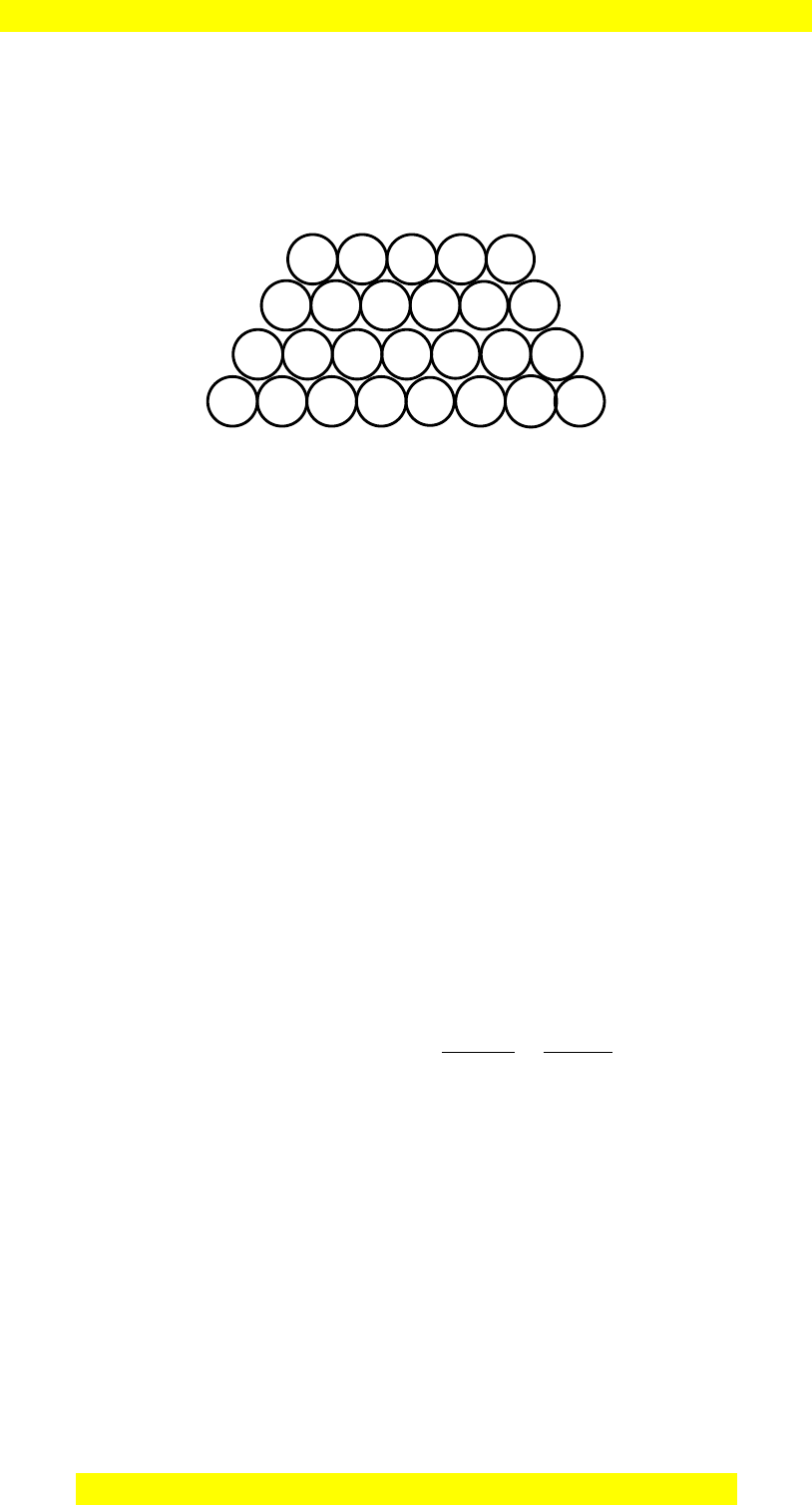
Câu 20: Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1
cột gỗ (Hình vẽ). Gọi
n
u
là số cột gỗ nằm ở lớp thứ
n
tính từ trên xuống và cho biết
lớp trên cùng có 14 cột gỗ. Số hạng tổng quát dãy số
n
u
là
A.
14
n
un
. B.
13
n
un
.
C.
14 2
n
un
. D.
14 2 1
n
un
.
Hướng dẫn giải:
Đáp án đúng là: B.
Chồng gỗ là một cấp số cộng với
1
14u
và công sai
1d
.
Do đó
1
1 14 1 .1 13
n
u u n d n n
.
Câu 21: Cho cấp số cộng có số hạng đầu là 5, số hạng thứ 8 là 40. Khi đó công sai
của cấp số cộng đó bằng bao nhiêu?
A. 5. B. 6. C. 7. D. 2.
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
1
5u
và
81
81
40 5
8 1 . 40 5
77
uu
u u d d
.
Vậy công sai của cấp số cộng là 5.
Câu 22: Cho cấp số cộng
n
u
có
1
4u
và
5d
. Tổng 100 số hạng đầu tiên của
cấp số cộng
n
u
là
A. –24530. B. –24350. C. –23450. D. –32450.
Hướng dẫn giải:
Đáp án đúng là: B.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
19
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có:
100
100 2.4 99. 5
24350
2
S
.
Câu 23: Giá trị của
x
để ba số
6; ;20x
lập thành một cấp số cộng là
A.
12x
. B.
10x
. C.
15x
. D.
13x
.
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có
6; ;20x
lập thành một cấp số cộng khi và chỉ khi
6 20xx
2 26 13xx
.
Vậy
13x
.
Câu 24: Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?
A. 2; 4; 8; 16;…. B. 1; – 1 ; 1; – 1;… C. 1; 4; 9; 16;…. D. 1;
1
3
;
1
9
;
1
27
;….
Hướng dẫn giải:
Đáp án đúng là: C.
Xét dãy số
2 2 2
1 ;2 ;3 ;...
có:
23
12
49
4
14
uu
uu
nên
2 2 2
1 ;2 ;3 ;...
không phải là cấp số
nhân.
Câu 25: Cho cấp số nhân
n
u
với
3
45u
,
5
80u
. Giá trị của
4
u
là
A.
4
60u
. B.
4
50u
. C.
4
40u
. D.
4
55u
.
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có:
n
u
là cấp số nhân thì
2
54
4 5 3
43
.
uu
u u u
uu
2
44
45.80 3600 3600 60uu
.
Vậy
4
60u
.
Câu 26: Cho cấp số nhân
n
u
với
1
3u
và
2q
. Số 192 là số hạng thứ mấy của
cấp số nhân đã cho?
A. Số hạng thứ 5. B. Số hạng thứ 6.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
20
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C. Số hạng thứ 7. D. Số hạng thứ 9.
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có
1 1 6
1
1
. 3. 2 192 2 64 2 1 6 7
nn
n
n
u u q n n
.
Vậy 192 là số hạng thứ 7.
Câu 27: Cho cấp số nhân
n
u
có
1
0u
và
0q
. Với
1 km
, đẳng thức nào sau
đây là đúng?
A.
.
k
mk
u u q
. B.
.
m
mk
u u q
.
C.
.
mk
mk
u u q
. D.
.
mk
mk
u u q
.
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có
11
11
11
. . . .
km
k m k m
km
u u q u q q u q
hay
.
mk
mk
u u q
.
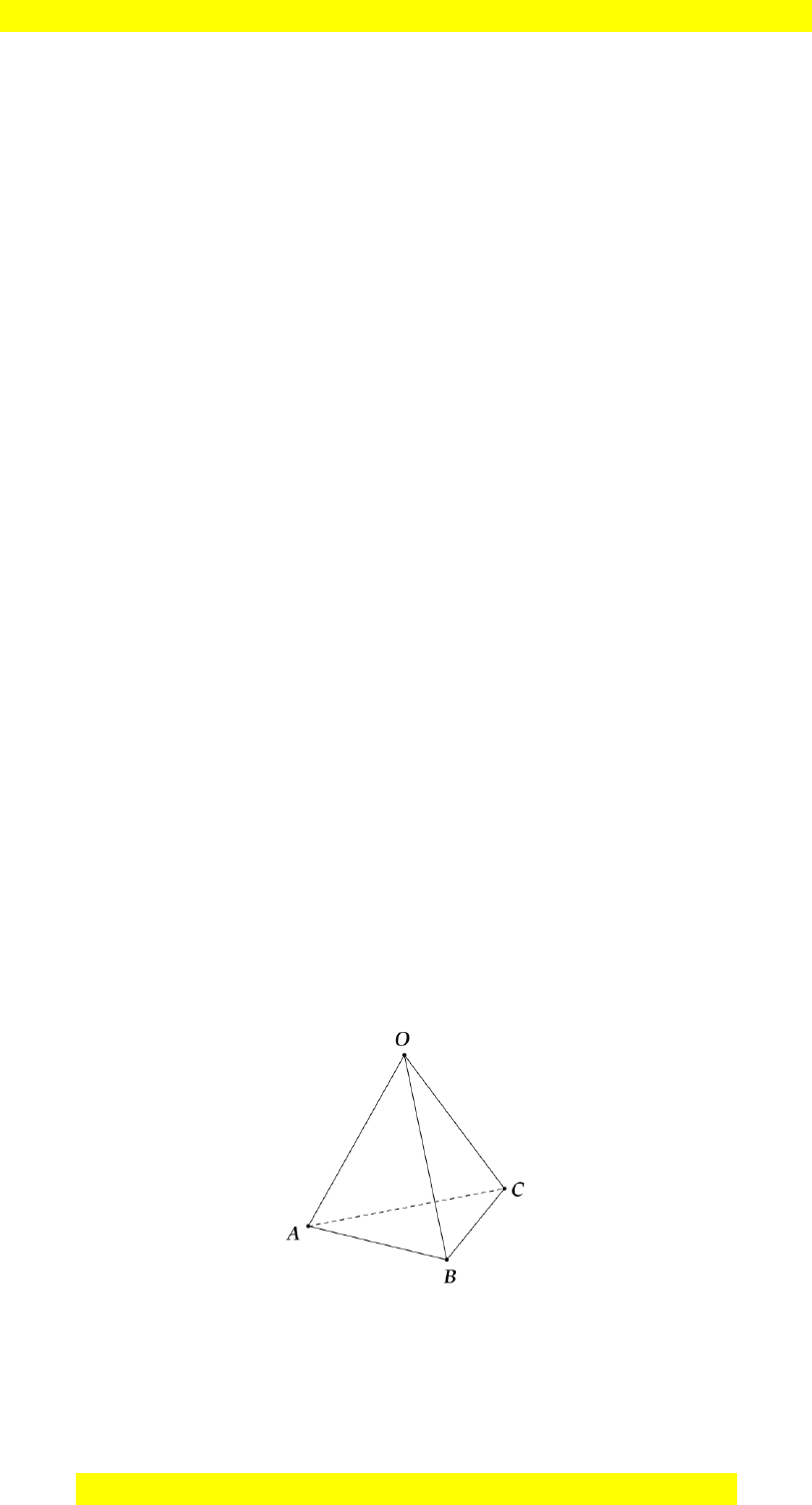
Câu 28: Cho tam giác
ABC
và một điểm
O
không thuộc mặt phẳng
ABC
. Giao
tuyến của hai mặt phẳng
OAB
và
ABC
là
A.
OA
. B.
AB
.
C.
BC
. D.
AC
.
Hướng dẫn giải:
Đáp án đúng là: B.
Vì
A OAB
và
A ABC
nên
A
là điểm chung giữa 2 mặt phẳng
OAB
và
ABC
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
21
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Tương tự,
B OAB
và
B ABC
nên
B
là điểm chung giữa 2 mặt phẳng
OAB
và
ABC
.
Do đó
AB
là giao tuyến chung giữa 2 mặt phẳng
OAB
và
ABC
.
Câu 29: Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm phân biệt. B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau. D. Bốn điểm phân biệt.
Hướng dẫn giải:
Đáp án đúng là: C.
A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng đi
qua ba điểm này.
B sai. Trong trường hợp điểm thuộc đường thẳng sẽ có vô số mặt phẳng đi qua điểm
và đường thẳng nào.
D sai. Bốn điểm không đồng phẳng sẽ không tạo được mặt phẳng nào chứa cả 4 điểm
đó.
Câu 30: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng có một điểm chung thì chúng có vô số điểm chung khác.
B. Hai đường thẳng song song khi và chỉ khi chúng không có điểm chung.
C. Hai đường thẳng song song khi và chỉ khi chúng không đồng phẳng.
D. Hai đường thẳng chéo nhau khi và chỉ khi chúng không đồng phẳng.
Hướng dẫn giải:
Đáp án đúng là: D.
A sai vì hai đường thẳng cắt nhau có 1 điểm chung duy nhất.
B và C sai vì hai đường thẳng song song khi và chỉ khi chúng đồng phẳng và không
có điểm chung.
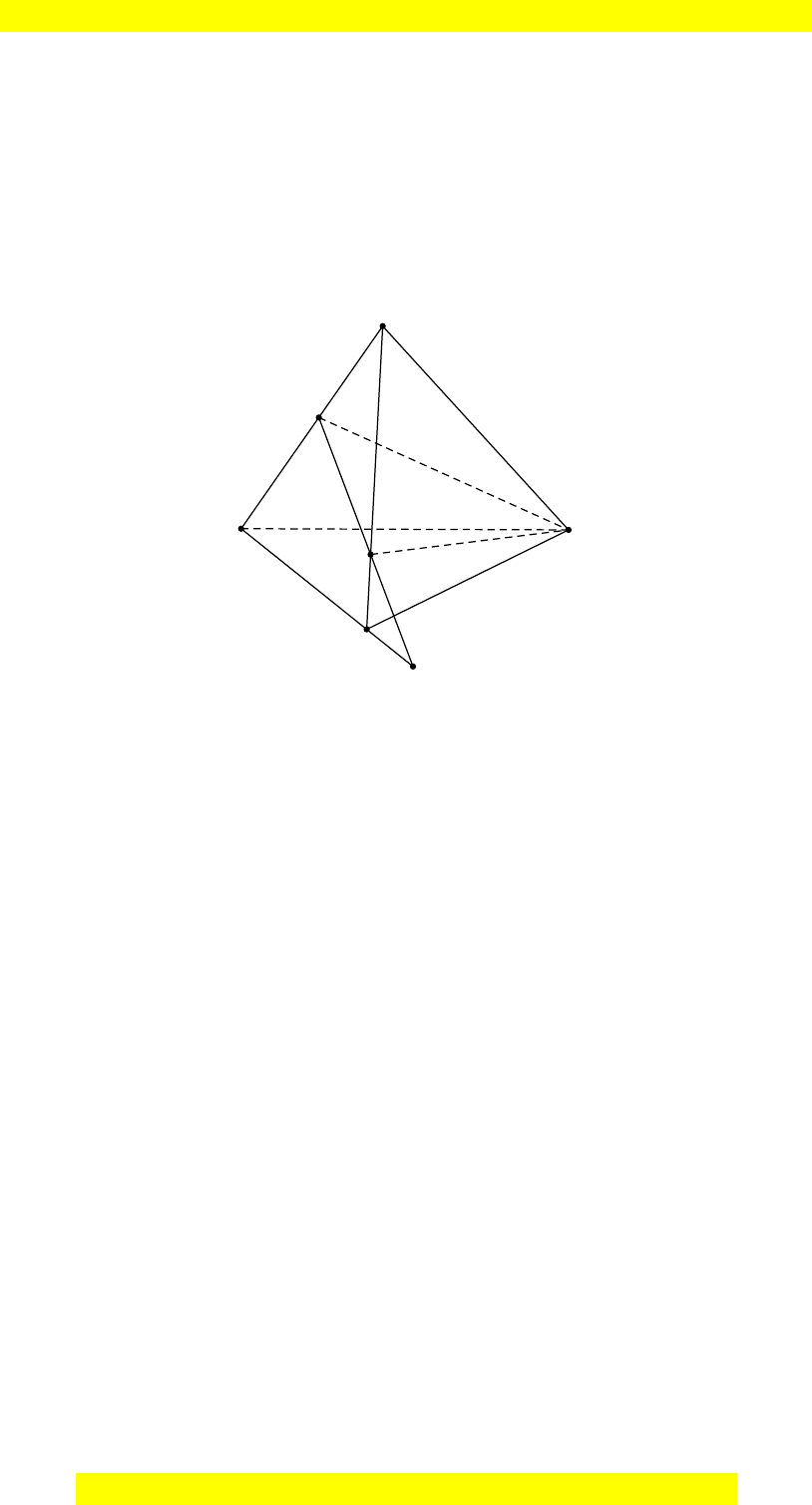
Câu 31: Cho điểm
A
không nằm trên mặt phẳng
chứa tam giác
BCD
. Lấy
,EF
là các điểm lần lượt nằm trên các cạnh
,AB AC
. Khi
EF
và
BC
cắt nhau tại
I
, thì
I
không phải là điểm chung của hai mặt phẳng nào sau đây?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
22
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
BCD
và
DEF
. B.
BCD
và
ABC
.
C.
BCD
và
AEF
. D.
BCD
và
ABD
.
Hướng dẫn giải:
Đáp án đúng là: D.
Điểm
I
là giao điểm của
EF
và
BC
mà
EF
nằm trên
DEF
,
ABC
và
AEF
nên điểm
I
sẽ là điểm chung giữa các cặp mặt phẳng
BCD
và
DEF
;
BCD
và
ABC
;
BCD
và
AEF
.
Câu 32: Cho hai đường thẳng chéo nhau
a
và
b
. Lấy
A
,
B
thuộc
a
và
C
,
D
thuộc
b
. Khẳng định nào sau đây là đúng khi nói về hai đường thẳng
AD
và
BC
?
A. Có thể song song hoặc cắt nhau. B. Cắt nhau.
C. Song song với nhau. D. Chéo nhau.
Hướng dẫn giải:
Đáp án đúng là: D.
F
A
B
C
D
E
I
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
23
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Theo giả thiết,
a
và
b
chéo nhau nên
a
và
b
không đồng phẳng.
Giả sử
AD
và
BC
đồng phẳng. Khi đó ta có 2 trường hợp:
,AD BC I I ABCD I a b
, mà
a
và
b
không đồng phẳng nên không
tồn tại điểm
I
.
//AD BC a
và
b
đồng phẳng. (mâu thuẫn với giả thiết).
Vậy điều giả sử là sai, do đó
AD
và
BC
chéo nhau.
Câu 33: Trong không gian, cho 3 đường thẳng
,,abc
. Biết
//ab
,
a
và
c
chéo nhau.
Khi đó hai đường thẳng
b
và
c
:
A. Trùng nhau hoặc chéo nhau. B. Cắt nhau hoặc chéo nhau.
C. Chéo nhau hoặc song song. D. Song song hoặc trùng nhau.
Hướng dẫn giải:
Đáp án đúng là: B.
Giả sử
//bc
thì ta có
//ac
(mâu thuẫn với giả thiết).
Do đó
b
và
c
cắt nhau hoặc chéo nhau.
Câu 34: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành. Gọi
d
là giao
tuyến của hai mặt phẳng
SAD
và
SBC
. Khẳng định nào sau đây là đúng?
A.
d
qua
S
và song song với
BC
. B.
d
qua
S
và song song với
DC
.
C.
d
qua
S
và song song với
AB
. D.
d
qua
S
và song song với
BD
.
Hướng dẫn giải:
Đáp án đúng là: A.
a
b
A
D
C
B
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
24
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có: Vì
//AD BC
, mà
AD
nằm trên
SAD
,
BC
nằm trên
SBC
nên giao tuyến
d
của 2 mặt phẳng sẽ song song với
AD
và
BC
.
Mặt khác,
S
là điểm chung giữa 2 mặt phẳng
SAD
và
SBC
nên
Sd
.
Vậy
d
qua
S
và song song với
BC
.
Câu 35: Cho tứ diện
ABCD
. Gọi
I
,
J
lần lượt là trọng tâm các tam giác
ABC
và
ABD
. Chọn khẳng định đúng trong các khẳng định sau:
A.
IJ
song song với
CD
. B.
IJ
song song với
AB
.
C.
IJ
song song với
BC
. D.
IJ
song song với
BD
.
Hướng dẫn giải:
Đáp án đúng là: A.
Gọi
,MN
lần lượt là trung điểm của
BC
và
BD
.
MN
là đường trung bình của tam giác
// 1BCD MN CD
.
d
A
D
C
B
S
J
I
N
M
A
B
C
D
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
25
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Mặt khác,
,IJ
lần lượt là trọng tâm của các tam giác
ABC
và
ABD
2
// 2
3
AI AJ
IJ MN
AM AN
.
Từ
1
và
2
suy ra
//IJ CD
.
III. Hướng dẫn giải tự luận
Câu 1: Giải các phương trình sau:
a)
sin cos 2
46
xx
;
b)
2
2cos 5sin 4 0xx
.
c)
3 sin cos 2sin2 3 0x x x
.
Hướng dẫn giải:
a)
sin cos 2
46
xx
sin cos 2
46
xx
5
sin cos 2
46
xx
5
sin sin 2
4 2 6
xx
sin sin 2
43
xx
22
43
,
22
43
x x k
k
x x k
32
12
,
4
22
43
xk
k
x x k
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
26
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
2
36 3
,
19
2
12
xk
k
xk
Vậy tập nghiệm của phương trình là:
2 19
;2
36 3 12
S k k k
.
b)
2
2cos 5sin 4 0xx
2
2 1 sin 5sin 4 0xx
2
2sin 5sin 2 0 1xx
Đặt
sinxt
, vì
1 sin 1x
nên
11t
. Khi đó, ta có:
2
1 2 5 2 0tt
2 1 2 0tt
1
t/m
2
2 k t/m
t
t
1
sin
2
x
22
66
,,
5
22
66
x k x k
kk
x k x k
Vậy tập nghiệm của phương trình là:
5
2 ; 2
66
S k k k
.
c)
3 sin cos 2sin2 3 0x x x
3 sin cos 4sin .cos 3 0x x x x
Đặt
sin cosx x t
, ta có:
sin cos 2sin
4
x x t x t
.
Vì
1 sin 1
4
x
nên
2 2sin 2
4
x
, hay
22t
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
27
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lại có:
2
22
sin cos sin cos 1 2sin .cosx x t x x t x x t
2
1
sin .cos
2
t
xx
.
Khi đó, phương trình
2
2
1
3 4 3 0 2 3 1 0
2
t
t t t
2 1 1 0tt
11
sin
22
1 sin 1
tx
tx
TH1:
2
1
6
sin ,
7
2
2
6
xk
xk
xk
.
TH2:
sin 1 2 ,
2
x x k k
.
Vậy tập nghiệm của phương trình là:
7
2 ; 2 ; 2 ;
6 2 6
S k k k k
.
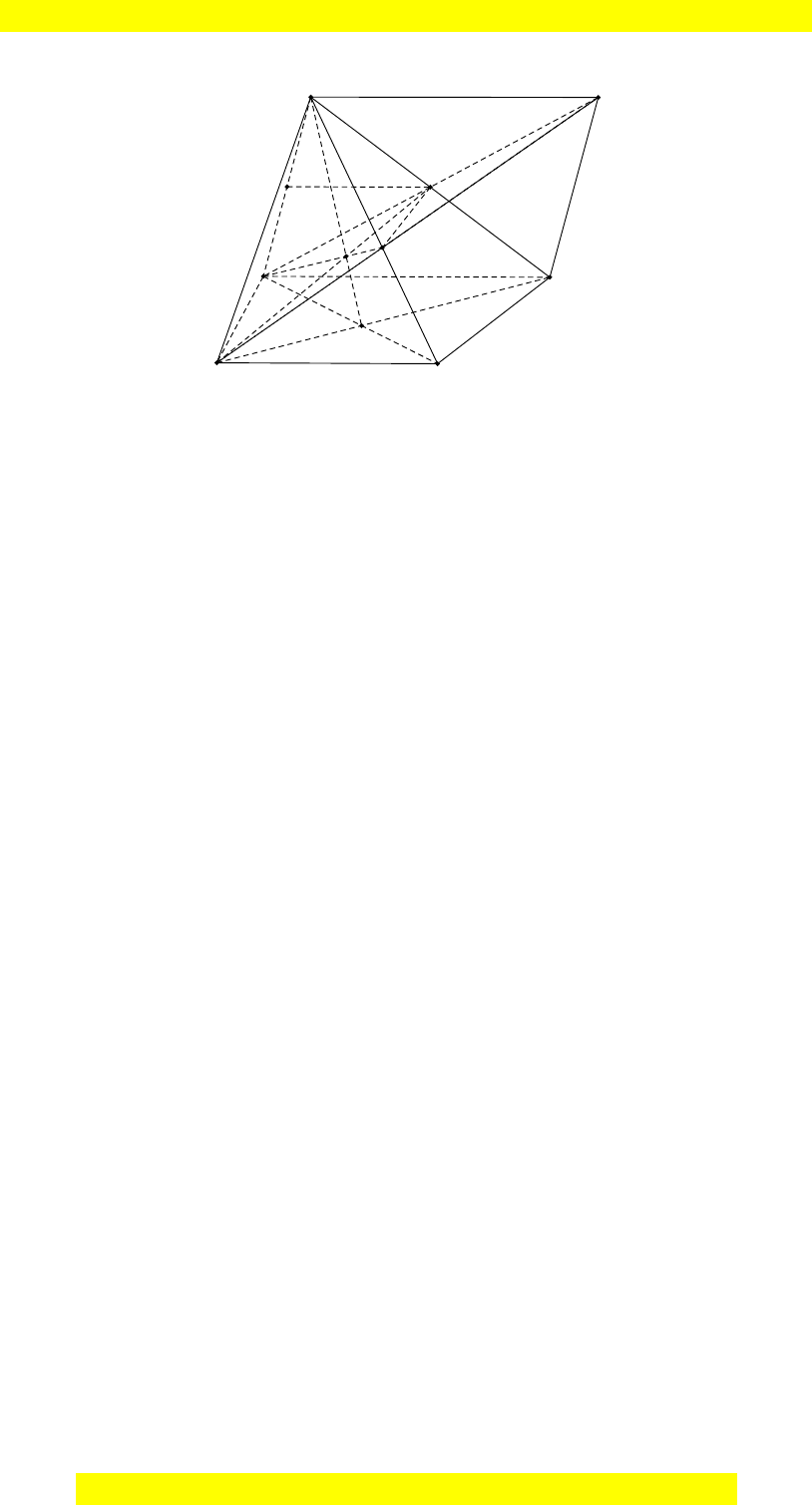
Câu 2: Cho hình chóp
.S ABCD
có đáy là hình thang đáy lớn là
AB
. Gọi
M
,
N
lần
lượt là trung điểm của
SA
và
SB
.
a) Chứng minh rằng:
//MN CD
.
b) Xác định giao tuyến của mặt phẳng
AND
với mặt phẳng
SAC
.
c) Gọi
P
là giao điểm giữa
SC
và mặt phẳng
AND
. Kéo dài
AN
và
DP
cắt nhau
tại
I
. Chứng minh rằng
// //SI AB CD
. Tứ giác
SIBA
là hình gì?
Hướng dẫn giải:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
28
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a) Vì
,MN
là các trung điểm của
SA
,
SB
nên
MN
là đường trung bình trong tam
giác
SAB
. Do đó
//MN AB
, mà
//AB CD
nên
//MN CD
. (đpcm)
b)
Gọi
O
là giao điểm của
AC
và
BD
,
J
là giao điểm của
SO
và
ND
. Ta có:
Vì
J SO
mà
SO
nằm trên
SAC
nên
J SAC
.
Mà
J ND
,
ND
nằm trên
AND
nên
J AND
.
Từ đó suy ra được
J
là điểm chung giữa mặt phẳng
AND
và mặt phẳng
SAC
.
Mặt khác
A SAC
,
A AND
, nên
A
là điểm chung giữa mặt phẳng
AND
và
mặt phẳng
SAC
.
AJ
là giao tuyến giữa mặt phẳng
AND
và mặt phẳng
SAC
.
c) Kéo dài
AJ
cắt
SC
tại
P
. Khi đó
P
là giao điểm giữa
SC
và mặt phẳng
AND
.
Ta có
I AN
mà
AN
nằm trên
SAB
nên
I SAB
.
I DP
mà
DP
nằm trên
SCD
nên
I SCD
.
I
là điểm chung giữa 2 mặt phẳng
SAB
và
SCD
.
SI
là giao tuyến giữa 2 mặt phẳng
SAB
và
SCD
.
Xét 3 mặt phẳng
SAB
,
SCD
và
ABCD
cắt nhau đôi một theo 3 giao tuyến
,SI AB
và
DC
nên theo định lí về ba đường giao tuyến, ta có
// //SI AB CD
hoặc
,,SI AB CD
đồng quy.
I
P
J
O
M
N
A
B
D
C
S
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
29
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Mà
//AB CD
nên
// //SI AB CD
.
Lại có:
//SI AB
nên theo định lí Talet, ta có:
SN IN SI
NB NA AB
.
Do
N
là trung điểm
SB
nên
SN NB
hay
11
SN SN IN SI
NB NB NA AB
SI AB
.
Tứ giác
SIBA
có
//SI AB
SI AB
tứ giác
SIBA
là hình bình hành.
Câu 3: Cho dãy số
n
u
với
n
an b
u
cn d
với
, , ,a b c d
là các số thực và
0cn d
với mọi
*
n
.
a) Chứng minh rằng: Nếu
0ad bc
thì
n
u
là một dãy tăng, còn
0ad bc
thì
n
u
là một dãy giảm và khi
0ad bc
thì
n
u
là một dãy không thay đổi, tức là
12
...
n
u u u
.
b) Tính giá trị của các số hạng trong dãy khi dãy
n
u
là dãy không thay đổi.
Hướng dẫn giải:
a) Xét
n
u
với
n
an b
u
cn d
, ta có:
1
1
1
nn
a n b an a b
an b an b
uu
c n d cn d cn c d cn d
an a b cn d cn c d an b
cn d cn c d
22
acn ad ac bc n d a b acn n bc ac ad b c d
cn d cn c d
ad bc
cn d cn c d
Vì
,cd
là các số thực thoả mãn
*
0,cn d n
nên
0cn d cn c d
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
30
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó, ta có các trường hợp sau:
Khi
0ad bc
thì
*
11
0,
n n n n
ad bc
u u u u n
cn d cn c d
, hay
n
u
là dãy tăng.
Khi
0ad bc
thì
*
11
0,
n n n n
ad bc
u u u u n
cn d cn c d
, hay
n
u
là dãy giảm.
Khi
0ad bc
thì
*
11
0,
n n n n
ad bc
u u u u n
cn d cn c d
.
Vậy
1 2 3
...
n
u u u u
, hay
n
u
là một dãy không thay đổi.
b)
0
ab
ad bc ad bc
cd
. Đặt
0
a ct
ab
tt
b dt
cd
.
Khi đó
.
n
t cn d
an b ct n dt
ut
cn d cn d cn d
hay
n
a
u
c
.
Vậy
n
a
u
c
với mọi
*
n
.
Nhắn tin Zalo