Đề thi HSG Toán 11 Trường THPT Chuyên Bắc Ninh

HỘI CÁC TRƯỜNG THPT CHUYÊN
ĐỀ THI CHỌN HSG GIỎI LẦN THỨ XV
KHU VỰC DUYÊN HẢI, ĐỒNG BẰNG BẮC BỘ
MÔN THI: TOÁN – KHỐI 11
TRƯỜNG THPT CHUYÊN BẮC NINH
Thời gian làm bài 180 phút ĐỀ THI ĐỀ XUẤT
(Đề này có 5 câu; gồm 01 trang)
Câu 1. (4,0 điểm) Cho dãy số được xác định bởi và với mọi
a) Tìm công thức số hạng tổng quát của dãy số b) Tính
Câu 2. (4,0 điểm) Tìm tất cả các đa thức
với hệ số thực thỏa mãn với thỏa mãn
Câu 3: (4,0 điểm) Cho tam giác
nhọn nội tiếp đường tròn tâm và có đường cao đồng quy tại . cắt
tại . Đường tròn ngoại tiếp tam giác cắt tại khác . cắt tại . là trung điểm của
. là điểm đối xứng với qua . là hình chiếu của trên . Trên lấy điểm sao cho vuông góc với .
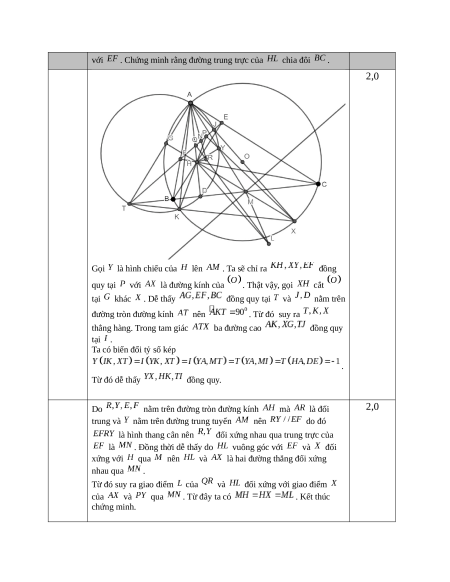
Chứng minh rằng đường trung trực của chia đôi .
Câu 4: (4,0 điểm) Tìm tất cả các số nguyên dương sao cho là ước của .
Câu 5: (4,0 điểm) Cho tập hợp gồm
số nguyên dương sao cho tồn tại một
cách chia chúng thành cặp mà tích mỗi số cùng cặp thì không chính phương. Hỏi
có ít nhất bao nhiêu cách chia như thế đối với ? Hai cách chia được gọi là khác
nhau nếu có hai số cùng cặp trong cách chia này nhưng lại không cùng cặp trong cách chia khác.
TRƯỜNG THPT CHUYÊN BẮC HƯỚNG DẪN CHẤM ĐỀ THI CHỌN HỌC SINH NINH GIỎI
CỤM DUYÊN HẢI ĐỒNG BẰNG BẮC BỘ LẦN
MÔN THI: TOÁN - LỚP 11 Câu Nội dung Điểm 1 Cho dãy số được xác định bởi 4,0 và với mọi
a) Tìm công thức số hạng tổng quát của dãy số b) Tính a) Từ gt ta có 2,0 Đặt là cấp số nhân có , công bội Vậy 2,0 b) Ta có Ta có Mà với n đủ lớn, và nên suy ra 2
Tìm tất cả các đa thức
với hệ số thực thỏa mãn 4,0 với thỏa mãn Nhận thấy bộ thỏa mãn đk Do đó 4,0 thay vào gt ta đc Giả sử thay vào (2) ta được Giải (3) ta được và Bởi vậy
Thử lại thấy thỏa mãn. Vậy tất cả các đa thức cần tìm là (với là các hằng số bất kì). 3 Cho tam giác
nhọn nội tiếp đường tròn tâm và có đường cao đồng quy tại . cắt
tại . Đường tròn ngoại tiếp tam giác cắt tại khác . cắt tại . là trung điểm của
. là điểm đối xứng với qua . là hình chiếu của trên . Trên lấy điểm sao cho vuông góc