Đề thi thử vào lớp 10 môn Toán năm 2025-2026

UBND PHƯƠNG ĐÔNG ĐA
ĐỀ KHAO SAT CHÂT LƯƠNG THANG 9
TRƯƠNG THCS THINH QUANG
NĂM HỌC: 2025 – 2026 Ngay thi: 03/12/2025 Thời gian: 120 phút
Bai I. (1,0 điểm) Tính giá trị của biểu thức
1) A  8  2 18  3 32 2) B     2 2 3 6 1 3  3 1 2
Bai II. (1,5 điểm) Cho hai biểu thức 2 x 3  A  và x 5 8 x 6 B   
với x  0, x 1 x 1 x 1 x 1 x 1
1) Tính giá trị biểu thức A khi x  9
2) Rút gọn biểu thức B
3) Tìm giá trị của x để P  .
A B đạt giá trị nguyên lớn nhất
Bai III. (1,5 điểm)
1) Giải phương trình sau : a) 3 x  2 5  4 x  5 b)
4x  20  4 x  5  8 16 64 2) Toán xác suất
Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi
đó các số 1,2,3,. .,20; hai viên bi khác nhau thì viết hai số khác nhau.
Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”. Tính xác suất biến cố : “Số xuất hiện
trên viên bi được lấy ta chia 7 dư 1”
Bai IV. (2,0 điểm).
1) Hai người thợ quét sơn một ngôi nhà. Nếu họ cùng làm trong 6 ngày thì xong công việc. Hai
người làm cùng nhau trong 3 ngày thì người thứ nhất được chuyển đi làm công việc khác,
người thứ hai làm một mình trong 4 ngày nữa thì hoàn thành công việc. Hỏi nếu làm riêng thì
mỗi người hoàn thành công việc đó trong bao lâu?
2) Bạn Mai làm một bài thi Toán gồm 30 câu trắc nghiệm, mỗi câu đúng được cộng 4 điểm,
mỗi câu sai bị trừ 1 điểm, câu nào không làm thì không bị trừ và cũng không được cộng điểm.
Bạn Mai đã làm 25 câu và đạt hơn 82 điểm. Hãy cho biết bạn Mai cần trả lời ít nhất bao nhiêu
câu hỏi đúng để đạt được số điểm trên?
Bai V (3,5 điểm)
1) Tính diện tích phần viên trắng men xanh của đĩa sứ trong hình vẽ bên
(kết quả làm tròn đến phần nguyên   3,14 ). 2) Cho đường tròn ( ;
O R) và điểm A nằm ngoài đường tròn. Qua A kẻ
đường thẳng d  OA . Lấy điểm M bất kì trên d ( M là tiếp điểm). Kẻ
tiếp tuyến MB với đường tròn (O) ( B là tiếp điểm).
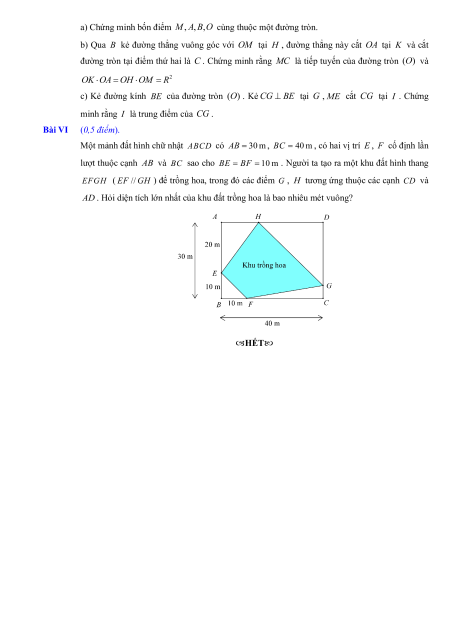
a) Chứng minh bốn điểm M, ,
A B,O cùng thuộc một đường tròn.
b) Qua B kẻ đường thẳng vuông góc với OM tại H , đường thẳng này cắt OA tại K và cắt
đường tròn tại điểm thứ hai là C . Chứng minh rằng MC là tiếp tuyến của đường tròn (O) và 2
OK OA  OH OM  R
c) Kẻ đường kính BE của đường tròn (O) . Kẻ CG  BE tại G , ME cắt CG tại I . Chứng
minh rằng I là trung điểm của CG .
Bai VI (0,5 điểm).
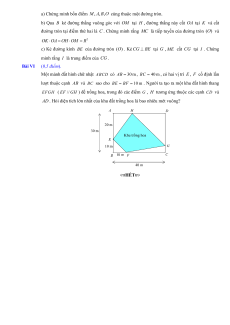
Một mảnh đất hình chữ nhật ABCD có AB  30m , BC  40 m , có hai vị trí E , F cố định lần
lượt thuộc cạnh AB và BC sao cho BE  BF  10 m . Người ta tạo ra một khu đất hình thang
EFGH ( EF // GH ) để trồng hoa, trong đó các điểm G , H tương ứng thuộc các cạnh CD và
AD . Hỏi diện tích lớn nhất của khu đất trồng hoa là bao nhiêu mét vuông? HẾT
UBND PHƯƠNG ĐÔNG ĐA HƯƠNG DÂN GIAI
TRƯƠNG THCS THINH QUANG
ĐỀ KHAO SAT CHÂT LƯƠNG THANG 9 ĐỀ CHINH THƯC
NĂM HỌC: 2025 – 2026
Bai I. (1,0 điểm) Tính giá trị của biểu thức
1) A  8  2 18  3 32 2) B     2 2 3 6 1 3  3 1 2 Lời giải
1) A  8  2 18  3 32  2 2  2.3 2  3.4 2  2 2  6 2 12 2  4 2 2) B 2 2     2 2 3 6 1 3    3 13 3  1 2 3 3 1 2 3 1 3 1 2 3 1  
 3 11 2 3   3     1 2 3 3 1 3 1
Bai II. (1,5 điểm) Cho hai biểu thức 2 x 3  A  và x 5 8 x 6 B   
với x  0, x 1 x 1 x 1 x 1 x 1
1) Tính giá trị biểu thức A khi x  9
2) Rút gọn biểu thức B
3) Tìm giá trị của x để P  .
A B đạt giá trị nguyên lớn nhất Lời giải
1) Khi x  9tm giá trị biểu thức A là : 2. 9 3  A  6 3  3  9 1 31 2 Vậy 3
A  khi x  9 2 x  x   1 5 x 1 2) x 5 8 x 6  B    8 x 6    x 1 x 1 x 1
 x  1 x 1  x 1 x 1  x 1 x 1 2
x  x  5 x  5 8 x  6    x  1 x 1  x 2 x 1     x   1  x 1
 x  1 x 1  x  1 x  1 x 1 2 x   1 5 3)    5 P
2 x 3 x 1 2 x 3  . A B  .    2  x 1 x 1 x 1 x 1 x 1 +) Với  x 5 5
 0 ta có x 1  0   0  2   2  P  2 (1) x 1 x 1 +) Với  x 5 5
 0 ta có x 11   5  2   3   P  3 (2) x 1 x 1
Từ (1) và (2) ta có  3  P  2 , mà P , P a m x nên P1 5 2 5   1 
1  x 1 5  x 16tm x 1 x 1
Vậy x 16 là giá trị cần tìm.
Bai III. (1,5 điểm)
3) Giải phương trình sau : c) 3 x  2 5  4 x  5 d)
4x  20  4 x 5  8 16 64 4) Toán xác suất
Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi
đó các số 1,2,3,. .,20; hai viên bi khác nhau thì viết hai số khác nhau.
Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”. Tính xác suất biến cố : “Số xuất hiện
trên viên bi được lấy ta chia 7 dư 1”. Lời giải
1) Giải phương trình sau :
a) 3 x  2 5  4 Đk : x  2 3 x  2  9 x  2  3 x  2  9 x 11tm
Vậy x 11 là nghiệm của phương trình. x  5 b)
4x  20  4 x 5  8 16 ĐK. x  5 64 1
2 x 5  4 x 5 16. x 5  8 8 4 x 5  8 x  5  2 x  9tm
Vậy x  9 là nghiệm của phương trình. 2) +) Có 20 kết quả
Xét biến cố : “Số xuất hiện trên viên bi được lấy ta chia 7 dư 1”
+) Có 3 kết quả thuận lợi cho biến cố là 1;8;15
+) Xác suất của biến cố là 3 20
Bai IV. (2,0 điểm).