Giáo án Giới hạn của dãy số Toán 11 Chân trời sáng tạo

Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) Ngày so n ạ : .../.../... Ngày d y ạ : .../.../... CHƯƠNG III: GI I Ớ H N Ạ . HÀM S Ố LIÊN T C Ụ BÀI 1: GI I Ớ H N Ạ C A Ủ DÃY S Ố (2 TI T) Ế I. MỤC TIÊU: 1. Ki n ế th c
ứ , kĩ năng: H c ọ xong bài này, HS đ t ạ các yêu c u ầ sau: - Nh n ậ bi t ế đ c ượ khái ni m ệ gi i ớ h n ạ c a ủ dãy s . ố - Gi i ả thích đ c ượ m t ộ s ố gi i ớ h n ạ c ơ b n ả nh : ư
lim 1 =0(k ∈N¿),lim qn=0(¿q∨¿1) và lim ⁡c=c v i ớ c là h n ằ g s . ố nk - V n ậ d n ụ g đ c ượ các gi i ớ h n ạ c ơ b n ả và các phép toán gi i ớ h n ạ dãy s ố đ ể tìm gi i ớ h n ạ c a ủ m t ộ s ố dãy s ố đ n ơ gi n ả . - Tính đ c ượ t n ổ g c a ủ m t ộ c p ấ s ố nhân lùi vô h n ạ và v n ậ d n ụ g đ c ượ k t ế qu ả đó đ ể gi i ả quy t ế m t ộ s ố tình hu n ố g th c ự ti n ễ gi ả đ n ị h ho c ặ liên quan đ n ế th c ự ti n ễ . 2. Năng l c ự Năng l c ự chung: - Năng l c ự t ự ch ủ và t ự h c ọ trong tìm tòi khám phá - Năng l c ự giao ti p ế và h p
ợ tác trong trình bày, th o ả lu n ậ và làm vi c ệ nhóm - Năng l c ự gi i ả quy t ế v n ấ đ ề và sáng t o ạ trong th c ự hành, v n ậ d n ụ g. Năng l c ự riêng: - Năng l c ự t ư duy và l p ậ lu n ậ toán h c
ọ : so sánh, phân tích, l p ậ lu n ậ trong quá
trình khám phá, hình thành ki n ế th c ứ (gi i ớ h n ạ h u ữ h n ạ c a ủ dãy s , ố các phép toán v ề gi i ớ h n ạ hũu h n ạ c a ủ dãy s , ố ...). - Năng l c ự giao ti p ế toán h c ọ : s ử d n ụ g các thu t ậ ng , ữ khái ni m, ệ công th c, ứ kí hiệu toán h c ọ trong trình bày, th o ả lu n ậ , làm vi c ệ nhóm. - Gi i ả quy t ế v n ấ đ ề toán h c ọ : th c ự hành và v n ậ d n ụ g ki n ế th c ứ đ ể tìm gi i ớ h n ạ dãy số. - S ử d n ụ g công c , ụ ph n ươ g ti n ệ h c ọ toán. M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) 3. Ph m ẩ ch t ấ - Có⁡ý th c ứ h c ọ t p ậ , ý th c
ứ tìm tòi, khám phá và sáng tạo, có ý th c ứ làm vi c ệ nhóm, tôn tr n ọ g ý ki n ế các thành viên khi h p ợ tác. - Chăm chỉ tích c c ự xây d n ự g bài, có trách nhi m, ệ chủ đ n ộ g chi m ế lĩnh ki n ế th c ứ theo s ự h n ướ g d n ẫ c a ủ GV. II. THI T Ế B Ị D Y Ạ H C Ọ VÀ H C Ọ LI U Ệ 1. Đ i ố v i ớ GV: SGK, Tài li u ệ gi n ả g d y ạ , giáo án, đ ồ dùng d y ạ h c. ọ 2. Đ i ố v i
ớ HS: SGK, SBT, vở ghi, gi y ấ nháp, đồ dùng h c ọ t p ậ (bút, th c. ướ ..), b n ả g nhóm, bút vi t ế b n ả g nhóm. III. TI N Ế TRÌNH D Y Ạ H C Ọ A. HOẠT ĐỘNG KH I Ở Đ N Ộ G (M Ở Đ U Ầ ) a) M c ụ tiêu: - T o ạ h n
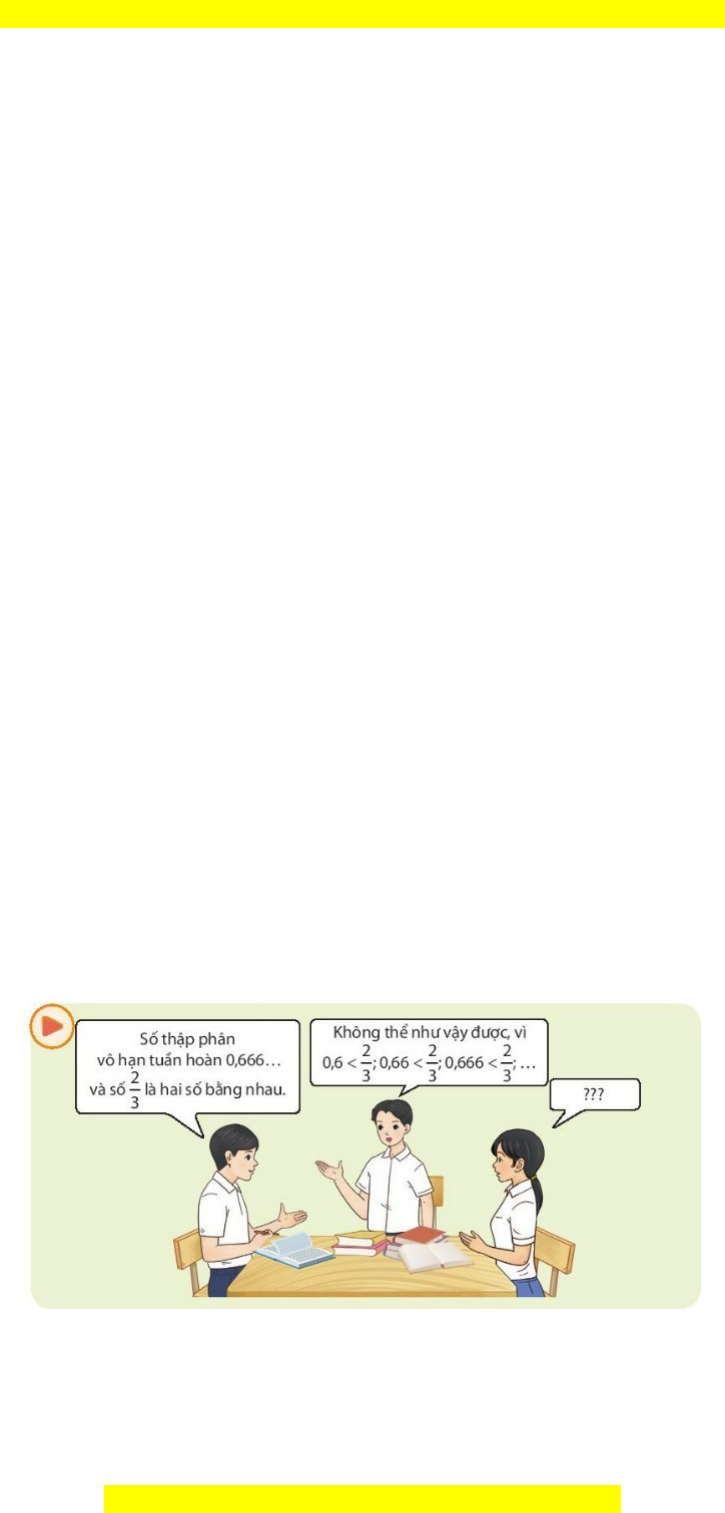
ứ g thú, thu hút HS tìm hi u ể n i ộ dung bài h c. ọ b) N i ộ dung: HS đ c ọ tình hu n ố g m ở đ u ầ , suy nghĩ tr ả l i ờ câu h i ỏ .
c) Sản phẩm: HS trả l i ờ đ c ượ câu h i ỏ m ở đ u ầ , b c ướ đ u ầ hình dung v ề n i ộ dung bài h c. ọ d) T ổ ch c ứ th c ự hi n: ệ Bư c ớ 1: Chuy n ể giao nhi m ệ v : ụ - GV yêu c u ầ HS đ c ọ tình hu n ố g m ở đ u ầ : - GV đ t ặ câu h i ỏ g i ợ m : ở +⁡Nh c⁡ ắ l i ạ ⁡khái⁡ni m ệ ⁡s ⁡ ố th p
ậ ⁡phân⁡vô⁡h n ạ ⁡tu n ầ ⁡hoàn? M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) ⁡(Số th p ậ phân vô h n ạ tu n ầ hoàn: Trong ph n ầ th p ậ phân, b t ắ đ u ầ t ừ m t ộ hàng nào đó, có m t ộ ch ữ s ố hay m t ộ c m ụ ch ữ s ố li n ề nhau xu t ấ hi n ệ liên ti p ế mãi). +⁡Theo⁡em⁡b n
ạ ⁡nào⁡nói⁡đúng?⁡T i ạ ⁡sao? Bư c ớ 2: Th c ự hi n ệ nhi m ệ v :
ụ HS quan sát và chú ý l n ắ g nghe, th o ả lu n ậ nhóm đôi hoàn thành yêu c u ầ . Bư c ớ 3: Báo cáo, th o ả lu n: ậ GV g i ọ m t ộ s ố HS tr ả l i ờ , HS khác nh n ậ xét, b ổ sung. Bư c ớ 4: K t ế lu n, ậ nh n ậ đ nh: ị GV đánh giá k t ế qu ả c a ủ HS, trên c ơ s ở đó d n ẫ d t ắ HS vào bài h c ọ m i ớ : “Trong ch n ươ g này, chúng ta s ẽ tìm hi u ể v ề m t ộ phép toán m i ớ : phép toán gi i ớ h n
ạ . Nhờ phép toán này, ng i ườ ta xây d n ự g nên nh n ữ g khái ni m ệ cơ b n ả c a ủ Gi i ả tích toán h c ọ như tính liên t c, ụ đ o ạ hàm và tích phân. N i ộ dung c a ủ ch n ươ g này g m: ồ gi i ớ h n ạ c a ủ dãy s , ố gi i ớ h n ạ c a ủ hàm s ố và tính liên t c ụ c a ủ hàm s .
ố Để tìm đáp án chính xác cho câu h i
ỏ trên, chúng ta vào bài h c ọ tìm hi u ể v ề gi i ớ h n ạ c a ủ hàm s . ố ” Bài m i ớ : Gi i ớ h n ạ c a ủ dãy s . ố
B. HÌNH THÀNH KI N Ế TH C Ứ M I Ớ Ho t ạ đ ng ộ 1: Gi i ớ h n ạ h u ữ h n ạ c a ủ dãy s . ố a) M c ụ tiêu: - HS nh n ậ bi t ế đ c ượ khái ni m ệ gi i ớ h n ạ 0 và gi i ớ h n ạ h u ữ h n ạ c a ủ dãy s . ố lim 1 - Gi i ả thích đ c ượ m t ộ s ố gi i ớ h n ạ c ơ b n ả nh : ư
=0 (k ∈ N ¿) , lim qn=0(¿ q∨¿1) nk
và lim ⁡c=c v i ớ c là h n ằ g s . ố - HS v n ậ d n ụ g đ c ượ các gi i ớ h n ạ c ơ b n ả và các phép toán gi i ớ h n ạ dãy s ố đ ể tìm gi i ớ h n ạ c a ủ m t ộ s ố dãy s . ố b) N i ộ dung: HS đ c ọ SGK, nghe gi n ả g, th c ự hi n ệ các nhi m ệ vụ đ c ượ giao, suy nghĩ tr ả l i ờ câu h i ỏ , th c ự hi n ệ các ho t ạ đ n ộ g HĐKP 1, 2, Th c ự hành 1, 2, đ c ọ hi u ể Ví d . ụ c) Sản ph m
ẩ : HS hình thành đ c ượ ki n ế th c ứ bài h c ọ , câu tr ả l i ờ c a ủ HS cho các câu h i ỏ . HS trả l i ờ các câu h i ỏ v ề dãy s ố đ ể hình thành khái ni m ệ gi i ớ h n ạ h u ữ h n ạ c a ủ dãy số; áp d n ụ g các gi i ớ h n ạ c ơ b n ả đ ể tìm gi i ớ h n ạ c a ủ dãy s . ố M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85
Đây là bản xem th , vu ử i lòng mua tài li u ệ đ xe ể m chi ti t ế (có l i ờ gi i ả ) d) T ổ ch c ứ th c ự hi n: ệ HĐ CỦA GV VÀ HS SẢN PHẨM D Ự KI N Ế Bư c ớ 1: Chuy n ể giao nhi m ệ 1. Gi i ớ h n ạ h u ữ h n ạ c a ủ dãy s . ố v : ụ a) Gi i ớ h n ạ 0 c a ủ dãy số - GV yêu c u ầ HS th o ả lu n ậ n −1¿ ¿
nhóm đôi, hoàn thành HĐKP 1. HĐKP 1: . ¿ un=¿ + Quan sát vào công th c ứ c a ủ a) dãy số và giá trị c a ủ b n ả g a, ta thấy khi n càng l n ớ thì giá trị n 10 20 50 100 1000 phân s ố càng nh . ỏ |un| 0,1 0,05 0,02 0,01 0,0001 + Quan sát hình v ẽ đi m ể u 1 n b) |un|= . n càng d n ầ đ n ế đi m ể 0 khi n tr ở 1 nên r t ấ l n ớ . Hay chính là v i ớ s ố Ta có: <0,01 khi n n >100 ; d n ươ g bất kì cho tr c, ướ |u 1 n| <0,001 khi n n >1000 . v n ẫ nh ỏ h n ơ s ố đó, k ể t ừ s ố c) hàng nào đó tr ở đi. Ví d ụ cho s ố d n ươ g M = 0,002; thì v i ớ n > 2000 thì 1 Kho n ả g cách từ u ế ở ấ |u n đ n 0 tr nên r t bé khi n n|= <0,002. n tr ở nên r t ấ l n ớ . → Ta g i ọ đó dãy có gi i ớ h n ạ Kết lu n ậ là 0. Ta nói dãy s ố (un) có gi i ớ h n ạ 0 khi n d n ầ t i ớ d n ươ g vô c c ự , n u ế |un| nh ỏ h n ơ m t ộ s ố - GV cho HS nêu l i ạ khái ni m ệ d n ươ g b t ấ kì cho tr c, ướ k ể t ừ m t ộ s ố h n ạ g nào v ề dãy s ố có gi i ớ h n ạ 0. đó tr ở đi, kí hi u
ệ lim un=0 hay u →0 khi n → n +∞
n →+∞ . Ta còn vi t ế là lim ⁡un=0 . Ví d ụ 1 (SGK – tr.64) - GV cho HS tìm hi u ể Ví dụ 1. M i
ọ thắc mắc vui lòng xin vui lòng: 084 283 45 85