5 Đề thi ĐGNL ĐHSP Hà Nội môn Toán (có lời giải)

ĐỀ SỐ 1
A. TÔ TRÊN PHIẾU TRẢ LỜI TRẮC NGHIỆM
Phần I (4 điểm). Thí sinh trả lời từ câu 1 đến câu 16. Đối với mỗi câu, thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y  f x có đạo hàm f x  x  2x   1 , x
  . Mệnh đề nào dưới đây đúng?
A. Hàm số đã cho đồng biến trên 1;.
B. Hàm số đã cho đồng biến trên ;2 .
C. Hàm số đã cho nghịch biến trên 2;  1 .
D. Hàm số đã cho nghịch biến trên 1;2 .
Câu 2. Tập nghiệm của bất phương trình log  2 x  2  3 là 3 
A. S  ; 55;  . B. S   . C. S  .
D. S  5;5 . 2
Câu 3. Đường tiệm cận xiên của đồ thị hàm số  
f x 2x 3x 1  có phương trình là: x 1
A. y  2x  5 .
B. y  2x  5.
C. y  2x  3 .
D. y  2x  3 .
Câu 4. Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong một tuần ở bảng sau: Thời gian
0;60 60;120 120;180 180;240 240;300 300;360 (đơn vị: giây) Số cuộc gọi 9 9 5 7 2 1
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên bằng: A. 180. B. 140. C. 60 . D. 169. 2 2 Câu 5. Nếu f
 xdx  5 thì 4 f
 xdx bằng 1  1  A. 20 . B. 10. C. 5 . D. 5 . 2 4
Câu 6. Cho cấp số nhân u có số hạng đầu u  7 và công bội q  3 . Khi đó số hạng thứ hai của cấp số n  1 nhân đã cho là: A. u  21. B. u 10 . C. u  49 . D. u  343 . 2 2 2 2 Câu 7. Cho ,
A B là hai biến cố độc lập với P A  0,2024;P B   0,2025 . Kết quả PB | A bằng A. 0,4049 . B. 0,7975. C. 0,2025 . D. 0,2024 .
Câu 8. Cho hình tứ diện ABCD . Gọi G là trọng tâm của tam giác BCD. Mệnh đề nào sau đây đúng?
   
   
A. AB  AC  AD  3AG .
B. AB  CD  AD  AD .
   
   
C. AB  AC  AD  3AG .D. BC  AD  AC  AC .
Câu 9. Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x  y  z 8x  2y 1  0 . Tọa độ tâm và bán kính
mặt cầu S  lần lượt là
A. I 4;1;0, R  2 .
B. I 4;1;0, R  4 . C. I 4; 1  ;0, R  2 . D. I 4; 1  ;0, R  4 .
Câu 10. Khi cắt một vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ,  3  x  3,
mặt cắt là hình vuông có độ dài các cạnh là 2
3 x . Thể tích của vật thể đã cho bằng A. 3 . B. 4 3 . C. 4 3 . D.  3 .
Câu 11. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình? A. x  2   y  . B. x 2 y  . C. 2x 1 y  . D. 3
y  x  3x  2. x 1 x 1 x 1
Câu 12. Tất cả các nghiệm của phương trình   2cos x    2    0 là  4  A.  
x  k2; x    k2 k   .
B. x  k; x    k k  . 2 2 C.  
x  k; x    k2 k   .
D. x  k2; x    k k   . 2 2 
Câu 13. Trong không gian Oxyz , mặt phẳng nào dưới đây có vectơ pháp tuyến n  1;2;3 ?
A. 2x  4y  6z 1  0 . B. x  2y  3z  2  0 . C. x  2z  3  0.
D. x  2y  3  0 .
Câu 14. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a . Cạnh bên SC vuông góc với mặt phẳng
ABC, SC  a . Thể tích khối chóp S.ABC bằng 3 3 3 3 A. a 3 . B. a 2 . C. a 3 . D. a 3 . 3 12 9 12
Câu 15. Diện tích hình phẳng giới hạn bởi đồ thị hàm số x
y  e , trục hoành và hai đường thẳng x  0 và x  3 bằng A. 3 e . B. 3 e 1. C. 2 e 1. D. e 2 e   1 .
Câu 16. Một hộp đựng 6 bi xanh đánh số từ 1 đến 6 , 7 bi vàng đánh số từ 1 đến 7 và 8 bi đỏ đánh số
từ 1 đến 8 . Lấy ngẫu nhiên 3 bi từ hộp. Xác suất để ba bi lấy được có 3 số khác nhau và khác màu là A. 108 . B. 108 . C. 116 . D. 109 . 775 665 565 785
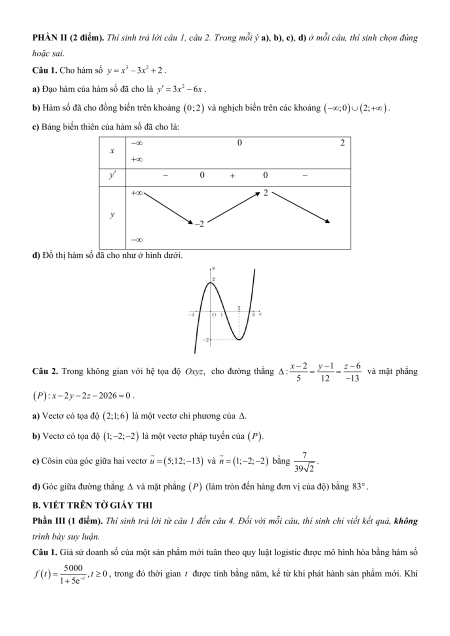
PHẦN II (2 điểm). Thí sinh trả lời câu 1, câu 2. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số 3 2
y  x – 3x  2 .
a) Đạo hàm của hàm số đã cho là 2
y  3x  6x .
b) Hàm số đã cho đồng biến trên khoảng 0;2 và nghịch biến trên các khoảng ;0 2; .
c) Bảng biến thiên của hàm số đã cho là:  0 2 x  y  0  0   2 y 2  
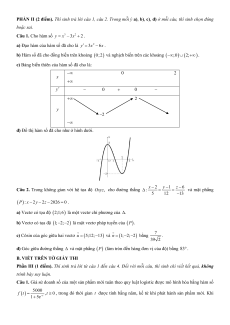
d) Đồ thị hàm số đã cho như ở hình dưới.
Câu 2. Trong không gian với hệ tọa độ   
Oxyz, cho đường thẳng
x 2 y 1 z 6  :   và mặt phẳng 5 12 1  3
P: x  2y  2z  2026  0 .
a) Vectơ có tọa độ 2;1;6 là một vectơ chỉ phương của . 
b) Vectơ có tọa độ 1; 2  ; 2
  là một vectơ pháp tuyến của P.  
c) Côsin của góc giữa hai vectơ u  5;12;13 và n  1;2;2 bằng 7 . 39 2
d) Góc giữa đường thẳng  và mặt phẳng P (làm tròn đến hàng đơn vị của độ) bằng 83 .
B. VIẾT TRÊN TỜ GIẤY THI
Phần III (1 điểm). Thí sinh trả lời từ câu 1 đến câu 4. Đối với mỗi câu, thí sinh chỉ viết kết quả, không trình bày suy luận.
Câu 1. Giả sử doanh số của một sản phẩm mới tuân theo quy luật logistic được mô hình hóa bằng hàm số f t 5000 
,t  0 , trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi 1 5et
đó, đạo hàm f t sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Câu 2. Một hộp đựng 8 thẻ được đánh số từ 2 đến 9. Bạn Lê lấy ngẫu nhiên một thẻ, ghi lại số trên thẻ rồi
bỏ thẻ vào hộp. Lần thứ hai, bạn Lê cũng lấy ngẫu nhiên một thẻ, ghi lại số trên thẻ rồi bỏ thẻ vào hộp.
Tiếp tục như vậy, sau năm lần bạn Lê đã ghi lại được 5 số. Tính xác suất để trong 5 số ghi được có đúng 2 số chia hết cho 4.
Câu 3. Tại một nút giao thông có hai con đường khác mức. Trên thiết kế, trong không gian Oxyz hai con
đường đó thuộc hai đường thẳng x  2 y  2 : z   d   ; x 2 y 1 : z d  
. Người ta muốn tạo một 1 1 1 1 2 1 2 3
con đường  cắt d ,d lần lượt tại A và B sao cho AB nhỏ nhất. Tính độ dài AB . 1 2
Câu 4. Trong một kì thi tốt nghiệp trung học phổ thông, một tỉnh X có 80% học sinh lựa chọn tổ hợp A00
(gồm các môn Toán, Vật lí, Hoá học). Biết rằng, nếu một học sinh chọn tổ hợp A00 thì xác suất để học
sinh đó đỗ đại học là 0,6; còn nếu một học sinh không chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại
học là 0,7. Chọn ngẫu nhiên một học sinh của tỉnh X đã tốt nghiệp trung học phổ thông trong kì thi trên.
Biết rằng học sinh này đã đỗ đại học, tính xác suất để học sinh đó chọn tổ hợp A00.
Phần IV (3 điểm). Thí sinh trả lời từ câu 5 đến câu 7. Đối với mỗi câu, thí sinh viết quá trình và kết quả suy luận.
Câu 5. Giải phương trình: 2 2 2 x 3x2 2x 6x5 3x 3x7 4  4  4 1 .
Câu 6. Cho hình lăng trụ đứng ABC.A B  C
  có đáy là tam giác vuông tại A , AB  a, AC  a 3 . Gọi M
là trung điểm của CC . Biết góc giữa mặt phẳng  A B  M
  và mặt phẳng đáy bằng 30 . Tính khoảng
cách giữa hai đường thẳng AB và B M  .
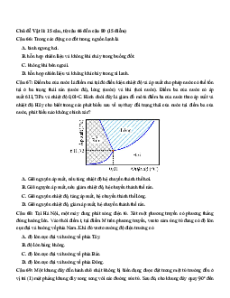
Câu 7. Một cái bình cổ có hình dạng như Hình a. Giả sử mô hình toán mô phỏng việc tạo thành cái bình
cổ đó bằng cách xoay phần diện tích (gạch sọc) được giới hạn bởi đường cong f x 2
 x  8x 12 và
g x  x  6 quanh trục Ox như Hình b. Hãy tính thể tích của cái bình cổ đó.
----------Hết----------