Các dạng toán ôn thi vào lớp 10 có lời giải

CÁC BÀI TOÁN HÌNH ÔN THI VÀO 10
Dạng 1: Chứng minh các điểm thuộc đường tròn Phương pháp
Cách 1: Chứng minh các điểm đó cùng cách đều một điểm O cố định. Khi đó các
điểm đã cho cùng thuộc đường tròn tâm O
Cách 2: Sử dụng tứ giác nội tiếp. Chẳng hạn để chứng minh 5 điểm A, B, C, D, E
cùng thuộc một đường tròn ta chứng minh ABCD, ABCE là tứ giác nội tiếp
Ví dụ 1: Cho hình thoi ABCD có góc A bằng 0
60 , AB = a. Gọi E, F, G, H lần lượt
là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng 6 điểm E, F, G, H,
B, D cùng nằm trên một đường tròn. Xác định tâm và tính bán kính của đường tròn đó theo a. Giải
Gọi O là giao điểm của AC và BD ta có OB = OD
Do ABCD là hình thoi nên ta có AC  BD . Ta có 0 BAD  60 nên 0
BAO  30 (tính chất đường chéo hình thoi)
Tam giác ABO vuông tại O có 0 a
OB  ABsinBAO  OB  a.sin30  2 Xét tam giác vuông ABO có 0
ABO  BAO  90 ( hai góc phụ nhau) mà 0 BAO  30 suy ra 0 ABO  60 hay 0 EBO  60 1
OE  AB  EB  EA ( tính chất đường trung tuyến trong tam giác vuông và E là 2 trung điểm của AB.
Tam giác EOB là tam giác cân tại E có 0
EBO  60 nên tam giác EBO là tam giác đều  OE  OB (1)
Chứng minh tương tự với các tam giác vuông BOC ta có OB = OF (2)
Chứng minh tương tự với các tam giác vuông COD ta có OD = OG (3)
Chứng minh tương tự với các tam giác vuông DOA ta có OD = OH (4)
Mà OD = OB ( vì O là tâm của hình thoi ABCD) nên kết hợp với (1), (2), (3),(4) ta
có: OE = OB = OF = OC = OG = OD = OH
Vậy 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn tâm O. Bán kính a OB  2
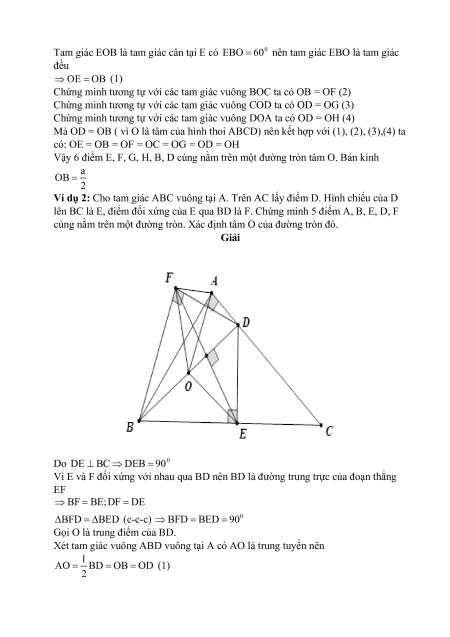
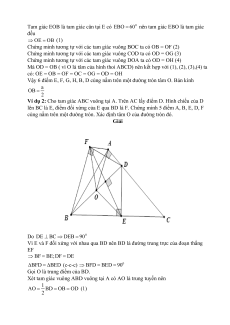
Ví dụ 2: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D
lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F
cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó. Giải Do 0 DE  BC  DEB  90
Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF  BF  BE;DF  DE BFD  BED (c-c-c) 0  BFD  BED  90
Gọi O là trung điểm của BD.
Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên 1 AO  BD  OB  OD (1) 2
Tam giác vuông BDE vuông tại E có OE là trung tuyến nên 1 EO  BD  OB  OD (2) 2
Tam giác vuông BFDvuông tại F có OF là trung tuyến nên 1 FO  BD  OB  OD 2 (3)
Từ (1), (2), (3) OA  OB  OD  OE  OF . Vậy 5 điểm A, B, E, D, F cùng nằm
trên một đường tròn tâm O với O là trung điểm của BC.
Dạng 2:Tứ giác nội tiếp Phương pháp
Để chứng minh tứ giác nội tiếp ta có thể sử dụng một trong các phương pháp sau Phương pháp 1:
Tứ giác có tổng hai góc đối bằng 1800. Phương pháp 2:
Tứ giác có 4 đỉnh cách đều một điểm (mà ta có thể xác định được).
Điểm đó là tâm của đường tròn ngoại tiếp tứ giác. Phương pháp 3:
Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc  Phương pháp 4:
Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.
(tương tự phương pháp 1) Phương pháp 5:
Thuận: Nếu một tứ giác nội tiếp trong một đường tròn thì tích của hai
đường chéo bằng tổng các tích của các cặp cạnh đối diện Định lý
Đảo: Nếu một tứ giác thỏa mãn điều kiện tổng các tích của các cặp
Ptoleme hay đẳng cạnh đối diện bằng tích của hai đường chéo thì tứ giác đó nội tiếp một thức Ptoleme đường tròn.
Ví dụ 1: Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp. Giải
Gọi O là trung điểm của BC. Xét BB’C có : 0 BB'C  90 (giả thiết)
OB’ là đường trung tuyến ứng với cạnh huyền  OB’ = OB = OC = r (1) Xét BC’C có : 0 BC'C  90 (giả thiết)
Tương tự trên  OC’ = OB = OC = r (2)
Từ (1) và (2)  B, C’, B’, C  (O; r)  Tứ giác BC’B’C nội tiếp đường tròn.
Ví dụ 2: Cho nửa đường tròn tâm O đường kính AB, kẻ tiếp tuyến Bx và lấy hai
điểm C và D thuộc nửa đường tròn. Các tia AC và AD cắt Bx lần lượt ở E, F( F ở giữa B và E) 1. Chứng minh: ABD  DFB.
2. Chứng minh rằng CEFD là tứ giác nội tiếp. Giải