ƠNG
I MỆNH ĐỀ TOÁN HỌC TẬP HỢP CHƯ
BÀI 1: MỆNH ĐỀ TOÁN HỌC LÝ THUYẾT. I =
I. MỆNH ĐỀ TOÁN HỌC
Mỗi mệnh đề phải hoặc đúng hoặc sai.
Mỗi mệnh đề không thể vừa đúng, vừa sai.
II. MỆNH ĐỀ CHỨA BIẾN
Xét câu “ n chia hết cho 3 ” (với n là số tự nhiên).
Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề.
Tuy nhiên, nếu thay n bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn:
• Với n = 21 ta được mệnh đề “21 chia hết cho 3”. Đây là mệnh đề đúng.
• Với n =10 ta được mệnh đề “10 chia hết cho 3”. Đây là mệnh đề sai.
Ta nói rằng câu “ n chia hết cho 3 ” là một mệnh đề chứa biến.
III. PHỦ ĐỊNH CỦA MỘT MỆNH ĐỀ
Cho mệnh đề P . Mệnh đề “Không phải P ” được gọi là mệnh phủ định của mệnh đề P
và kí hiệu là P . Khi đó, ta có
• P đúng khi P sai.
• P sai khi P đúng.
IV. MỆNH ĐỀ KÉO THEO
Mệnh đề '' Nếu P thì Q '' được gọi là mệnh đề kéo theo, và kí hiệu là P . Q
Mệnh đề P Q còn được phát biểu là '' P kéo theo Q '' hoặc '' Từ P suy ra Q '' .
Mệnh đề P Q chỉ sai khi P đúng và Q sai.
Như vậy, ta chỉ xét tính đúng sai của mệnh đề P Q khi P đúng. Khi đó, nếu Q đúng
thì P Q đúng, nếu Q sai thì P Q sai.
Các định lí, toán học là những mệnh đề đúng và thường có dạng P . Q
Khi đó ta nói P là giả thiết, Q là kết luận của định lí, hoặc P là điều kiện đủ để có Q
hoặc Q là điều kiện cần để có . P
V. MỆNH ĐỀ ĐẢO – HAI MỆNH ĐỀ TƯƠNG ĐƯƠNG
Mệnh đề Q P được gọi là mệnh đề đảo của mệnh đề P . Q
Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
Nếu cả hai mệnh đề P Q và Q P đều đúng ta nói P và Q là hai mệnh đề tương đương.
Khi đó ta có kí hiệu P Q và đọc là P tương đương Q, hoặc P là điều kiện cần và đủ
để có Q, hoặc P khi và chỉ khi . Q
VI. KÍ HIỆU VÀ
Ví dụ: Câu '' Bình phương của mọi số thực đều lớn hơn hoặc bằng 0 ' là một mệnh đề.
Có thể viết mệnh đề này như sau 2 x : x 0 hay 2 x 0, x .
Kí hiệu đọc là '' với mọi '' .
Ví dụ: Câu '' Có một số nguyên nhỏ hơn 0 '' là một mệnh đề.
Có thể viết mệnh đề này như sau n : n 0.
Kí hiệu đọc là '' có một '' (tồn tại một) hay '' có ít nhất một '' (tồn tại ít nhất một).
Mệnh đề phủ định của mệnh đề " x
X , P(x)" là " x
X , P(x)".
Ví dụ: Cho mệnh đề 2 “ x
, x − x + 7 0” . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải
Phủ định của mệnh đề 2 “ x
, x − x + 7 0” là mệnh đề 2 “ x
, x − x + 7 0” .
Mệnh đề phủ định của mệnh đề " x
X , P(x)" là " x
X , P(x)".
Ví dụ: Cho mệnh đề 2 “ x
, x − x − 6 = 0” . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải
Phủ định của mệnh đề 2 “ x
, x − x − 6 = 0” là mệnh đề 2 “ x
, x − x − 6 0” . Câu 1:
Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
a) Tích hai số thực trái dấu là một số thực âm.
b) Mọi số tự nhiên đều là dương.
c) Có sự sống ngoài Trái Đất
d) Ngày 1 tháng 5 là ngày Quốc tế Lao động. Câu 2:
Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.
a) A: “ 5 là một phân số". 1, 2 b) B: "Phương trình 2
x + 3x + 2 = 0 có nghiệm". c) 2 3 2+3 C :"2 + 2 = 2 " .
d) D: “Số 2025 chia hết cho 15". Câu 3:
Cho n là số tự nhiên. Xét các mệnh đề:
P: “n là một số tự nhiên chia hết cho 16".
Q: "n là một số tự nhiên chia hết cho 8".
a) Phát biểu mệnh đề P Q . Nhận xét tính đúng sai của mệnh đề đó.
b) Phát biểu mệnh đề đảo của mệnh đề P Q . Nhận xét tính đúng sai của mệnh đề đó. Câu 4:
Cho tam giác ABC. Xét các mệnh đề: P: “Tam giác ABC cân”.
Q: "Tam giác ABC có hai đường cao bằng nhau".
Phát biểu mệnh đề P Q bằng bốn cách. Câu 5:
Dùng kí hiệu " hoặc " để viết các mệnh đề sau:
a) Có một số nguyên không chia hết cho chính nó.
b) Mọi số thực cộng với 0 đều bằng chính nó. Câu 6:
Phát biểu các mệnh đề sau: a) 2 x , x 0 1 b) x , x . x Câu 7:
Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó: a) 2 x
, x 2x − 2 b) 2 x
, x 2x −1 1 c) x , x + 2 x d) 2 x
, x − x +1 0
II HỆ THỐNG BÀI TẬP. = BÀI TẬP. 1 =
Câu 1. Trong các câu sau, câu nào là mệnh đề?
a) Trung Quốc là nước đông dân nhất thế giới;
b) Bạn học trường nào?
c) Không được làm việc riêng trong trường học;
d) Tôi sẽ sút bóng trúng xà ngang.
Câu 1. 2. Xét tính đúng sai của các mệnh đề sau: 10 a) ; 3
b) Phương trình 3x + 7 = 0 có nghiệm;
c) Có ít nhất một số cộng với chính nó bằng 0; d) 2022 là hợp số.
Câu 1. 3. Cho hai câu sau:
P: “Tam giác ABC là tam giác vuông”;
Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”.
Hãy phát biểu mệnh đề tương đương P Q xét tính đúng sai của mệnh đề này.
Câu 1. 4. Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai chúng.
P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;
Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”.
Câu 1. 5. Với hai số thực a và b, xét các mệnh đề 2 2
P :"a b "và Q :"0 a b" .
a) Hãy phát biểu mệnh đề P Q .
b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a.
c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b.
Câu 1. 6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó. Q: “ n
, n chia hết cho n+1”.
Câu 1. 7. Dùng kí hiệu ,
để viết các mệnh đề sau:
P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”;
Q: “ Có một số thực cộng với chính nó bằng 0”.
BÀI TẬP TỰ LUẬN. 2 =
DẠNG 1: XÁC ĐỊNH MỀNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN PHƯƠNG PHÁP
Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:
Mệnh đề là một câu khẳng định đúng hoặc sai.
Một mệnh đề không thể vừa đúng hoặc vừa sai
Chuyên đề dạy thêm Toán 10 Học kì 1 Cánh diều
268
134 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Chuyên đề dạy thêm Toán 10 Cánh diều nhằm giúp Giáo viên có thêm tài liệu tham khảo tài liệu môn Toán 10 Cánh diều.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(268 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 15 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án150.000 ₫ 7.9 K 3.9 K lượt tải
-
5 đề thi Toán 10 Cuối kì 1 Kết nối tri thức cấu trúc mới90.000 ₫ 269 135 lượt tải
-
Bộ 15 đề thi cuối kì 1 Toán 10 Cánh diều có đáp án150.000 ₫ 4.2 K 2.1 K lượt tải
-
Giáo án Toán 10 Cánh diều (năm 2024) | Giáo án Toán 10 mới, chuẩn nhất300.000 ₫ 4.5 K 2.2 K lượt tải
-
Đề cương ôn tập Cuối kì 1 Toán 10 Kết nối tri thức80.000 ₫ 172 86 lượt tải
-
5 đề thi Toán 10 Cuối kì 1 Cánh diều cấu trúc mới90.000 ₫ 279 140 lượt tải
-
5 đề thi Toán 10 Cuối kì 1 Chân trời sáng tạo cấu trúc mới90.000 ₫ 168 84 lượt tải
-
Bài giảng Powerpoint Toán 10 Chân trời sáng tạo300.000 ₫ 1.8 K 0.9 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 10
Xem thêm-
Bộ 13 đề thi cuối kì 1 Tiếng Anh 10 Global success có đáp án150.000 ₫ 9.9 K 5 K lượt tải
-
Bộ đề thi cuối kì 1 Vật lí 10 Kết nối tri thức có đáp án50.000 ₫ 4 K 2 K lượt tải
-
Bộ 9 đề thi cuối kì 1 Hóa học 10 Kết nối tri thức có đáp án120.000 ₫ 4 K 2 K lượt tải
-
Bộ đề thi cuối kì 1 Tin học 10 Kết nối tri thức có đáp án80.000 ₫ 3.9 K 2 K lượt tải
-
Bài giảng Powerpoint KTPL 10 Kết nối tri thức200.000 ₫ 2 K 1 K lượt tải
-
Bộ 15 đề thi cuối kì 1 Ngữ Văn 10 Chân trời sáng tạo có đáp án150.000 ₫ 5.9 K 2.9 K lượt tải
-
Bộ 9 đề thi cuối kì 1 Hóa học 10 Chân trời sáng tạo có đáp án150.000 ₫ 2.2 K 1.1 K lượt tải
-
Bộ 15 đề thi cuối kì 1 Ngữ Văn 10 Kết nối tri thức có đáp án150.000 ₫ 5.3 K 2.7 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
BÀI 1: MỆNH ĐỀ TOÁN HỌC
I. MỆNH ĐỀ TOÁN HỌC
Mỗi mệnh đề phải hoặc đúng hoặc sai.
Mỗi mệnh đề không thể vừa đúng, vừa sai.
II. MỆNH ĐỀ CHỨA BIẾN
Xét câu “
n
chia hết cho
3
” (với
n
là số tự nhiên).
Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề.
Tuy nhiên, nếu thay
n
bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn:
• Với
21n =
ta được mệnh đề “21 chia hết cho 3”. Đây là mệnh đề đúng.
• Với
10n =
ta được mệnh đề “10 chia hết cho 3”. Đây là mệnh đề sai.
Ta nói rằng câu “
n
chia hết cho
3
” là một mệnh đề chứa biến.
III. PHỦ ĐỊNH CỦA MỘT MỆNH ĐỀ
Cho mệnh đề
P
. Mệnh đề “Không phải
P
” được gọi là mệnh phủ định của mệnh đề
P
và kí hiệu là
P
. Khi đó, ta có
•
P
đúng khi
P
sai.
•
P
sai khi
P
đúng.
IV. MỆNH ĐỀ KÉO THEO
Mệnh đề
''
Nếu
P
thì
Q
''
được gọi là mệnh đề kéo theo, và kí hiệu là
.PQ
Mệnh đề
PQ
còn được phát biểu là
''
P
kéo theo
Q
''
hoặc
''
Từ
P
suy ra
Q
''
.
Mệnh đề
PQ
chỉ sai khi
P
đúng và
Q
sai.
Như vậy, ta chỉ xét tính đúng sai của mệnh đề
PQ
khi
P
đúng. Khi đó, nếu
Q
đúng
thì
PQ
đúng, nếu
Q
sai thì
PQ
sai.
Các định lí, toán học là những mệnh đề đúng và thường có dạng
.PQ
Khi đó ta nói
P
là giả thiết,
Q
là kết luận của định lí, hoặc
P
là điều kiện đủ để có
Q
CHƯƠNG
I
MỆNH ĐỀ TOÁN HỌC
TẬP HỢP
LÝ THUYẾT.
I
=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
hoặc
Q
là điều kiện cần để có
.P
V. MỆNH ĐỀ ĐẢO – HAI MỆNH ĐỀ TƯƠNG ĐƯƠNG
Mệnh đề
QP
được gọi là mệnh đề đảo của mệnh đề
.PQ
Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng.
Nếu cả hai mệnh đề
PQ
và
QP
đều đúng ta nói
P
và
Q
là hai mệnh đề tương
đương.
Khi đó ta có kí hiệu
PQ
và đọc là
P
tương đương
,Q
hoặc
P
là điều kiện cần và đủ
để có
,Q
hoặc
P
khi và chỉ khi
.Q
VI. KÍ HIỆU
VÀ
Ví dụ: Câu
''
Bình phương của mọi số thực đều lớn hơn hoặc bằng
0''
là một mệnh đề.
Có thể viết mệnh đề này như sau
2
:0xx
hay
2
0, .xx
Kí hiệu
đọc là
''
với mọi
''
.
Ví dụ: Câu
''
Có một số nguyên nhỏ hơn 0
''
là một mệnh đề.
Có thể viết mệnh đề này như sau
: 0.nn
Kí hiệu
đọc là
''
có một
''
(tồn tại một) hay
''
có ít nhất một
''
(tồn tại ít nhất một).
Mệnh đề phủ định của mệnh đề
" , ( )"x X P x
là
" , ( )".x X P x
Ví dụ: Cho mệnh đề
2
“ , 7 0”x x x − +
. Tìm mệnh đề phủ định của mệnh đề trên?
Lời giải
Phủ định của mệnh đề
2
“ , 7 0”x x x − +
là mệnh đề
2
“ , 7 0”x x x − +
.
Mệnh đề phủ định của mệnh đề
" , ( )"x X P x
là
" , ( )".x X P x
Ví dụ: Cho mệnh đề
2
“ , 6 0”x x x − − =
. Tìm mệnh đề phủ định của mệnh đề trên?
Lời giải
Phủ định của mệnh đề
2
“ , 6 0”x x x − − =
là mệnh đề
2
“ , 6 0”x x x − −
.
Câu 1: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?
a) Tích hai số thực trái dấu là một số thực âm.
b) Mọi số tự nhiên đều là dương.
c) Có sự sống ngoài Trái Đất
d) Ngày 1 tháng 5 là ngày Quốc tế Lao động.
Câu 2: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ
định đó.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a) A: “
5
1,2
là một phân số".
b) B: "Phương trình
2
3 2 0xx+ + =
có nghiệm".
c)
2 3 2 3
:"2 2 2 "C
+
+=
.
d) D: “Số 2025 chia hết cho 15".
Câu 3: Cho n là số tự nhiên. Xét các mệnh đề:
P: “n là một số tự nhiên chia hết cho 16".
Q: "n là một số tự nhiên chia hết cho 8".
a) Phát biểu mệnh đề
PQ
. Nhận xét tính đúng sai của mệnh đề đó.
b) Phát biểu mệnh đề đảo của mệnh đề
PQ
. Nhận xét tính đúng sai của mệnh đề đó.
Câu 4: Cho tam giác ABC. Xét các mệnh đề:
P: “Tam giác ABC cân”.
Q: "Tam giác
ABC
có hai đường cao bằng nhau".
Phát biểu mệnh đề
PQ
bằng bốn cách.
Câu 5: Dùng kí hiệu
"
hoặc
" để viết các mệnh đề sau:
a) Có một số nguyên không chia hết cho chính nó.
b) Mọi số thực cộng với 0 đều bằng chính nó.
Câu 6: Phát biểu các mệnh đề sau:
a)
2
,0xx
b)
1
,xx
x
.
Câu 7: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định
đó:
a)
2
, 2 2x x x −
b)
2
, 2 1x x x −
c)
1
,2xx
x
+
d)
2
, 1 0x x x − +
Câu 1. Trong các câu sau, câu nào là mệnh đề?
HỆ THỐNG BÀI TẬP.
II
=
BÀI TẬP.
1
=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a) Trung Quốc là nước đông dân nhất thế giới;
b) Bạn học trường nào?
c) Không được làm việc riêng trong trường học;
d) Tôi sẽ sút bóng trúng xà ngang.
Câu 1. 2. Xét tính đúng sai của các mệnh đề sau:
a)
10
3
;
b) Phương trình
3 7 0x +=
có nghiệm;
c) Có ít nhất một số cộng với chính nó bằng 0;
d) 2022 là hợp số.
Câu 1. 3. Cho hai câu sau:
P: “Tam giác ABC là tam giác vuông”;
Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”.
Hãy phát biểu mệnh đề tương đương
PQ
xét tính đúng sai của mệnh đề này.
Câu 1. 4. Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai chúng.
P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”;
Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”.
Câu 1. 5. Với hai số thực a và b, xét các mệnh đề
22
:" "P a b
và
:"0 "Q a b
.
a) Hãy phát biểu mệnh đề
PQ
.
b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a.
c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b.
Câu 1. 6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.
Q: “
n
, n chia hết cho n+1”.
Câu 1. 7. Dùng kí hiệu
,
để viết các mệnh đề sau:
P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”;
Q: “ Có một số thực cộng với chính nó bằng 0”.
DẠNG 1: XÁC ĐỊNH MỀNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN
PHƯƠNG PHÁP
Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:
Mệnh đề là một câu khẳng định đúng hoặc sai.
Một mệnh đề không thể vừa đúng hoặc vừa sai
BÀI TẬP TỰ LUẬN.
2
=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập
X
nào
đó mà với mỗi giá trị chứa biến thuộc
X
ta được một mệnh đề.
Bài 1. Các câu sau đây, có bao nhiêu câu là mệnh đề?
(1) Ở đây đẹp quá!
(2) Phương trình
2
3 1 0xx− + =
vô nghiệm
(3) 16 không là số nguyên tố
(4) Hai phương trình
2
4 3 0xx− + =
và
2
3 1 0xx− + + =
có nghiệm chung.
(5) Số
có lớn hơn
3
hay không?
(6) Italia vô địch Worldcup 2006
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
Bài 2. Cho ba mệnh đề sau, với
n
là số tự nhiên
(1)
8n +
là số chính phương
(2) Chữ số tận cùng của
n
là 4
(3)
1n −
là số chính phương
Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng
mệnh đề nào sai?
Bài 3. Trong các câu sau, có bao nhiêu câu là mệnh đề, mệnh đề chứa biến, không là mệnh đề?
- Hãy cố gắng học thật tốt!
- Số
( )
;3B = −
chia hết cho
)
1;3AB = −
.
- Số
)
1;A= +
là số nguyên tố.
- Số
2
| 1 0B x x= + =
là số chẵn.
Bài 4. Tại Tiger Cup 98 có bốn đội lọt vào vòng bán kết: Việt Nam, Singapor, Thái Lan và
Inđônêxia. Trước khi thi đấu vòng bán kết, ba bạn Dung, Quang, Trung dự đoán như sau:
Dung: Singapor nhì, còn Thái Lan ba.
Quang: Việt Nam nhì, còn Thái Lan tư.
Trung: Singapor nhất và Inđônêxia nhì.
Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy?
Bài 5: Trong các phát biểu sau, phát biểu nào không phải là mệnh đề, giải thích?
1/ Hải Phòng là một thành phố của Việt Nam.
2/ Bạn có đi xem phim không?
3/
10
21−
chia hết cho
11
.
4/
2763
là hợp số.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
5/
2
3 2 0xx− + =
.
Bài 6: Trong các phát biểu sau, phát biểu nào là mệnh đề, xét tính đúng, sai của mệnh đề đó.
(I): “17 là số nguyên tố”
(II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”
(III): “Các em C14 hãy cố gắng học tập thật tốt nhé !”
(IV): “Mọi hình thoi đều nội tiếp được đường tròn”
Bài 7: Cho các câu sau đây:
(I): “Phan-xi-păng là ngọn núi cao nhất Việt Nam”.
(II): “
2
9,86
”.
(III): “Mệt quá!”.
(IV): “Chị ơi, mấy giờ rồi?”.
Hỏi có bao nhiêu câu là mệnh đề?
Bài 8: Trong các câu sau, có bao nhiêu câu là mệnh đề đúng
(I): Hãy cố gắng học thật tốt!
(II): Số
20
chia hết cho
6
.
(III): Số
5
là số nguyên tố.
(IV): Với mọi
k
,
2k
là số chẵn.
Bài 9: Trong các câu dưới đây, câu nào là mệnh đề, câu nào là mệnh đề chứa biến:
a)
2 5 0−
.
b) 4 + x = 3.
c) Hãy trả lời câu hỏi này!.
d) Paris là thủ đô nước Ý.
Bài 10. Trong các mệnh đề sau, xét tính đúng sai của các mệnh đề sau?
a. Điều kiện cần và đủ để
xy
là
33
xy
.
b. Điều kiện cần và đủ để số tự nhiên
n
chia hết cho 2 và 3 là số tự nhiên đó chia hết cho
12.
c. Điều kiện cần và đủ để
22
0ab+=
là cả hai số
a
và
b
đều bằng 0.
d. Điều kiện cần và đủ để số tự nhiên
n
chia hết cho 3 là
2
n
chia hết cho 3.
Bài 11. Tìm tất cả các giá trị thực của
x
để mệnh đề
”:“ 2 1 1Px−
là mệnh đề đúng?
Bài 12. Tìm tất cả các giá trị thực của
x
để mệnh đề
”: “2 1 0Px−
là mệnh đề sai?
Bài 13. Tìm tất cả các giá trị thực của
x
để mệnh đề
2
”:“ 5 4 0P x x+ + =
là mệnh đề sai?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 14. Xét câu:
( )
:Pn
“
n
là số thự nhiên nhỏ hơn 50 và
n
chia hết cho 12”. Với giá trị nào của
n
sau đây thì
( )
Pn
là mệnh đề đúng. Khi đó số các giá trị của
n
bằng bao nhiêu?
DẠNG 2: XÉT TÍNH ĐÚNG SAI CỦA MỘT MỆNH ĐỀ
PHƯƠNG PHÁP
Để xét tính đúng, sai của một mệnh đề ta cần nhớ nội dung sau:
Một câu khẳng định đúng là mệnh đề đúng.
Một câu khẳng định sai là mệnh đề sai.
Không có mệnh đề vừa đúng vừa sai.
Bài 1. Xét tính đúng, sai của mệnh đề sau:
M: “π là một số hữu tỉ”.
N: “Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ ba”.
Bài 2. Xét tính đúng, sai của mệnh đề sau:
A: “Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn”.
B: “Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn”.
C: “Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”.
D: “Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”.
Bài 3. Xét tính đúng, sai của mệnh đề sau:
P: “
2
2 4.
− −
”.
Q: “
2
4 16.
”.
Bài 4. Xét tính đúng, sai của mệnh đề sau:
X: “
23 5 2 23 10
”.
Y: “
23 5 2 23 10. − −
”.
Bài 5. Xét tính đúng, sai của mệnh đề sau:
M: “Số nguyên tố lớn hơn 2 là số lẻ”.
N: “Số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5”.
P: “Bình phương tất cả các số nguyên đều chia hết cho 2”.
Bài 6. Nêu mệnh đề phủ định của mỗi mệnh đề sau và xác định xem mệnh đề phủ định đó đúng hay
sai:
a)
P
: “Phương trình
2
10xx+ + =
có nghiệm”.
b)
Q
: “Năm
2020
là năm nhuận”.
c)
R
: “
327
chia hết cho
3
”.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 7. Cho tam giác
ABC
với đường trung tuyến
AM
. Xét hai mệnh đề
P
: “Tam giác
ABC
vuông tại
A
”;
Q
: “Trung tuyến
AM
bằng nửa cạnh
BC
”
a) Phát biểu mệnh đề
PQ
và cho biết mệnh đề này đúng hay sai.
b) Phát biểu mệnh đề
PQ
và cho biết mệnh đề này đúng hay sai.
Bài 8. Cho hai mệnh đề
P
: “
42
chia hết cho
5
”;
Q
: “
42
chia hết cho
10
”
Phát biểu mệnh đề
PQ
và cho biết mệnh đề này đúng hay sai, tại sao?
Bài 9. Xét hai mệnh đề
P
: “
7
là số nguyên tố”;
Q
: “
6! 1+
chia hết cho
7
”
Phát biểu mệnh đề
PQ
bằng hai cách. Cho biết mệnh đề đó đúng hay sai.
Bài 10. Lập mệnh đề phủ định của mệnh đề: “
n
,
2
1nn++
là số nguyên tố”.
Mệnh đề phủ định đó đúng hay sai?
Bài 11. Xét tinh đúng sai của mệnh đề
2
" , 6 6"x x x
.
Bài 12. Xét tinh đúng sai của mệnh đề “Với mọi giá trị
n
thuộc tập hợp số nguyên,
2
1n +
không chia
hết cho 3”.
Bài 13. Xét tinh đúng sai của mệnh đề “Tồn tại
n
thuộc tập hợp số nguyên,
2
1n +
chia hết cho 4”.
Bài 14. Xét tinh đúng sai của mệnh đề “Nếu
21
a
−
là số nguyên tố thì
a
là số nguyên tố”.
Bài 15. Xét tinh đúng sai của mệnh đề “Nếu
n
và
2
5n
thì
5n
”.
Bài 16. Xét tính đúng sai của mệnh đề: “
32
, 3 4 1n n n n + − +
chia hết cho 6”.
Bài 17. Xác định tính đúng, sai của mệnh đề A : "
2
,0xx
" và tìm mệnh đề phủ định của nó.
Bài 18. Viết mệnh đề phủ định của mệnh đề
2
: , 4 4 1 0A x x x
− + −
và xét tính đúng, sai của
mệnh đề đó.
Bài 19. Xét mệnh đề chứa biến:
( )
32
:" 3 2 0"P x x x x− + =
. Có bao nhiêu giá trị của biến
x
để mệnh
đề trên là mệnh đề đúng ?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
DẠNG 3: PHỦ ĐỊNH MỘT MỆNH ĐỀ
PHƯƠNG PHÁP
Để phủ định một mệnh đề ta thêm hoặc bớt từ “không” hoặc “không phải” trước vị ngữ
của mệnh đề đó.
Ta có thể dùng từ thay thế hoặc đặt lại câu có cùng ý nghĩa.
Mệnh đề phủ định của mệnh đề
' )' ,(x X P x
là
, ( ) .'' x X P x
Mệnh đề phủ định của mệnh đề
' )' ,(x X P x
là
, ( ) .'' x X P x
Để phủ định mệnh đề kéo theo
PQ
ta hiểu
PQ
là “
, ( )x X P x
ta có
( )
Qx
”
nên mệnh đề phủ định là “
, ( )x X P x
ta có
( )
Qx
” .
Phủ định mệnh đề "
P
" là mệnh đề " không phải
P
", kí hiệu
P
.
Tính chất
X
thành không
X
và ngược lại.
Quan hệ
=
thành quan hệ
và ngược lại.
Quan hệ
thành quan hệ
và ngược lại.
Quan hệ
thành quan hệ
và ngược lại.
( )
,x X P x
thành
( )
,x X P x
.
( )
,x X P x
thành
( )
,x X P x
.
( )
, , ,x X y Y P x y
thành
( )
, , ,x X y Y P x y
.
( )
, , ,x X y Y P x y
thành
( )
, , ,x X y Y P x y
.
Nếu
P
đúng thì
P
sai, nếu
P
sai thì
P
đúng.
Bài 1. Nêu mệnh đề phủ định của các mệnh đề sau.
:P
" Trong tam giác tổng ba góc bằng 180
0
"
:Q
" 6 không phải là số nguyên tố"
Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau .
a) Mọi hình vuông đều là hình thoi. b) Có một tam giác cân không phải là tam giác đều.
Bài 3. Lập mệnh đề phủ định của mỗi mệnh đề sau .
a)
2
:0xx
b)
2
:n n n
.
Bài 4. Lập mệnh đề phủ định của mỗi mệnh đề sau
a)
2
: 2 5 0x x x + + =
b)
2
:3 2x x x +
.
Bài 5. Lập mệnh đề phủ định của mỗi mệnh đề sau .
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
:P
“Phương trình
2
10x +=
có nghiệm”
:Q
“
,2 1n N n +
là số lẻ”
Bài 6. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “
( )
*2
,1n n n −
là bội số của
3
”.
Bài 7. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “
2
: 6 5 0x x x − + =
”.
Bài 8. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “
, : 3x y y x = +
”.
Bài 9. Phát biểu mệnh đề phủ định của mệnh đề “
n
chia hết cho
2
và cho
3
thì nó chia hết cho
6
”.
Bài 10. Phát biểu mệnh đề phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng
bằng nhau”.
Bài 11. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó
a)
:nn
chia hết cho
n
. b)
2
:2x Q x =
.
c)
:1x x x +
. d)
2
:3 1x R x x = +
.
Bài 12. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề:
( )( )
, 1 2n n n n + +
là số không chia hết cho
6
.
Bài 13. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định
a)
, , 1a R b R a b +
.
b)
( )
2
22
, , 2a R b R a b a ab b + = + +
.
c)
2
,,a R b R a b
d)
,,abc
mà
0abc+ +
thì
2 2 2
2
abc
ab bc ca
++
− + +
.
Bài 14. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định
P
: “
( )( )( )
: 1 2 3 1n A n n n n = + + + +
không là số chính phương".
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
DẠNG 4: MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO, MỆNH ĐỀ TƯƠNG ĐƯƠNG
PHƯƠNG PHÁP
1. Mệnh đề kéo theo
a. ĐN: Cho hai mệnh đề P và Q. Mệnh đề dạng: “Nếu P thì Q” được gọi là mệnh đề kéo
theo.
- Ký hiệu là: P ⟹ Q.
- Cách xét tính đúng sai của mệnh đề kéo theo P ⟹ Q: Mệnh đề kéo theo P ⟹ Q chỉ sai
khi P đúng và Q sai.
b. Xét tính đúng, sai của mệnh đề kéo theo:
- P ⟹ Q chỉ sai khi P đúng và Q sai.
- Phương pháp xét tính đúng sai của mệnh đề P ⟹ Q
- Quan sát xem P, Q đúng hay sai
- Khi đó P ⟹ Q rơi vào mẫu nào trong 4 mẫu sau
1. Đ ⟹ S→Sai 2. Đ ⟹ Đ 3. 𝐒 ⟹ Đ 4. 𝐒 ⟹ 𝐒 →Đúng
Đặc biệt: Có hai trường hợp mà chỉ cần nhìn vào một trong hai mệnh đề P hoặc Q ta sẽ
biết (P ⟹ Q) luôn đúng: TH1: P sai. TH2: Q đúng.
- Chú ý: P ⟹ Q
chính là P ∩ Q
.
2. Mệnh đề tương đương
a. Mệnh đề đảo: Mệnh đề Q⟹P được gọi là mệnh đề đảo của mệnh đề P⟹Q
b. Mệnh đề tương đương - Điều kiện cần và đủ:
- Nếu cả hai mệnh đề "P ⟹ Q" và "Q ⟹ P" đều đúng ta nói P và Q là hai mệnh đề
tương đương và kí hiệu "P ⟺ Q".
- Lúc đó ta nói: P là điều kiện cần và đủ để có Q hay Q là điều kiện cần và đủ để có P.
Hoặc P nếu và chỉ nếu Q
Hay P khi và chỉ khi Q
Hay Điều kiện cần và đủ để có P là Q.
- Cách xét tính đúng, sai của mệnh đề tương đương :
Mệnh đề P ⇔ Q chỉ đúng khi cả hai mệnh đề kéo theo P ⟹ Q và Q ⟹ P đều đúng. Nói
cách khác mệnh đề P ⇔ Q đúng nếu cả hai mệnh đề P và Q cùng đúng hoặc cùng sai.
Bài 1. Lập mệnh đề
PQ
và xét tính đúng sau của nó, với
:" 4"P
và
2
:" 10"Q
.
Bài 2. Phát biểu mệnh đề đảo của mệnh đề “Nếu
0
A 90=
thì
ABC
là tam giác vuông” và xét tính
đúng sai của nó.
Bài 3. Cho mệnh đề
:"2 3",Q:" 4 6"P − −
. Lập mệnh đề
PQ
và xét tính đúng sai của nó.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 4. Giả sử ABC là một tam giác đã cho. Lập mệnh đề
PQ
và mệnh đề đảo của nó, rồi xét tính
đúng sai của chúng với P:
"
Góc A bằng
90
"
, Q:
2 2 2
""BC AB AC=+
.
Bài 5. Cho
ABC
. Xét mệnh đề
P
: “
ABC
là tam giác cân” và mệnh đề
Q
: “
ABC
có hai đường
trung tuyến bằng nhau”. Lập mệnh đề
PQ
và xét tính đúng sai của nó.
Bài 6. Phát biểu mệnh đề đảo của định lý: “Trong một tam giác cân, các đường cao ứng với các cạnh
bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao?
Bài 7. Cho mệnh đề chứa biến
( )
:5 3P n n+
chia hết cho 3, với
nN
,
( )
:Q n n
chia hết cho 3, với
nN
.
Phát biểu mệnh đề “
( ) ( )
,n N P n Q n
” và từ đó phát biểu mệnh đề đảo. Xét tính đúng
sai của mệnh đề đảo.
Bài 8. Cho hai mệnh đề P và Q:
P:
ABCD
là tứ giác nội tiếp.
Q: Tổng số đo hai góc đối nhau bằng
180
o
.
Hãy phát biểu mệnh đề
PQ
dưới dạng điều kiện cần và đủ.
Bài 9. Cho các mệnh đề :
A: “Nếu
ABC
đều có cạnh bằng a, đường cao là h thì
3
2
a
h =
”;
B: “Tứ giác có bốn cạnh bằng nhau là hình vuông”;
C:”15 là số nguyên tố”;
D:”
125
là một số nguyên”.
Hãy cho biết trong các mệnh đề sau, mệnh đề nào đúng, mệnh đề nào sai:
,,A B B C A D
. Giải thích.
Bài 5. Phát biểu mệnh đề
PQ
và xét tính đúng sai của nó. Giải thích
P: “Bất phương trình
2
3 1 0xx− +
có nghiệm”
Q: “Bất phương trình
2
3 1 0xx− +
vô nghiệm”
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 6. Câu sau đây là biểu đạt của mệnh đề nào?
“Mấy đời bánh đúc có xương
Mấy đời dì ghẻ có thương con chồng.”
“Chuồn chuồn bay thấp thì mưa
Bay cao thì nắng bay vừa thì râm.”
Bài 7. Trên một hòn đảo, tôi đã gặp ba người A, B và C, một người là hiệp sĩ, một người khác là kẻ
bất lương và người kia là gián điệp. Người hiệp sĩ luôn nói sự thật, kẻ bất lương luôn luôn nói
dối và gián điệp có thể nói dối hoặc nói sự thật.
A nói: "Tôi là hiệp sĩ."
B nói, "Tôi là kẻ bất lương."
C nói: "Tôi là gián điệp."
Hỏi ai là gián điệp?
Bài 8. Ba anh em An, Bình, Vinh ngồi làm bài xung quanh một cái bàn được trải khăn mới. Khi phát
hiện có vết mực, bà hỏi thì các cháu lần lượt trả lời:
An: “Em Vinh không làm đổ mực, đấy là do em Bình.”
Bình: “Em Vinh làm đổ mực, anh An không làm đổ mực”.
Vinh: “Theo cháu, Bình không làm đổ mực, còn cháu hôm nay không chuẩn bị bài”.
Biết rằng trong 3 em thì có 2 em nói đúng, 1 em nói sai. Hỏi ai làm đổ mực?
Bài 9. Ếch hay cóc?
Trong một đầm lầy ma thuật, có hai loài lưỡng cư biết nói: cóc luôn luôn nói đúng và ếch luôn
luôn nói sai.
Bốn loài lưỡng cư, Brian, Chris, LeRoy và Mike sống cùng nhau trong đầm lầy này và chúng
đưa ra những tuyên bố sau:
Brian: "Mike và tôi là những loài khác nhau."
Chris: "LeRoy là một con ếch."
LeRoy: "Chris là một con ếch."
Mike: "Trong bốn người chúng tôi, ít nhất hai người là cóc."
Có bao nhiêu loài lưỡng cư là ếch?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 1: Câu nào sau đây không là mệnh đề?
A. Tam giác đều là tam giác có ba cạnh bằng nhau.
B.
31
.
C.
4 5 1−=
.
D. Bạn học giỏi quá!
Câu 2: Câu nào trong các câu sau không phải là mệnh đề?
A.
có phải là một số vô tỷ không?. B.
2 2 5+=
.
C.
2
là một số hữu tỷ. D.
4
2
2
=
.
Câu 3: Trong các câu sau, câu nào là mệnh đề?
A.
12
là số tự nhiên lẻ. B. An học lớp mấy?
C. Các bạn có chăm học không? D. Các bạn hãy làm bài đi!
Câu 4: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi! b) Số 15 là số nguyên tố.
c) Tổng các góc của một tam giác là
180 .
d)
x
là số nguyên dương.
A.
3.
B.
2.
C.
4.
D.
1.
Câu 5: Câu nào sau đây không là mệnh đề?
A. Tam giác đều là tam giác có ba cạnh bằng nhau.
B.
31
.
C.
4 5 1−=
.
D. Bạn học giỏi quá!
Câu 6. Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. “ Nếu I là trung điểm của AB thì IA = IB”.
B. “ Nếu ABCD là hình bình hành thì
AC AB AD=+
’’.
C. “ Nếu x > 2 thì
2x
”
.
D. “ Nếu
,mn
là 2 số nguyên dương và cùng chia hết cho 3 thì
22
mn+
cũng chia hết cho
3”.
Câu 7. Trong các mệnh đề dưới đây, các mệnh đề nào sai.
M: “
2
,4 1 0rr −=
”.
N: “
2
,1nn +
chia hết cho 8”.
X: “
*
,1 2 3 nn + + ++
không chia hết cho 11”.
BÀI TẬP TRẮC NGHIỆM.
2
=
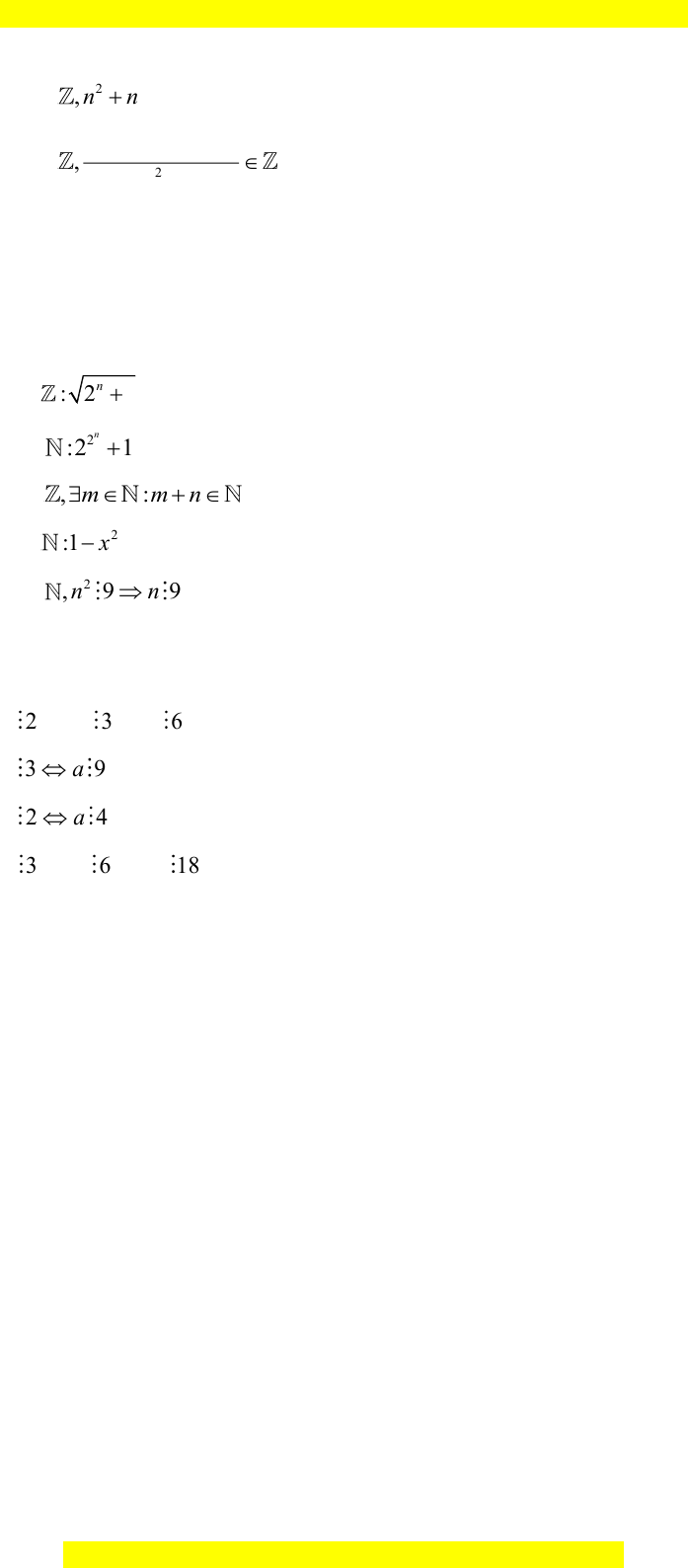
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Q: “
2
,1n n n + +
là một số chẵn”.
E: “
32
2
2 6 3
,
21
x x x
x
x
− + −
+
”.
A. N, X, Q B. M, X, Q C. N, Q, E D. M, Q, E
Câu 8. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
a)
: 2 1
n
n +
là số nguyên.
b)
2
:2 1
n
n +
là số nguyên tố.
c)
,:n m m n +
.
d)
2
:1 0xx −
.
e)
2
, 9 9n n n
.
A. 1. B. 2. C. 3. D. 4.
Câu 9. Cho các mệnh đề sau:
(1)
2a
và
3a
6a
.
(2)
39aa
.
(3)
24aa
.
(4)
3a
và
6a
thì
18a
.
(5)
00a b a+
và
0b
.
(6)
00ab a= =
hoặc
0b =
.
(7) Hai tam giác bằng nhau khi và chỉ khi hai tam giác đó đồng dạng.
(8) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền
bằng một nửa cạnh huyền.
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
A. 4. B. 6. C. 5. D. 7.
Câu 10. Cho ba mệnh đề sau, với
n
là số tự nhiên:
(1)
8n +
là số chính phương
(2) Chữ số tận cùng của
n
là 4
(3)
1n −
là số chính phương
Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng
mệnh đề nào sai?
A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai
B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai.
D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
Câu 11. Mệnh đề nào sau đây đúng?
A.
3.
B.
2
16.
C.
35 6.
D.
36 6.
Câu 12. Mệnh đề nào sau đây sai?
A. 30 chia hết cho 5. B. 30 là bội số của 5.
C. 30 là ước số của 5. D. 5 là ước số của 30.
Câu 13. Mệnh đề nào là sau đây sai?
A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.
B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông
.
C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại
.
D. Một tam giác là đều khi và chỉ khi nó là tam giác cân và có một góc bằng
60 .
Câu 14. Mệnh đề nào dưới đây đúng?
A. Nếu tứ giác
ABCD
có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác
ABCD
là hình bình hành.
B. Nếu tứ giác
ABCD
một cặp cạnh đối song song thì tứ giác
ABCD
là hình bình hành.
C. Nếu tứ giác
ABCD
có một cặp cạnh đối bằng nhau thì tứ giác
ABCD
là hình bình hành.
D. Nếu tứ giác
ABCD
có hai đường chéo vuông góc với nhau thì tứ giác
ABCD
là hình
bình hành.
Câu 15. Mệnh đề nào sau đây sai?
A. 2 là số nguyên tố. B. 1 là số nguyên tố.
C. 5 là số nguyên tố. D. 6 không phải là số nguyên tố.
Câu 16. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A.
2
2 4.
− −
B.
2
4 16.
C.
23 5 2 23 2.5.
D.
23 5 2 23 2.5. − −
Câu 17. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.
B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông
.
C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại
.
D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến bằng nhau và có một
góc bằng
60 .
Câu 18. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. Nếu số nguyên
n
có chữ số tận cùng là
5
thì số nguyên
n
chia hết cho
5.
B. Nếu tứ giác
ABCD
có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác
ABCD
là hình bình hành.
C. Nếu tứ giác
ABCD
là hình chữ nhật thì tứ giác
ABCD
có hai đường chéo bằng nhau.
D. Nếu tứ giác
ABCD
là hình thoi thì tứ giác
ABCD
có hai đường chéo vuông góc với
nhau.
Câu 19. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
A. Nếu số nguyên
n
có tổng các chữ số bằng
9
thì số tự nhiên
n
chia hết cho
3.
B. Nếu
xy
thì
22
.xy
C. Nếu
xy=
thì
. . .t x t y=
D. Nếu
xy
thì
33
.xy
Câu 20. Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A.
"ABC
là tam giác đều
Tam giác
ABC
cân
".
B.
"ABC
là tam giác đều
Tam giác
ABC
cân và có một góc
60 ".
C.
"ABC
là tam giác đều
ABC
là tam giác có ba cạnh bằng nhau
".
D.
"ABC
là tam giác đều
Tam giác
ABC
có hai góc bằng
60 ".
Câu 21. Mệnh đề nào sau đây đúng?
A.
( )
:1n n n +
là số chính phương. B.
( )
:1n n n +
là số lẻ.
C.
( )( )
: 1 2n n n n + +
là số lẻ. D.
( )( )
: 1 2n n n n + +
chia hết cho
6.
Câu 22. Tìm mệnh đề đúng
A.
5
,3nn −
là bội số của 7. B.
2
: 7 15 0x x x − +
.
C.
32
: 2 8 16 0x x x x + + + =
. D.
2
:1nn +
chia hết cho 4.
Câu 23. Trong các mệnh đề sau, mệnh đề nào đúng?
A.
3
,n n n −
không chia hết cho 3. B.
2
, 3 9x x x
.
C.
2
,1k k k + +
là một số chẵn. D.
32
2
2 6 3
,
21
x x x
x
x
− + −
+
.
Câu 24. Trong các mệnh đề sau, mệnh đề nào sai?
A.
2
,x x x
. B.
, 6 6x x x
.
C.
2
,1nn +
không chia hết cho 3. D.
2
,7aa =
.
Câu 25. Trong các mệnh đề sau, mệnh đề nào đúng?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
2
, 5 0xx + =
. B.
42
, 5 4 0x x x + + =
.
C.
3
,n n n −
chia hết cho 3. D.
52
,x x x
.
Câu 26. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Phương trình
32
3 3 0x x x+ − − =
có 2 nghiệm nguyên dương.
B.
2
: 6 10 0x R x x − + −
.
C.
2
1
“ : ”
4
x x x − −
.
D. Bất phương trình
2
1x
x
x
−
có tập nghiệm là
\0R
.
Câu 27. Trong các mệnh đề sau mệnh đề nào sai?
A.
2 3 99 100
4 4 4 .... 4 4+ + + + +
chia hết cho 5.
B.
2
:1nn +
không chia hết cho
4
.
C.
:2 1
n
nN −
chia hết cho
7
.
D.
3 3 3 3
1 2 3 .... 100+ + + +
không chia hết cho
5050
.
Câu 28. Có bao nhiêu số nguyên
n
để mệnh đề “
32
2 7 1n n n+ + +
chia hết cho
21n −
” là đúng ?
A.
3
. B.
2
. C.
4
. D.
5
.
Câu 29: Cho các mệnh đề sau, mệnh đề nào là mệnh đề sai
A.
2
:4 1 0xx − =
. B.
2
:x x x
.
C.
2
:1nn +
không chia hết cho 3. D.
2
:n n n
.
Câu 30: Cho các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng ?
A. Nếu tứ giác ABCD là hình thang cân thì 2 góc đối bù nhau.
B. Nếu
ab=
thì
..a c b c=
.
C. Nếu
ab
thì
22
ab
.
D. Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2.
Câu 31: Dùng kí hiệu
,
để phát biểu mệnh đề "Có một số hữu tỉ mà nghịch đảo của nó lớn hơn
chính nó".
A.
1
:nn
n
B.
1
:nn
n
C.
1
:nn
n
D.
1
:nn
n
.
Câu 32: Hãy chọn mệnh đề đúng:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. Phương trình:
2
9
0
3
x
x
−
=
−
có một nghiệm là . B.
2
: 0.x x x +
C.
2
: 2 0.x x x − +
D.
2
:2 6 2 10 1.x x x + +
Câu 33: Cho mệnh đề
2
1
“ : ”
4
xxA x + −=
. Lập mệnh đề phủ định của mệnh đề
A
và xét
tính đúng sai của nó.
A.
2
1
“ : ”
4
A x x x= + −
. Đây là mệnh đề đúng.
B.
2
1
“ : ”
4
A x x x= + −
. Đây là mệnh đề đúng.
C.
2
1
“ : ”
4
A x x x= + −
. Đây là mệnh đề đúng.
D.
2
1
“ : ”
4
A x x x= + −
. Đây là mệnh đề sai.
Câu 34. Phủ định của mệnh đề: “Hình thoi có hai đường chéo vuông góc với nhau” là:
A.“Hai đường chéo của hình thoi vuông góc với nhau”.
B.“Hình thoi có hai đường chéo không vuông góc với nhau”.
C.“Hình thoi có hai đường chéo bằng nhau”.
D.“Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau”.
Câu 35. Phủ định của mệnh đề: “
2
:1nn +
không chia hết cho 3” là:
A. “
2
:1nn +
chia hết cho 3”. B. “
2
:1nn +
không chia hết cho
3”.
C. “
2
:1nn +
chia hết cho 3”. D. “
2
:1nn+
không chia hết cho
3”.
Câu 36. Phủ định của mệnh đề: “
2
: 1 0xx +
” là:
A.“
2
: 1 0xx +
” B. “
2
: 1 0xx +
” C. “
2
: 1 0xx +
” D.“
2
: 1 0xx + =
”
Câu 37. Phủ định của mệnh đề P: “
2
: 3 2 0x x x − + =
” là:
A.
P
: “
2
: 3 2 0x x x − +
” B.
P
: “
2
: 3 2 0x x x − + =
”
C.
P
: “
2
: 3 2 0x x x − +
” D.
P
: “
2
: 3 2 0x x x − +
”
Câu 38. Phủ định của mệnh đề: “
2
:1x x x + +
là số dương” là:
A. “
2
:1x x x + +
là số không dương” B. “
2
:1x x x + +
là số âm”
C. “
2
:1x x x + +
là số dương” D. “
2
:1x x x + +
là số dương”
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 39. Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”.
A. Mọi động vật đều không di chuyển. B. Mọi động vật đều đứng yên.
C. Có ít nhất một động vật không di chuyển. D. Có ít nhất một động vật di chuyển.
Câu 40. Phủ định của mệnh đề
2
" ,5 3 1"x x x − =
là
A.
2
" ,5 3 "x x x −
. B.
2
" ,5 3 1"x x x − =
.
C.
2
" x ,5x 3 1"x −
. D.
2
" ,5 3 1"x x x −
.
Câu 41. Cho mệnh đề
( )
:Px
2
" , 1 0"x x x + +
. Mệnh đề phủ định của mệnh đề
( )
Px
là:
A.
2
" , 1 0"x x x + +
. B.
2
" , 1 0"x x x + +
.
C.
2
" , 1 0"x x x + +
. D.
"
2
, 1 0"x x x + +
.
Câu 42. Cho mệnh đề
2
“ : ”A x x x=
. Trong các mệnh đề sau, mệnh đề nào là phủ định của
mệnh đề
A
?
A.
2
“ : ”x x x
B.
2
“ : ”x x x
C.
2
“ : ”x x x
D.
2
“ : ”x x x
Câu 43. Cho mệnh đề “phương trình
2
4 4 0xx− + =
có nghiệm”. Mệnh đề phủ định của mệnh đề đã
cho và tính đúng, sai của mệnh đề phủ định là:
A. Phương trình
2
4 4 0xx− + =
có nghiệm. Đây là mệnh đề đúng.
B. Phương trình
2
4 4 0xx− + =
có nghiệm. Đây là mệnh đề sai.
C. Phương trình
2
4 4 0xx− + =
vô nghiệm. Đây là mệnh đề đúng.
D. Phương trình
2
4 4 0xx− + =
vô nghiệm. Đây là mệnh đề sai.
Câu 44. Cho mệnh đề
2
“ : ”A x x x=
. Trong các mệnh đề sau, mệnh đề nào là phủ định của
mệnh đề
A
?
A.
2
“ : ”x x x
. B.
2
“ : ”x x x
. C.
2
“ : ”x x x
. D.
2
“ : ”x x x
.
Câu 45. Cho mệnh đề
:A
“
2
, 7 0x x x − +
” Mệnh đề phủ định của
A
là:
A.
2
, 7 0x x x − +
. B.
2
, 7 0x x x − +
.
C. Không tồn tại
2
: 7 0x x x− +
. D.
2
, - 7 0x x x +
.
Câu 46. Cho
n
là số tự nhiên mệnh đề phủ định của mệnh đề nào sau đây đúng?
A.
:P
”
( )
,1n n n +
không là số chính phương”.
B.
:Q
”
( )
,1n n n +
là số chẵn”.
C.
:R
”
( )( )
, 1 2n n n n + +
là số chẵn”.
D.
:M
”
( )( )
, 1 2n n n n + +
không chia hết cho 6”.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 47. Cho mệnh đề: “Nếu
2ab+
thì một trong hai số
a
và
b
nhỏ hơn 1”. Phát biểu mệnh đề
trên bằng cách sử dụng khái niệm “điều kiện đủ”.
A.
2ab+
là điều kiện đủ để một trong hai số
a
và
b
nhỏ hơn 1.
B. Một trong hai số
a
và
b
nhỏ hơn 1 là điều kiện đủ để
2ab+
.
C. Từ
2ab+
suy ra một trong hai số
a
và
b
nhỏ hơn 1
D. Tất cả các câu trên đều đúng.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 48. Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh
đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?
A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong.
B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau.
C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.
D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.
Câu 49. Cho mệnh đề : “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng
nhau”. Phát biểu mệnh đề trên bằng cách sử dụng khái niệm “điều kiện cần”.
A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau.
B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân .
C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo bằng nhau.
D. Cả a, b đều đúng.
Câu 50. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?
A. Tam giác cân có hai cạnh bằng nhau.
B.
x
chia hết cho 6 thì
x
chia hết cho 2 và 3.
C.
ABCD
là hình bình hành thì
AB
song song với
CD
.
D.
ABCD
là hình chữ nhật thì
90 .A B C= = =
Câu 51. Mệnh đề nào dưới đây sai ?
A. Tứ giác
ABCD
là hình chữ nhật khi và chỉ khi
ABCD
có ba góc vuông.
B. Tứ giác
ABCD
là hình bình hành khi và chỉ khi
ABCD
có hai cạnh đối song song và
bằng nhau.
C. Tứ giác
ABCD
là hình thoi khi và chỉ khi
ABCD
có hai đường chéo vuông góc với
nhau tại trung điểm mỗi đường.
D. Tứ giác
ABCD
là hình vuông khi và chỉ khi
ABCD
có bốn góc vuông.
Câu 52. Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
A. Nếu số nguyên n có chữ số tận cùng là 5 thì số nguyên n chia hết cho 5.
B. Nếu tứ giác
ABCD
có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác
ABCD
là hình bình hành.
C. Nếu tứ giác
ABCD
là hình chữ nhật thì tứ giác
ABCD
có hai đường chéo bằng nhau.
D. Nếu tứ giác
ABCD
là hình thoi thì tứ giác
ABCD
có hai đường chéo vuông góc với
nhau.
Câu 53: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?
A. Nếu tổng hai số
2ab+
thì có ít nhất có một số lớn hơn 1.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
B. Trong một tam giác cân hai đường cao bằng nhau.
C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.
D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.
Câu 54: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?
A. “
ABC
là tam giác đều
ABC
cân”.
B. “
ABC
là tam giác đều
ABC
cân và có 1 góc
0
60
”.
C. “
ABC
là tam giác đều
ABC
là tam giác có ba cạnh bằng nhau”.
D. “
ABC
là tam giác đều
ABC
có hai góc
0
60
”.
Câu 55: Cho
a
. Mệnh đề nào dưới đây đúng?
A.
2a
và
3a
6a
. B.
39aa
.
C.
24aa
. D.
3a
và
6a
thì
18a
.
Câu 56: Mệnh đề nào dưới đây sai?
A. Tứ giác
ABCD
là hình chữ nhật khi và chỉ khi
ABCD
có ba góc vuông.
B. Tứ giác
ABCD
là hình bình hành khi và chỉ khi
ABCD
có hai cạnh đối song song và
bằng nhau.
C. Tứ giác
ABCD
là hình thoi khi và chỉ khi
ABCD
có hai đường chéo vuông góc với
nhau tại trung điểm mỗi đường.
D. Tứ giác
ABCD
là hình vuông khi và chỉ khi
ABCD
có bốn góc vuông.
Câu 57: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?
A. Nếu
a
và
b
cùng chia hết cho
c
thì
ab+
chia hết cho
c
.
B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.
C. Nếu
a
chia hết cho
3
thì
a
chia hết cho
9
.
D. Nếu một số tận cùng bằng
0
thì số đó chia hết cho
5
.
Câu 58: Trong các mệnh đề sau, mệnh đề nào không phải là định lí?
A.
2
, xx
chia hết cho
3
x
chia hết cho
3
.
B.
2
, xx
chia hết cho
6
x
chia hết cho
3
.
C.
2
, xx
chia hết cho
9
x
chia hết cho
9
.
D.
, xx
chia hết cho
4
và
6
x
chia hết cho
12
.
Câu 59: Trong các mệnh đề sau, mệnh đề nào SAI?
A. Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
B. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có cặp cạnh tương ứng bằng
nhau.
C. Một tam giác là tam giác vuông khi và chỉ khi có một góc bằng tổng của hai góc còn
lại.
D. Một tứ giác nội tiếp được đường tròn khi và chỉ khi tổng hai góc đối diện bằng 180
0
.
Nhắn tin Zalo