SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT HÀ NỘI N
ĂM HỌC: 20 19 – 2020 ĐỀ CHÍNH THỨC Môn thi: TOÁN Ngày thi: 02/06/2019
Thời gian làm bài: 120 phút
Bài I (2,0 điểm) Cho hai biểu thức và với .
1) Tính giá trị của biểu thức khi . 2) Rút gọn biểu thức .
3) Tìm tất cả các giá trị nguyên của để biểu thức
đạt giá trị nguyên lớn nhất.
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai đội công nhân cùng làm chung một công việc thì sau ngày làm xong. Nếu
đội thứ nhất làm riêng trong ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó
trong ngày thì cả hai đội hoàn thành được
công việc. Hỏi mỗi đội làm riêng thì
trong bao nhiêu ngày mới xong công việc trên?
2) Một bồn nước inox có dạng một hình trụ với chiều cao và diện tích đáy là
. Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn nước).
Bài III (2,0 điểm) 1) Giải phương trình:
2) Trong mặt phẳng tọa độ , cho đường thẳng và parabol . a) Chứng minh luôn cắt
tại hai điểm phân biệt.
b) Tìm tất cả giá trị của m để cắt
tại hai điểm phân biệt có hoành độ thỏa mãn .
Bài IV (3,0 điểm) Cho tam giác có ba góc nhọn (
) nội tiếp đường tròn . Hai đường cao và của tam giác cắt nhau tại điểm .
1) Chứng minh bốn điểm , , , cùng thuộc một đường tròn.
2) Chứng minh đường thẳng
vuông góc với đường thẳng .
3) Gọi là trung điểm của đoạn thẳng . Đường thẳng cắt đường thẳng
tại điểm , đường thẳng cắt đường thẳng
tại điểm . Chứng minh tam giác
đồng dạng với tam giác và đường thẳng song song với đường thẳng .
Bài V (0,5 điểm) Cho biểu thức , với
là các số thực thỏa mãn .
Tìm giá trị lớn nhất, giá trị nhỏ nhất của .
……………. Hết …………
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:………………………..
Số báo danh: ……………………
Họ, tên và chữ kí của cán bộ coi thi số 1:
Họ, tên và chữ kí của cán bộ coi thi số 2:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI TUYỂN SINH LỚP 10 THPT HÀ NỘI N
ĂM HỌC: 20 19 – 2020 ĐỀ CHÍNH THỨC
ĐÁP ÁN – THANG ĐIỂM Môn thi: TOÁN Bài Ý Nội dung Điểm Bài I
1) Tính giá trị của biểu thức khi . 0,5 2,0 điểm Với
(thỏa mãn điều kiện) thay vào ta có: 0,25 0,25 .
2) Rút gọn biểu thức . 1,0 Với , , ta có: 1,0 . . .
Đề chính thức Toán vào 10 Hà Nội năm 2019 - 2020
1.2 K
603 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu tuyển tập đề thi môn Toán vào 10 TP Hà Nội mới nhất qua các năm 2022 - 2023 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán vào 10.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1206 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Ôn vào 10
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NỘI
ĐỀ CHÍNH THỨC
KÌ THI TUYỂN SINH LỚP 10 THPT
NĂM HỌC: 20 19 – 2020
Môn thi: TOÁN
Ngày thi: 02/06/2019
Thời gian làm bài: 120 phút
Bài I (2,0 điểm)
Cho hai biểu thức và với
.
1) Tính giá trị của biểu thức khi .
2) Rút gọn biểu thức .
3) Tìm tất cả các giá trị nguyên của để biểu thức đạt giá trị nguyên lớn
nhất.
Bài II (2,5 điểm)
1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Hai đội công nhân cùng làm chung một công việc thì sau ngày làm xong. Nếu
đội thứ nhất làm riêng trong ngày rồi dừng lại và đội thứ hai làm tiếp công việc đó
trong ngày thì cả hai đội hoàn thành được công việc. Hỏi mỗi đội làm riêng thì
trong bao nhiêu ngày mới xong công việc trên?
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
2) Một bồn nước inox có dạng một hình trụ với chiều cao và diện tích đáy
là . Hỏi bồn nước này đựng đầy được bao nhiêu mét khối nước? (Bỏ qua bề dày
của bồn nước).
Bài III (2,0 điểm)
1) Giải phương trình:
2) Trong mặt phẳng tọa độ , cho đường thẳng và parabol
.
a) Chứng minh luôn cắt tại hai điểm phân biệt.
b) Tìm tất cả giá trị của m để cắt tại hai điểm phân biệt có hoành độ
thỏa mãn .
Bài IV (3,0 điểm)
Cho tam giác có ba góc nhọn ( ) nội tiếp đường tròn . Hai
đường cao và của tam giác cắt nhau tại điểm .
1) Chứng minh bốn điểm , , , cùng thuộc một đường tròn.
2) Chứng minh đường thẳng vuông góc với đường thẳng .
3) Gọi là trung điểm của đoạn thẳng . Đường thẳng cắt đường thẳng
tại điểm , đường thẳng cắt đường thẳng tại điểm . Chứng minh tam
giác đồng dạng với tam giác và đường thẳng song song với đường
thẳng .
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Bài V (0,5 điểm)
Cho biểu thức , với là các số thực thỏa mãn .
Tìm giá trị lớn nhất, giá trị nhỏ nhất của .
……………. Hết …………
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………….. Số báo danh: ……………………
Họ, tên và chữ kí của cán bộ coi thi số 1: Họ, tên và chữ kí của cán bộ coi thi số 2:
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NỘI
ĐỀ CHÍNH THỨC
KÌ THI TUYỂN SINH LỚP 10 THPT
NĂM HỌC: 20 19 – 2020
ĐÁP ÁN – THANG ĐIỂM
Môn thi: TOÁN
Bài Ý Nội dung Điểm
Bài I
2,0 điểm
1)
Tính giá trị của biểu thức khi .
0,5
Với (thỏa mãn điều kiện) thay vào ta có:
0,25
.
0,25
2)
Rút gọn biểu thức .
1,0
Với , , ta có:
.
.
.
1,0
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
.
.
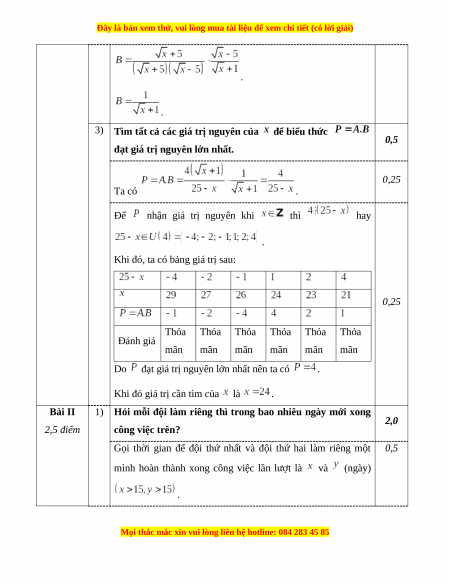
3)
Tìm tất cả các giá trị nguyên của để biểu thức
đạt giá trị nguyên lớn nhất.
0,5
Ta có .
0,25
Để nhận giá trị nguyên khi thì hay
.
Khi đó, ta có bảng giá trị sau:
Đánh giá
Thỏa
mãn
Thỏa
mãn
Thỏa
mãn
Thỏa
mãn
Thỏa
mãn
Thỏa
mãn
Do đạt giá trị nguyên lớn nhất nên ta có .
Khi đó giá trị cần tìm của là .
0,25
Bài II
2,5 điểm
1) Hỏi mỗi đội làm riêng thì trong bao nhiêu ngày mới xong
công việc trên?
2,0
Gọi thời gian để đội thứ nhất và đội thứ hai làm riêng một
mình hoàn thành xong công việc lần lượt là và (ngày)
.
0,5
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85