Đề thi HSG Vật Lí 10 Trường THPT Chuyên Nguyễn Tất Thành - Yên Bái

TRƯỜNG THPT CHUYÊN
KỲ THI HỌC SINH GIỎI CÁC TRƯỜNG THPT CHUYÊN
NGUYỄN TẤT THÀNH –YÊN BÁI
KHU VỰC DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ
(Đề thi gồm 03 trang)
LẦN THỨ XVI, NĂM 2024 ĐỀ THI ĐỀ XUẤT
ĐỀ THI MÔN: VẬT LÍ LỚP 10
Thời gian: 180 phút (Không kể thời gian giao đề)
Câu 1. Giữ một thanh theo chiều ngang ở đầu thanh. Để giữ nó đứng yên, bạn sẽ phải tác dụng lực tổng hợp
lên phần dưới và phần trên của nó. Các lực này có thể được xem như là sự chồng chất của một lực hướng lên
và một cặp lực trái dấu. Cái trước đảm bảo các lực tác dụng lên thanh được cân bằng, trong khi cái sau cung
cấp một mô-men lực, đảm bảo các mômen quay trên thanh được cân bằng. Vì mômen lực sinh ra từ một cặp
lực trái dấu nên nó không phụ thuộc vào việc chọn gốc tọa độ.
a. Xét một thanh có chiều dài l và khối lượng trên chiều dài λ. Mômen lực bạn phải tác dụng để giữ thanh
nằm ngang ở đầu của nó là bao nhiêu?
Giống như mỗi đoạn dây tác dụng lực căng lên các đoạn lân cận ở trạng thái cân bằng, mỗi đoạn của một
thanh rắn cũng tác dụng một mômen uốn lên các đoạn lân cận của nó. Đối với các thanh mỏng chịu tải nặng,
mômen lực này có thể là yếu tố hạn chế khiến chúng bị gãy.
Giả sử một thanh được đỡ ở cả hai đầu, sao cho nó tạo thành một cây cầu, như minh họa ở bên trái phía trên.
Giả sử các giá đỡ đơn giản nên chúng chỉ cung cấp lực hướng lên và không có mômen uốn. Ở trạng thái cân
bằng, mô men uốn sẽ xuất hiện khắp thanh. Độ lớn mômen uốn cực đại mà thanh có thể tác dụng tại bất kỳ
điểm nào mà không bị gãy là M0, và chiều dài của thanh là l. Cầu chịu tải trọng đều, có khối lượng theo
chiều dài là λ (bao gồm cả khối lượng của chính nó).
b. Tìm giá trị lớn nhất có thể có của λ trước khi cầu sập.
c. Bây giờ giả sử rằng một trụ đỡ vẫn ở đầu bên trái, trong khi trụ đỡ kia cách đầu bên trái một khoảng d > l /2,
như minh họa ở bên phải phía trên. Ở trạng thái cân bằng tĩnh, tìm mômen lực M(x0) ở khoảng cách x0 < d tính từ đầu bên trái.
d. Tìm giá trị d để tải trọng λ mà cây cầu có thể chịu được lớn nhất trước khi sập.
Câu 2. Các mẫu ô tô mới phải vượt qua các cuộc kiểm tra an toàn
trước khi xuất xưởng. Trong một cuộc kiểm tra ô tô nào đó, một trong M
ba nan hoa của bánh xe ô tô đã bị văng ra. Mặt cắt ngang của bánh xe
như Hình 2. Bánh xe có thể được coi là một đĩa bánh xe có bán kính A R0 120
trong và bán kính ngoài lần lượt là R O 0 và hai nan tương ứng
(giả sử rằng đĩa bánh xe có thể được coi là một đĩa hình khuyên đồng m R1
nhất, các nan hoa có thể được coi là các thanh mỏng đồng nhất) và khối B
lượng của mỗi nan là m. Khối lượng của bánh xe là . Bánh xe
được thả từ trạng thái đứng yên từ vị trí như hình a. Khi thả ra, phân Hình 2
giác của góc giữa hai nan hoa trên bánh xe nằm ngang, sau đó bánh xe
thực hiện chuyển động lăn thuần túy trên mặt đất bằng phẳng. Tính
a. Gia tốc góc của bánh xe khi nó được thả ra lần đầu.
b. Khi nan OB quay về vị trí thẳng đứng lần đầu tiên sau khi nhả, gia tốc góc của bánh xe, lực ma sát và lực
đỡ của mặt đất tác dụng lên bánh xe.
Câu 3. Một vệ tinh coi như chất điểm có khối lượng m, đang chuyển động trên một quỹ đạo tròn tâm o, bán
kính R quanh Trái đất có khối lượng M.
a. Chứng minh rằng tốc độ v của nó không đổi và tính v theo G, M, R. Suy ra chu kỳ T của nó?
b. Người ta muốn chuyển vệ tinh này sang một quỹ đạo tròn khác có bán kính R' > R, nằm trong cùng mặt
phẳng quỹ đạo trên. Muốn thế ở tại điểm A của quỹ đạo 1 người ta tăng tốc theo phương tiếp tuyến để nó
vạch ra một quỹ đạo elip có trục lớn AB (quỹ đạo 2), trong đó B là điểm năm trên đường tròn bán kính R '.
Hãy xác định các vận tốc v1 và v2 của vệ tinh tại các điểm A và B và năng lượng cần cung cấp cho vệ
tinh tại A để chuyển quỹ đạo?
c. Sau khi vệ tinh đi qua B người ta lại tăng tốc một lần nữa theo phương tiếp tuyến để nó vạch ra một
đường tròn bán kính R'. Tính tốc độ v' của vệ tinh trên quỹ đạo 3 và năng lượng cần cung cấp cho vệ
tinh để nó chuyển từ quỹ đạo 2 sang quỹ đạo 3?
Câu 4. Trong chu trình Carnot, một chất khí được nung nóng ở nhiệt độ không đổi TH và được làm lạnh ở
nhiệt độ không đổi TC. Hơn nữa, không có sự truyền nhiệt nào khác xảy ra và tất cả các bước khác của chu
trình đều có thể đảo ngược. Các định luật nhiệt động lực học phát biểu rằng bất kỳ chu trình nào như vậy
đều phải có hiệu suất η=W/Qin =1-(TC/TH). Dưới đây chúng ta sẽ khám phá hai động cơ nhiệt khác phục hồi
hiệu suất này trong những giới hạn nhất định.
a. Xét động cơ nhiệt sau đây có một mol khí đơn nguyên tử lý
tưởng. Khí bắt đầu ở nhiệt độ T0, áp suất P0 và thể tích V0 và trải
qua bốn bước thuận nghịch.
1. Khí giãn nở ở áp suất không đổi cho đến khi nhiệt độ của nó tăng lên (1+β)T0.
2. Khí giãn nở ở nhiệt độ không đổi cho đến khi áp suất của nó giảm xuống P0/α.
3. Khí co lại ở áp suất không đổi cho đến khi nhiệt độ của nó giảm xuống T0.
4. Khí co lại ở nhiệt độ không đổi cho đến khi áp suất của nó tăng trở lại P0.
a1. Những bước nào cần nhiệt để truyền cho khí? Đối với mỗi bước như vậy, hãy tính tổng lượng nhiệt đầu vào theo P0,V0, α và β.
a2. Trong những điều kiện nào trên α và β, chúng ta mong đợi hiệu suất của động cơ nhiệt này đạt tới hiệu
suất của chu trình Carnot làm việc ở cùng nhiệt độ tối đa và tối thiểu?
a3. Tìm hiệu suất của động cơ nhiệt này đối với α và β tổng quát.
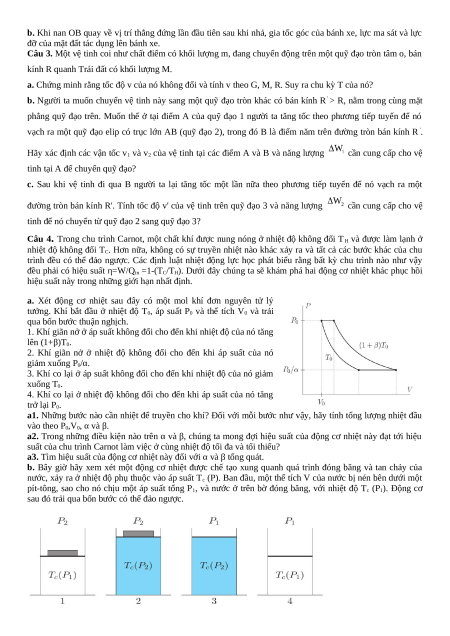
b. Bây giờ hãy xem xét một động cơ nhiệt được chế tạo xung quanh quá trình đóng băng và tan chảy của
nước, xảy ra ở nhiệt độ phụ thuộc vào áp suất Tc (P). Ban đầu, một thể tích V của nước bị nén bên dưới một
pít-tông, sao cho nó chịu một áp suất tổng P1, và nước ở trên bờ đóng băng, với nhiệt độ Tc (P1). Động cơ
sau đó trải qua bốn bước có thể đảo ngược.
1. Một vật nặng được đặt từ từ lên piston, nâng tổng áp suất lên P2.
2. Nước được làm lạnh đến nhiệt độ Tc (P2) và đông đặc.
3. Khối lượng từ từ được lấy ra khỏi piston, giảm áp suất xuống P1.
4. Nước đá được nung nóng trở lại nhiệt độ Tc(P1 ) và tan chảy.
Giả sử rằng nước và băng không thể nén được, có mật độ cố định ρw và ρi.
b1. Công thực hiện bởi công cụ này là bao nhiêu, xét theo P1, P2, V và mật độ?
b2. Giả sử nhiệt ẩn trên một đơn vị khối lượng L để làm tan băng là lớn, do đó sự đóng băng và tan chảy về
cơ bản chiếm toàn bộ quá trình truyền nhiệt trong chu trình. Hiệu suất của động cơ tính theo P 1, P2, L và mật độ là bao nhiêu?
b3. Vì chúng ta giả sử toàn bộ quá trình truyền nhiệt xảy ra trong quá trình nóng chảy hoặc đông đặc nên
chu trình này có cùng hiệu suất như chu trình Carnot. Trong giới hạn mà P1 và P2 rất gần nhau, hãy sử dụng
thực tế này để suy ra biểu thức cho d T /dP c theo Tc,L và mật độ.
Câu 5. Một cốc đo chứa nước được đặt trên cân điện tử như hình bên trái. Một khúc gỗ sau đó được thả nổi
trong nước. 3/4 thể tích của khúc gỗ chìm trong nước như hình bên phải. Thang đo trên cốc tính bằng mililít
và số đọc trên cân tính bằng gam.
Dựa vào số liệu từ hình vẽ hãy tính:
a. khối lượng 𝑚h của cốc rỗng;
b. lực đẩy F tác dụng lên khúc gỗ;
c. mật độ 𝜌 của khúc gỗ.
Mật độ của nước là 𝜌n=1g/cm3 và gia tốc của trái đất là Hướng dẫn Câu 1 Nội dung Thang điểm
Cân bằng mô men xoắn ở đầu thanh. Trọng lượng là λgl, tác dụng đều
dọc theo thanh nên mômen quay do trọng lực là λgl2/2. Điều này chỉ có
a thể được cân bằng bởi mômen uốn, nên nó là λgl2/2. 1,0
Đặt gốc tọa độ tại gối tựa bên trái, xét hệ gồm các điểm trên thanh tại
0<x<x0. Các lực bên ngoài là:
Một lực hướng lên λgl/2 ở đầu bên trái do giá đỡ bên trái. Trọng lượng λgx0.
Một lực hướng lên λg(x −l/2 0
) ở đầu bên phải do phần còn lại của thanh tác dụng.
Bây giờ hãy xem xét việc cân bằng mômen quay trên hệ thống
này về x=x0. Các mô men xoắn bên ngoài là:
Mô-men xoắn theo chiều kim đồng hồ λg l x0/2 do giá đỡ bên trái.
Mômen quay ngược chiều kim đồng hồ λg x20/2 do trọng lượng. b
Mô men uốn M(x0) do phần còn lại của thanh gây ra.
Để cân bằng mô men xoắn, mômen uốn phải bằng λg x2 λg l x λg x −l) 0,5 M ( x 0 − 0 = 0 ( x0 0 )= 2 2 2
Thanh có nhiều khả năng bị gãy ở nơi M lớn nhất, xảy ra ở trung tâm, do đó M =λg ¿¿ 0 Giải λ cho 0,5 8 M λ= 0 gl2 c
Để đơn giản hóa các biểu thức, hãy đặt W=λgl là trọng lượng của thanh.
Bằng cách cân bằng mô men quay quanh đầu bên trái của thanh, các
ngoại lực tác dụng lên toàn bộ thanh là
Một lực trọng lượng W.
Một lực hướng lên Wl/2d từ điểm tựa bên phải.
Lực hướng lên W - Wl/2d từ trụ đỡ bên trái.
Lưu ý rằng lý do chúng tôi chỉ định d>l/2 là vì nếu không, lực từ trụ bên
trái sẽ trở nên âm, trong trường hợp đó cây cầu sẽ nghiêng về bên phải.
Bây giờ hãy xem xét hệ thống bao gồm các điểm trên thanh có 0của thanh phải là
F =W (x0+ l −1) r l 2 d
Các mô men xoắn bên ngoài trên hệ thống này, về đầu bên trái, là
Mô-men xoắn ngược chiều kim đồng hồ W x20/2l do trọng lượng.
Mô men xoắn theo chiều kim đồng hồ F x
r 0 do phần còn lại của thanh gây ra.
Mô men uốn M(x0) do phần còn lại của thanh gây ra.