Bài tập cuối chương
Câu 1. Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với
mặt đất là 57°, khi đó độ nghiêng của chiếc thang đó so với bức tường là: A. 55°; B. 44°; C. 33°; D. 22°.
Câu 2. Cho tam giác MNP có 21M = 14N = 6P. Số đo góc N là: A. 30°; B. 45°; C. 60°; D. 105°. ︿ ︿
Câu 3. Cho tam giác ABC có B = 72 , C = 38 .
Tia phân giác góc A cắt cạnh BC tại D. Số đo góc ADB là: A. 73°; B. 55°; C. 67°; D. 35°.
Câu 4. Cho tam giác ABC có I là trung điểm của AB. Khẳng định nào sau đây là đúng? A. AC + BC ≤ 2CI; B. AC + BC > 2CI; C. AC + BC = CI;
D. AC + BC < 2CI.
Câu 5. Cho một tam giác cân có độ dài hai cạnh (không bằng nhau) là 2 cm và 5 cm.
Chu vi của tam giác đó là: A. 9 cm; B. 10 cm; C. 11 cm; D. 12 cm.
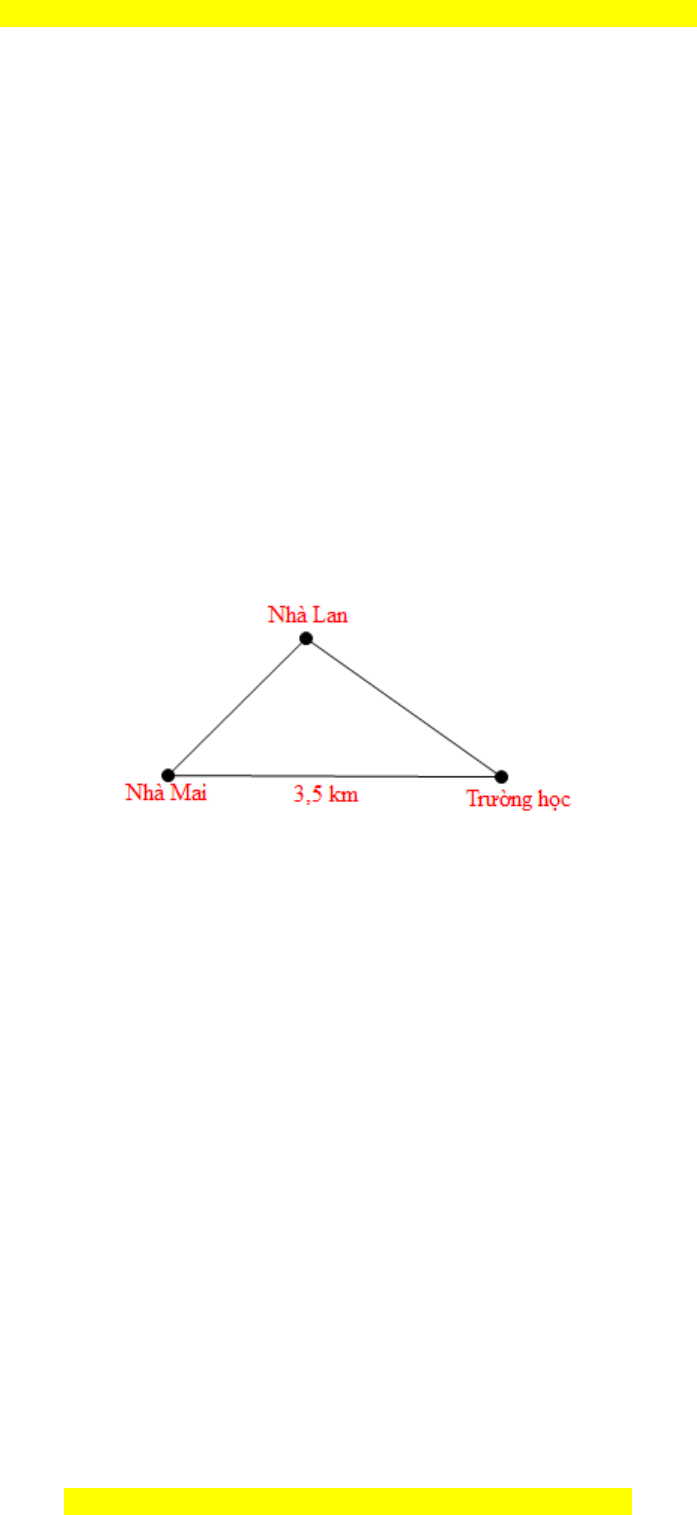
Câu 5. Ba vị trí của nhà Mai, nhà Lan và trường học được mô tả như hình vẽ dưới đây.
Trong buổi sáng hôm nay, Mai phải đến nhà Lan để lấy đồ trước khi đến trường.
Bạn Mai nói rằng tổng quãng đường mà Mai đã đi khoảng 3 km.
Bạn Lan nói rằng tổng quãng đường mà Mai đã đi khoảng 4 km.
Bạn Minh nói rằng tổng quãng đường mà Mai đã đi khoảng 5 km.
Chọn khẳng định đúng: A. Chỉ bạn Mai nói sai; B. Chỉ bạn Lan nói sai;
C. Bạn Lan và Minh nói sai. D. Cả ba bạn nói sai.
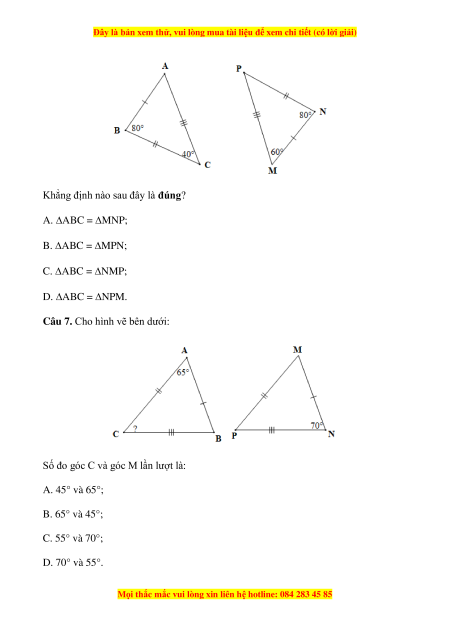
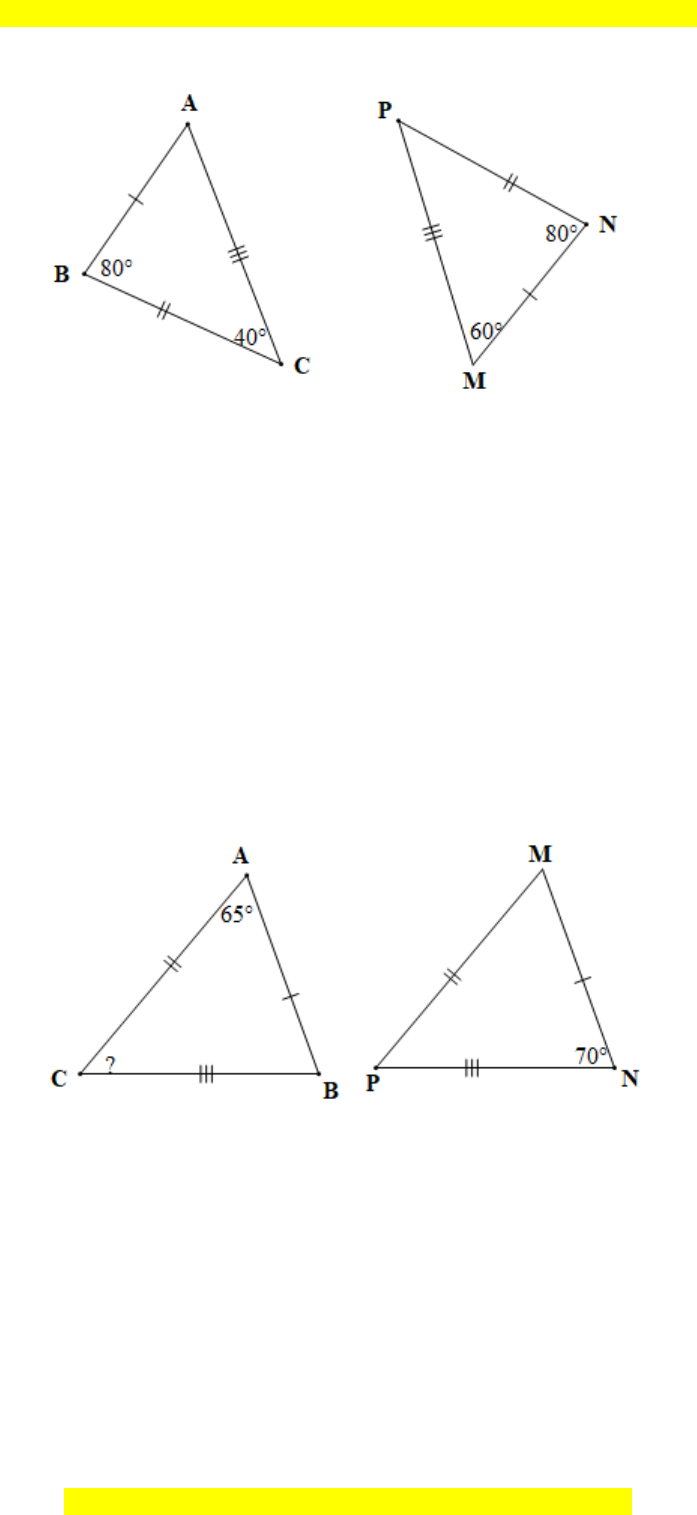
Câu 6. Cho hai tam giác ABC và MNP như hình vẽ dưới đây:
Khẳng định nào sau đây là đúng? A. ABC = MNP; B. ABC = MPN; C. ABC = NMP; D. ABC = NPM.
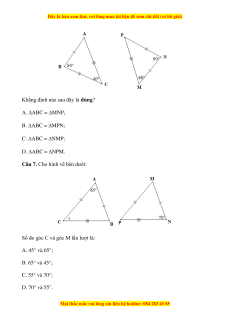
Câu 7. Cho hình vẽ bên dưới:
Số đo góc C và góc M lần lượt là: A. 45° và 65°; B. 65° và 45°; C. 55° và 70°; D. 70° và 55°.
Câu 8. Cho tam giác MNP có MN < MP. Lấy điểm I trên cạnh MP sao cho MN = PI.
Gọi H là điểm sao cho HM = HP, HN = HI.
Khẳng định nào sau đây là đúng ? A. MNH = PIH; B. MNH = PHI; C. MNH = HPI ; D. MHN = HIP .
Câu 9. Qua trung điểm H của đoạn thẳng BC, kẻ đường thẳng vuông góc với BC, trên
đường thẳng vuông góc đó lấy hai điểm A và I. Nối CA, AB, IB, IC. Phát biểu nào sau
đây là đúng nhất: A. ABH = ACH; B. IBH = ICH; C. BAI = CAI;
D. Cả A, B, C đều đúng.
Câu 10. Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F
và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là: A. 45°; B. 90°; C. 60°; D. 100°.
Câu 11. Cho hình vẽ sau:
Trắc nghiệm Bài tập cuối chương 7 Toán 7 Cánh diều
470
235 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Bộ câu hỏi trắc nghiệm Toán 7 Cánh diều học kì 2 mới nhất nhằm giúp Giáo viên có thêm tài liệu tham khảo Trắc nghiệm Toán lớp 7.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(470 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 7
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài tập cuối chương
Câu 1. Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với
mặt đất là 57°, khi đó độ nghiêng của chiếc thang đó so với bức tường là:
A. 55°;
B. 44°;
C. 33°;
D. 22°.
Câu 2. Cho tam giác MNP có
21M 14N 6P.==
Số đo góc N là:
A. 30°;
B. 45°;
C. 60°;
D. 105°.
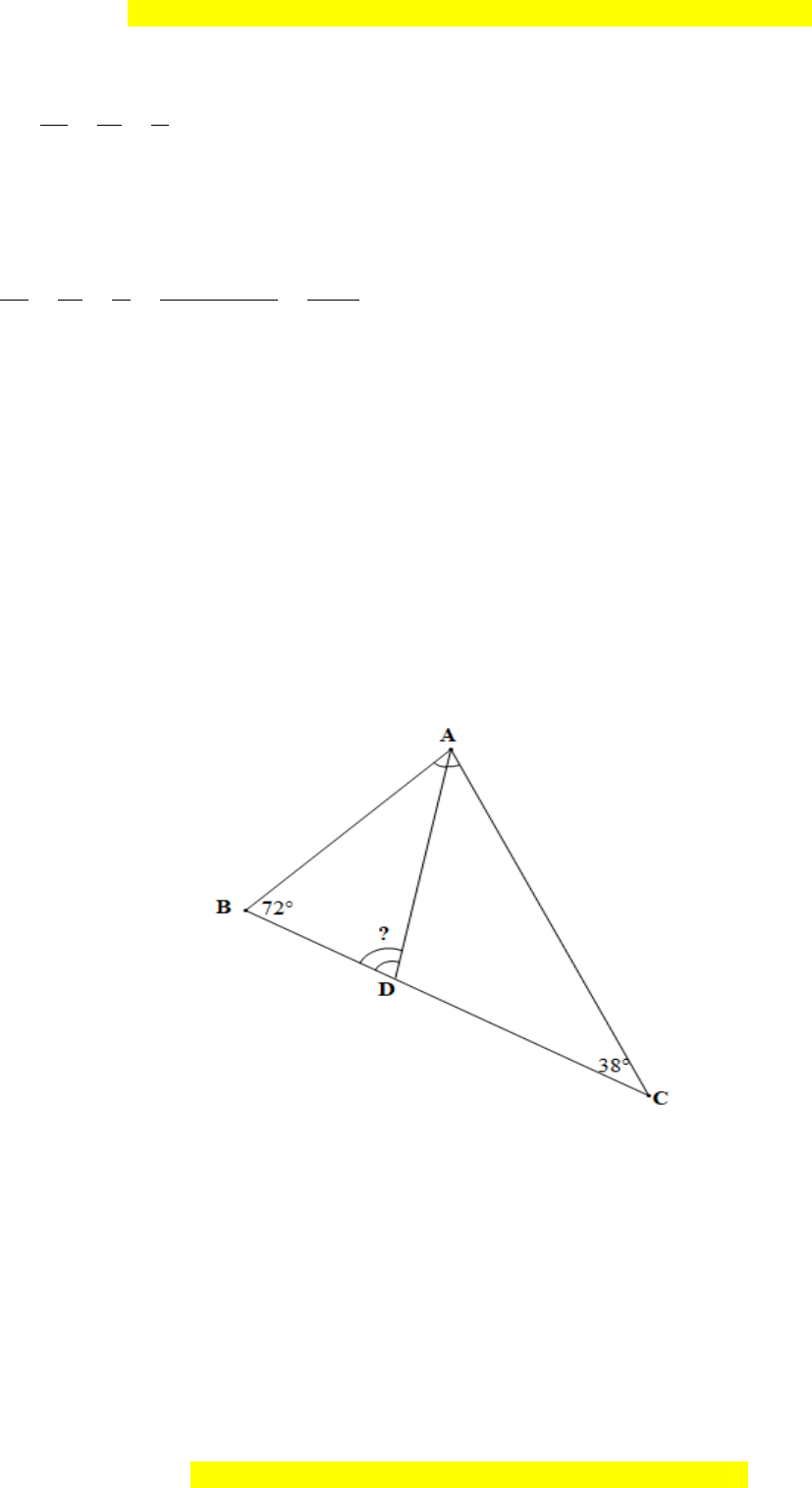
Câu 3. Cho tam giác ABC có
B 72 ,C 38 .= =
︿︿
Tia phân giác góc A cắt cạnh BC tại
D. Số đo góc ADB là:
A. 73°;
B. 55°;
C. 67°;
D. 35°.
Câu 4. Cho tam giác ABC có I là trung điểm của AB. Khẳng định nào sau đây là đúng?
A. AC + BC ≤ 2CI;
B. AC + BC > 2CI;
C. AC + BC = CI;
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
D. AC + BC < 2CI.
Câu 5. Cho một tam giác cân có độ dài hai cạnh (không bằng nhau) là 2 cm và 5 cm.
Chu vi của tam giác đó là:
A. 9 cm;
B. 10 cm;
C. 11 cm;
D. 12 cm.
Câu 5. Ba vị trí của nhà Mai, nhà Lan và trường học được mô tả như hình vẽ dưới đây.
Trong buổi sáng hôm nay, Mai phải đến nhà Lan để lấy đồ trước khi đến trường.
Bạn Mai nói rằng tổng quãng đường mà Mai đã đi khoảng 3 km.
Bạn Lan nói rằng tổng quãng đường mà Mai đã đi khoảng 4 km.
Bạn Minh nói rằng tổng quãng đường mà Mai đã đi khoảng 5 km.
Chọn khẳng định đúng:
A. Chỉ bạn Mai nói sai;
B. Chỉ bạn Lan nói sai;
C. Bạn Lan và Minh nói sai.
D. Cả ba bạn nói sai.
Câu 6. Cho hai tam giác ABC và MNP như hình vẽ dưới đây:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Khẳng định nào sau đây là đúng?
A. ABC = MNP;
B. ABC = MPN;
C. ABC = NMP;
D. ABC = NPM.
Câu 7. Cho hình vẽ bên dưới:
Số đo góc C và góc M lần lượt là:
A. 45° và 65°;
B. 65° và 45°;
C. 55° và 70°;
D. 70° và 55°.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 8. Cho tam giác MNP có MN < MP. Lấy điểm I trên cạnh MP sao cho MN = PI.
Gọi H là điểm sao cho HM = HP, HN = HI.
Khẳng định nào sau đây là đúng ?
A. MNH = PIH;
B. MNH = PHI;
C.
MNH HPI=
;
D.
MHN HIP=
.
Câu 9. Qua trung điểm H của đoạn thẳng BC, kẻ đường thẳng vuông góc với BC, trên
đường thẳng vuông góc đó lấy hai điểm A và I. Nối CA, AB, IB, IC. Phát biểu nào sau
đây là đúng nhất:
A. ABH = ACH;
B. IBH = ICH;
C. BAI = CAI;
D. Cả A, B, C đều đúng.
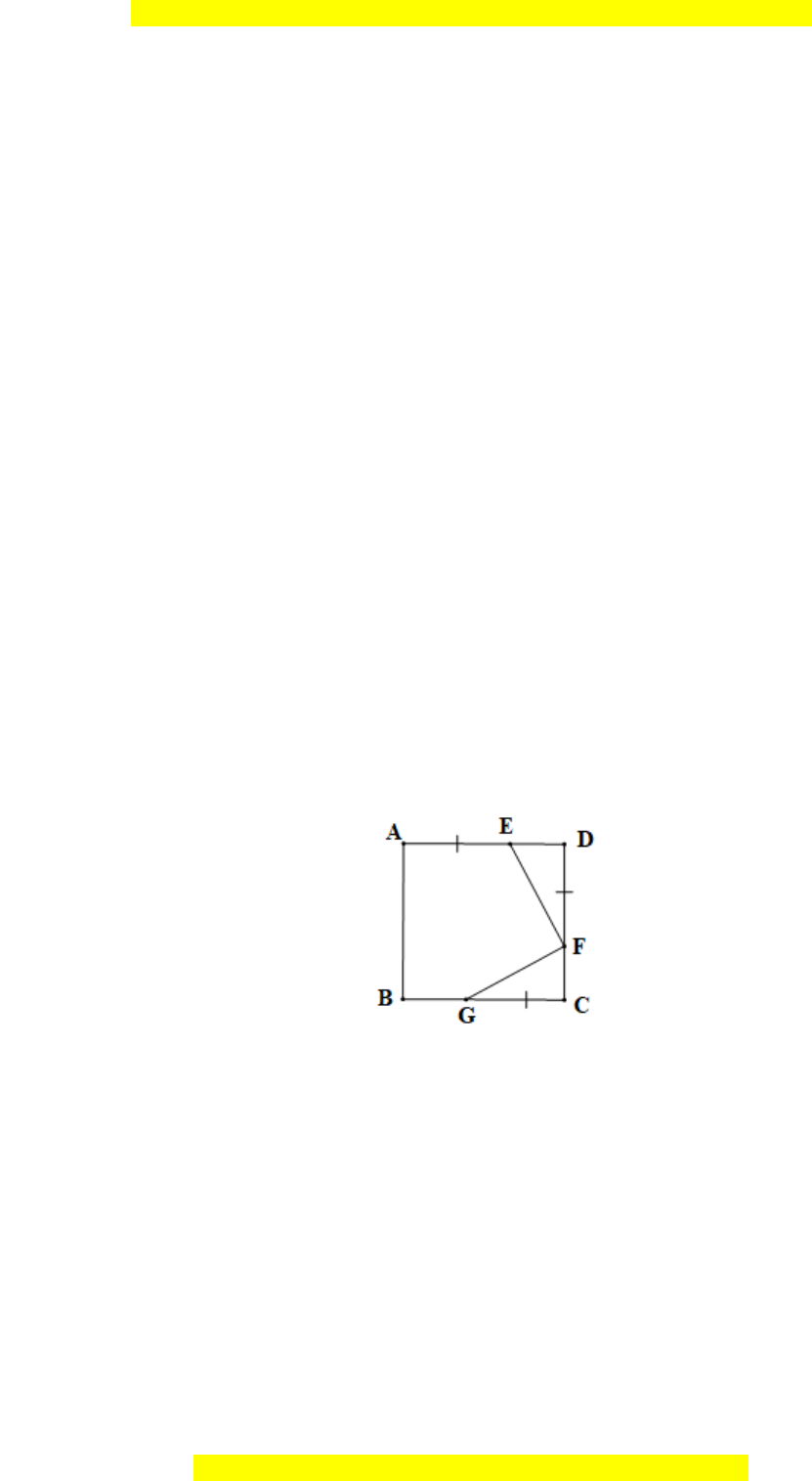
Câu 10. Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F
và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:
A. 45°;
B. 90°;
C. 60°;
D. 100°.
Câu 11. Cho hình vẽ sau:

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Biết CH = 3,5 cm. Số đo cạnh DK là:
A. 2,5 cm;
B. 3,5 cm;
C. 4 cm;
D. 4,5 cm.
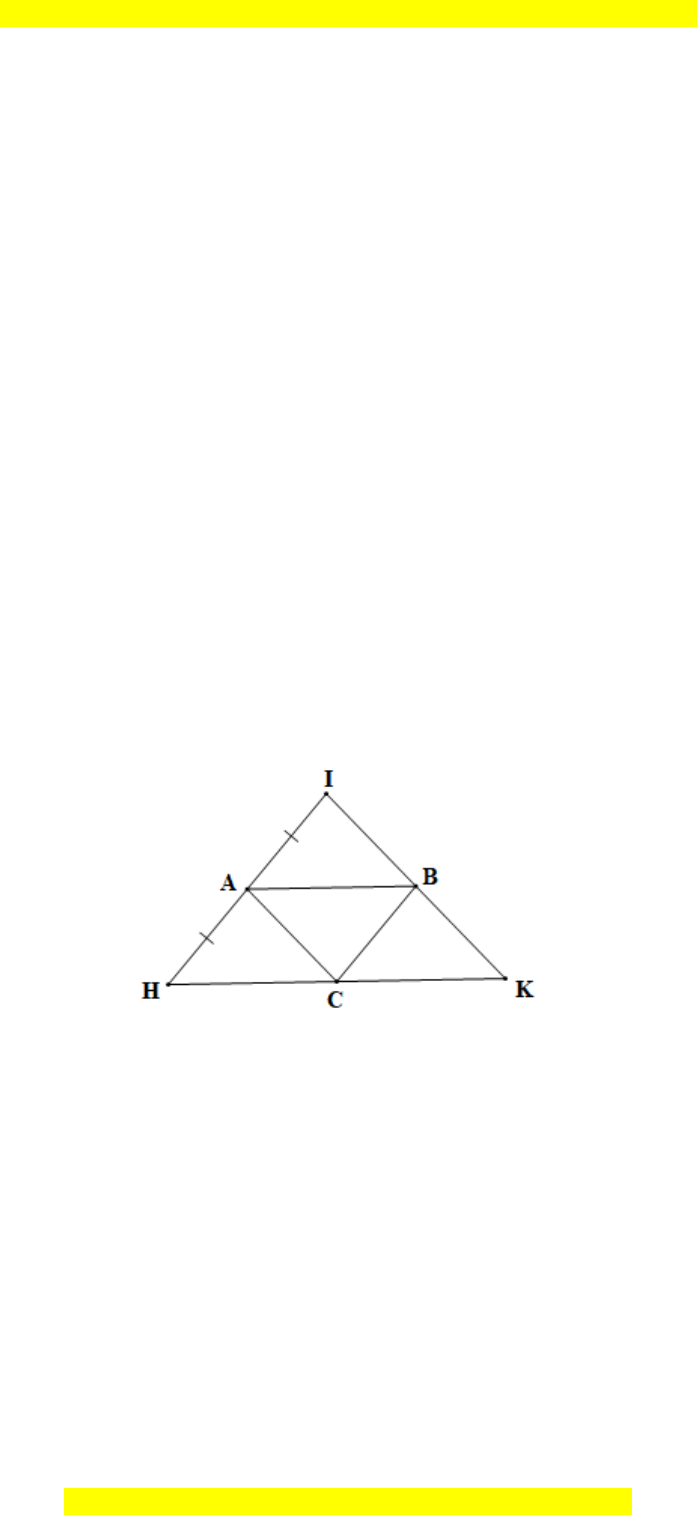
Câu 12. Cho tam giác HIK, A là trung điểm của IH. Đường thẳng qua A và song song
với HK cắt IK tại B. Đường thẳng qua B và song song với IH cắt HK tại C. Khẳng định
nào sau đây là đúng nhất ?
A. CH = KC;
B. ABI = CKB;
C. AI = BC;
D. Cả A, B , C đều đúng.
Câu 13. Cho ∆ABC vuông tại A có
C 30=
. Kẻ AH ⊥ BC tại H và tia phân giác AD
của
HAC
(D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia
HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?
A. ∆ADH = ∆ADE;
B. DE ⊥ AC;
C. ∆ACF đều;

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
D. Cả A, B, C đều đúng.
Câu 14. Cho hình vẽ sau:
Biết AM = 3 cm. Độ dài đoạn thẳng GM là:
A. 1 cm;
B. 2 cm;
C. 3 cm;
D. 4,5 cm.
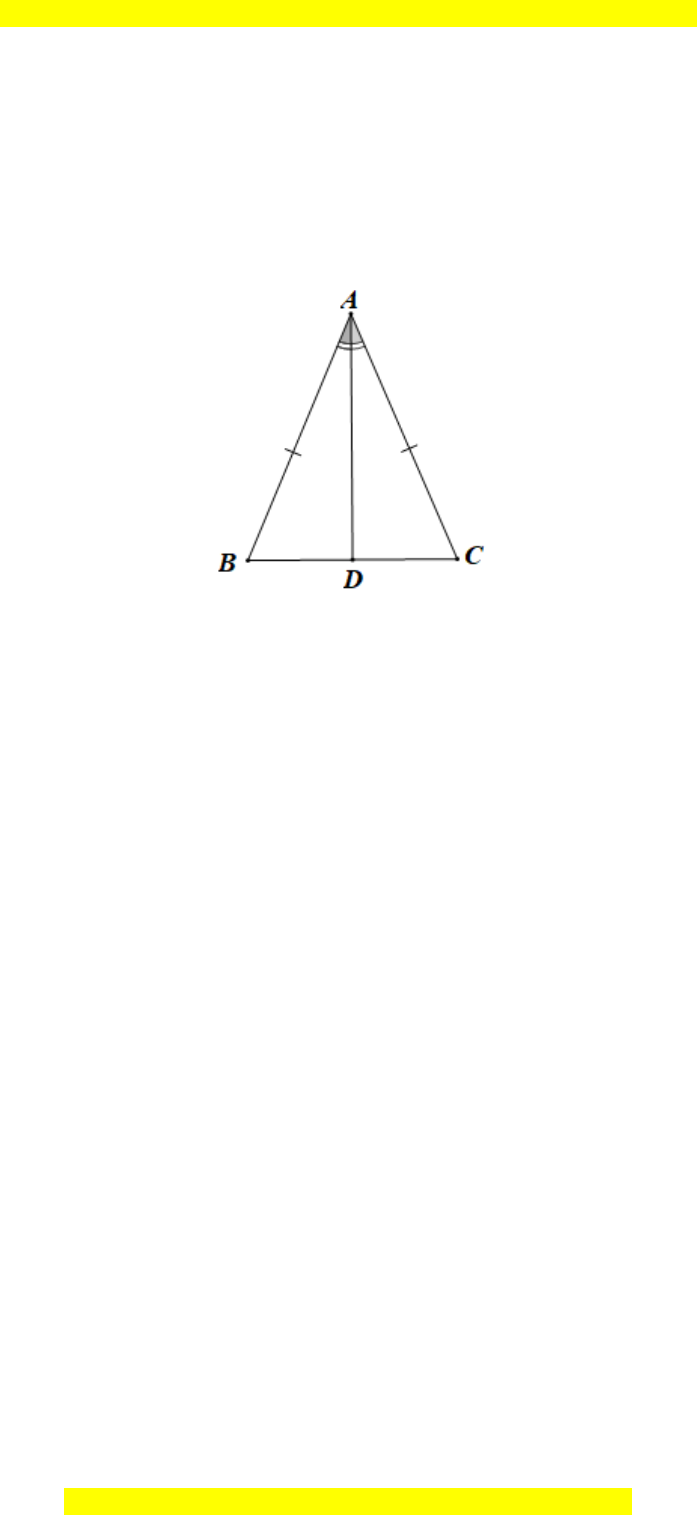
Câu 15. Cho ∆ABC cân tại A, tia phân giác trong của
A
cắt BC tại D. Khẳng định
nào dưới đây sai?
A. D là trung điểm BC;
B.
ABC CAD 90+ =
;
C. ∆ADB = ∆ADC;
D.
ABC ADC 180+ =
.
Câu 16. Giao điểm của ba đường trung tuyến trong một tam giác được gọi là gì?
A. Điểm cách đều ba đỉnh của tam giác đó;
B. Trọng tâm;
C. Điểm cách đều ba cạnh của tam giác đó;
D. Trực tâm.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 17. Trong một tam giác, trực tâm là giao điểm của ba đường gì?
A. Trung trực;
B. Phân giác;
C. Trung tuyến;
D. Đường cao.
Câu 18. Cho các phát biểu:
(I) Ba đường trung tuyến của một tam giác đồng quy tại một điểm.
(II) Ba đường phân giác của một tam giác đồng quy tại một điểm.
(III) Ba đường trung trực của một tam giác đồng quy tại một điểm.
(IV) Ba đường cao của một tam giác đồng quy tại một điểm.
Số các phát biểu đúng là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu 19. Cho ∆ABC vuông tại A. Trực tâm của ∆ABC là điểm nào?
A. Điểm A;
B. Điểm B;
C. Điểm C;
D. Không có trực tâm.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 20. Cho đoạn thẳng PQ. Gọi A và B là hai điểm thuộc đường trung trực của
đoạn PQ sao cho AP = 6 cm, BQ = 8 cm. Gọi I là giao điểm của PQ và AB. Khẳng
định nào sau đây đúng nhất?
A. I là trung điểm của PQ;
B. AQ < BQ;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
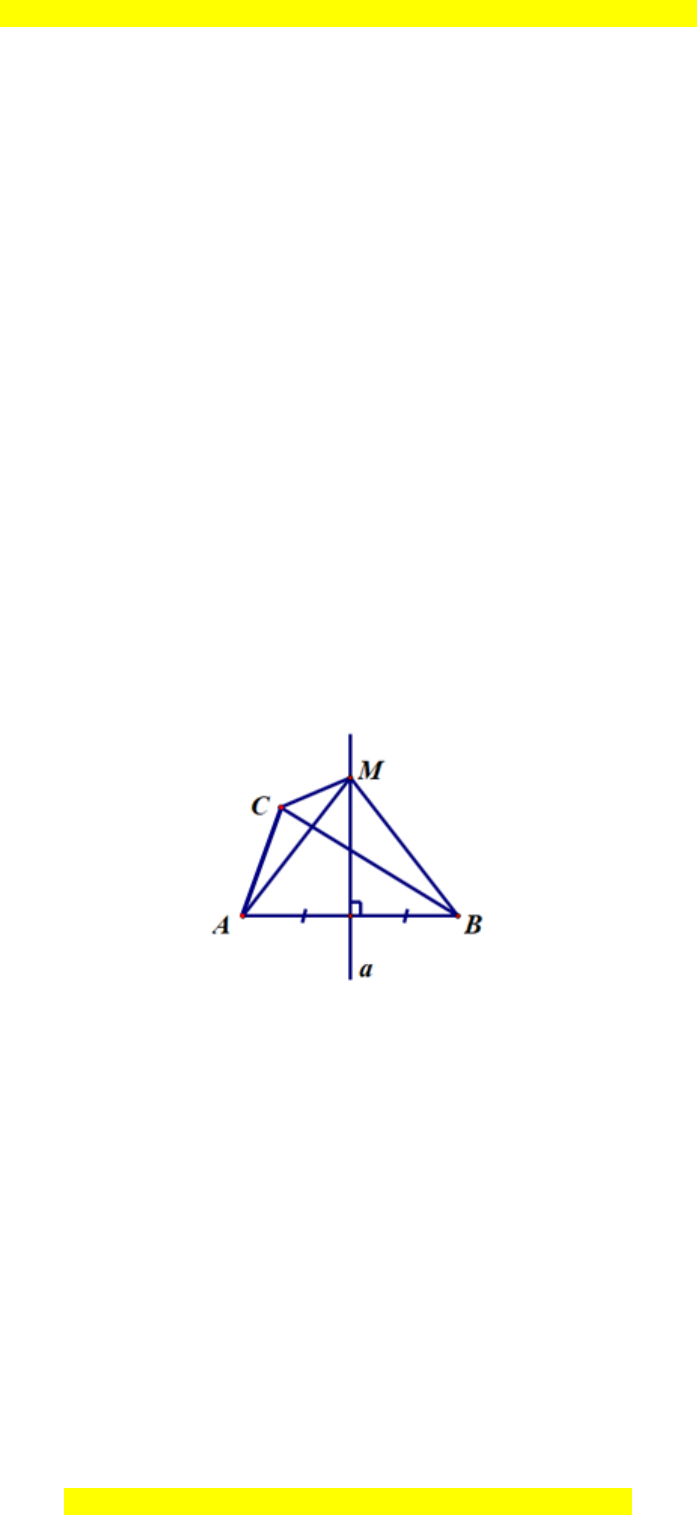
Câu 21. Cho tam giác ABC (AC < BC), a là đường trung trực của đoạn thẳng AB.
Lấy điểm M (M khác trung điểm của AB) nằm trên đường thẳng a.
So sánh độ dài của MA + MC với độ dài đoạn BC.
A. MA + MC < BC;
B. MA + MC > BC;
C. MA + MC = BC;
D. Không thể so sánh được.
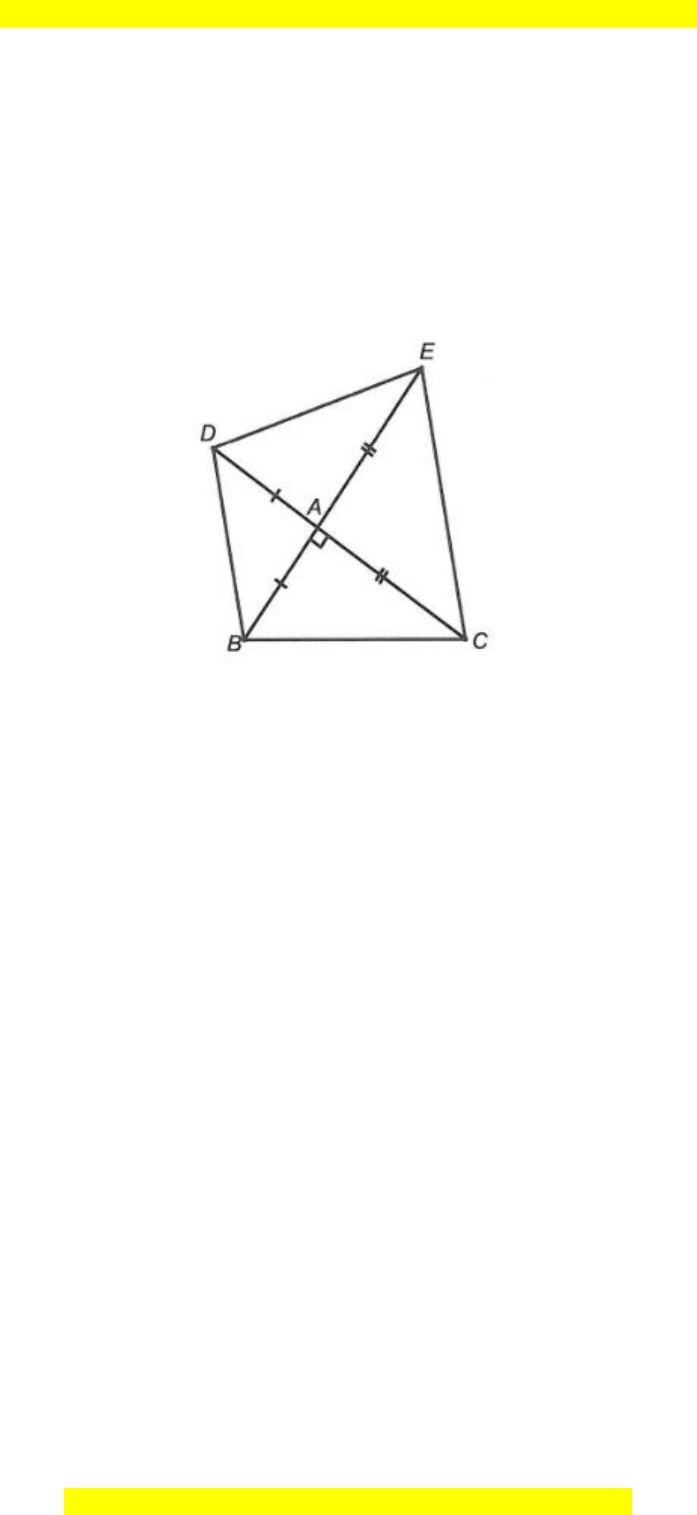
Câu 22. ∆ABC có
B 90
. Gọi O là trung điểm của BC. Vẽ BD ⊥ AO, CE ⊥ AO
(D, E thuộc đường thẳng AO). So sánh AB và
AD AE
2
+
.
A.
AD AE
AB
2
+
;
B.
AD AE
AB
2
+
=
;
C.
AD AE
AB
2
+
;
D. Không thể so sánh được.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 23. Cho ∆ABC vuông tại A (AB < AC). Trên tia đối của tia AC lấy điểm D sao
cho AD = AB. Trên tia đối của tia AB lấy điểm E sao cho AE = AC. Khẳng định nào
sau đây đúng nhất?
A. BC = DE;
B. ∆ABD vuông cân;
C. BD // CE;
D. Cả A, B, C đều đúng.
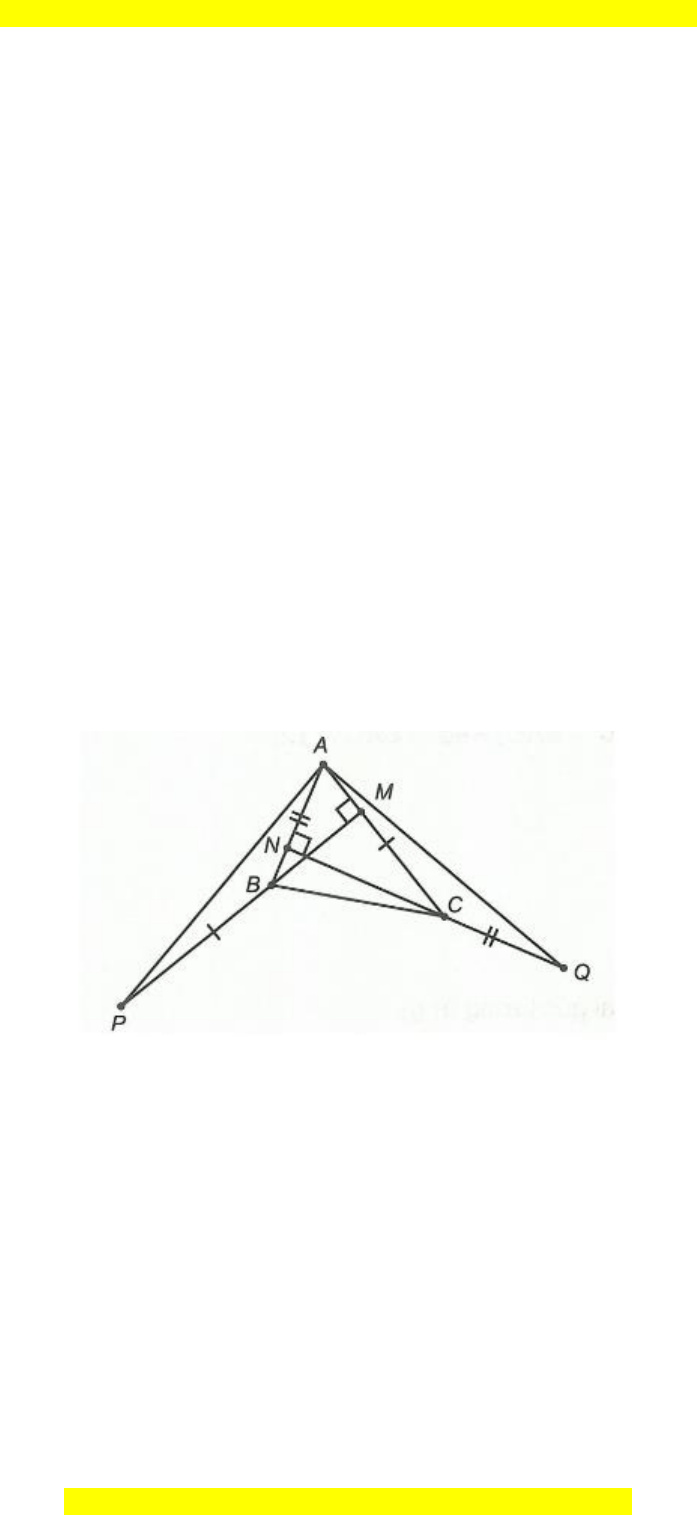
Câu 24. Cho ∆ABC nhọn, hai đường cao BM và CN. Trên tia đối của tia BM, lấy
điểm P sao cho BP = AC. Trên tia đối của tia CN, lấy điểm Q sao cho CQ = AB.
Khẳng định nào sau đây đúng nhất?
A. ∆APQ vuông cân tại A;
B. ∆BAP = ∆CQA;
C.
PBA ACQ=
;
D. Cả A, B, C đều đúng.
Câu 25. Cho ∆ABC vuông cân tại A. Trên cạnh AB lấy điểm D bất kì (D ≠ A, B),
trên tia đối của tia AC, lấy điểm E sao cho AD = AE. Khẳng định nào sau đây đúng
nhất?
A.
ACD ABE=
;
B. CD ⊥ BE;
C. D là trực tâm của ∆BEC;
D. Cả A, B, C đều đúng.
Câu 26. Cho ∆ABC có AB < AC, lấy điểm E trên cạnh CA sao cho CE = BA. Các
đường trung trực của các đoạn thẳng BE và CA cắt nhau tại I. Chọn khẳng định sai.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. ∆AIB = ∆EIC;
B. AI là đường phân giác của ∆ABC;
C.
IAC IAB=
;
D. IA = IC.
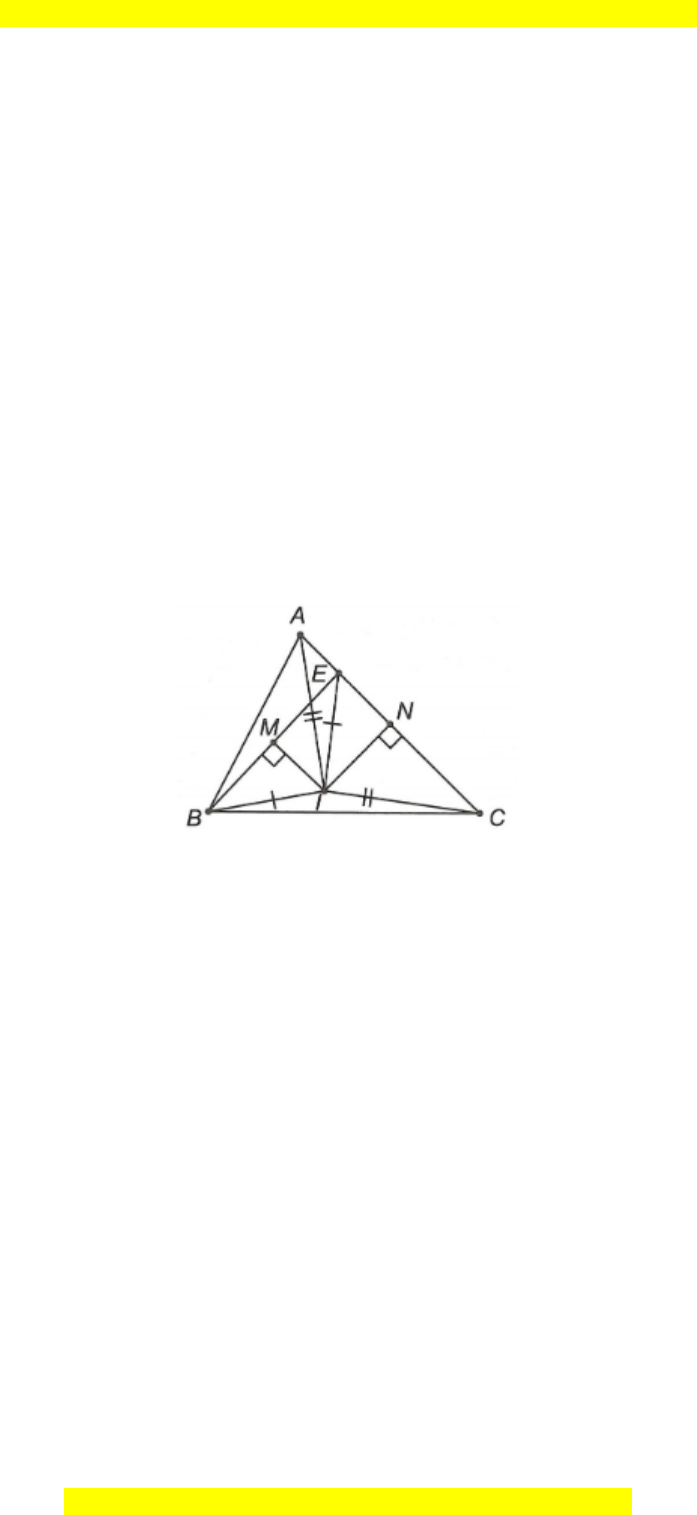
Câu 27. Cho ∆ABC có
B 75=
,
C 45=
. Vẽ đường trung trực d của cạnh BC và d
cắt BC tại M. Gọi E là điểm thuộc d (E nằm bên trong ∆ABC) sao cho
EBC 30=
.
Khẳng định nào sau đây đúng nhất?
A. ∆BEC cân tại E;
B.
BAC ABE ACE=+
;
C.
AEB 90=
;
D. Cả A, B, C đều đúng.
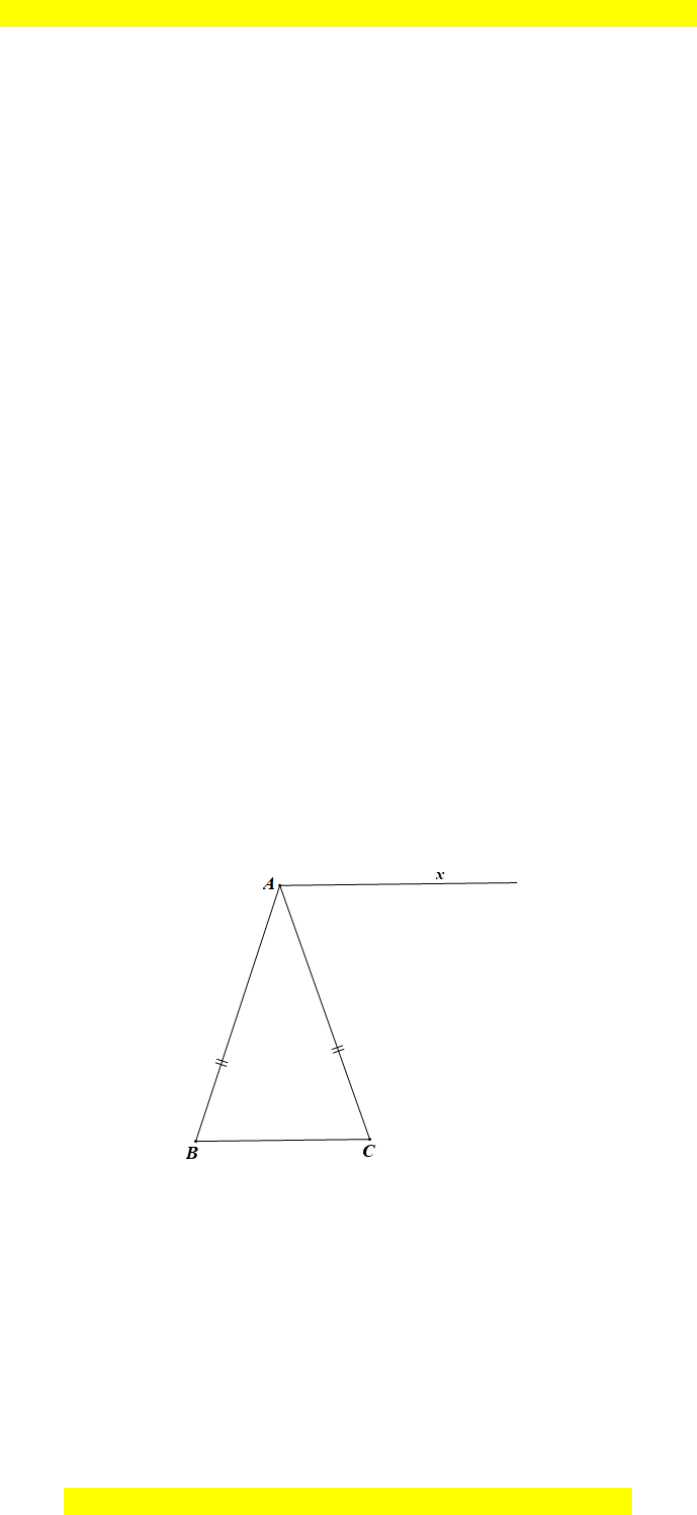
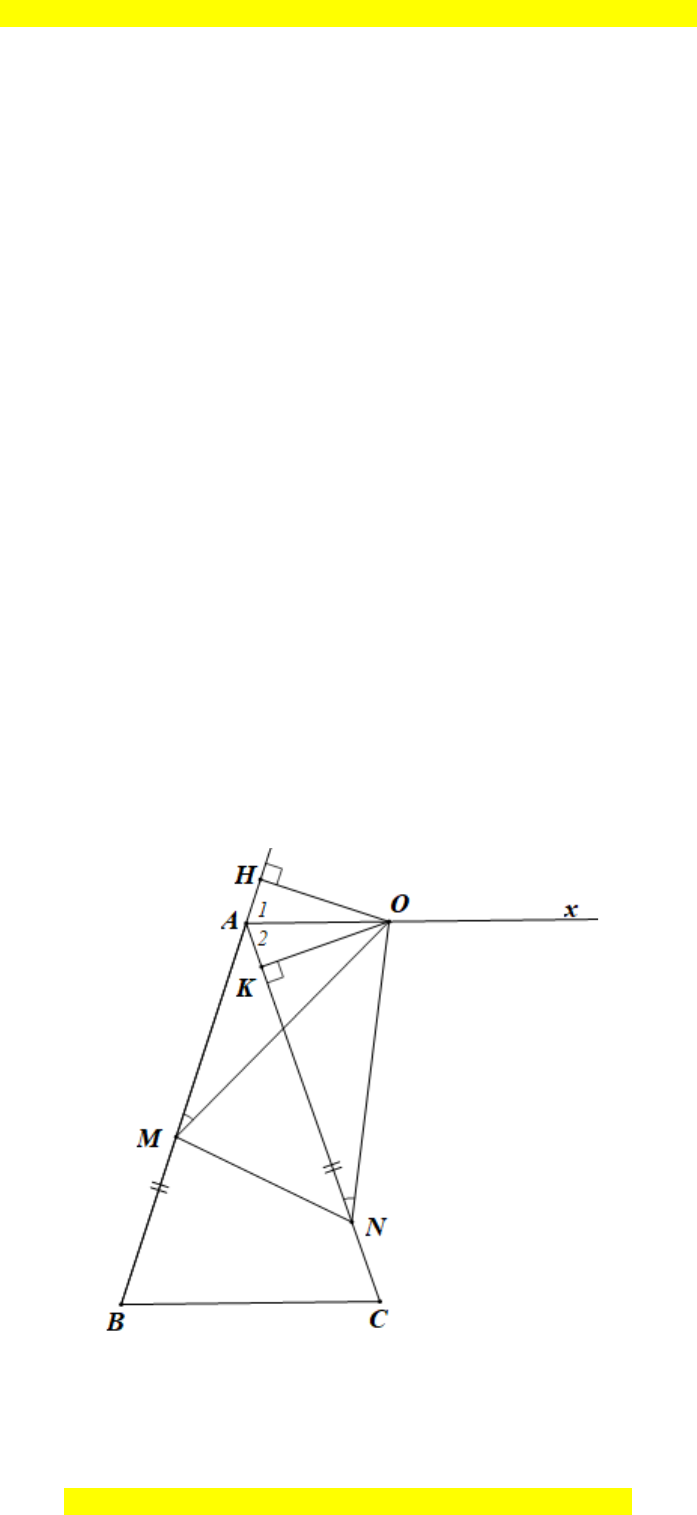
Câu 28. Cho ∆ABC cân tại A. Vẽ tia Ax // BC như hình bên.
Lấy điểm O trên tia Ax, điểm M trên AB và điểm N trên AC sao cho
AMO ANO=
.
Hỏi ∆OMN là tam giác gì?
A. Tam giác cân tại O;
B. Tam giác đều;
C. Tam giác cân tại M;
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
D. Tam giác vuông tại N.
Câu 29. Cho ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối
của tia CA, lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khẳng
định nào sau đây sai?
A. M là trọng tâm của ∆ABD;
B. DM đi qua trung điểm của AB;
C.
1
AM AE
2
=
;
D.
2
BM BC
3
=
.
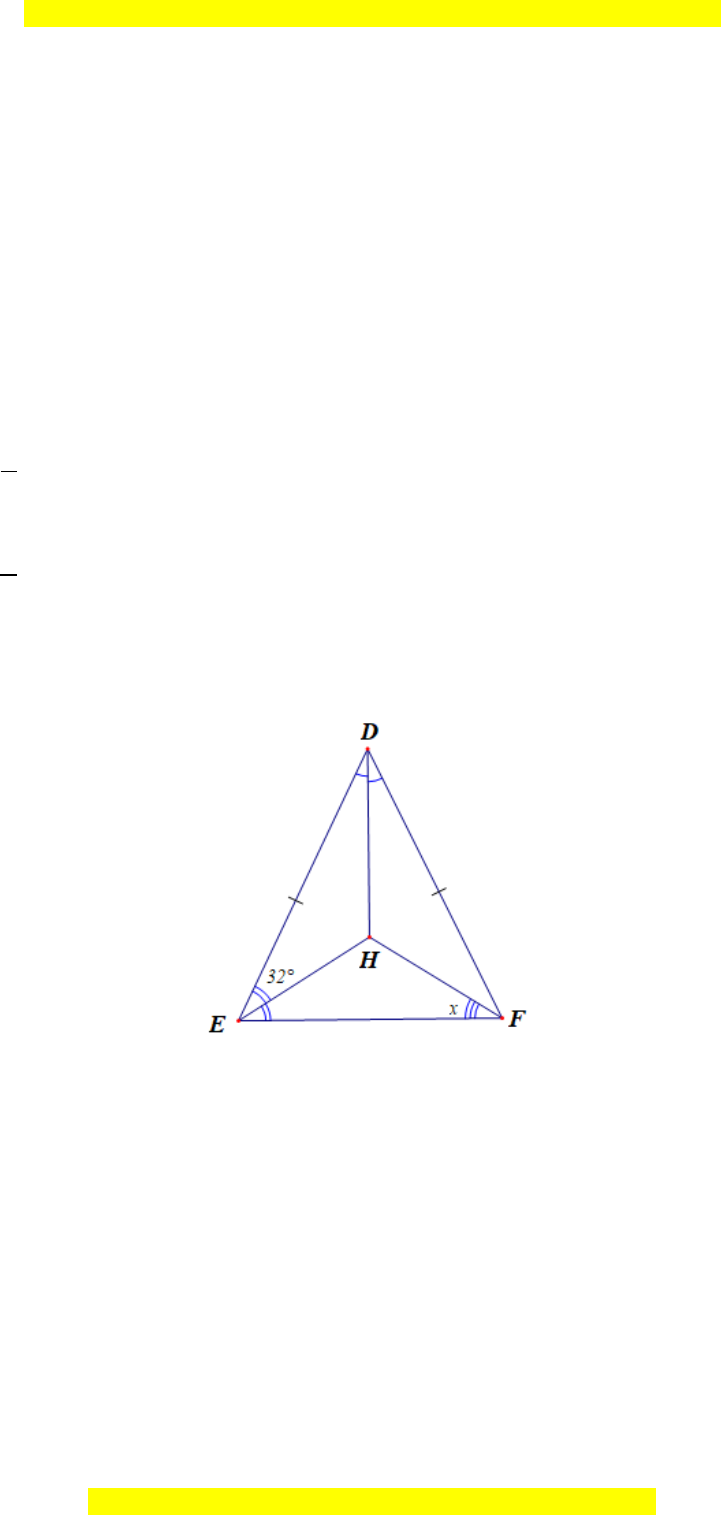
Câu 30. Cho hình vẽ sau:
Biết
DEH 32 .=
Số đo góc x là:
A. x = 26°;
B. x = 32°;
C. x = 64°;
D. x = 128°.
LỜI GIẢI CHI TIẾT
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 1.
Hướng dẫn giải
Đáp án đúng là: C
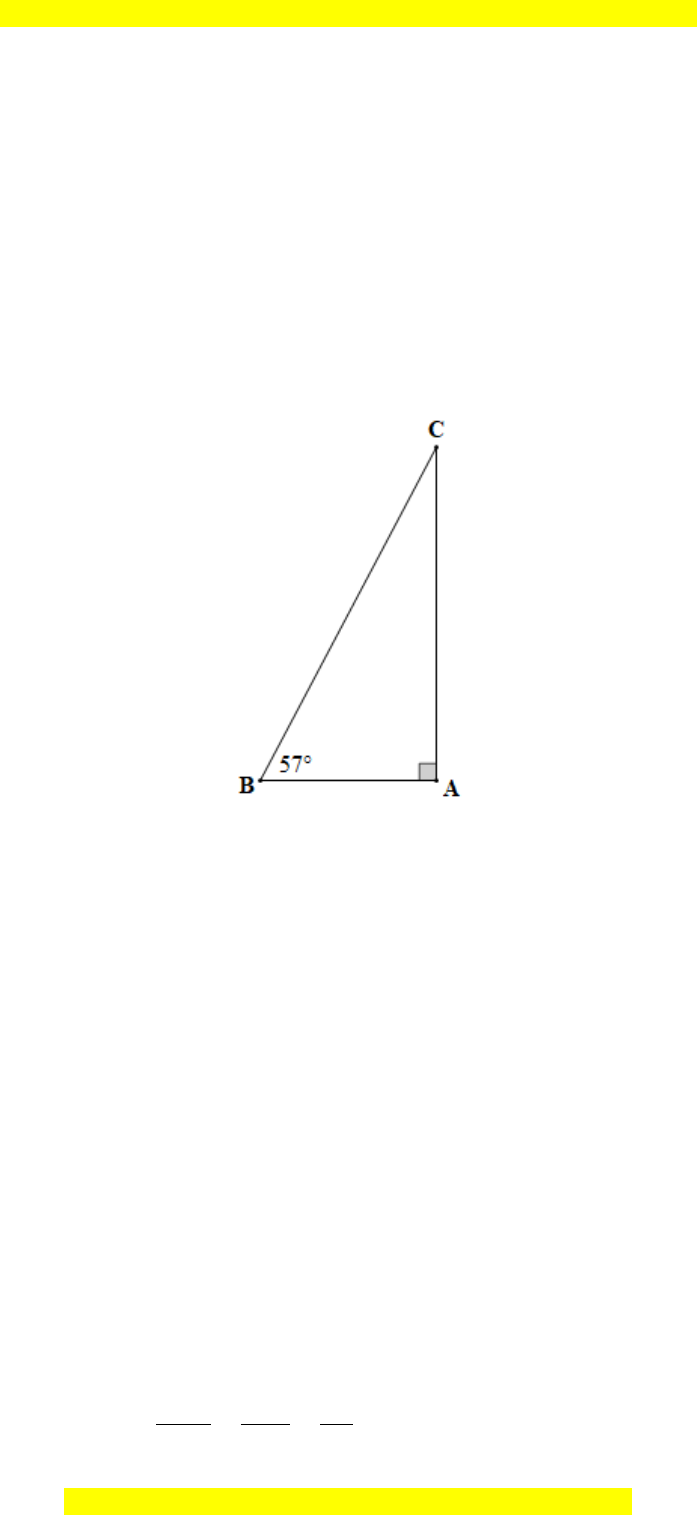
Ta vẽ tam giác ABC vuông tại A có
B 57=
để mô tả hình ảnh chiếc thang dựa vào
tường như đề bài.
Trong tam giác ABC vuông tại A ta có:
B C 90+ =
(trong tam giác vuông, hai góc
nhọn phụ nhau)
Suy ra
C 90 B 90 57 33= − = − =
Vậy độ nghiêng của chiếc thang so với bức tường là 33°.
Câu 2.
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác MNP có
M N P 180+ + =
(tổng ba góc trong một tam giác)
Vì
21M 14N 6P==
nên
21M 14N 6P
42 42 42
==
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
M N P
2 3 7
= =
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
M N P M N P 180
15
2 3 7 2 3 7 12
+ +
= = = = =
++
Suy ra
N 15 .3 45= =
Vậy số đo góc N bằng 45°.
Câu 3.
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC có
A B C 180+ + =
(định lí tổng ba góc trong một tam giác)
Suy ra
A 180 B C= − −
Hay
A 180 72 38 70= − − =
︿
Mà tia AD là tia phân giác của
BAC
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Nên
1
BAD CAD BAC
2
==
(tính chất tia phân giác của một góc)
Suy ra
1
BAD CAD .70 35
2
= = =
Mặt khác:
ADB
là góc ngoài của tam giác ACD tại đỉnh D
Nên
ADB CAD C=+
(tính chất góc ngoài của một tam giác)
Hay
ADB 35 38 73= + =
Vậy số đo góc ADB là 73°.
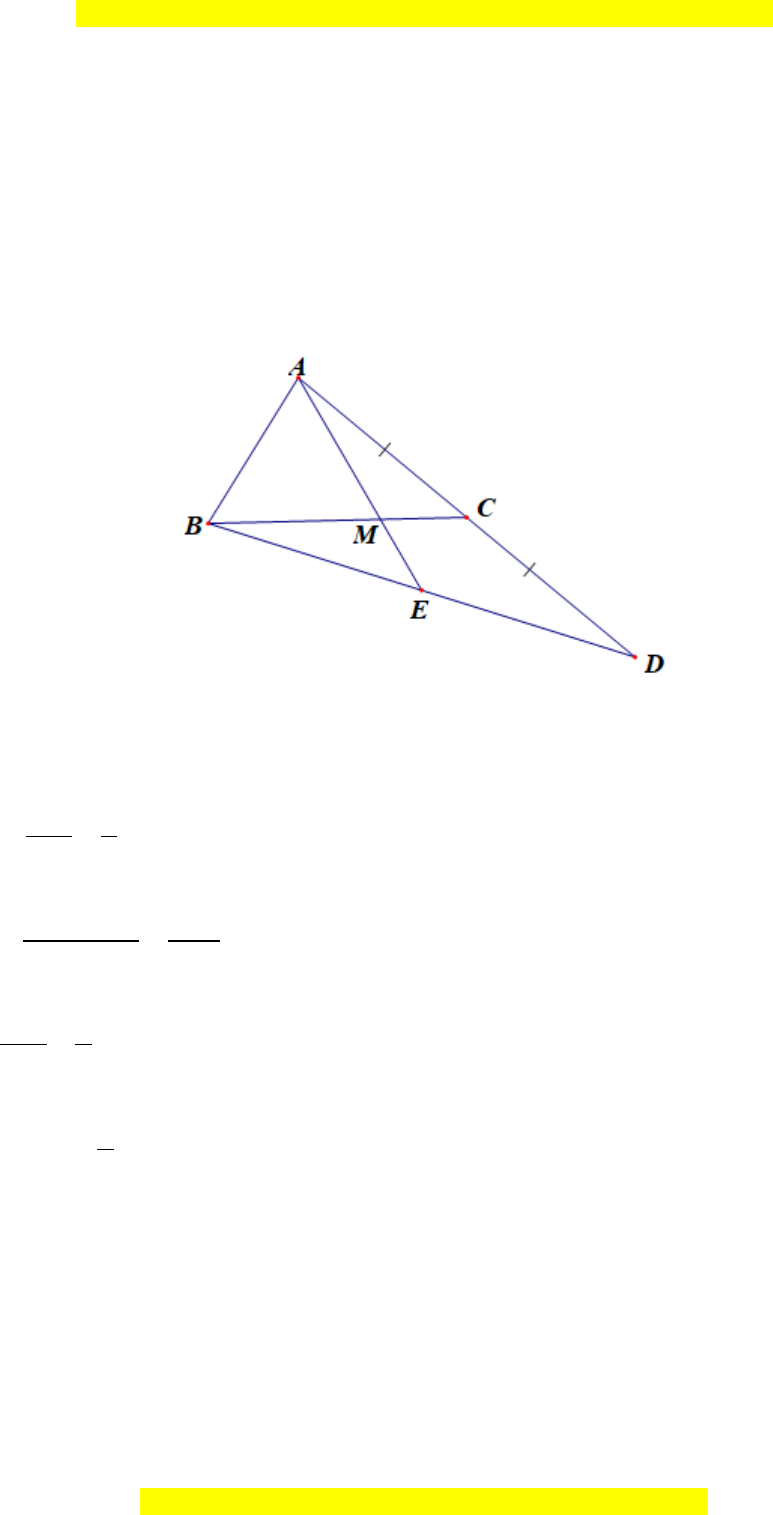
Câu 4.
Hướng dẫn giải
Đáp án đúng là: B
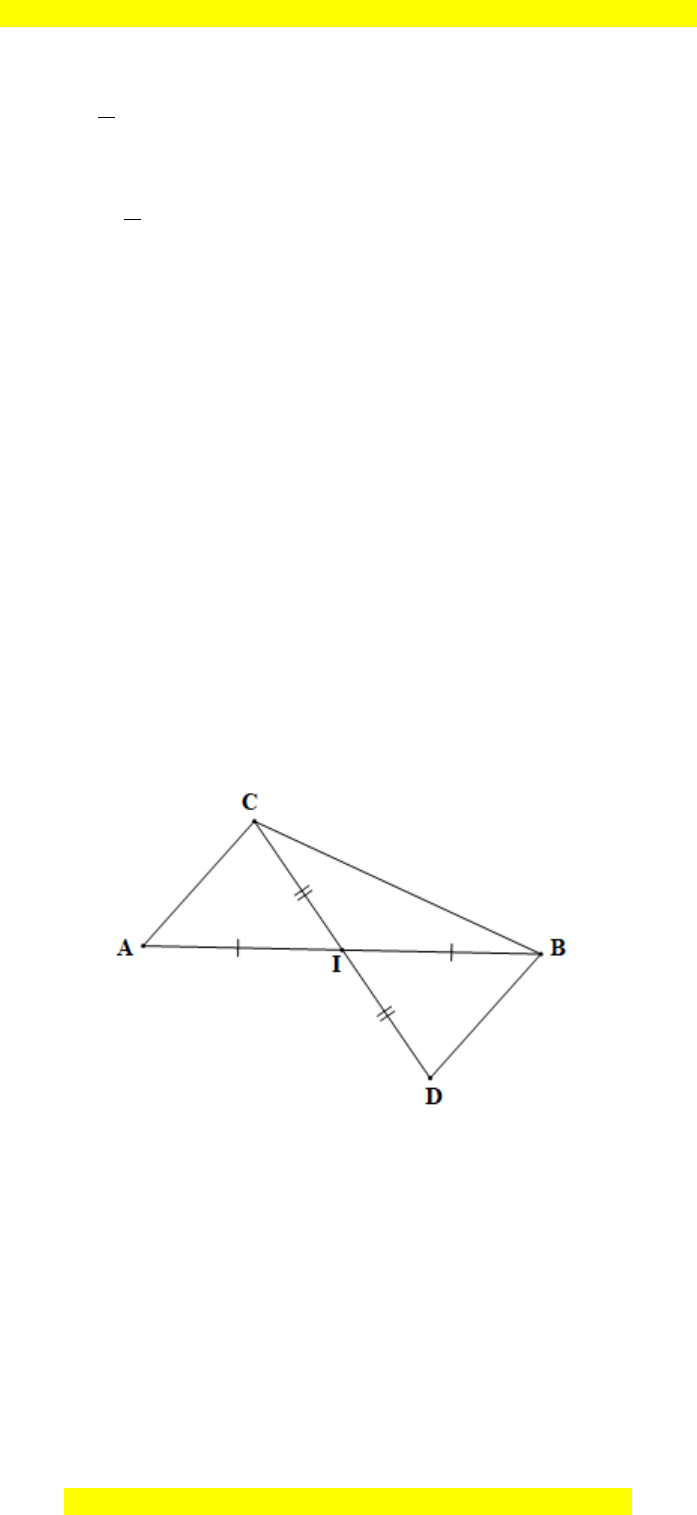
Trên tia đối của tia IC lấy điểm D sao cho ID = IC
Xét ACI và BID có:
AI = BI (vì I là trung điểm của AB);
CI = DI;
AIC BID=
(hai góc đối đỉnh).

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó ACI = BDI (c.g.c)
Suy ra AC = BD (hai cạnh tương ứng)
Xét BCD có: CD < BC + BD (bất đẳng thức trong tam giác)
Hay 2.CI < BC + BD
Do đó 2CI < BC + AC.
Vậy ta chọn đáp án B.
Câu 5.
Hướng dẫn giải
Đáp án đúng là: D
Giả sử tam giác ABC cân có AB = 2 cm và BC = 5 cm.
Áp dụng bất đẳng thức cho tam giác ABC ta có:
BC – AB < AC < BC + AB
Hay 5 – 2 < AC < 5 + 2
Suy ra 3 < AC < 7 (*)
Vì tam giác ABC là tam giác cân (giả thiết)
Mà AB = 2 cm và BC = 5 cm nên không thể cân tại B.
Do đó có hai trường hợp có thể xảy ra:
• Trường hợp 1: ABC cân tại A.
Suy ra AB = AC.
Mà AB = 2 cm nên AC = 2 cm (không thỏa mãn điều kiện (*))
Nên AB = 2 cm hoặc AB = 5 cm (2)
• Trường hợp 2: ABC cân tại C.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Suy ra CA = CB.
Mà BC = 5 cm nên AC = 5 cm (thỏa mãn điều kiện (*))
Vậy AC = 5 cm.
Khi đó chu vi tam giác ABC là:
AB + AC + BC = 2 + 5 + 5 = 12 (cm).
Ta chọn phương án D.
Câu 5
Đáp án đúng là: A
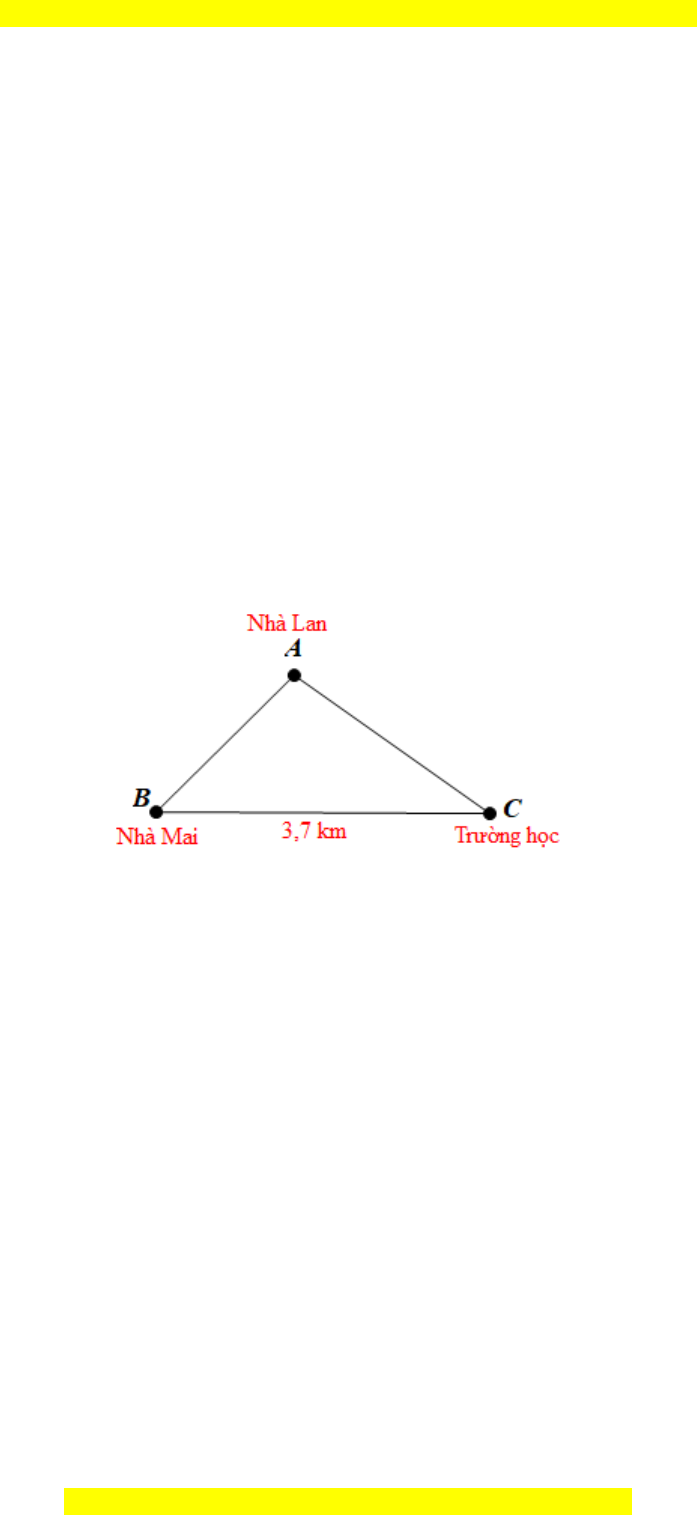
Đặt ba điểm tại ba vị trí như hình vẽ trên.
Theo bất đẳng thức ta có:
AB + AC > BC
Nên AB + AC > 3,7 cm.
Do đó tổng quãng đường từ nhà Mai đến nhà Lan rồi từ nhà Lan tới trường học phải
lớn hơn 3,7 km.
Vậy nên bạn Mai đã nói sai.
Ta chọn phương án A.
Câu 6.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC ta có:
A B C 180+ + =
(định lí tổng ba góc trong một tam giác)
Suy ra
A 180 B C= − −
Hay
A 180 80 40 60= − − =
Xét tam giác MNP ta có:
M N P 180+ + =
(định lí tổng ba góc trong một tam giác)
Suy ra
P 180 N M= − −
Hay
P 180 80 60 40= − − =
Khi đó: tam giác ABC và tam giác MNP có:
+) AB = NM, BC = NP, AC = MP;
+)
( ) ( ) ( )
A M 60 ,B N 80 ,C P 40= = = = = =
Do đó hai tam giác ABC và MNP bằng nhau và được kí hiệu là ABC = MNP.
Vậy ta chọn phương án A.
Câu 7.
Hướng dẫn giải
Đáp án đúng là: A
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, AC = MP (giả thiết)
Suy ra ABC = MNP (c.c.c)
Do đó
AM=
,
BN=
,
CP=
(các cặp góc tương ứng)
Mà
A 65=
,
N 70=
nên
M 65 ,B 70= =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Xét tam giác ABC có:
A B C 180+ + =
(tổng ba góc trong một tam giác)
Suy ra
C 180 B A= − −
Hay
C 180 70 65 45= − − =
Vậy số đo góc C và góc M lần lượt là: 45° và 65°.
Câu 8.
Hướng dẫn giải
Đáp án đúng là: A
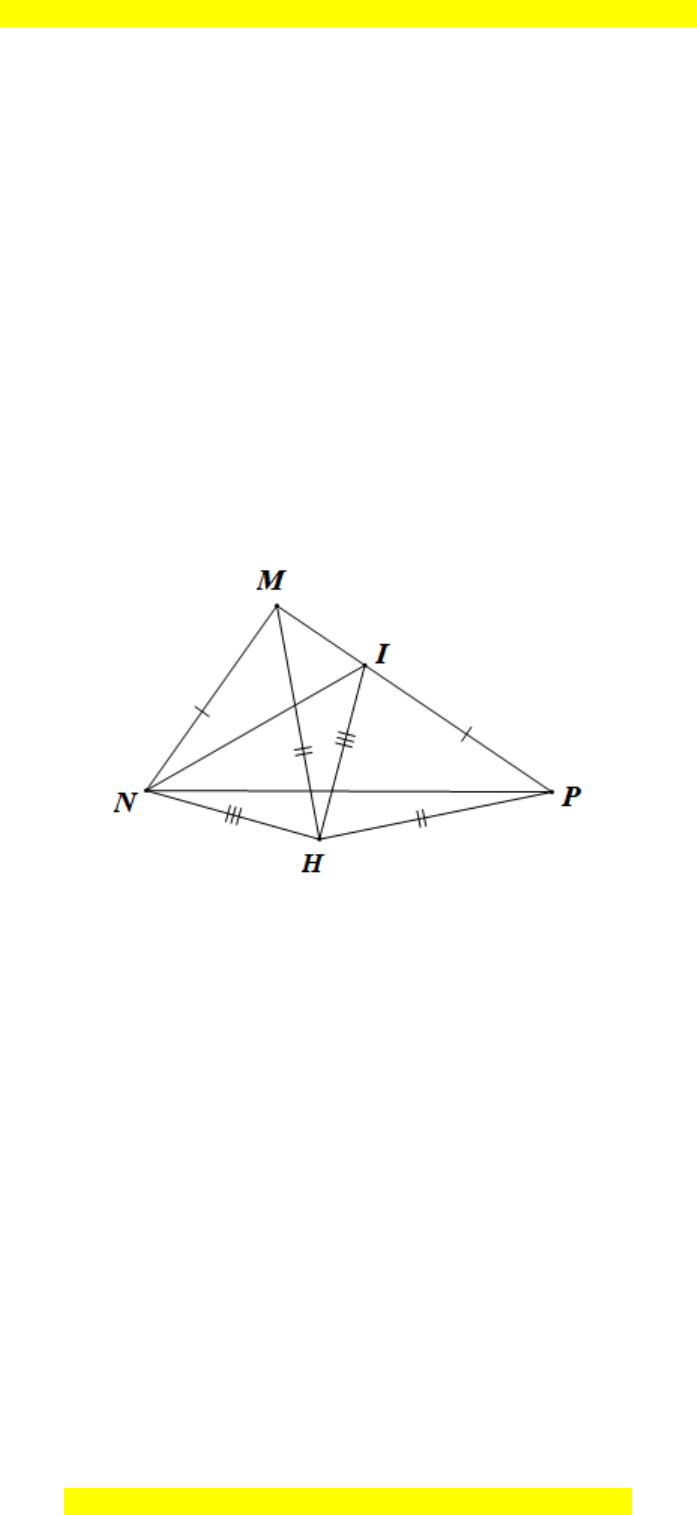
Xét MNH và HIP ta có:
HM = HP (giả thiết);
HN = HI (giả thiết);
MN = PI (giả thiết).
Do đó MNH = PIH (c.c.c)
Suy ra
MNH PIH,MHN PHI==
(các cặp góc tương ứng)
Vậy ta chọn phương án A.
Câu 9.
Hướng dẫn giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
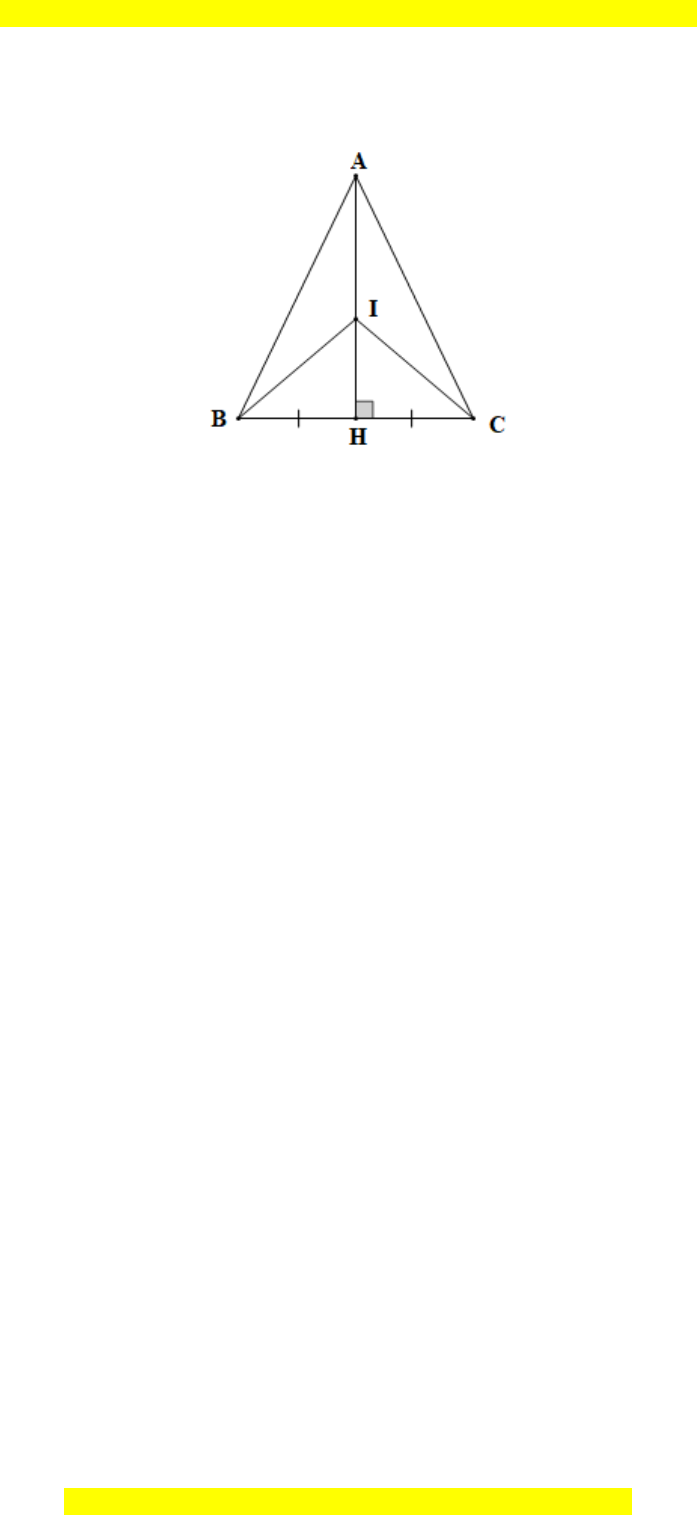
Đáp án đúng là: D
Vì A nằm trên đường thẳng vuông góc với CB tại H nên ta có:
AHB AHC 90= =
Vì I nằm trên đường thẳng vuông góc với CB tại H nên ta có:
IHB IHC 90= =
+) Xét ABH và ACH có:
AHB CHA 90= =
(chứng minh trên),
AH là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ABH = ACH (hai cạnh góc vuông)
Do đó đáp án A đúng
Vì ABH = ACH (chứng minh trên)
Suy ra AB = AC (hai cạnh tương ứng) và
BAH CAH=
(hai góc tương ứng)
+) Xét tam giác HCI và tam giác HBI có:
IHB IHC 90= =
(chứng minh trên),
HI là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ICH = IBH (hai cạnh góc vuông)
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó đáp án B đúng
+) Xét tam giác BAI và tam giác CAI có:
AB = AC (chứng minh trên),
BAI CAI=
(do
BAH CAH=
),
AI là cạnh chung
Suy ra BAI = CAI (c.g.c)
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Câu 10.
Hướng dẫn giải
Đáp án đúng là: B
Vì ABCD là hình vuông (giả thiết) nên AD = CD (tính chất hình vuông)
Do đó AE + ED = CF + FD
Mà AE = FD (giả thiết) nên ED = CF.
Xét FED và GFC có:
FD = CG (giả thiết),
DC=
(
90 ,=
tính chất hình vuông),

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
ED = CF (chứng minh trên)
Do đó FED = GFC (hai cạnh góc vuông)
Suy ra
FED CFG=
(hai góc tương ứng)
Mà
FED DFE 90+ =
(trong tam giác FDE vuông tại D, hai góc nhọn phụ nhau)
Do đó
GFC DFE 90+ =
Mặt khác
GFC DFE GFE 180+ + =
Suy ra
( )
GFE 180 GFC DFE 180 90 90= − + = − =
Vậy
GFE 90 .=
Câu 11.
D. 4,5 cm.
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
•
AHC CHK 180+ =
(hai góc kề bù);
•
BKD DKH 180+ =
(hai góc kề bù)
Mà
HKD CHK=
(giả thiết) nên
AHC DBK=
Vì AHC vuông tại A nên
AHC ACH 90+ =
(trong tam giác vuông, hai góc nhọn phụ
nhau)
Vì BKD vuông tại B nên
BKD BDK 90+ =
(trong tam giác vuông, hai góc nhọn
phụ nhau)
Mà
AHC BKD=
(chứng minh trên) nên
HCA BDK=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Xét AHC và BKD có:
AB=
(= 90°)
HCA BDK=
(chứng minh trên),
AC = BD (giả thiết),
Do đó AHC = BKD (cạnh góc vuông – góc nhọn kề)
Suy ra CH = DK (hai cạnh tương ứng)
Mà CH = 3,5 cm nên DK = 3,5 cm.
Câu 12.
Hướng dẫn giải
Đáp án đúng là: D
• Vì AB // HK (giả thiết) nên
BAC ACH=
(hai góc so le trong)
Vì BC // IH (giả thiết) nên
BCA CAH=
(hai góc so le trong)
• Xét ABC và CHA có:
BAC ACH=
(chứng minh trên),
AC là cạnh chung,
BCA CAH=
(chứng minh trên)

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó ABC = CHA (g.c.g)
Suy ra BC = AH (hai cạnh tương ứng)
Mà AH = AI (do A là trung điểm của IH)
Do đó BC = AI nên đáp án C là đúng.
• Vì CH // AB (giả thiết) nên
BAI CHA=
(hai góc đồng vị)
Vì IH // CB (giả thiết) nên
KCB CHA=
và
KBC BIA=
(các cặp góc đồng vị)
Do đó
BAI CHA KCB==
Xét ABI và CKB có:
BAI KCB=
(chứng minh trên),
AI = BC (chứng minh trên),
KBC BIA=
(chứng minh trên),
Do đó ABI = CKB (g.c.g) nên đáp án B là đúng
Suy ra AB = KC (hai cạnh tương ứng)
Mà ABC = CHA (chứng minh trên)
Nên AB = CH (hai cạnh tương ứng)
Do đó CH = CK (= AB) nên đáp án A là đúng
Vậy ta chọn đáp án D.
Câu 13.
Hướng dẫn giải
Đáp án đúng là: D

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta xét từng đáp án:
Đáp án A:
Xét ∆ADH và ∆ADE, có:
AH = AE (giả thiết).
HAD DAE=
(do AD là phân giác của
HAC
).
AD là cạnh chung.
Do đó ∆ADH = ∆ADE (c.g.c)
Suy ra đáp án A đúng.
Đáp án B:
∆ADH = ∆ADE (chứng minh trên).
Suy ra
AHD AED=
(cặp góc tương ứng).
Mà
AHD 90=
(do AH ⊥ HD).
Do đó
AED 90=
.
Khi đó ta có DE ⊥ AE hay DE ⊥ AC.
Do đó đáp án B đúng.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đáp án C:
Ta có AH = AE (giả thiết) và HF = EC (giả thiết).
Suy ra AH + HF = AE + EC.
Do đó AF = AC.
Khi đó ta có ∆ACF cân tại A (1).
Vì ∆AHC vuông tại H nên
HAC HCA 90+ =
.
Do đó
HAC 90 HCA 90 30 60= − = − =
(2).
Từ (1), (2), ta suy ra ∆ACF là tam giác đều.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Câu 14.
Hướng dẫn giải
Đáp án đúng là: A
Trên hình vẽ, hai đường trung tuyến BN và CP cắt nhau tại G
Nên G là trọng tâm tam giác ABC
Do đó
2
AG AM
3
=
(tính chất trọng tâm)
Suy ra
1
GM AM
3
=
Mà AM = 3 cm
Nên GM = 1 cm.
Vậy ta chọn phương án A.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 15.
Hướng dẫn giải
Đáp án đúng là:
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung,
BAD CAD=
(do AD là tia phân giác của
BAC
),
AB = AC (do ∆ABC cân tại A).
Do đó ∆ADB = ∆ADC (c.c.c).
Suy ra đáp án C đúng.
Ta có ∆ADB = ∆ADC (chứng minh trên).
Suy ra BD = CD và
ADB ADC=
(cặp cạnh và cặp góc tương ứng).
Vì BD = CD nên D là trung điểm BC.
Do đó đáp án A đúng.
Ta có
ADB ADC 180+ =
(hai góc kề bù).
Suy ra
ADB ADC 180 :2 90= = =
.
Do đó AD ⊥ BC.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
∆ABD vuông tại D:
ABD BAD 90+ =
.
Mà
BAD CAD=
(AD là phân giác của
BAC
).
Suy ra
ABC CAD 90+ =
.
Do đó đáp án B đúng.
Ta có
ABC CAD 90+ =
.
Suy ra
ABC 90
.
Do đó
ABC ADC 90 90 180+ + =
.
Do đó đáp án D sai.
Vậy ta chọn đáp án D.
Câu 16.
Hướng dẫn giải
Đáp án đúng là: B
Điểm cách đều ba đỉnh của tam giác là giao điểm của ba đường trung trực của tam
giác đó.
Trọng tâm là giao điểm của ba đường trung tuyến của một tam giác.
Điểm cách đều ba cạnh của tam giác là giao điểm của ba đường phân giác của tam
giác đó.
Trực tâm là giao điểm của ba đường cao của một tam giác.
Vậy ta chọn phương án B.
Câu 17
Hướng dẫn giải
Đáp án đúng là: D

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
Do đó ta chọn phương án D.
Câu 18.
Hướng dẫn giải
Đáp án đúng là: D
Ta xét từng phát biểu:
Ba đường trung tuyến của một tam giác đồng quy tại một điểm, điểm đó là trọng tâm
của tam giác đó.
Do đó phát biểu (I) đúng.
Ba đường phân giác của một tam giác đồng quy tại một điểm, điểm đó cách đều ba
cạnh của tam giác đó.
Do đó phát biểu (II) đúng.
Ba đường trung trực của một tam giác đồng quy tại một điểm, điểm đó cách đều ba
đỉnh của tam giác đó.
Do đó phát biểu (III) đúng.
Ba đường cao của một tam giác đồng quy tại một điểm, điểm đó được gọi là trực tâm
của tam giác đó.
Do đó phát biểu (IV) đúng.
Vậy có 4 phát biểu đúng, ta chọn phương án D.
Câu 19.
Hướng dẫn giải
Đáp án đúng là: A

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
Để xác định trực tâm của một tam giác, ta cần xác định giao điểm của ít nhất hai
đường cao của tam giác đó.
Vì ∆ABC vuông tại A nên ta có AB ⊥ AC tại A.
Suy ra ∆ABC có hai đường cao là AB và AC.
Hai đường cao này cắt nhau tại A.
Do đó A là trực tâm của ∆ABC.
Vậy ta chọn phương án A.
Câu 20.
Hướng dẫn giải
Đáp án đúng là: C
• Vì AB là đường trung trực của đoạn thẳng PQ và AB cắt PQ tại I.
Ta suy ra I là trung điểm của PQ.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó đáp án A đúng.
• Vì A nằm trên đường trung trực của đoạn thẳng PQ.
Nên A cách đều P, Q.
Suy ra AQ = AP = 6 cm.
Mà BQ = 8 cm.
Do đó đáp án B đúng.
Vậy ta chọn đáp án C.
Câu 21
Hướng dẫn giải
Đáp án đúng là: B
Vì M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB (1).
Xét ∆CMB, có: MC + MB > BC (bất đẳng thức tam giác) (2).
Từ (1), (2), ta suy ra MC + MA > BC.
Vậy ta chọn phương án B.
Câu 22.
Hướng dẫn giải
Đáp án đúng là: C

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
• Xét ∆BOD và ∆COE, có:
BDO CEO 90= =
,
OB = OC (do O là trung điểm của BC),
BOD COE=
(hai góc đối đỉnh),
Do đó ∆BOD = ∆COE (cạnh huyền – góc nhọn).
Suy ra OD = OE (cặp cạnh tương ứng).
• ∆AOB có
B 90
(giả thiết).
Ta suy ra OA là cạnh lớn nhất trong ba cạnh AO, OB, AB của ∆AOB.
Do đó AB < OA.
Khi đó ta có AB < AD + OD (1) và AB < AE – OE (2).
Lấy (1) + (2) vế theo vế, ta được:
2AB < AD + OD + AE – OE.
Suy ra 2AB < AD + AE + OD – OD (vì OD = OE (chứng minh trên)).
Do đó 2AB < AD + AE.
Vì vậy
AD AE
AB
2
+
.
E
D
O
A
B
C
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy ta chọn đáp án C.
Câu 23.
Hướng dẫn giải
Đáp án đúng là: D
• Xét ∆ABC và ∆ADE, có:
AB = AD (giả thiết),
BAC DAE=
(hai góc đối đỉnh),
AC = AE (giả thiết).
Do đó ∆ABC = ∆ADE (c.g.c)
Suy ra BC = DE (cặp cạnh tương ứng).
Vì vậy đáp án A đúng.
• Xét ∆ABD có DA ⊥ AB (do ∆ABC vuông tại A).
Suy ra
BAD 90=
.
Do đó ∆ABD vuông tại A.
Lại có AB = AD (giả thiết).
Suy ra ∆ABD vuông cân tại A.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó đáp án B đúng.
• Chứng minh tương tự, ta được ∆ACE vuông cân tại A.
Suy ra
BDA ACE 45= =
.
Mà hai góc này ở vị trí so le trong.
Do đó BD // CE.
Vì vậy đáp án C đúng.
Vậy ta chọn phương án D.
Câu 24.
Hướng dẫn giải
Đáp án đúng là: D
• Ta có:
+)
ACN ABM=
(cùng phụ với
BAC
);
+)
PBA ABM 180+ =
(hai góc kề bù);
+)
ACQ ACN 180+ =
(hai góc kề bù).
Do đó
PBA ACQ=
.
Vì vậy đáp án C đúng.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
• Xét ∆BAP và ∆CQA, có:
BA = CQ (giả thiết),
PBA ACQ=
(chứng minh trên),
BP = AC (giả thiết)
Do đó ∆BAP = ∆CQA (c.g.c)
Vì vậy đáp án B đúng.
• Ta có ∆BAP = ∆CQA (chứng minh trên).
Suy ra AP = AQ và
CAQ BPA=
(cặp cạnh và cặp góc tương ứng).
∆APQ có
PAQ PAC CAQ PAC BPA= + = +
PAM APM 90= + =
(do ∆PAM vuông tại M).
Suy ra ∆APQ vuông tại A.
Mà AP = AQ (chứng minh trên).
Do đó ∆APQ vuông cân tại A.
Vì vậy đáp án A đúng.
Vậy ta chọn đáp án D.
Câu 25.
Hướng dẫn giải
Đáp án đúng là: D

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
• Xét ∆ABE và ∆ACD, có:
BAE CAD 90= =
,
AE = AD (giả thiết),
AB = AC (do ∆ABC vuông cân tại A).
Do đó ∆ABE = ∆ACD (hai cạnh góc vuông)
Suy ra
ACD ABE=
(cặp góc tương ứng).
Vì vậy đáp án A đúng.
• Gọi F là giao điểm của CD và BE.
Ta có
FDB ADC=
(hai góc đối đỉnh).
Xét ∆ACD vuông tại A có:
ADC ACD 90+ =
(trong tam giác vuông, hai góc nhọn
phụ nhau)
Suy ra
FDB DBF 90+ =
.
∆DBF có:
BFD FDB DBF 180+ + =
(định lí tổng ba góc của một tam giác)
Suy ra
( )
BFD 180 FDB DBF 180 90 90= − + = − =
.
Do đó BF ⊥ FD hay BE ⊥ CD.
Do đó đáp án B đúng.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
• Xét ∆BCE có BA, CD là hai đường cao.
Mà BA cắt CD tại D.
Suy ra D là trực tâm của ∆BCE.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Câu 26.
Hướng dẫn giải
Đáp án đúng là: A
• Gọi M, N lần lượt là trung điểm BE, AC.
Vì IM là đường trung trực của đoạn thẳng BE nên IB = IE.
Vì IN là đường trung trực của đoạn thẳng AC nên IA = IC.
Do đó đáp án D đúng.
• Xét ∆AIB và ∆CIE, có:
IA = IC (chứng minh trên),
AB = CE (giả thiết),
IB = IE (chứng minh trên)
Do đó ∆AIB = ∆CIE (cạnh – cạnh – cạnh).
Vì vậy đáp án A sai do chưa đúng kí hiệu bằng nhau của hai tam giác.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
• Ta có ∆AIB = ∆CIE (chứng minh trên).
Suy ra
IAB ICA=
(cặp góc tương ứng).
Mà
IAC ICA=
(do ∆IAC cân tại I).
Do đó
IAB IAC=
.
Vì vậy đáp án C đúng.
• Ta có
IAB IAC=
(chứng minh trên).
Suy ra AI là tia phân giác của
BAC
.
Hay AI là đường phân giác của ∆ABC.
Do đó đáp án B đúng.
Vậy ta chọn đáp án C.
Câu 27.
Hướng dẫn giải
Đáp án đúng là: D
+) ∆BEC có EM là đường trung trực của cạnh BC (giả thiết).
Ta suy ra EB = EC.
Do đó ∆BEC cân tại E.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vì vậy đáp án A đúng.
+) Vì ∆BEC cân tại E nên
ECB EBC 30= =
.
Ta có:
•
ABE ABC EBC 75 30 45= − = − =
;
•
ACE ACB ECB 45 30 15= − = − =
.
Suy ra
ABE ACE 45 15 60+ = + =
(1).
∆ABC có:
BAC ABC ACB 180+ + =
(định lí tổng ba góc trong một tam giác)
Suy ra
BAC 180 ABC ACB 180 75 45 60= − − = − − =
(2).
Từ (1), (2), ta suy ra
BAC ABE ACE=+
.
Do đó đáp án B đúng.
+) Xét phương án C
• Nếu
AEB 90
thì:
∆ABE có
1
A ABE AEB 180+ + =
(định lí tổng ba góc trong một tam giác)
Suy ra
1
A 180 ABE AEB 180 45 90 45= − − − − =
.
Do đó
1
A ABE
(3).
Suy ra BE < AE (quan hệ giữa cạnh và góc đối diện)
Vì vậy EC < AE (∆BCE cân tại E).
Suy ra
2
A ACE
(4).
Từ (3), (4), ta suy ra
12
A A ABE ACE 60+ + =
.
Điều này vô lý vì
12
A A BAC 60+ = =
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó ta loại trường hợp
AEB 90
.
• Nếu
AEB 90
thì:
Ta lập luận tương tự, ta được AE < EC và
12
A A 45 15 60+ + =
.
Điều này vô lý vì
12
A A BAC 60+ = =
.
Do đó ta loại trường hợp
AEB 90
.
Vì vậy
AEB 90=
.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Câu 28.
Hướng dẫn giải
Đáp án đúng là: A
• Ta có Ax // BC nên
1
AB=
(cặp góc đồng vị) và
2
AC=
(cặp góc so le trong).

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Mà
BC=
(do ∆ABC cân tại A).
Suy ra
12
AA=
.
• Kẻ OH ⊥ AB và OK ⊥ AC.
Xét ∆AHO và ∆AKO, có:
AHO AKO 90= =
,
AO là cạnh chung,
12
AA=
(chứng minh trên),
Do đó ∆AHO = ∆AKO (cạnh huyền – góc nhọn).
Suy ra OH = OK (cặp cạnh tương ứng).
• ∆HOM vuông tại H:
HMO MOH 90+ =
(1).
• ∆KON vuông tại K:
KNO NOK 90+ =
(2).
Ta có
HMO KNO=
(giả thiết) (3).
Từ (1), (2), (3), ta suy ra
MOH NOK=
.
• Xét ∆HOM và ∆KON, có:
OHM OKN 90= =
,
OH = OK (chứng minh trên),
MOH NOK=
(chứng minh trên),
Do đó ∆HOM = ∆KON (cạnh góc vuông – góc nhọn kề)
Suy ra OM = ON (cặp cạnh tương ứng).
Vì vậy ∆OMN cân tại O.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy ta chọn đáp án A.
Câu 29.
Hướng dẫn giải
Đáp án đúng là: C
• Ta có BM = 2MC.
Suy ra
BM 2
MC 1
=
Do đó
BM 2
MC BM 1 2
=
++
Hay
BM 2
BC 3
=
Suy ra
2
BM BC
3
=
(1).
Do đó đáp án D đúng.
• Vì ∆ABD có AC = CD nên C là trung điểm AD.
Do đó BC là đường trung tuyến của ∆ABD (2).
Từ (1), (2), ta suy ra M là trọng tâm của ∆ABD.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó đáp án A đúng.
• Vì M là trọng tâm của ∆ABD nên DM đi qua trung điểm của cạnh AB.
Do đó đáp án B đúng.
• Vì M là trọng tâm của ∆ABD nên
21
AM AE AE
32
=
.
Do đó đáp án C sai.
Vậy ta chọn đáp án C.
Câu 30.
Hướng dẫn giải
Đáp án đúng là: B
• Ta có DE = DF nên ∆DEF cân tại D.
Suy ra
DFE DEF=
(tính chất tam giác cân)
Mà
DEH HEF 32= =
Do đó EH là tia phân giác của
DEF
Suy ra
DEF 2DEH 2.32 64= = =
.
Nên
DFE 64=
• ∆DEF có hai đường phân giác DH và EH cắt nhau tại H.
Ta suy ra FH là đường phân giác thứ ba của ∆DEF.
Do đó
11
x HFE DFE .64 32
22
= = = =
.
Vậy ta chọn đáp án B.

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85