Bài 8. Đường vuông góc và đường xiên
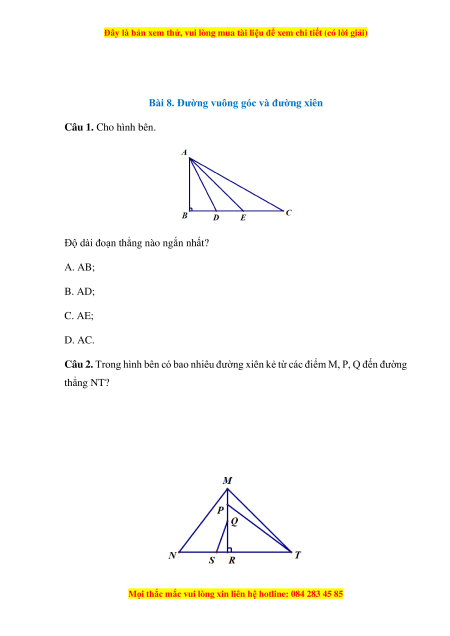
Câu 1. Cho hình bên.
Độ dài đoạn thẳng nào ngắn nhất? A. AB; B. AD; C. AE; D. AC.
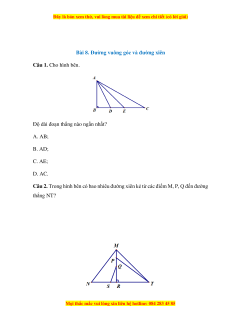
Câu 2. Trong hình bên có bao nhiêu đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT?
A. 2; B. 3; C. 4; D. 5.
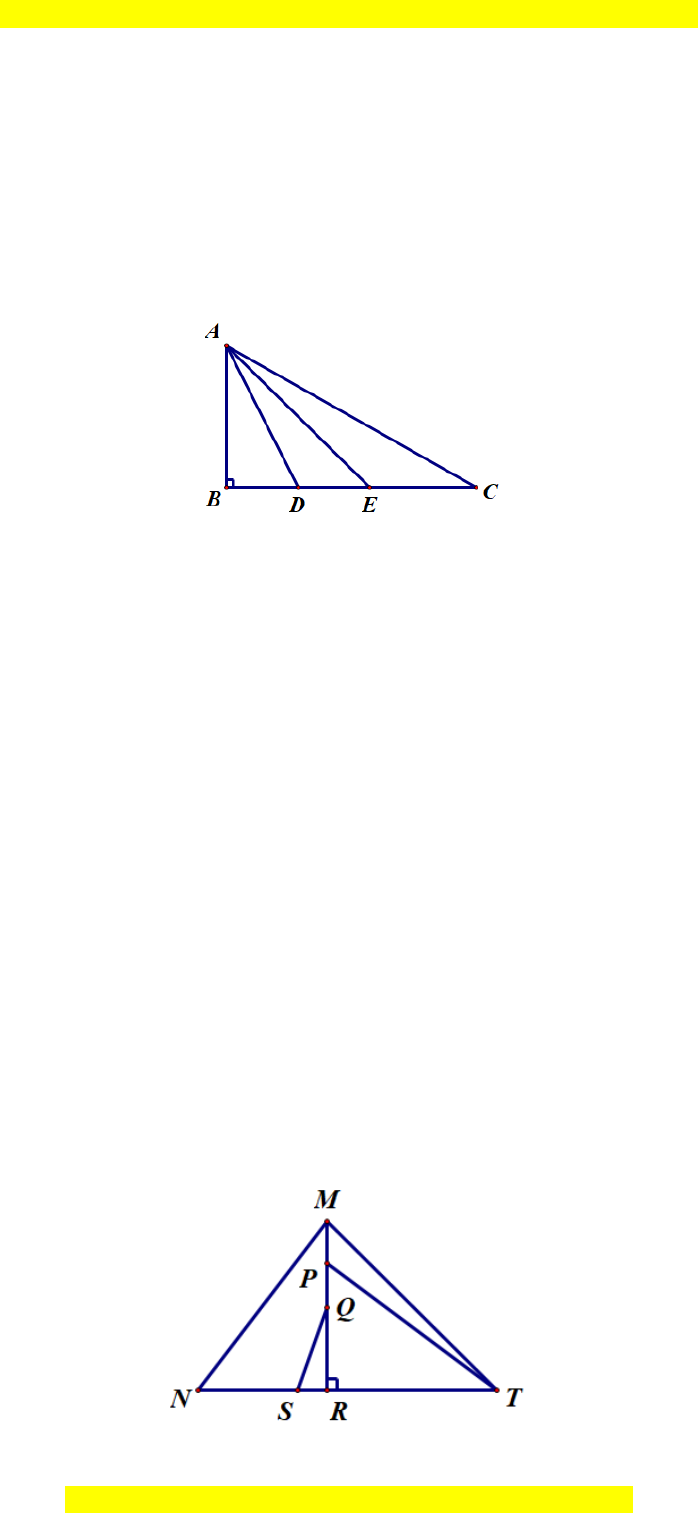
Câu 3. Cho ∆ABC có AD là đường cao như hình bên.
Trong ba cạnh AB, AD, AC, cạnh nào ngắn nhất? A. AD; B. AB; C. AC;
D. Không thể so sánh được.
Câu 4. Cho ∆ABC vuông tại A. Kẻ AH ⊥ BC (H ∈ BC). Có bao nhiêu đường
vuông góc kẻ từ các điểm A, B, C đến các đường thẳng có trong hình bên? A. 3; B. 4;
C. 5; D. 7.
Câu 5. Cho ∆ABC vuông tại B. Trên đường thẳng BC lấy điểm I, J, K sao cho AI
< AJ < AK. Hỏi B là hình chiếu của các điểm nào lên đường thẳng AB? A. C, J, A, K; B. A, C, K, J; C. I, J, C, A; D. I, J, C, K.
Câu 6. Cho ∆ABC (AB < AC), đường cao AH (H ∈ BC). Lấy điểm K bất kì thuộc
AH (K ≠ H). Trong các đoạn thẳng AB, AC, AH, BK, CK, KH, đoạn thẳng nào ngắn nhất? A. AH; B. KH; C. BK; D. CK.
Câu 7. Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường
vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC.
So sánh BC và tổng DH + DK. A. DH + DK > BC; B. DH + DK < BC; C. DH + DK = BC;
D. Không thể so sánh được.
Câu 8. Cho ∆ABC có ABC = 30 , ACB = 70 . Gọi H là chân đường vuông góc
kẻ từ B. Khẳng định nào sau đây đúng? A. HA > AC; B. HA < AC; C. HA = AC; D. BAC = 70 .
Câu 9. Cho ∆ABC. Vẽ AD ⊥ BC, BE ⊥ AC, CF ⊥ AB (D ∈ BC, E ∈ AC, F ∈
AB). So sánh AD + BE + CF và chu vi C của ∆ABC. A. AD + BE + CF = C; B. AD + BE + CF < C; C. AD + BE + CF > C;
D. Không thể so sánh được.
Câu 10. Cho ∆MNP vuông tại M. Vẽ MH ⊥ NP tại H. Trên cạnh NP lấy điểm E
sao cho NE = MN. Trên cạnh MP lấy điểm F sao cho MF = MH. Khoảng cách từ
E đến đường thẳng MP là đoạn thẳng: A. EM; B. EF; C. EP; D. EN.
Câu 11. Cho ∆ABC vuông tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy
điểm F. So sánh độ dài các cạnh EA và BF. A. EA = BF; B. EA < BF;
Trắc nghiệm Đường vuông góc và đường xiên Toán 7 Cánh diều
131
66 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Bộ câu hỏi trắc nghiệm Toán 7 Cánh diều học kì 2 mới nhất nhằm giúp Giáo viên có thêm tài liệu tham khảo Trắc nghiệm Toán lớp 7.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(131 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 26 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án150.000 ₫ - 200.000 ₫ 44.7 K 22.4 K lượt tải
-
Bộ 20 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án150.000 ₫ 25.2 K 12.6 K lượt tải
-
Bộ Trắc nghiệm Toán 7 Kết nối tri thức (cả năm) có đáp án200.000 ₫ 16.2 K 8.1 K lượt tải
-
Bài giảng Powerpoint Toán 7 Kết nối tri thức300.000 ₫ 3 K 1.5 K lượt tải
-
Bộ 20 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án200.000 ₫ 2.6 K 1.3 K lượt tải
-
Bộ trắc nghiệm Toán 7 Chân trời sáng tạo (cả năm) có đáp án200.000 ₫ 9.9 K 4.9 K lượt tải
-
Bộ 27 đề thi cuối kì 1 Toán 7 Kết nối tri thức có đáp án150.000 ₫ 20.1 K 10 K lượt tải
-
Đề cương ôn tập Giữa kì 1 Toán 7 Kết nối tri thức80.000 ₫ 2.6 K 1.3 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 7
Xem thêm-
Bộ 6 đề thi giữa kì 1 Tiếng Anh 7 Global success có đáp án100.000 ₫ 36 K 18 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Lịch sử & Địa lý 7 Kết nối tri thức có đáp án70.000 ₫ 5.1 K 2.5 K lượt tải
-
Bộ 7 đề thi giữa kì 1 KHTN 7 Chân trời sáng tạo có đáp án100.000 ₫ 5.5 K 2.8 K lượt tải
-
Đề luyện thi HSG Tiếng Anh 7 | Đề thi học sinh giỏi Anh 7250.000 ₫ 17.7 K 8.9 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Ngữ Văn 7 Kết nối tri thức có đáp án150.000 ₫ 16.8 K 8.4 K lượt tải
-
Bộ 4 đề thi giữa kì 1 Tin học 7 Kết nối tri thức có đáp án70.000 ₫ 6.4 K 3.2 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Ngữ Văn 7 Chân trời sáng tạo có đáp án150.000 ₫ 10.8 K 5.4 K lượt tải
-
Bộ 7 đề thi giữa kì 1 KHTN 7 Kết nối tri thức có đáp án100.000 ₫ 9.2 K 4.6 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 8. Đường vuông góc và đường xiên
Câu 1. Cho hình bên.
Độ dài đoạn thẳng nào ngắn nhất?
A. AB;
B. AD;
C. AE;
D. AC.
Câu 2. Trong hình bên có bao nhiêu đường xiên kẻ từ các điểm M, P, Q đến đường
thẳng NT?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A. 2;
B. 3;
C. 4;
D. 5.
Câu 3. Cho ∆ABC có AD là đường cao như hình bên.
Trong ba cạnh AB, AD, AC, cạnh nào ngắn nhất?
A. AD;
B. AB;
C. AC;
D. Không thể so sánh được.
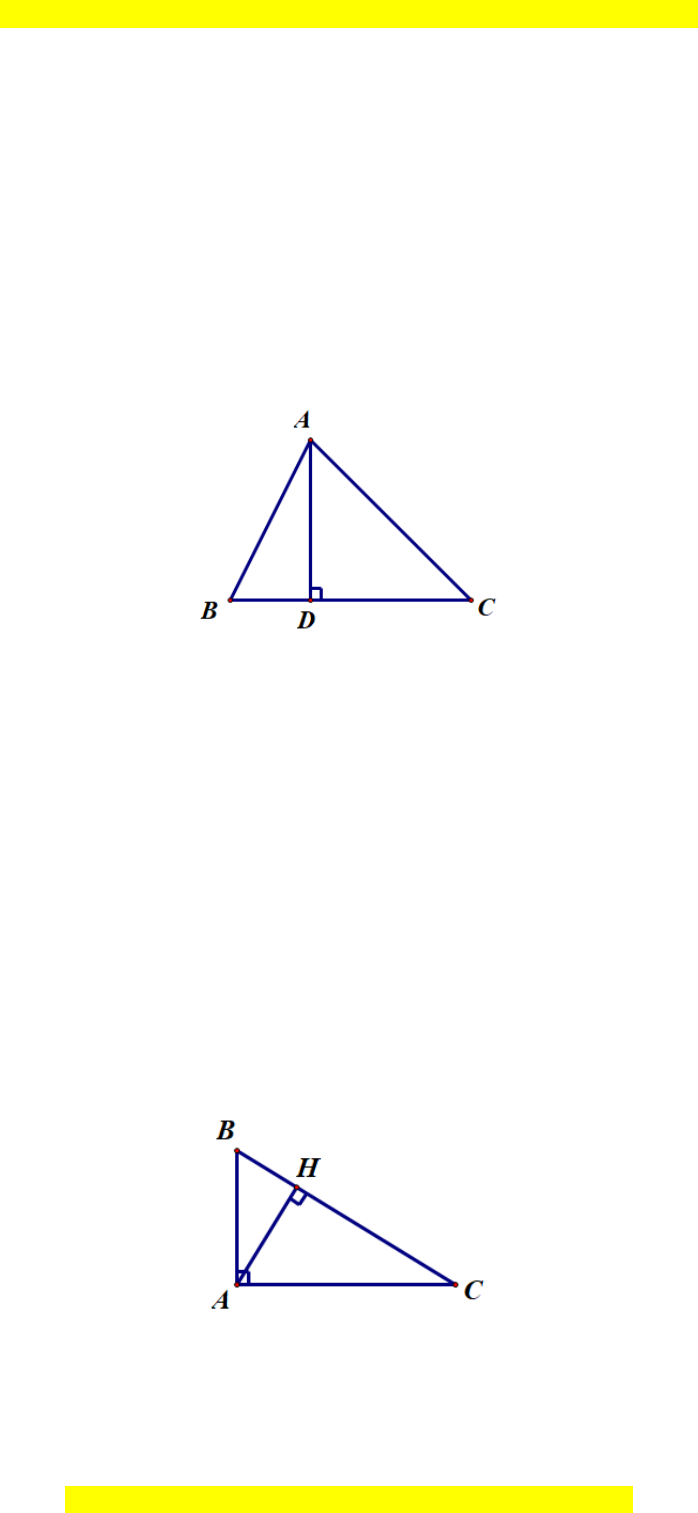
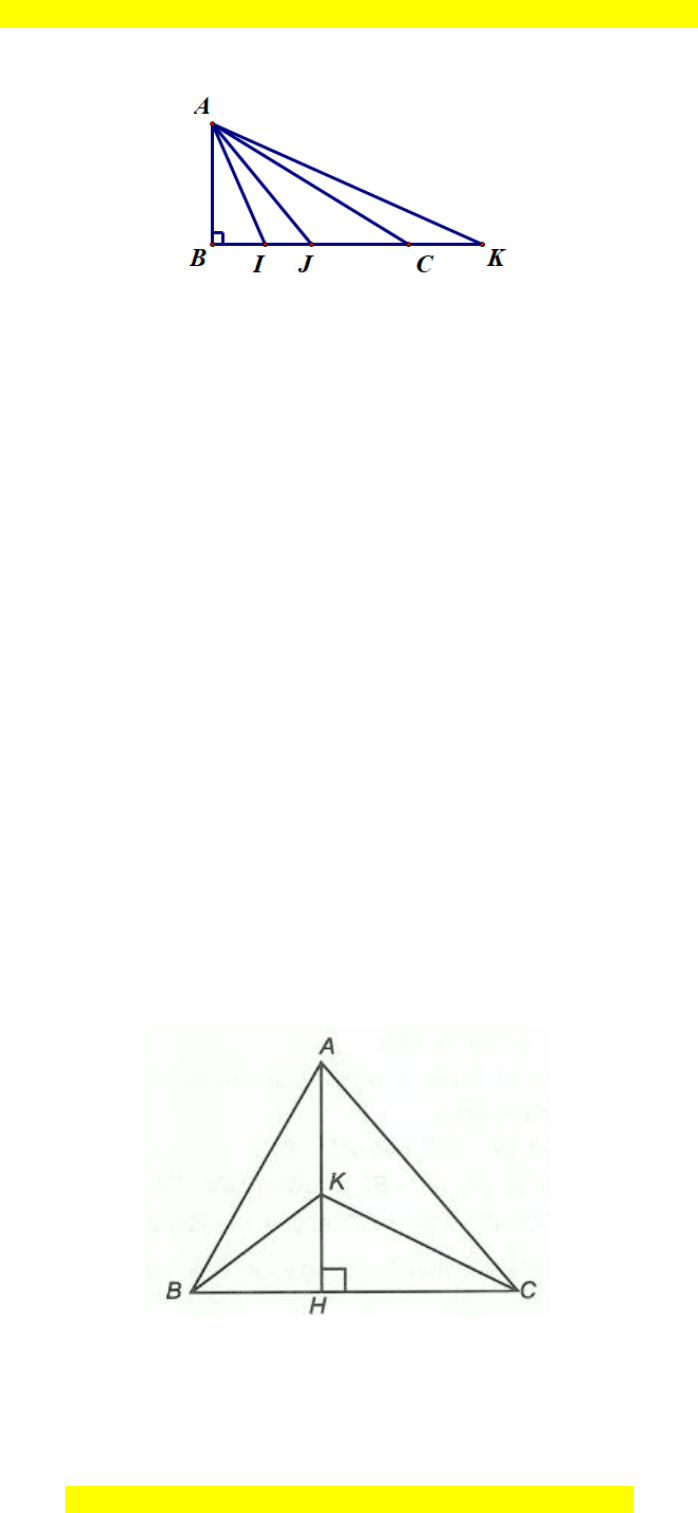
Câu 4. Cho ∆ABC vuông tại A. Kẻ AH ⊥ BC (H ∈ BC). Có bao nhiêu đường
vuông góc kẻ từ các điểm A, B, C đến các đường thẳng có trong hình bên?
A. 3;
B. 4;
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C. 5;
D. 7.
Câu 5. Cho ∆ABC vuông tại B. Trên đường thẳng BC lấy điểm I, J, K sao cho AI
< AJ < AK. Hỏi B là hình chiếu của các điểm nào lên đường thẳng AB?
A. C, J, A, K;
B. A, C, K, J;
C. I, J, C, A;
D. I, J, C, K.
Câu 6. Cho ∆ABC (AB < AC), đường cao AH (H ∈ BC). Lấy điểm K bất kì thuộc
AH (K ≠ H). Trong các đoạn thẳng AB, AC, AH, BK, CK, KH, đoạn thẳng nào
ngắn nhất?
A. AH;
B. KH;
C. BK;
D. CK.
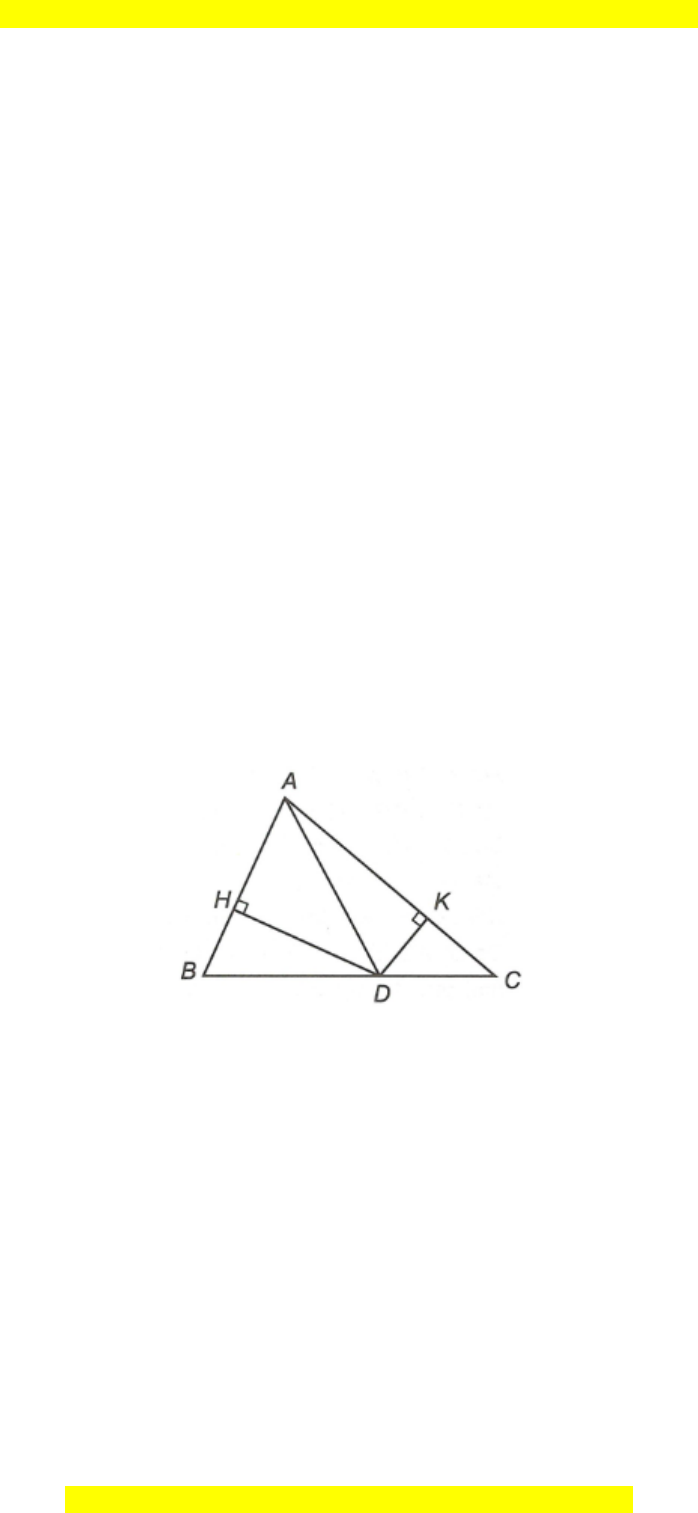
Câu 7. Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường
vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC.
So sánh BC và tổng DH + DK.
A. DH + DK > BC;
B. DH + DK < BC;
C. DH + DK = BC;
D. Không thể so sánh được.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 8. Cho ∆ABC có
ABC 30=
,
ACB 70=
. Gọi H là chân đường vuông góc
kẻ từ B. Khẳng định nào sau đây đúng?
A. HA > AC;
B. HA < AC;
C. HA = AC;
D.
BAC 70=
.
Câu 9. Cho ∆ABC. Vẽ AD ⊥ BC, BE ⊥ AC, CF ⊥ AB (D ∈ BC, E ∈ AC, F ∈
AB). So sánh AD + BE + CF và chu vi C của ∆ABC.
A. AD + BE + CF = C;
B. AD + BE + CF < C;
C. AD + BE + CF > C;
D. Không thể so sánh được.
Câu 10. Cho ∆MNP vuông tại M. Vẽ MH ⊥ NP tại H. Trên cạnh NP lấy điểm E
sao cho NE = MN. Trên cạnh MP lấy điểm F sao cho MF = MH. Khoảng cách từ
E đến đường thẳng MP là đoạn thẳng:
A. EM;
B. EF;
C. EP;
D. EN.
Câu 11. Cho ∆ABC vuông tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy
điểm F. So sánh độ dài các cạnh EA và BF.
A. EA = BF;
B. EA < BF;
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C. EA > BF;
D. Không thể so sánh được.
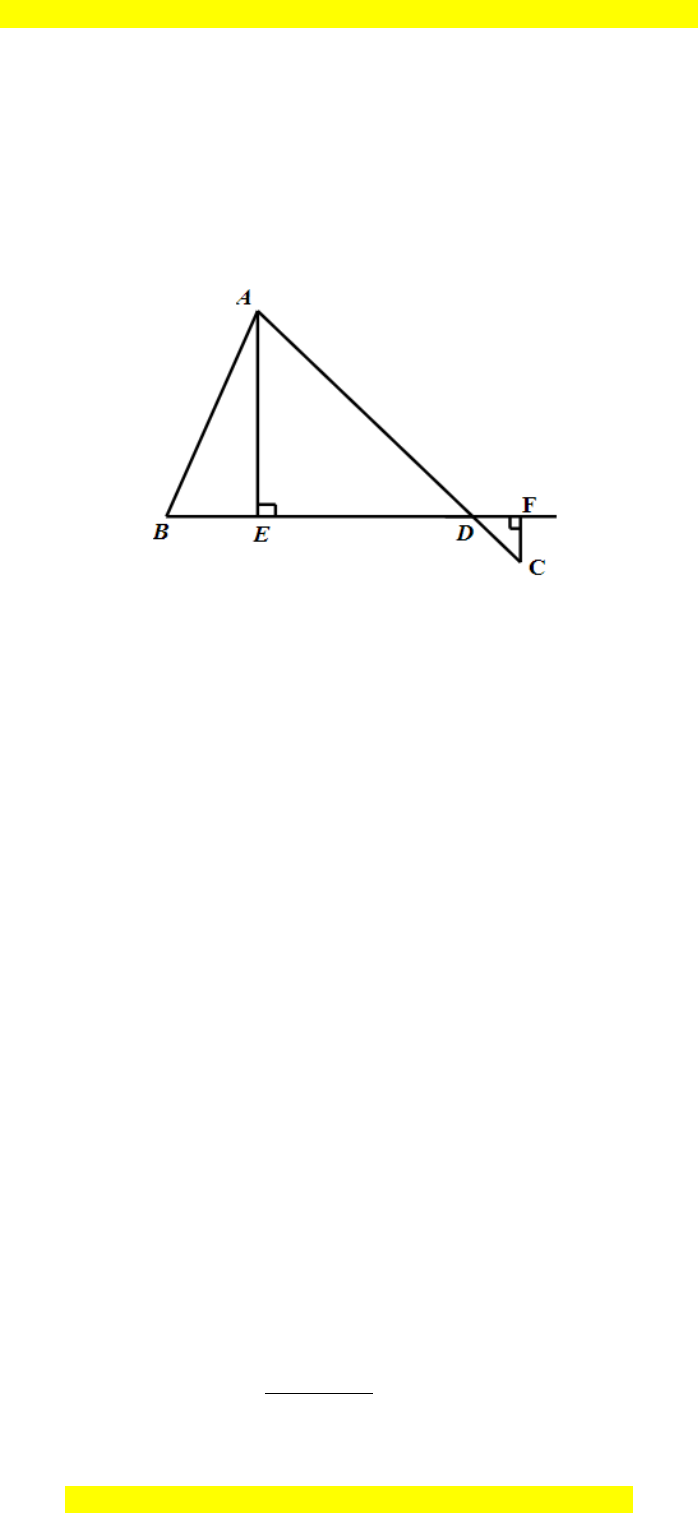
Câu 12. Cho hình vẽ bên.
So sánh AC và AE + CF.
A. AC > AE + CF;
B. AC < AE + CF;
C. AC = AE + CF;
D. Không thể so sánh được.
Câu 13. Cho ∆ABC vuông tại A, biết AB = 10 cm. Trên đường thẳng AC, lấy hai
điểm E và F sao cho AE = 3 cm, AF = 5 cm. So sánh CA, CB, CE và CF.
A. CF < CE < CA < CB;
B. CB < CF < CA < CE;
C. CE < CA < CB < CF;
D. CF < CA < CE < CB.
Câu 14. Cho ∆ABC vuông tại A. Gọi M là trung điểm AC. Kẻ AH ⊥ BM tại H,
CK ⊥ BM tại K. So sánh AB và
BH BK
2
+
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
BH BK
AB
2
+
;
B.
BH BK
AB
2
+
;
C.
BH BK
AB
2
+
=
;
D. Không thể so sánh được.
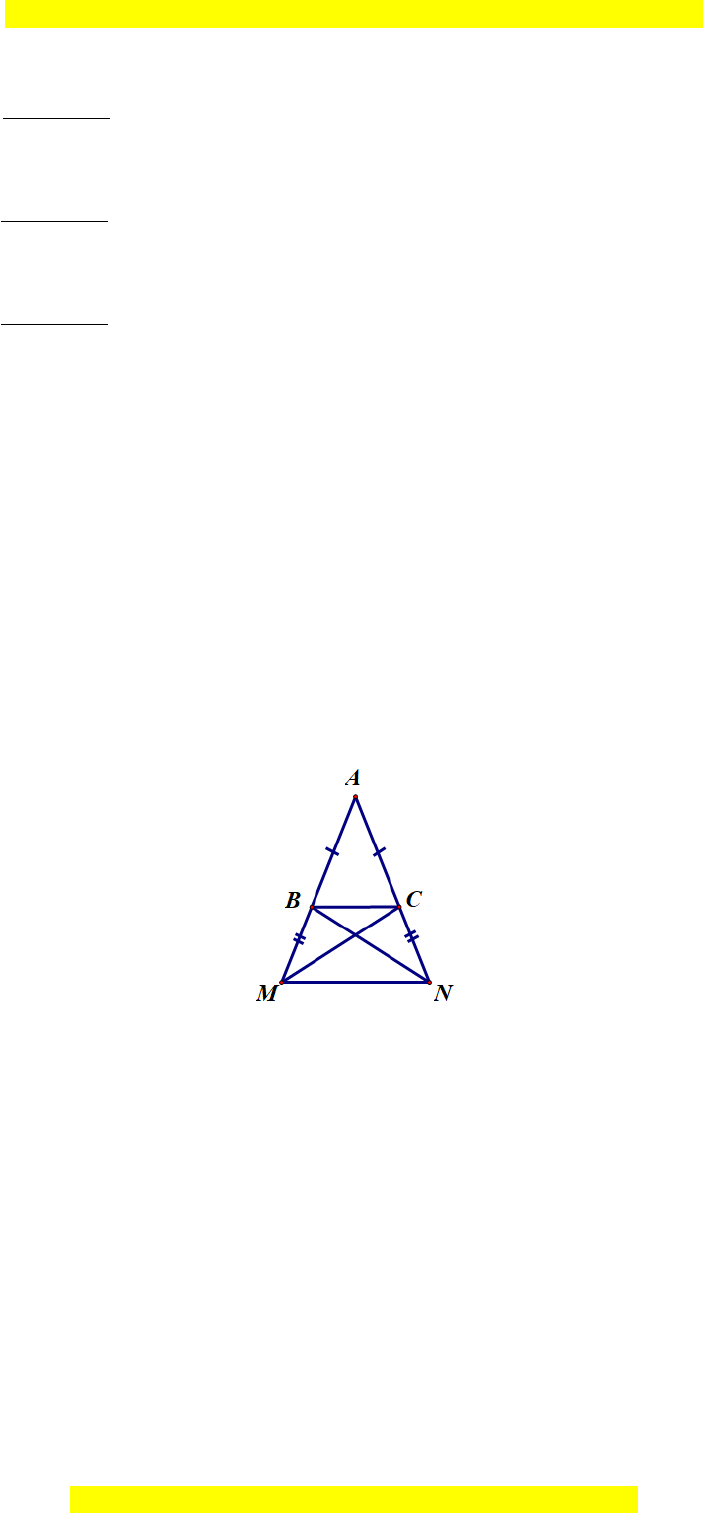
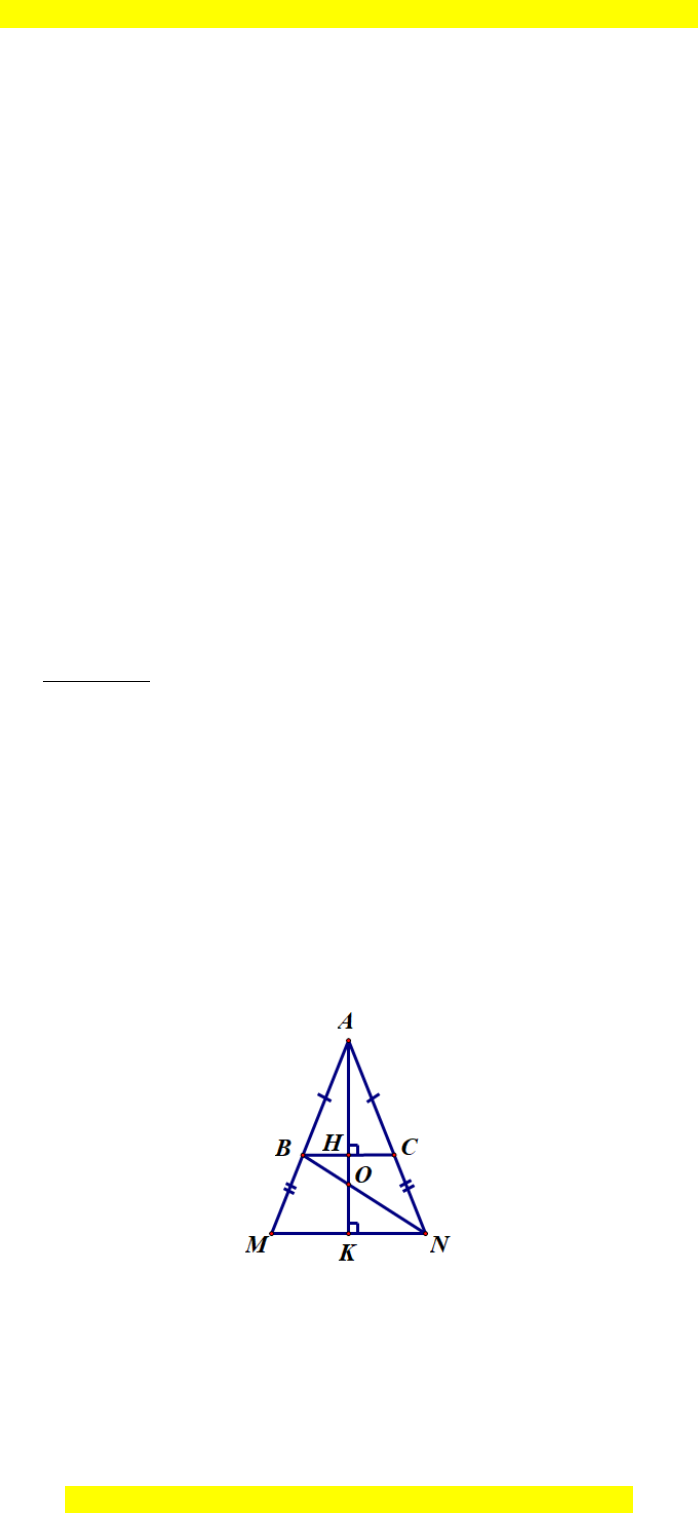
Câu 15. Hình bên mô tả một chiếc thang đứng hình chữ A là tam giác ABC. Do
chiếc thang hơi ngắn nên một người thợ đã nối thêm 2 thanh gỗ bằng nhau BM
và CN lần lượt vào hai cạnh AB, AC. Để giữ thăng bằng và cố định chiếc thang
nên người thợ này muốn đóng thêm 2 thanh gỗ bằng nhau là BN và CM. Biết BC
= 0,6 m, MN = 0,9 m. Em hãy cho biết độ dài thanh gỗ BN cần dài ít nhất bao
nhiêu là hợp lí?
A. 0,3 m;
B. 0,6 m;
C. 0,75 m;
D. 0,8 m.
LỜI GIẢI CHI TIẾT
Câu 1.
Hướng dẫn giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đáp án đúng là: A
Đoạn thẳng AB là đường vuông góc kẻ từ O đến đường thẳng BC.
Các đoạn thẳng AD, AE, AC là đường xiên kẻ từ A đến đường thẳng BC.
Do đó đoạn AB ngắn nhất.
Vậy ta chọn đáp án A
Câu 2.
Hướng dẫn giải
Đáp án đúng là: C
Các đường thẳng không vuông góc với NT đều là đường xiên từ các điểm không
thuộc đường thẳng NT đến đường thẳng NT.
Các đoạn thẳng MN, MT là các đường xiên kẻ từ điểm M đến đường thẳng NT.
Đoạn thẳng PT là đường xiên kẻ từ điểm P đến đường thẳng NT.
Đoạn thẳng QS là đường xiên kẻ từ điểm Q đến đường thẳng NT.
Do đó có 4 đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT.
Vậy ta chọn đáp án C.
Câu 3.
Hướng dẫn giải
Đáp án đúng là: A
Ta có đoạn thẳng AD là đường vuông góc kẻ từ điểm A đến đường thẳng BC; các
đoạn thẳng AB, AC là các đường xiên kẻ từ điểm A đến đường thẳng BC.
Do đó đoạn thẳng AD ngắn nhất.
Vậy ta chọn đáp án A.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 4.
Hướng dẫn giải
Đáp án đúng là: C
Ta xét điểm A:
Đoạn thẳng AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC.
Do đó có 1 đường vuông góc kẻ từ điểm A trong hình trên (1).
Ta xét điểm B:
+) Đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC.
+) Đoạn thẳng BH là đường vuông góc kẻ từ điểm B đến đường thẳng AH.
Do đó có 2 đường vuông góc kẻ từ điểm B trong hình trên (2).
Ta xét điểm C:
+) Đoạn thẳng CA là đường vuông góc kẻ từ điểm C đến đường thẳng AB.
+) Đoạn thẳng CH là đường vuông góc kẻ từ điểm C đến đường thẳng AH.
Do đó có 2 đường vuông góc kẻ từ điểm C trong hình trên (3).
Từ (1), (2), (3), ta được 5 đường vuông góc thỏa yêu cầu bài toán.
Vậy ta chọn đáp án C.
Câu 5.
Hướng dẫn giải
Đáp án đúng là: D
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Trong hình trên, ta thấy CB ⊥ AB (∆ABC vuông tại B).
Do đó B là hình chiếu của C lên đường thẳng AB.
Ta có I, J, K đều thuộc đường thẳng BC.
Mà BC ⊥ AB.
Do đó IB ⊥ AB hay JB ⊥ AB hay KB ⊥ AB.
Suy ra B là hình chiếu của I, J, K lên đường thẳng AB.
Khi đó ta có B là hình chiếu của các điểm I, J, K, C lên đường thẳng AB.
Vậy ta chọn đáp án D.
Câu 6.
Hướng dẫn giải
Đáp án đúng là: B
Ta có đoạn thẳng AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC; các
đoạn thẳng AB, AC là các đường xiên kẻ từ điểm A đến đường thẳng BC.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó AH là đoạn thẳng ngắn nhất trong ba đoạn thẳng AB, AC và AH (1).
Ta có đoạn thẳng KH là đường vuông góc kẻ từ điểm K đến đường thẳng BC; các
đoạn thẳng KB, KC là các đường xiên kẻ từ điểm K đến đường thẳng BC.
Do đó KH là đoạn thẳng ngắn nhất trong ba đoạn thẳng KB, KC và KH (2).
Vì K thuộc AH (giả thiết) nên KH < AH (3).
Từ (1), (2), (3), ta suy ra KH là đoạn thẳng ngắn nhất trong các đoạn thẳng AB,
AC, AH, BK, CK, KH.
Vậy ta chọn đáp án B.
Câu 7.
Hướng dẫn giải
Đáp án đúng là: B
Ta có DH là đường vuông góc kẻ từ điểm D đến đường thẳng AB; DB là đường
xiên kẻ từ điểm D đến đường thẳng AB.
Ta suy ra DH < DB (1).
Tương tự, ta có DK là đường vuông góc kẻ từ điểm D đến đường thẳng AC; DC
là đường xiên kẻ từ điểm D đến đường thẳng AC.
Ta suy ra DK < DC (2).
Từ (1), (2), ta suy ra DH + DK < DB + DC = BC.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Khi đó ta có DH + DK < BC.
Vậy ta chọn đáp án B.
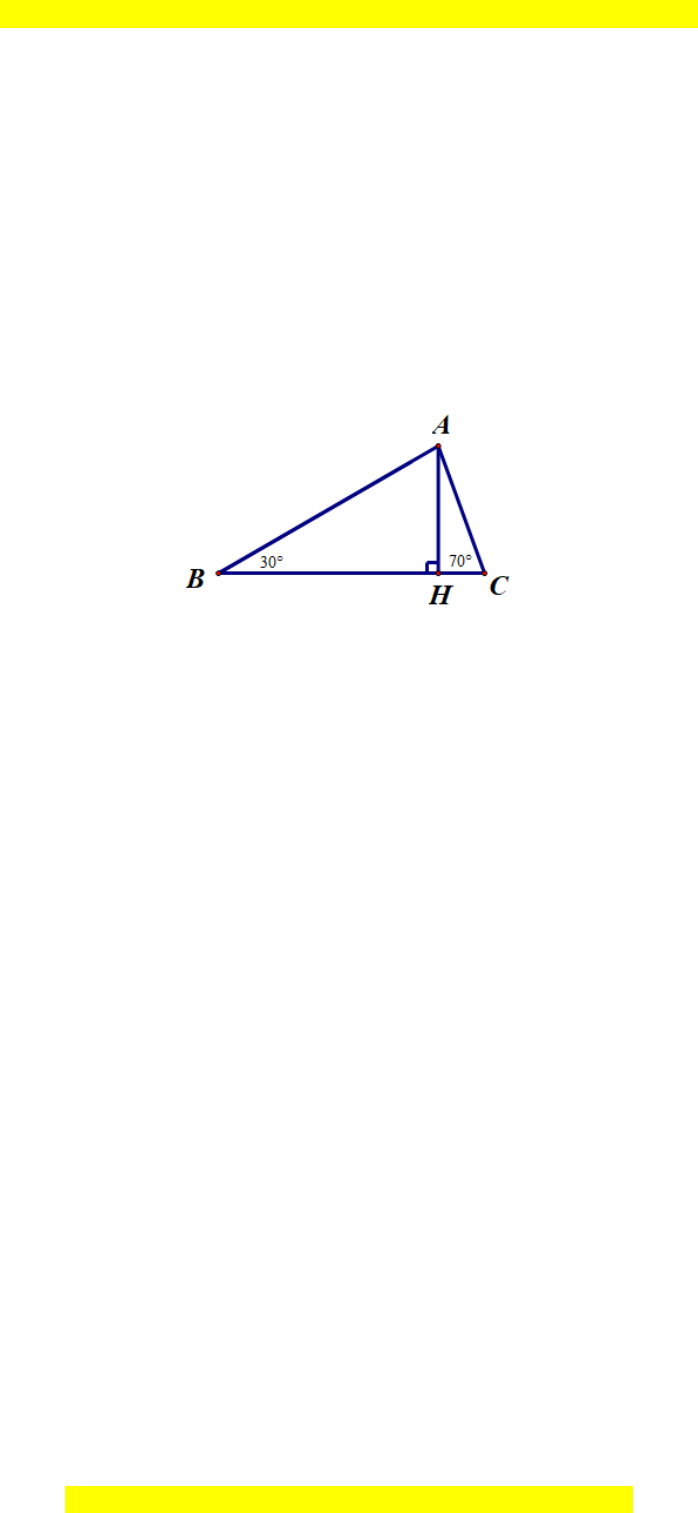
Câu 8.
Hướng dẫn giải
Đáp án đúng là: B
Ta xét đáp án D:
∆ABC có:
BAC ABC ACB 180+ + =
(định lí tổng ba góc của một tam giác)
Suy ra
BAC 180 ABC ACB 180 30 70 80 70= − − = − − =
.
Do đó đáp án D sai.
Ta xét đáp án A, B, C:
Ta có AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC; AC là một
đường xiên kẻ từ điểm A đến đường thẳng AC.
Do đó AH < AC.
Suy ra đáp án B đúng, đáp án A, C sai.
Vậy ta chọn đáp án B.
Câu 9.
Hướng dẫn giải
Đáp án đúng là: B
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta thấy AD là đường vuông góc kẻ từ điểm A đến đường thẳng BC và AB là một
đường xiên kẻ từ điểm A đến đường thẳng BC.
Do đó AD < AB (1).
Tương tự, ta có CF là đường vuông góc kẻ từ điểm C đến đường thẳng AB và CA
là một đường xiên kẻ từ điểm C đến đường thẳng AB.
Do đó CF < AC (2).
Tương tự, ta có BE là đường vuông góc kẻ từ điểm B đến đường thẳng AC và BC
là một đường xiên kẻ từ điểm B đến đường thẳng AC.
Do đó BE < BC (3).
Lấy (1) + (2) + (3) vế theo vế, ta được:
AD + CF + BE < AB + AC + BC.
Do đó AD + BE + CF < C.
Vậy ta chọn đáp án B.
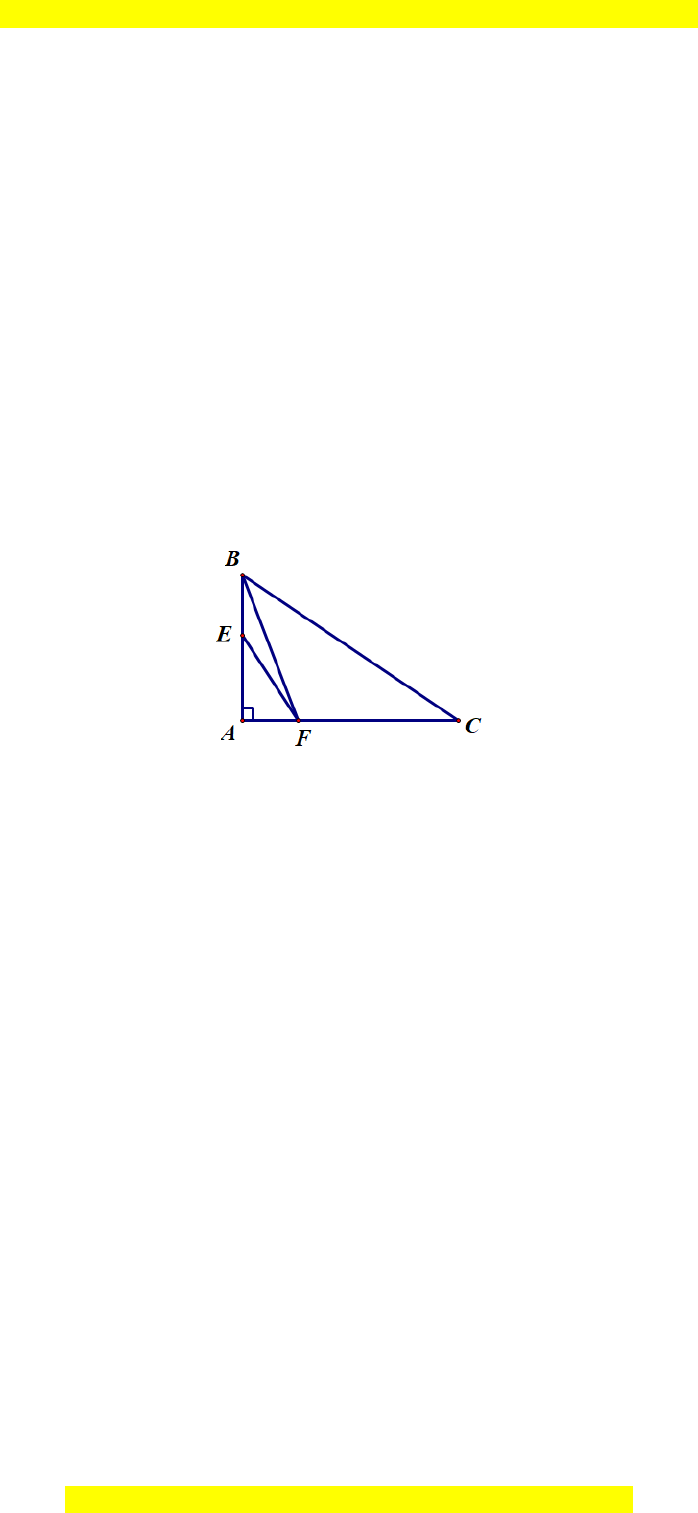
Câu 10.
Hướng dẫn giải
Đáp án đúng là: B
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có NE = MN (giả thiết).
Suy ra ∆MNE cân tại N.
Do đó
NME NEM=
(1).
Vì ∆MNP vuông tại A nên
NMP 90=
.
Suy ra
NME EMF 90+ =
(2).
Từ (1), (2), ta suy ra
NEM EMF 90+ =
(*).
∆MHE vuông tại H:
HME NEM 90+ =
(**).
Từ (*), (**), ta suy ra
EMF HME=
.
Xét ∆HME và ∆FME, có:
ME là cạnh chung.
EMF HME=
(chứng minh trên).
MH = MF (giả thiết).
Do đó ∆HME = ∆FME (c.g.c).
Suy ra
MHE MFE=
(cặp góc tương ứng).
Mà
MHE 90=
(do MH ⊥ HE).
Suy ra
MFE 90=
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó EF ⊥ MF hay EF ⊥ MP.
Khi đó ta có EF là đường vuông góc kẻ từ điểm E đến đường thẳng MP.
Do đó đoạn thẳng EF là khoảng cách từ E đến đường thẳng MP.
Vậy ta chọn đáp án B.
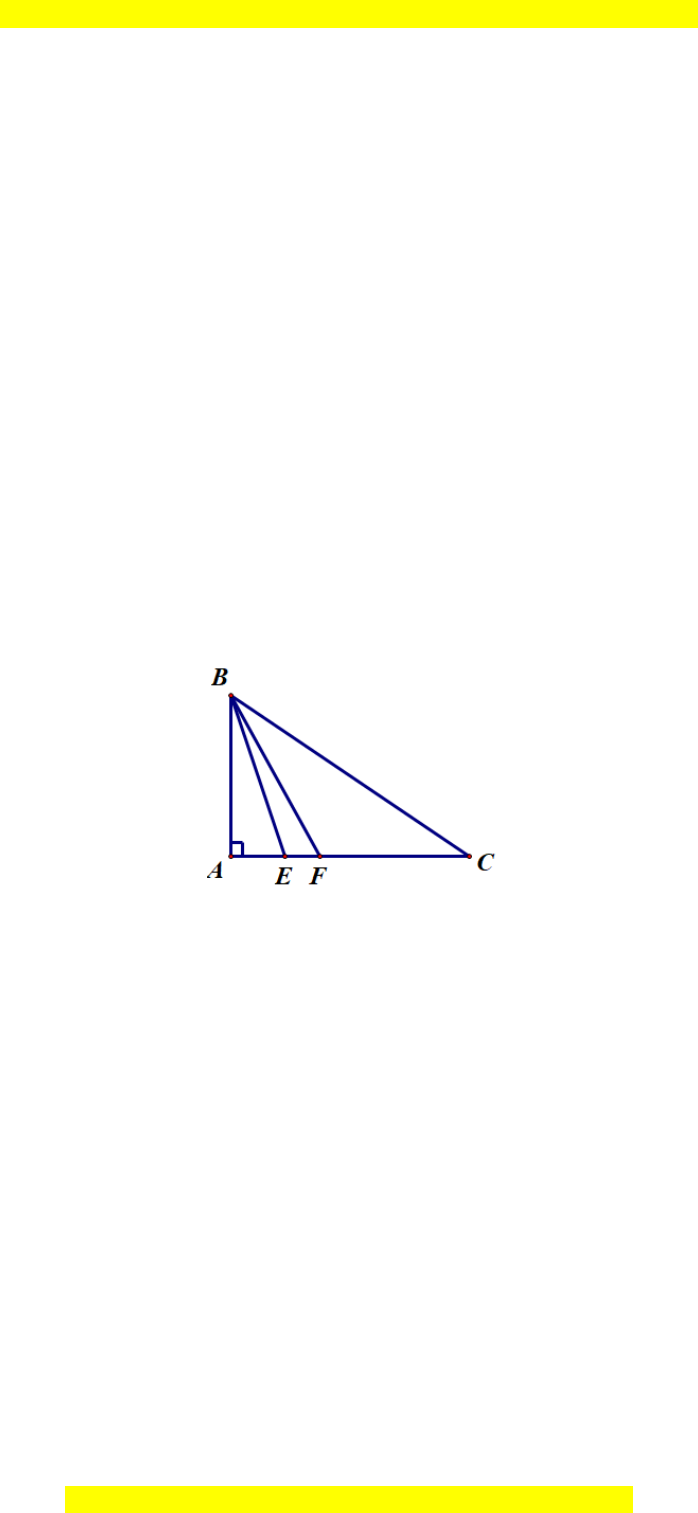
Câu 11.
Hướng dẫn giải
Đáp án đúng là: B
Ta có đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC;
đoạn thẳng BF là đường xiên kẻ từ điểm B đến đường thẳng AC.
Do đó BA < BF (1).
Vì E thuộc cạnh AB (giả thiết) nên EA < BA (2).
Từ (1), (2), ta suy ra EA < BA < BF.
Vậy ta chọn đáp án B.
Câu 12.
Hướng dẫn giải
Đáp án đúng là: A
Ta có đoạn thẳng AE là đường vuông góc kẻ từ điểm A đến đường thẳng EF; đoạn
thẳng AD là đường xiên kẻ từ điểm A đến đường thẳng EF.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó AE < AD (1).
Ta có đoạn thẳng CF là đường vuông góc kẻ từ điểm C đến đường thẳng EF; đoạn
thẳng CD là đường xiên kẻ từ điểm C đến đường thẳng EF.
Do đó CF < CD (2).
Lấy (1) + (2) vế theo vế, ta được AE + CF < AD + CD = AC.
Vậy ta chọn đáp án A.
Câu 13.
Hướng dẫn giải
Đáp án đúng là: A
Ta thấy CA ⊥ AB tại A.
Do đó CA là đường vuông góc kẻ từ điểm C đến đường thẳng AB và BC là đường
xiên kẻ từ điểm C đến đường thẳng AB.
Suy ra CA < CB (1).
Ta có E ∈ AC và AE = 3 cm.
Suy ra CE = AC – AE = AC – 3.
Do đó CE < AC (2).
Ta có F ∈ AC và AF = 5 cm.
Suy ra CF = AC – AF = AC – 5 = (AC – 3) – 2.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Mà CE = AC – AE = AC – 3 (chứng minh trên).
Do đó CF = CE – 2
Suy ra CF < CE (3).
Từ (1), (2), (3), ta suy ra CF < CE < CA < CB.
Vậy ta chọn đáp án A.
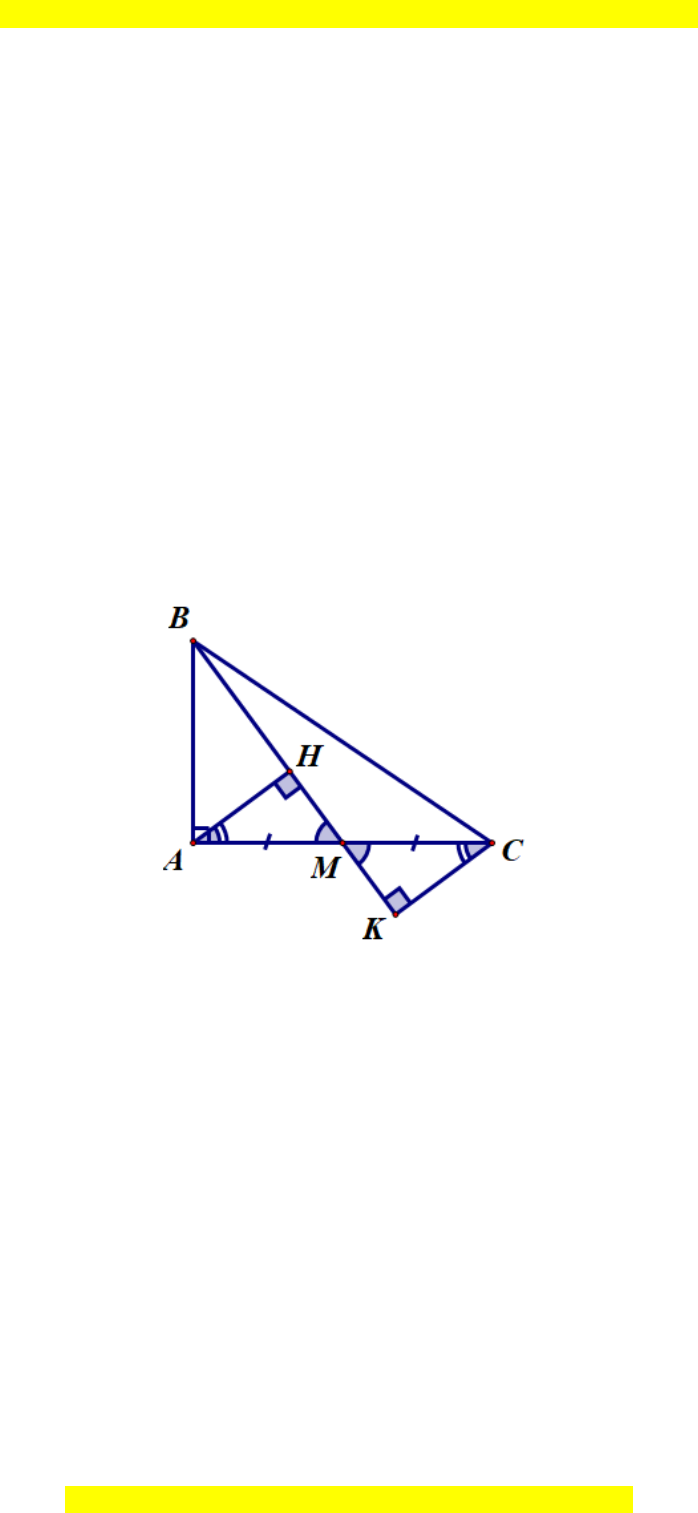
Câu 14.
Hướng dẫn giải
Đáp án đúng là: B
Ta có AH ⊥ BM (giả thiết) và CK ⊥ BM (giả thiết).
Suy ra AH // CK.
Do đó
HAM KCM=
(cặp góc so le trong).
Xét ∆HAM và ∆KCM, có:
HMA KMC=
(hai góc đối đỉnh).
MA = MC (M là trung điểm AC).
HAM KCM=
(chứng minh trên).
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó ∆HAM = ∆KCM (g.c.g).
Suy ra MH = MK (cặp cạnh tương ứng).
Ta có đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC;
đoạn thẳng BM là đường xiên kẻ từ điểm B đến đường thẳng AC.
Suy ra BA < BM.
Do đó BA < BH + HM (1) và BA < BK – MK (2).
Lấy (1) + (2) vế theo vế ta được 2BA < BH + HM + BK – MK.
Mà HM = MK (chứng minh trên).
Do đó 2AB < BH + BK.
Suy ra
BH BK
AB
2
+
.
Vậy ta chọn đáp án B.
Câu 15.
Hướng dẫn giải
Đáp án đúng là: D
Ta có AB = AC (do ∆ABC cân tại A) và BM = CN (giả thiết).
Suy ra AB + BM = AC + CN.
Do đó AM = AN.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Suy ra ∆AMN cân tại A.
Vì vậy
AMN ANM=
.
Ta có
MAN AMN ANM 180+ + =
(tổng ba góc trong một tam giác).
Suy ra
2AMN 180 MAN= −
.
Do đó
180 MAN
AMN
2
−
=
(1).
Ta có ∆ABC cân tại A.
Suy ra
ABC ACB=
.
Ta có
BAC ABC ACB 180+ + =
(tổng ba góc trong một tam giác).
Suy ra
2ABC 180 BAC= −
Do đó
180 MAN
ABC
2
−
=
(2).
Từ (1), (2), ta suy ra
AMN ABC=
.
Mà hai góc này ở vị trí đồng vị.
Khi đó ta có BC // MN.
Kẻ AH ⊥ BC tại H. Suy ra AH ⊥ MN
Giả sử AH ⊥ MN tại K.
Xét ∆ABH và ∆ACH, có:
AHB AHC 90= =
.
ABC ACB=
(do ∆ABC cân tại A).
AB = AC (do ∆ABC cân tại A).
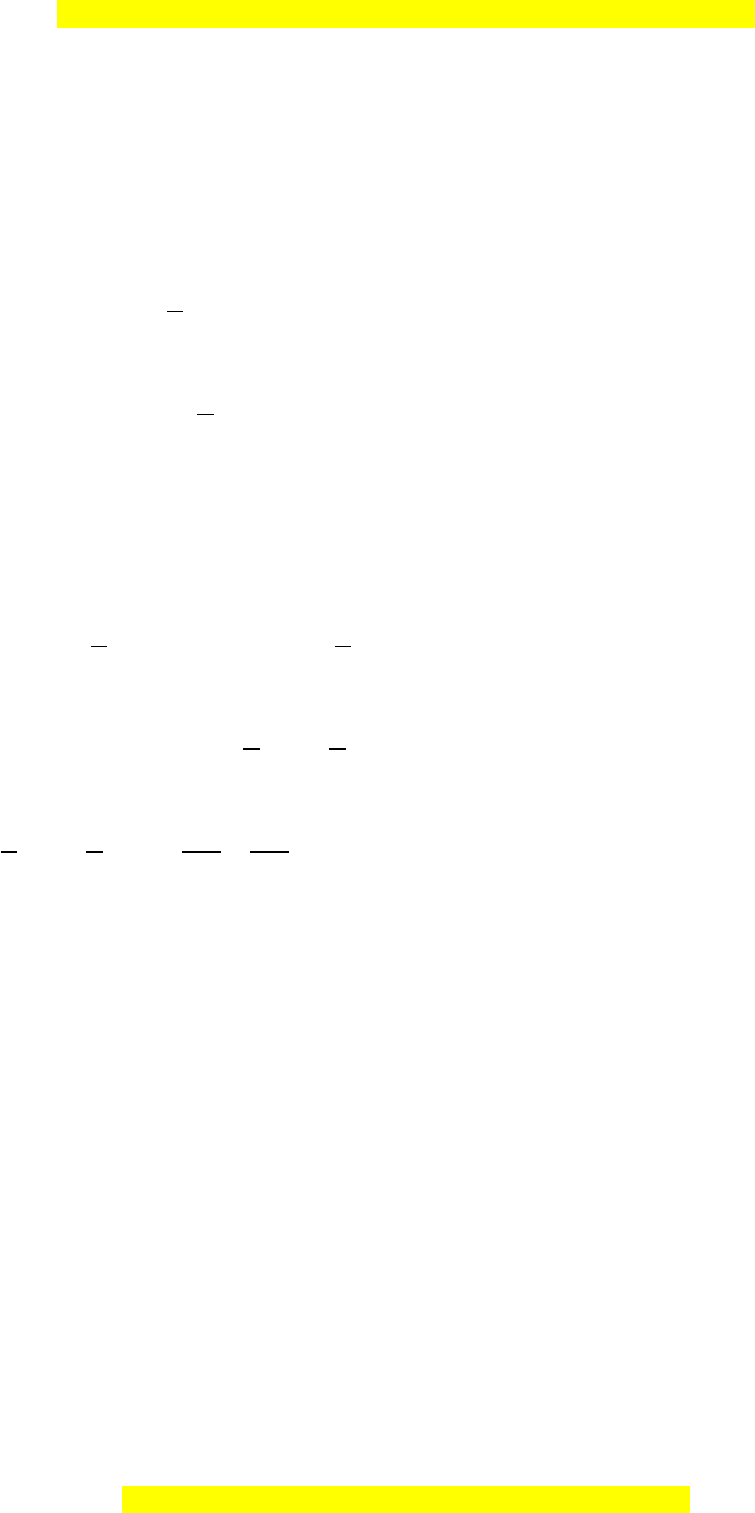
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Do đó ∆ABH = ∆ACH (cạnh huyền – góc nhọn).
Suy ra HB = HC (cặp cạnh tương ứng).
Do đó H là trung điểm BC.
Khi đó ta có
1
BH BC
2
=
.
Tương tự ta có
1
KN MN
2
=
.
Gọi O là giao điểm của BN và AK.
Theo quan hệ giữa đường vuông góc và đường xiên, ta có:
BO >
1
BH BC
2
=
và ON >
1
KN MN
2
=
.
Suy ra BN = BO + ON >
11
BC MN
22
+
Mà
1 1 0,6 0,9
BC MN 0,75
2 2 2 2
+ = + =
.
Do đó BN > 0,75 (m).
Vì 0,8 (m) > 0,75 (m).
Nên ta chọn đáp án D.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Nhắn tin Zalo