Bài tập Toán 11 Cánh diều (Dạy thêm - có lời giải)

CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC NG I
HÀM SỐ LƯỢNG GIÁC
VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC CHƯƠ
BÀI 1. GÓC LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC LƯỢNG GIÁC LÝ THUYẾT. I = I. GÓC LƯỢNG GIÁC
1. Góc hình học và số đo của chúng
Quan hệ giữa độ và radian   180  1 = rad và 1rad = .   180   
2. Góc lượng giác và số đo của chúng
a. Khái niệm: Trong mặt phẳng cho hai tia Ou, Ov . Nếu tia Om quay chỉ theo chiều dương
(hay chỉ theo chiều âm) từ tia Ou đến trùng với tia Ov , thì ta nói: tia Om quét một góc lượng
giác với tia đầu Ou , tia cuối Ov và kí hiệu là (Ou, Ov).
Nhận xét: Góc lượng giác (Ou, Ov) chỉ được xác định khi ta biết được chiều chuyển động quay
của tia Om từ tia đầu Ou đến tia cuối Ov . Ta quy ước: chiều quay ngược với chiều quay của
kim đồng hồ là chiều dương, chiều quay cùng với chiều quay của kim đồng hồ là chiều âm.  a
Khi tia Om quay góc a thì ta nói góc lượng giác mà tia đó quét nên có số đo a hay ( rad 180
). Vì thế, mỗi một góc lượng giác đều có 1 số đo, đơn vị đo góc lượng giác là độ hoặc radian.
Nếu góc lượng giác (Ou, Ov) có số đo là  thì ta = 
kí hiệu là sd (Ou, Ov) hoặc (Ou, Ov) = .
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC b. Tính chất:
Cho hai tia Ou, Ov thì có vô số góc lượng giác tia đầu Ou , tia cuối Ov . Mỗi góc lượng giác
như thế đều kí hiệu là (Ou, Ov). Số đo của các góc lượng giác này sai khác nhau một bội nguyên của 360 .
Hệ thức Chasles: với 3 tia Ou, O ,
v Ow bất kì ta có:
(Ou,Ov)+(Ov,Ow) = (Ou,Ow)+k.2 (k  )
II. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC LƯỢNG GIÁC
1. Đường tròn lượng giác
Đường tròn này cắt hai trục tọa độ tại bốn điểm A(1;0) A'( 1 − ;0), B(0 ) ;1 , B '(0; − ) 1 .
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác +
có số đo  là điểm M trên đường tròn lượng giác sao cho O ( O , A OM ) = .
2. Giá trị lượng giác của góc lượng giác Giả sử M ( ;
x y) là điểm trên đường tròn lượng giác, biểu diễn góc
lượng giác có số đo  .
• Hoành độ x của điểm M gọi là côsin của  và kí hiệu là cos , cos = x
• Tung độ y của điểm M gọi là sin của  và kí hiệu là sin , sin  = y  • sin
Nếu cos  0, tỉ số cos gọi là tang của  và kí hiệu là tan (người ta còn dùng kí hiệu sin  tg ): tan  = . cos  • cos
Nếu sin  0, tỉ số sin gọi là côtang của  và kí hiệu là cot (người ta còn dùng kí hiệu cos cotg ) : cot  = . sin 
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
Các giá trị sin, cos, tan, cot  được gọi là các giá trị lượng giác của cung . Chú ý:
a) Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
b) Từ định nghĩa ta suy ra:
1) sin và cos xác định với mọi   . Hơn nữa, ta có:
sin ( + k2 ) = sin, k   ; 1 −  sin 1
cos ( + k2 ) = cos, k   . 1 −  cos  1. 
2) tan xác định với mọi  
+ k (k  ). 2
3) cot xác định với mọi   k (k  ).
4) Dấu của các giá trị lượng giác của góc  phụ thuộc vào vị trí điểm biểu diễn M trên
đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
c. Giá trị lượng giác của các cung đặc biệt      0 6 4 3 2
CHUYÊN ĐỀ I – TOÁN – 11 – HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC 1 3 sin 0 2 1 2 2 2 cos 3 2 1 1 0 2 2 2 1 tan 0 1 3 Không xác định 3 1 cot Không xác định 3 1 0 3
Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau 2 2 sin  + cos  = 1 1  2 1+ tan  = ,   + k , k  2 cos  2 1 2 1+ cot  =
,   k , k  2 sin  k tan.cot  = 1,   , k  2
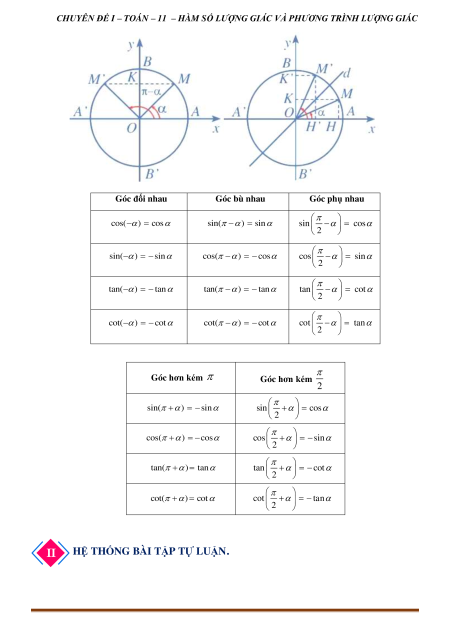
3. Giá trị lượng giác của các góc có liên quan đặc biệt