CHƯƠNG 2 HÌNH 9
Bài 1: Ở các nước xứ lạnh, vào mùa Đông thường có tuyết rơi dày đặc khắp các con
đường, trẻ em tại đây rất thích đắp hình dạng của người tuyết. Có thể xem phần thân
dưới và thân trên của người tuyết là hai hình cầu tiếp xúc nhau. Em hãy tính kích
thước của hai viên tuyết cần đắp để được một người tuyết cao 1,8m biết rằng đường
kính của phần thân dưới phải gấp đôi đường kính của phần thân trên người tuyết. Bài giải:
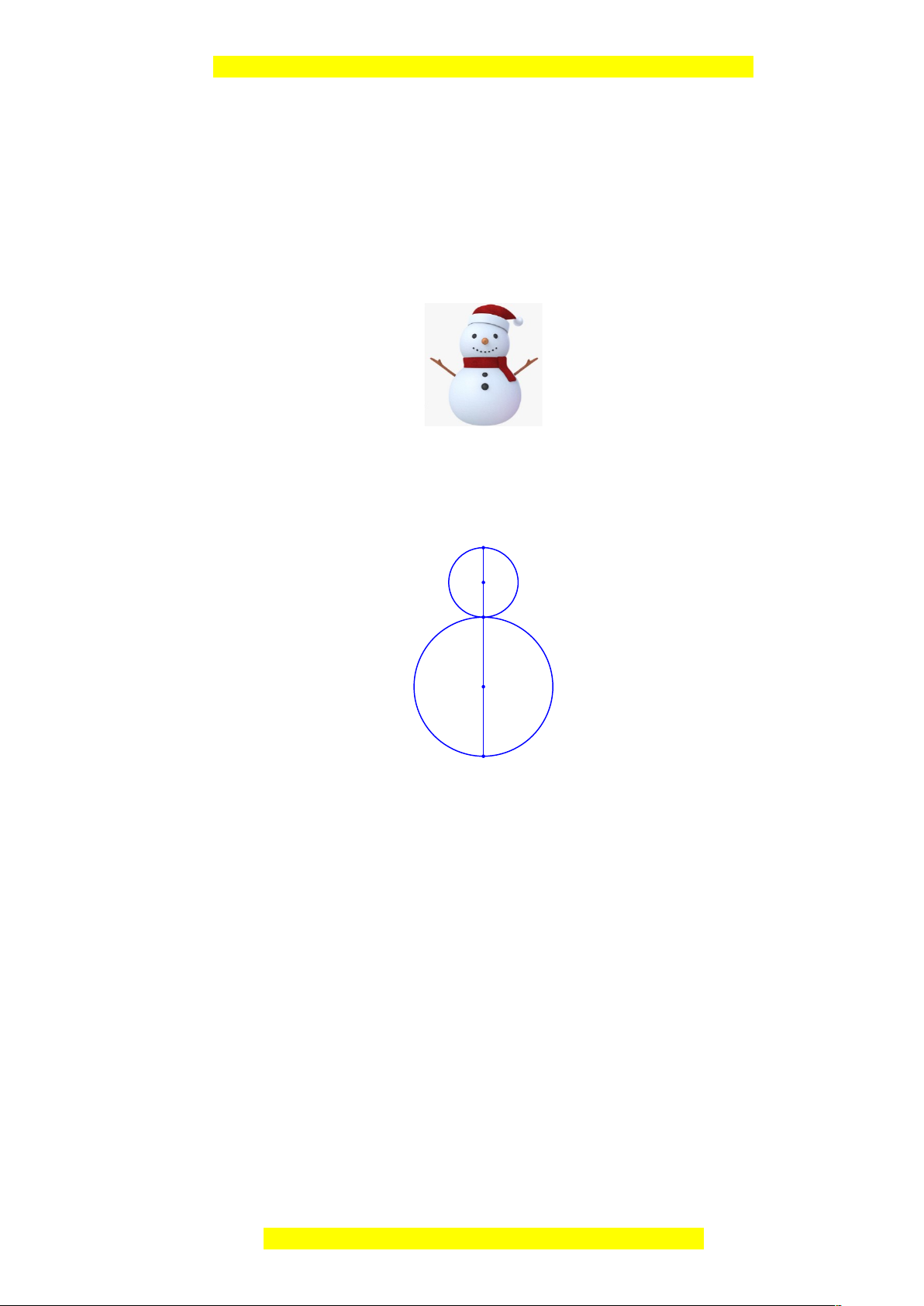
Hình vẽ minh họa bài toán: A O' O B Ta có: 1,8m = 180cm
Gọi r (cm) là bán kính của đường tròn nhỏ
⇒ Đường kính của đường tròn nhỏ là 2r (cm) (r > 0)
⇒ Đường kính của đường tròn lớn là: 2.2r = 4r (cm)
Ta có: 2r + 4r = 180 (vì (O) tiếp xúc với (O’)) ⇔6r=180⇔r =30cm
Vậy để đắp người tuyết có chiều cao là 1,8m thì ta cần đắp hai quả cầu tuyết
có đường kính lần lượt là 60cm và 120cm.
Bài 2: Một vệ tinh nhân tạo địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái
Đất một khoảng 36000km , tâm quỹ đạo vệ tinh trùng với tâm O của Trái Đất. Vệ
tinh phát tính hiệu vô tuyến theo đường thẳng đến một vị trí trên mặt đất. Hỏi vị trí xa
nhất trên Trái Đất có thể nhận tín hiệu từ vệ tinh này cách vệ tinh một khoảng là bao
nhiêu km? (ghi kết quả gần đúng chính xác đến hàng đơn vị). Biết rằng Trái Đất được
xem như một hình cầu có bán kính 6400km. Bài giải:
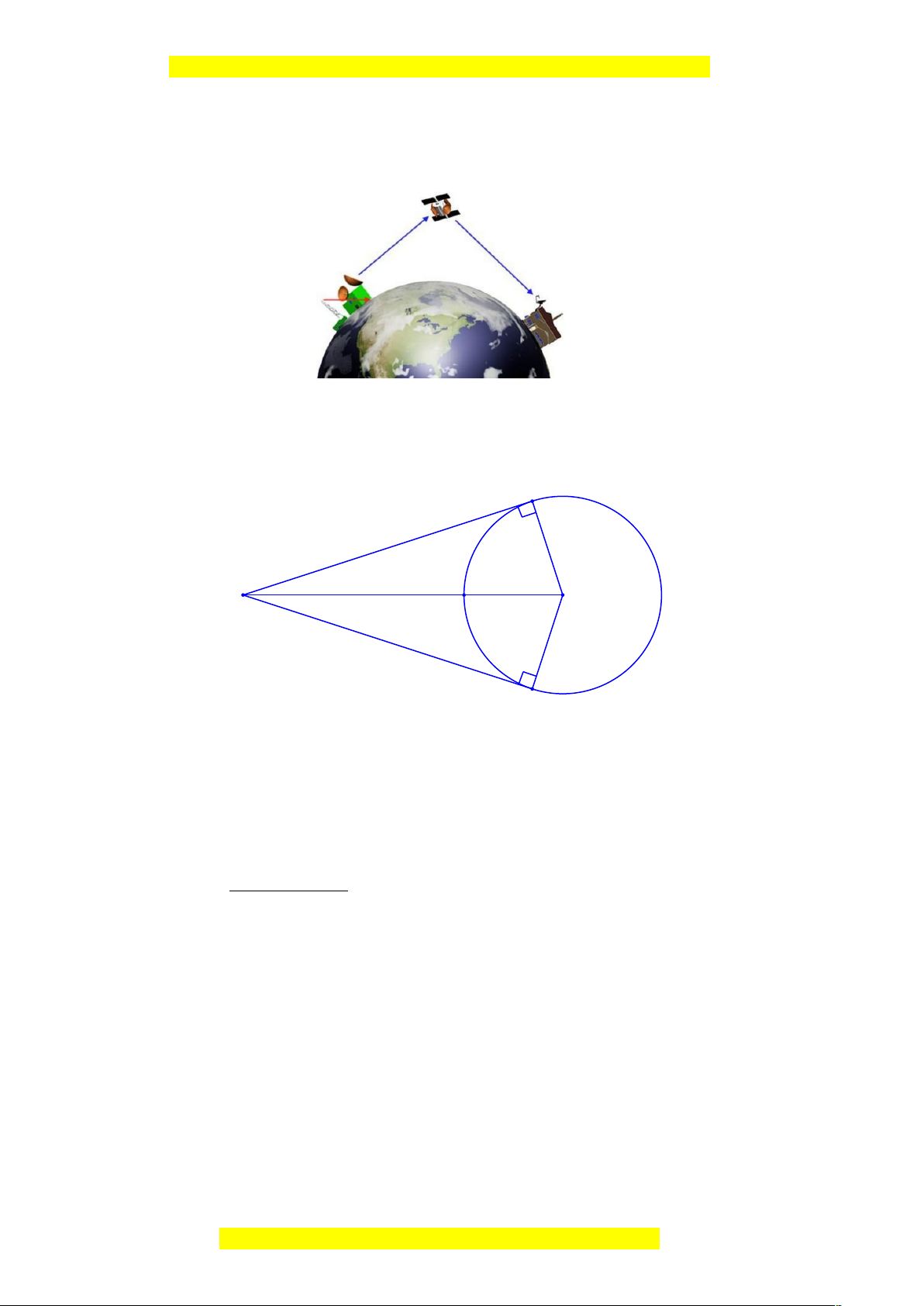
Hình vẽ minh họa bài toán: A E C O B
Ta có: CO = CE + EO = 36000 + 6400 = 42400km
Xét ∆COA vuông tại A (vì CA là tiếp tuyến của (O) nên CA ¿ OA)
⇒CO2=CA2+OA2 (định lí Pytago)
⇒CA2=CO2−OA2=424002−64002
⇒CA =√424002−64002≈41914,2km
Vậy vị trí xa nhất trên Trái Đất có thể nhận tín hiệu của vệ tinh cách vệ tinh khoảng 41914,2km
Bài 3: Khí cầu là một túi đựng không khí nóng, thường có khối lượng riêng nhỏ hơn
không khí xung quanh và nhờ vào lực đẩy Ác-si-mét có thể bay lên cao. Giả sử có thể
xem khinh khí cầu là một khối cầu và các dây nối sẽ tiếp xúc với khối cầu này. Hãy
tính chiều dài của các dây nối để khoảng cách từ buồng lái đến điểm thấp nhất của khí
cầu là 8m. Biết rằng bán kính của khối cầu này là 10m.
Bài giải:
Hình vẽ minh họa bài toán: O B C D A
Ta có: OB = OC = OD = R = 10m
⇒ OA = AD + DO = 8 + 10 = 18m
Xét ∆ABO vuông tại B (vì AB là tiếp tuyến của (O))
⇒OA2=OB2+ AB2 (định lí Pytago)
⇒ AB2=OA2− OB2=182−102=224 ⇒ AB=√224=4 √14≈15m
Vậy chiều dài của các dây nối thỏa yêu cầu bài toán là 15m.
Bài 4: Người ta muốn xây dựng một cây cầu bắc qua một hồ nước hình tròn có bán
kính 2km. Hãy tính chiều dài của cây cầu để khoảng cách từ cây cầu đến tâm của hồ nước là 1732m.
Bài giải:
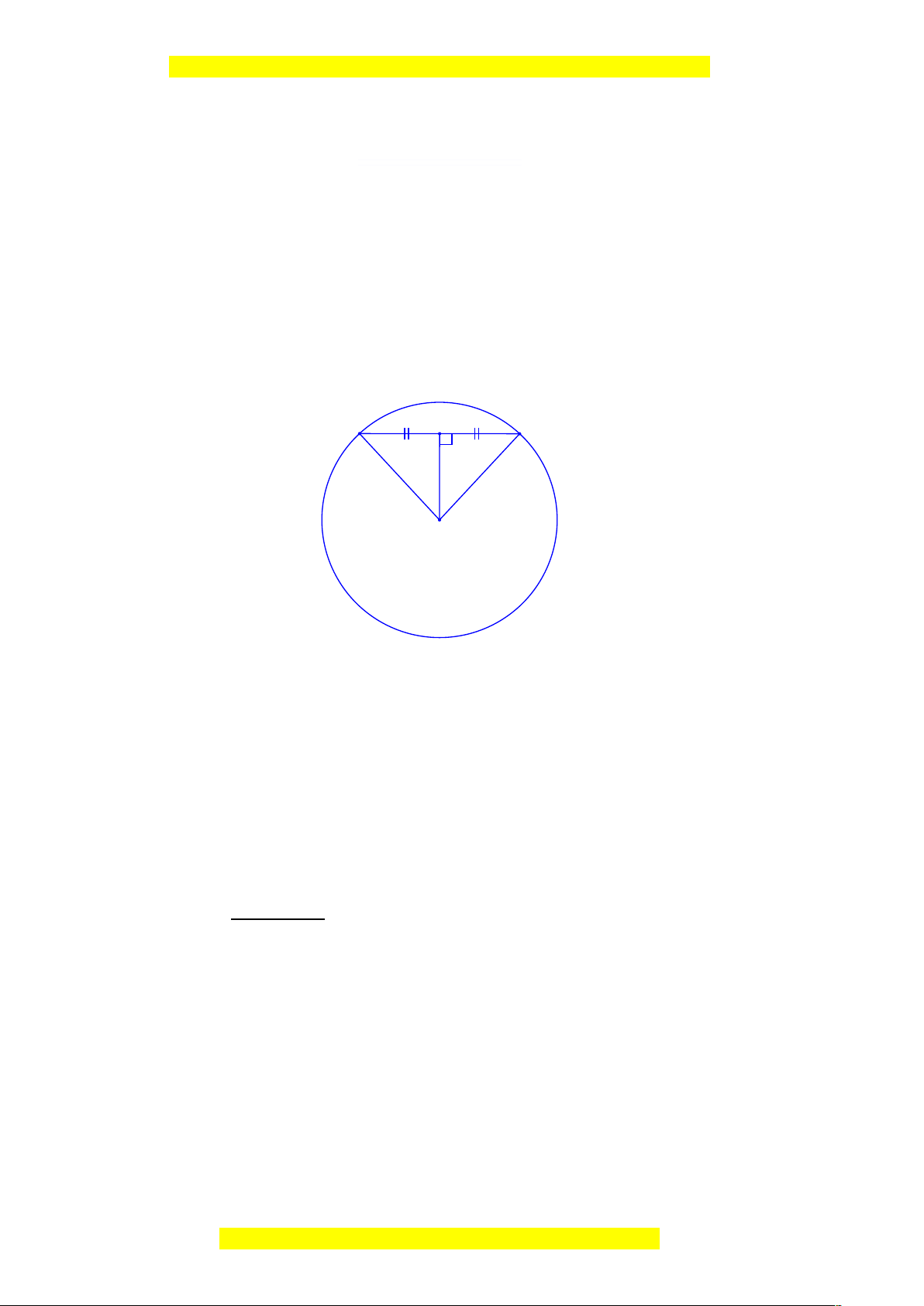
Hình vẽ minh họa bài toán: A H B O
Ta có: OA = OB = 2km (gt)
Gọi H là trung điểm của AB, dây AB không qua tâm O
⇒ OH ¿ AB tại H (liên hệ giữa đường kính và dây cung) ⇒ OH = 1732m = 1,732km (gt)
Xét ∆OHA vuông tại H
⇒OA2=OH2+AH2 (định lý Pytago) 2 ⇒ AH2=OA2−OH2=22−(1,732) 2 ⇒ AH=√22−(1,732) ≈1km
Ta có: AB=2AH=2. 1=2km (vì H là trung điểm của AB)
Vậy chiều dài của cây cầu là khoảng 2km.
Bài 5: Một bánh xe có dạng hình tròn bán kính 20cm lăn đến bức tường hợp với mặt
đất một góc 600. Hãy tính khoảng cách ngắn nhất từ tâm bánh xe đến góc tường.
Bài toán thực tế ôn vào 10 Hình học - Chương 2
1.1 K
561 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu cách giải các bài toán thực tế ôn vào lớp 10 môn Toán Hình học mới nhất năm 2022 - 2023 nhằm giúp Giáo viên có thêm tài liệu tham khảo ôn vào 10 môn Toán.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1121 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Ôn vào 10
Xem thêmTài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
CHƯƠNG 2 HÌNH 9
Bài 1: Ở các nước xứ lạnh, vào mùa Đông thường có tuyết rơi dày đặc khắp các con
đường, trẻ em tại đây rất thích đắp hình dạng của người tuyết. Có thể xem phần thân
dưới và thân trên của người tuyết là hai hình cầu tiếp xúc nhau. Em hãy tính kích
thước của hai viên tuyết cần đắp để được một người tuyết cao 1,8m biết rằng đường
kính của phần thân dưới phải gấp đôi đường kính của phần thân trên người tuyết.
Bài giải:
Hình vẽ minh họa bài toán:
O
O'
B
A
Ta có: 1,8m = 180cm
Gọi r (cm) là bán kính của đường tròn nhỏ
⇒
Đường kính của đường tròn nhỏ là 2r (cm) (r > 0)
⇒
Đường kính của đường tròn lớn là: 2.2r = 4r (cm)
Ta có: 2r + 4r = 180 (vì (O) tiếp xúc với (O’))
⇔6r=180⇔r =30cm
Vậy để đắp người tuyết có chiều cao là 1,8m thì ta cần đắp hai quả cầu tuyết
có đường kính lần lượt là 60cm và 120cm.
Bài 2: Một vệ tinh nhân tạo địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái
Đất một khoảng
36000km
, tâm quỹ đạo vệ tinh trùng với tâm O của Trái Đất. Vệ
tinh phát tính hiệu vô tuyến theo đường thẳng đến một vị trí trên mặt đất. Hỏi vị trí xa
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
nhất trên Trái Đất có thể nhận tín hiệu từ vệ tinh này cách vệ tinh một khoảng là bao
nhiêu km? (ghi kết quả gần đúng chính xác đến hàng đơn vị). Biết rằng Trái Đất được
xem như một hình cầu có bán kính 6400km.
Bài giải:
Hình vẽ minh họa bài toán:
O
E
B
A
C
Ta có: CO = CE + EO = 36000 + 6400 = 42400km
Xét ∆COA vuông tại A (vì CA là tiếp tuyến của (O) nên CA
¿
OA)
⇒CO
2
=CA
2
+OA
2
(định lí Pytago)
⇒CA
2
= CO
2
− OA
2
= 42400
2
− 6400
2
⇒CA=
√
42400
2
−6400
2
≈41914,2km
Vậy vị trí xa nhất trên Trái Đất có thể nhận tín hiệu của vệ tinh cách vệ tinh
khoảng 41914,2km
Bài 3: Khí cầu là một túi đựng không khí nóng, thường có khối lượng riêng nhỏ hơn
không khí xung quanh và nhờ vào lực đẩy Ác-si-mét có thể bay lên cao. Giả sử có thể
xem khinh khí cầu là một khối cầu và các dây nối sẽ tiếp xúc với khối cầu này. Hãy
tính chiều dài của các dây nối để khoảng cách từ buồng lái đến điểm thấp nhất của khí
cầu là 8m. Biết rằng bán kính của khối cầu này là 10m.
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Bài giải:
Hình vẽ minh họa bài toán:
A
D
C
B
O
Ta có: OB = OC = OD = R = 10m
⇒
OA = AD + DO = 8 + 10 = 18m
Xét ∆ABO vuông tại B (vì AB là tiếp tuyến của (O))
⇒OA
2
=OB
2
+AB
2
(định lí Pytago)
⇒ AB
2
=OA
2
−OB
2
=18
2
−10
2
=224
⇒ AB=
√
224=4
√
14≈15m
Vậy chiều dài của các dây nối thỏa yêu cầu bài toán là 15m.
Bài 4: Người ta muốn xây dựng một cây cầu bắc qua một hồ nước hình tròn có bán
kính 2km. Hãy tính chiều dài của cây cầu để khoảng cách từ cây cầu đến tâm của hồ
nước là 1732m.
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Bài giải:
Hình vẽ minh họa bài toán:
H
B
A
O
Ta có: OA = OB = 2km (gt)
Gọi H là trung điểm của AB, dây AB không qua tâm O
⇒
OH
¿
AB tại H (liên hệ giữa đường kính và dây cung)
⇒
OH = 1732m = 1,732km (gt)
Xét ∆OHA vuông tại H
⇒OA
2
=OH
2
+AH
2
(định lý Pytago)
⇒ AH
2
=OA
2
−OH
2
=2
2
−
(
1,732
)
2
⇒ AH=
√
2
2
−
(
1,732
)
2
≈ 1km
Ta có:
AB=2AH=2.1=2km
(vì H là trung điểm của AB)
Vậy chiều dài của cây cầu là khoảng 2km.
Bài 5: Một bánh xe có dạng hình tròn bán kính 20cm lăn đến bức tường hợp với mặt
đất một góc 60
0
. Hãy tính khoảng cách ngắn nhất từ tâm bánh xe đến góc tường.
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Bài giải:
Khi bánh xe chạm tới bức tường thì không thể di chuyển vào thêm được nữa.
Điều này có nghĩa khoảng cách của tâm bánh xe đến góc tường ngắn nhất là khi
bánh xe tiếp xúc với bức tường và mặt đất.
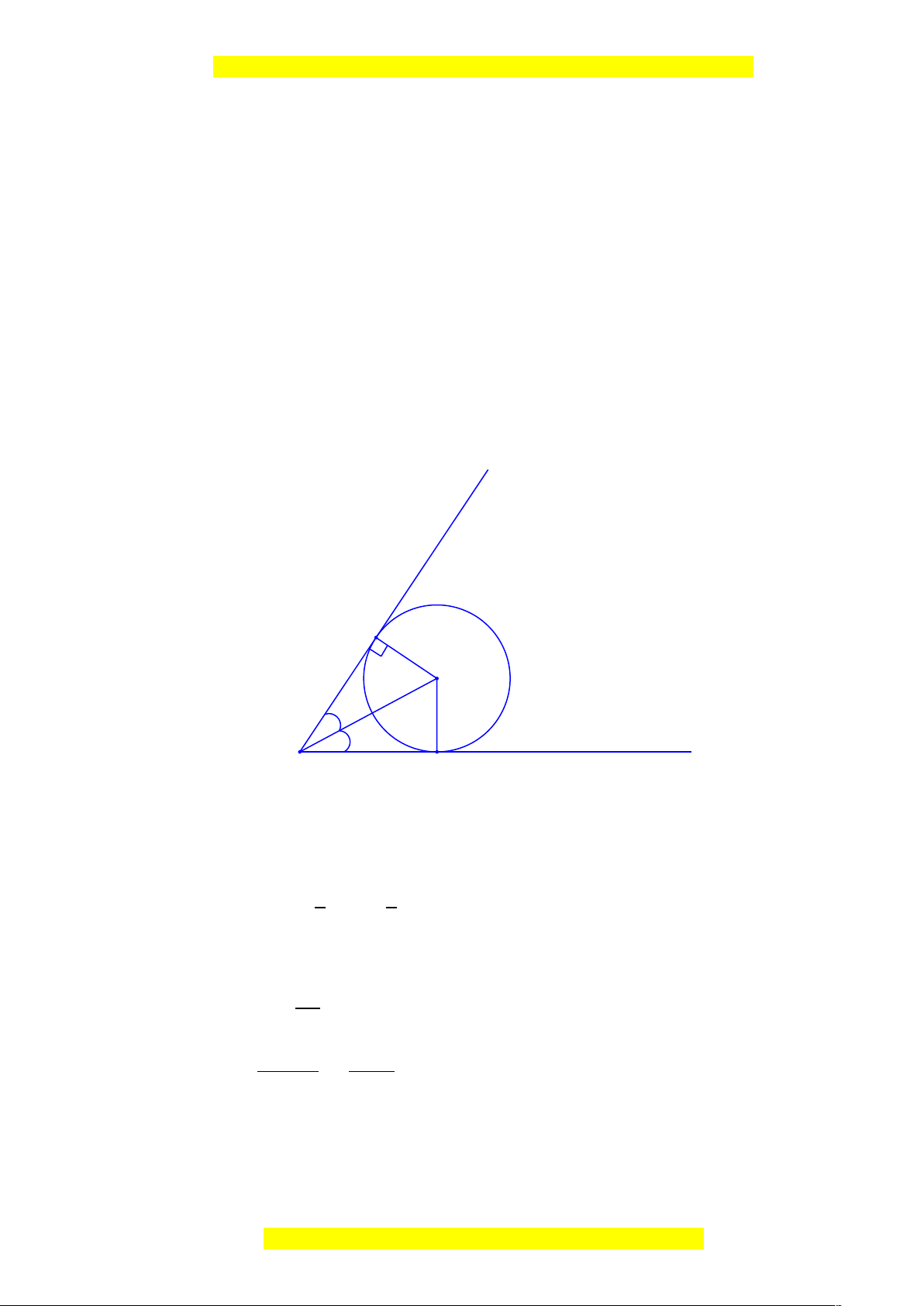
Hình vẽ minh họa bài toán:
30
0
60
0
O
B
C
A
Ta có: OB = OC = 20cm (gt)
B
^
A C=60
0
(gt)
O
^
A B=
1
2
B
^
A C=
1
2
.60
0
= 30
0
(tính chất hai tiếp tuyến cắt nhau)
Xét ∆OAB vuông tại B (vì AB tiếp tuyến của (O) nên AB
¿
OB)
⇒sinB {
^
A O=
OB
OA
¿
(tỉ số lượng giác góc nhọn)
⇒OA=
OB
sinB {
^
A
O=
20
sin30
0
=40cm ¿
Vậy khoảng cách ngắn nhất từ tâm bánh xe đến góc tường là 40cm.
Bài 6: Đường hầm vượt eo biển Măng-sơ nối hai nước Anh và Pháp có chiều dài
khoảng 51km. Giả sử rằng vị trí hai đầu đường hầm thuộc Anh và Pháp nằm trên cùng
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85























