Bộ 39 đề thi giữa kì 1 Toán 10 Kết nối tri thức

700 350 lượt tải
Chia sẻ Facebook Báo cáo tài liệu
Lớp: Lớp 10
Môn: Toán Học
Bộ sách: Kết nối tri thức với cuộc sống
Dạng: Đề thi
File:
Loại: Tài liệu lẻ

CÁCH MUA:

  • B1: Gửi phí vào TK: 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
  • B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án

Liên hệ ngay Hotline hỗ trợ: 084 283 45 85

Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD,  LỜI GIẢI CHI TIẾT và tải về dễ dàng.

Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!

  • Tailieugiaovien.com.vn giới thiệu bộ 39 đề giữa học kì 1 gồm: 10 đề có đầy đủ ma trận và lời giải chi tiết; 29 đề theo các trường Toán 10 Kết nối tri thức mới nhất năm 2023 - 2024 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 10.
  • File word có lời giải chi tiết 100%.
  • Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.

Đánh giá

4.6 / 5(700 )
5
53%
4
22%
3
14%
2
5%
1
7%
Trọng Bình
Tài liệu hay

Giúp ích cho tôi rất nhiều

Duy Trần
Tài liệu chuẩn

Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)

TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học

Xem thêm

TÀI LIỆU BỘ BÁN CHẠY Lớp 10

Xem thêm

Tài liệu bộ mới nhất

TẢI NGAY
Lớp 9 Toán Học

Bộ 5 đề thi Cuối kì 1 Toán 9 Kết nối tri thức (form Hà Nội)

(5.0)

90.000 ₫
5 9
TẢI NGAY
Lớp 10 KTPL

Trắc nghiệm Kinh tế pháp luật 10 Đúng-Sai, Trả lời ngắn (form 2025)

(5.0)

300.000 ₫
15 29
TẢI NGAY
Lớp 9 Toán Học

Đề cương ôn tập Cuối kì 1 Toán 9 Chân trời sáng tạo

(5.0)

80.000 ₫
82 164
TẢI NGAY
Lớp 9 Toán Học

Đề cương ôn tập Cuối kì 1 Toán 9 Cánh diều

(5.0)

80.000 ₫
68 135
TẢI NGAY
Lớp 9 Toán Học

Đề cương ôn tập Cuối kì 1 Toán 9 Kết nối tri thức

(5.0)

80.000 ₫
189 378
TẢI NGAY
Lớp 9 Toán Học

Bộ 5 đề thi Cuối kì 1 Toán 9 Chân trời sáng tạo (form Hà Nội)

(5.0)

90.000 ₫
74 147
TẢI NGAY
Lớp 9 Toán Học

Bộ 5 đề thi Cuối kì 1 Toán 9 Cánh diều (form Hà Nội)

(5.0)

90.000 ₫
35 69
TẢI NGAY
Lớp 9 Toán Học

Bộ 5 đề thi Cuối kì 1 Toán 9 Chân trời sáng tạo có đáp án

(5.0)

90.000 ₫
2.1 K 4.2 K
TẢI NGAY
Lớp 9 Toán Học

Bộ 10 đề thi Cuối kì 1 Toán 9 Cánh diều có đáp án

(5.0)

150.000 ₫
1.2 K 2.3 K
TẢI NGAY
Lớp 9 Toán Học

Bộ 10 đề thi Cuối kì 1 Toán 9 Kết nối tri thức có đáp án

(5.0)

150.000 ₫
3.1 K 6.3 K
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ 1
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 21 câu (70%)
Câu hỏi tự luận: 3 câu (30%)
TT
Nội dung kiến
thức
Đơn vị kiến thức
Mức độ nhận thức
Tổng
%
tổng
điểm
Nhận biết
Thông hiểu
Vận dụng cao
Số CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
Số
CH
Thời
gian
(phút)
TN
TL
1
1. Mệnh đề.
Tập hợp
1.1. Mệnh đề
2
3
1
2
3
59
60
1.2. Tập hợp
2
3
3
7
1
15
5
1
2
2. Bất phương
trình- Hệ bất
phương trình
bậc nhất hai
ẩn.
2.1. Bất phương trình bậc
nhất hai ẩn.
1
1
1
3
2
2.2. Hệ bất phương trình bậc
nhất hai ẩn.
1
2
1
3
1
20
2
1
3
3. Hệ thức
lượng trong
tam giác
3.1. Giá trị lượng giác của
một góc từ 0° đến 180°.
2
3
1
2
3
31
40
3.2. Hệ thức lượng trong
tam giác
1
2
1
3
1
15
2
1
4
4. Vectơ
4.1. Các khái niệm mở đầu
2
2
2
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
4.2. Tổng và hiệu của hai
vectơ
1
2
1
2
2
Tổng
12
18
9
22
2
30
1
20
21
3
90
Tỉ lệ (%)
40
30
10
100
Tỉ lệ chung (%)
70
30
100
Lưu ý:
- Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
- Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.
- Số điểm tính cho 1 câu trắc nghiệm là 1/3 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
BẢNG ĐẶC TẢ ĐỀ KIỂM TRA GIỮA KỲ 1
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút
TT
Nội dung
kiến thức
Đơn vị
kiến thức
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá
Số câu hỏi theo mức độ nhận thức
Nhận
biết
Thông
hiểu
Vận
dụng
Vận dụng
cao
1
1.
1.1.
Mệnh đề
Nhận biết:
- Nhận biết được thế nào là một mệnh đề, mệnh đề phủ định, mệnh đề chứa biến.
2
1
0
0
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
Mệnh đề.
Tập hợp
- Nhận biết được mệnh đề phủ định của mệnh đề chứa kí hiệu với mọi
( )
và kí
hiệu tồn tại
( )
.
- Nhận biết được mệnh đề kéo theo, mệnh đề tương đương.
Thông hiểu:
- Biết lấy ví dụ mệnh đề, phủ định một mệnh đề, xác định được tính đúng sai của
các mệnh đề trong những trường hợp đơn giản.
- Biết lập mệnh đề đảo của một mệnh đề cho trước.
- Phân biệt được điều kiện cần và điều kiện đủ, giả thiết và kết luận.
- Phân biệt được mệnh đề kéo theo và mệnh đề tương đương cho trước.
1.2.
Tập hợp
Nhận biết:
- Nhận biết được
( )
(
) ( ) (
( )
a; b ; a; b ; a; b ; a;b ; ;a ; ;a ; a;− − +
) ( )
a; ; ;+ − +
theo định nghĩa.
- Nhận biết được một phần tử thuộc hay không thuộc một tập hợp cho trước.
- Nhận biết được tập con của tập cho trước.
- Nhận biết được mối quan hệ giữa các tập hợp
; ; ; ;
.
Thông hiểu:
- Xác định được tập hợp con, tập hợp bằng nhau.
2
3
1
0
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
- Xác định được giao của hai tập hợp, hợp của hai tập hợp, hiệu của hai tập hợp,
phần bù của một tập con
Vận dụng:
- Vận dụng được biểu đồ Ven để giải quyết một bài toán thực tế.
- Xác định tham số
m
để hai tập hợp cho trước thỏa điều kiện cho trước.
2
2. Bất
phương
trình- Hệ
bất
phương
trình bậc
nhất hai
ẩn.
2.1. Bất
phương
trình bậc
nhất hai
ẩn.
Nhận biết:
- Nhận biết được bất phương trình bậc nhất hai ẩn.
- Nhận biết được nghiệm của một bất phương trình bậc nhất hai ẩn.
- Biết được biểu diễn hình học của một nghiệm, một tập nghiệm của bất phương
trình bậc nhất hai ẩn trên mặt phẳng tọa độ.
Thông hiểu:
- Xác định được miền nghiệm của một bất phương trình bậc nhất hai ẩn cho trước
hoặc ngược lại.
- Xác định được một điểm cho trước thuộc hay không thuộc miền nghiệm của một
bất phương trình bậc nhất hai ẩn cho trước.
1
1
0
0
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
2.2. Hệ bất
phương
trình bậc
nhất hai
ẩn.
Nhận biết:
- Nhận biết được hệ bất phương trình bậc nhất hai ẩn.
- Nhận biết được nghiệm của một hệ bất phương trình bậc nhất hai ẩn.
- Biết được biểu diễn hình học của một nghiệm, một tập nghiệm của hệ bất phương
trình bậc nhất hai ẩn trên mặt phẳng tọa độ.
Thông hiểu:
- Xác định được miền nghiệm của một hệ bất phương trình bậc nhất hai ẩn cho
trước.
- Xác định được một điểm cho trước thuộc hay không thuộc miền nghiệm của một
hệ bất phương trình bậc nhất hai ẩn cho trước.
Vận dụng
- Tính được số nghiệm nguyên của một hệ bất phương trình bậc nhất hai ẩn cho
trước.
- Lập được hệ bất phương trình bậc nhất hai ẩn từ một bài toán thực tế cho trước.
Vận dụng cao
-Vận dụng được kiến thức đã biết và các kiến thức về hệ bất phương trình bậc nhất
hai ẩn vào giải quyết một bài toán thực tiễn.
1
1
1
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
3
3. Hệ thức
lượng
trong tam
giác
3.1. Giá trị
lượng giác
của một
góc từ 0°
đến 180°.
Nhận biết:
- Nhận biết được dấu của các giá trị lượng giác của một góc nhọn, tù.
- Nắm được mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau.
Thông hiểu:
- Tính (rút gọn) được một biểu thức lượng giác cho trước thông qua việc sử dụng
định nghĩa các giá trị lượng giác và giá trị lượng giác của hai góc bù nhau.
- Xác định được dấu của một biểu thức liên quan đến dấu của các giá trị lượng giác
của một góc thỏa điều kiện cho trước.
Vận dụng
- Vận dụng được kiến thức tổng hợp trong bài để tính giá trị hoặc thu gọn một biểu
thức.
2
1
0
0
3.2. Hệ
thức lượng
trong tam
giác
Nhận biết:
- Nhận biết được tính Đúng/ Sai của các công thức được xây dựng từ các định lí
đã học.
Thông hiểu:
- Tính được cạnh, góc, bán kính đường tròn nội, ngoại tiếp; độ dài đường trung
tuyến, diện tích tam giác từ giả thiết cho trước.
Vận dụng:
- Vận dụng được các định lí đã học vào giải quyết một bài toán thực tiễn.
Vận dụng cao.
1
1
1
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
- Vận dụng các kiến thức đã biết cùng với các nội dung đã học trong bài vào giải
quyết một bài toán thực tế tổng hợp.
4
4. Vectơ
4.1. Các
khái niệm
mở đầu
Nhận biết:
- Nhận biết khái niệm vectơ, vectơ bằng nhau, vectơ – không.
- Biểu diễn các đại lượng trong thực tiễn bằng vectơ.
Thông hiểu:
- Thực hiện các phép tính tổng hiệu vectơ, tích của một vec tơ với một số, tích vô
hướng của hai vec tơ) và mô tả những tính chất hình học (ba điểm thằng hàng,
trung điểm của đoạn thẳng, trọng tâm của tam giác, ...) bằng vectơ.
2
4.2. Tổng
và hiệu
của hai
vectơ
1
1
Tổng
12
9
2
1
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
SỞ GIÁO DỤC VÀ ĐÀO TẠO ...
TRƯỜNG ...
ĐỀ KIỂM TRA GIỮA KÌ I
NĂM HỌC 2022 - 2023
Môn: Toán lớp 10
Thời gian làm bài: 90 phút
(không kể thời gian giao đề)
PHẦN I. TRẮC NGHIỆM (7 điểm)
Câu 1. Trong các câu sau, câu nào là mệnh đề đúng?
A. Làm ơn hãy im lặng!; B. Tháp Eiffel nằm ở Anh;
C. Biển ở Phú Quốc thật đẹp; D.
11
là số nguyên tố.
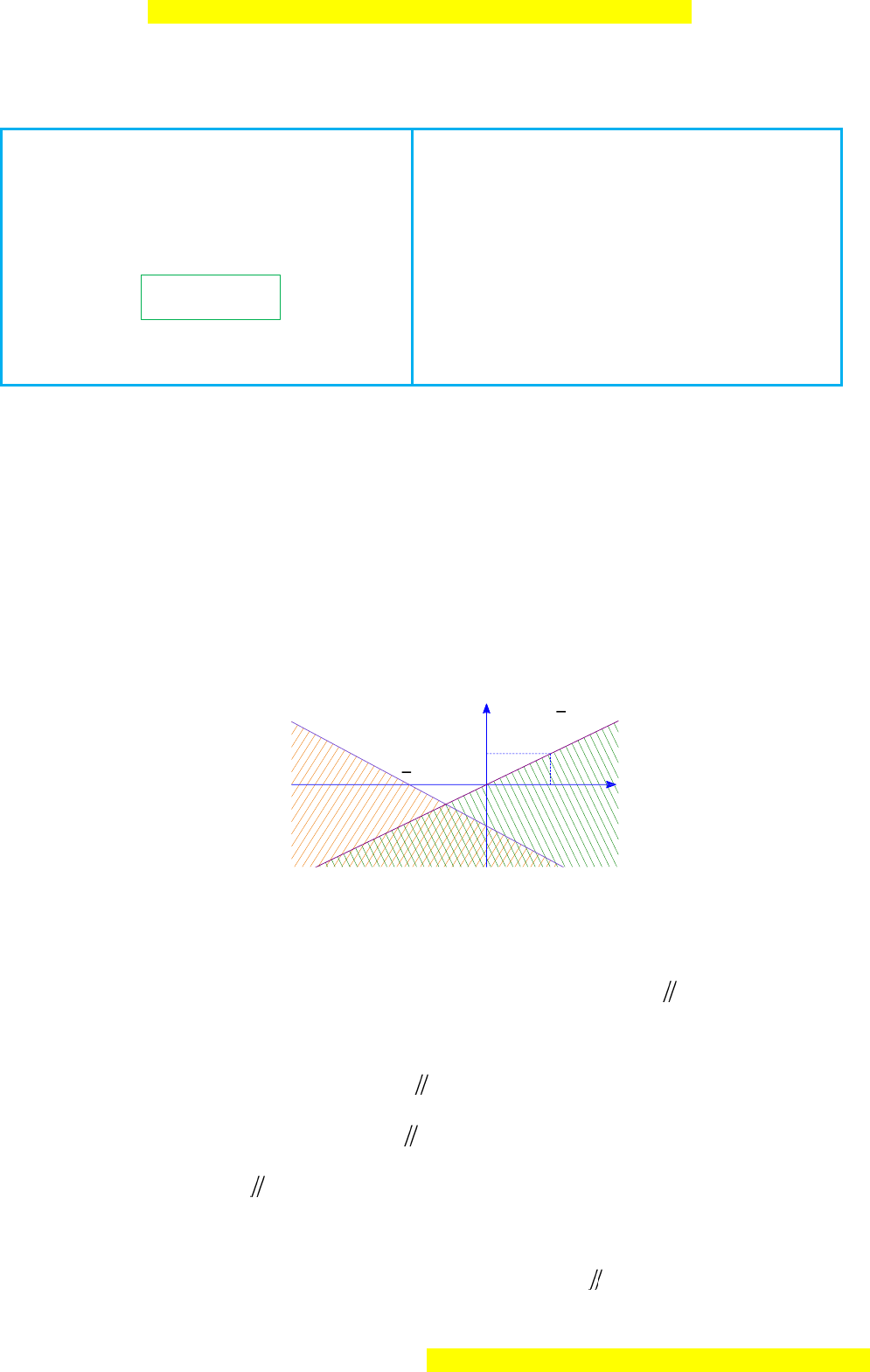
Câu 2. Trong hình vẽ dưới, phần mặt phẳng không bị gạch sọc (kể cả biên) là miền
nghiệm của hệ bất phương trình nào dưới đây?
A.
20
32
−
+ −
xy
xy
; B.
20
32
−
+ −
xy
xy
; C.
20
32
−
+ −
xy
xy
; D.
20
32
−
+ −
xy
xy
.
Câu 3: Cho mệnh đề sau: “Tứ giác
ABCD
là hình bình hành thì
AB CD
”. Phát biểu
nào dưới đây là đúng?
A. Điều kiện cần để tứ giác
ABCD
có
AB CD
là tứ giác
ABCD
là hình bình hành;
B. Điều kiện đủ để tứ giác
ABCD
có
AB CD
là tứ giác
ABCD
là hình bình hành;
C. Tứ giác
ABCD
có
AB CD
là điều kiện cần và đủ để tứ giác
ABCD
là hình bình
hành;
D. Tứ giác
ABCD
là hình bình hành là điều kiện cần để
AB CD
.
x
2
y
=
0
x
+
3
y
+
2
=
0
2
2
1
y
x
O
Đề số: ......
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
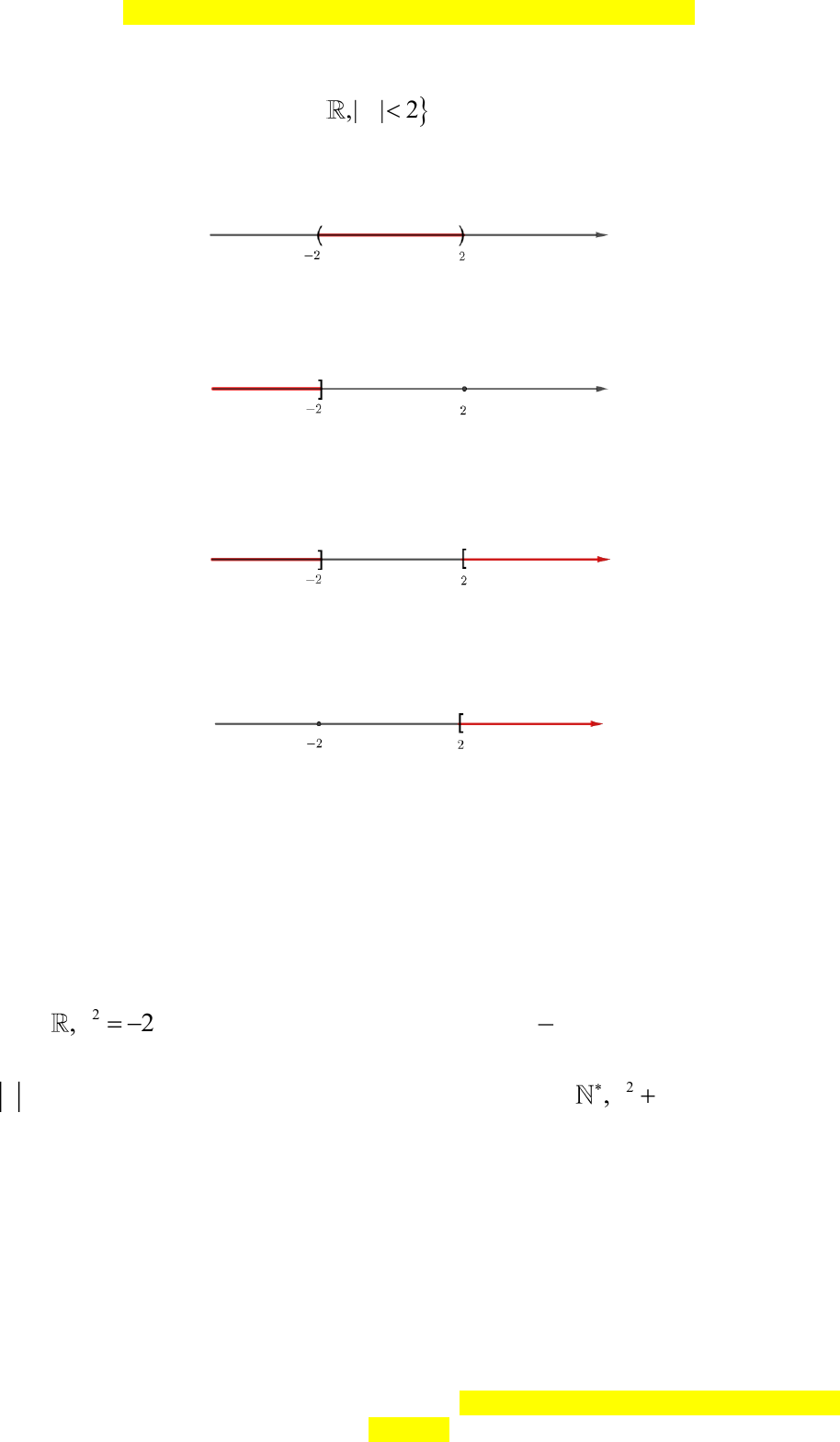
Câu 4. Biểu diễn tập hợp
,| | 2= A x x
trên trục số ta được
A.
B.
C.
D.
Câu 5. Cho tập hợp
1; 0; 3; 5; 7; 9=−A
và
2; 0; 9=−B
. Phần tử thuộc tập
\AB
là
A.
0
; B.
8
; C.
2−
; D.
3
.
Câu 6. Trong các câu sau, mệnh đề nào là mệnh đề chứa biến?
A.
2
,2 = −xx
; B.
1
30
2
− + =x
;
C.
0x
với mọi giá trị thực của x; D.
2
,0
+ x x x
.
Câu 7. Cho hai tập hợp
2; 4; 5; 8;10;17=X
và
1; 3; 5; 8;12;17=Y
. Số phần tử
của tập hợp
XY
là
A. 0; B. 1; C. 2; D. 3.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Câu 8. Trong các cặp số
( )
;xy
sau đây, cặp nào là nghiệm của bất phương trình
21
0
− +
−
xy
xy
?
A.
( )
1; 5
; B.
( )
1; 3−
; C.
( )
0;1
; D.
( )
1;1
.
Câu 9. Cho góc
0 180
thỏa mãn
tan 4=
. Giá trị của biểu thức
sin cos
sin 3cos
+
=
−
A


là
A.
1=A
; B.
1
2
=A
; C.
1
5
=A
; D.
5=A
.
Câu 10. Trong các đẳng thức sau, đẳng thức nào đúng với mọi góc
( )
0 ;180
?
A.
( )
sin 180 sin − =

; B.
( )
sin 180 os − = c

;
C.
( )
sin 180 os − = −c

; D.
( )
sin 180 sin − = −

.
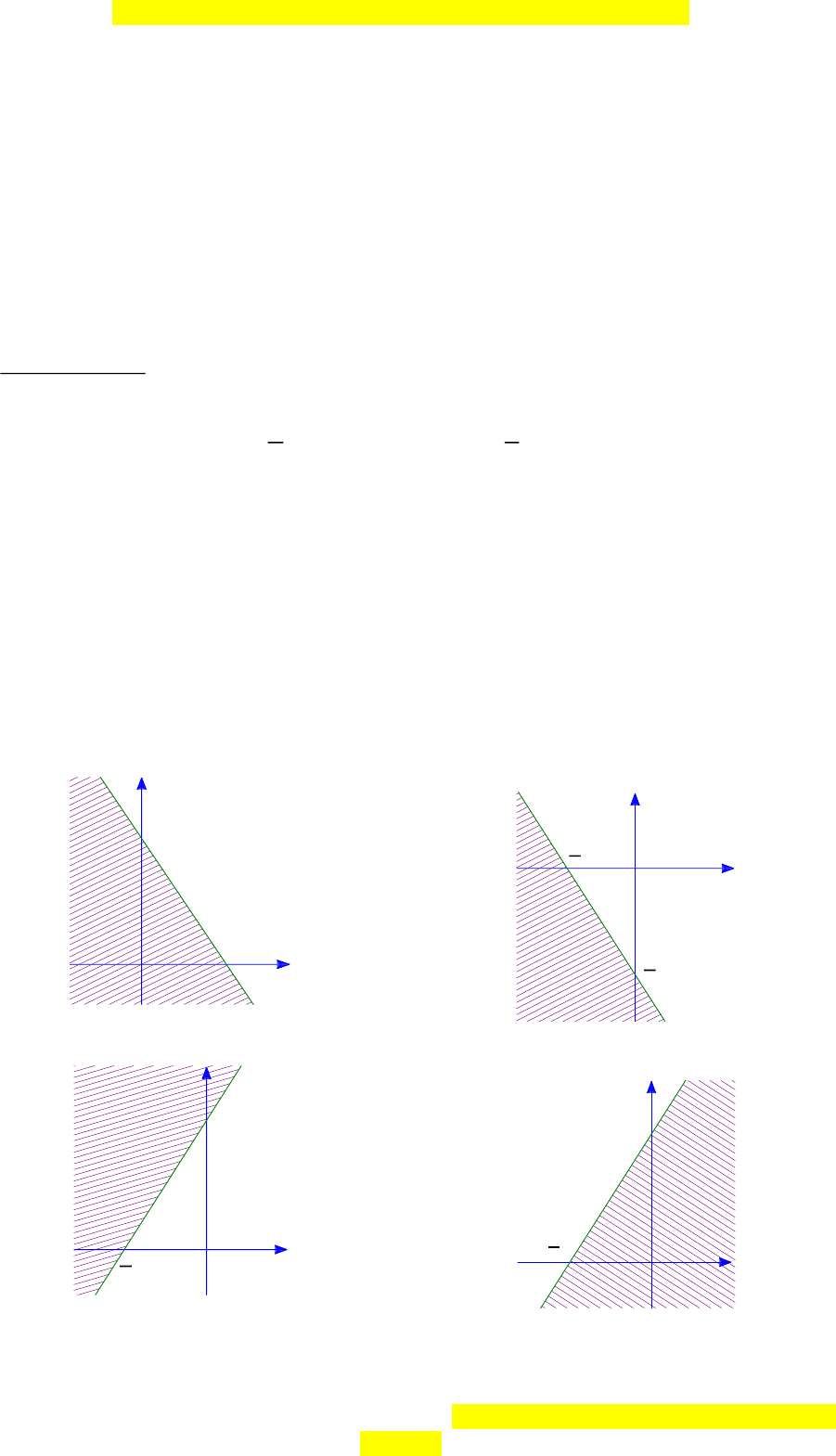
Câu 11. Miền nghiệm của bất phương trình
3 2 6− −xy
được biểu diễn bởi phần
không gạch chéo trong hình nào được cho dưới đây?
A.
B.
C.
D.
d
3
O
2
y
x
d
3
O
2
y
x
d
3
O
2
y
x
d
3
O
2
y
x
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Câu 12. Cho tập hợp
; ;1; 5=M m n
. Số tập con của tập hợp M luôn chứa hai phần
tử m và n là
A.
16
; B.
8
; C.
4
; D.
3
.
Câu 13. Bất phương trình
3+xy
có bao nhiêu nghiệm?
A.
1
; B.
2
; C. Vô nghiệm; D. Vô số nghiệm.
Câu 14. Cho tam giác
ABC
vuông tại
A
. Khẳng định nào sau đây là đúng?
A.
sin 0=A
; B.
( )
sin os=+A c B C
;
C.
( )
sin os= − +A c B C
; D.
( )
sin sin=+A B C
.
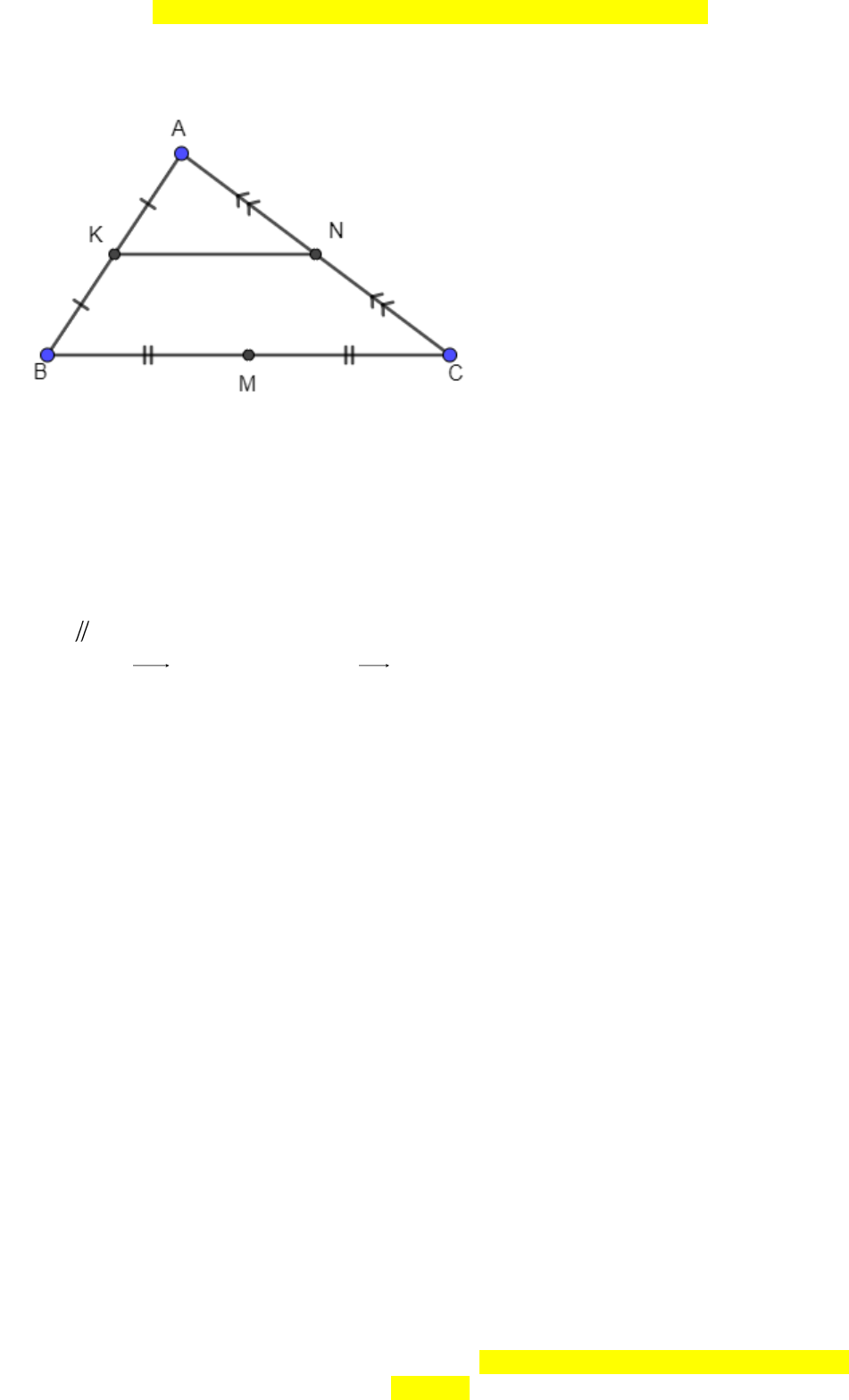
Câu 15. Cho tam giác
ABC
. Điểm
,,K M N
lần lượt là trung điểm của đoạn thẳng
,AB BC
và
AC
. Vectơ nào sau đây cùng phương với
KN
?
A.
CB
; B.
AC
; C.
MN
; D.
BN
.
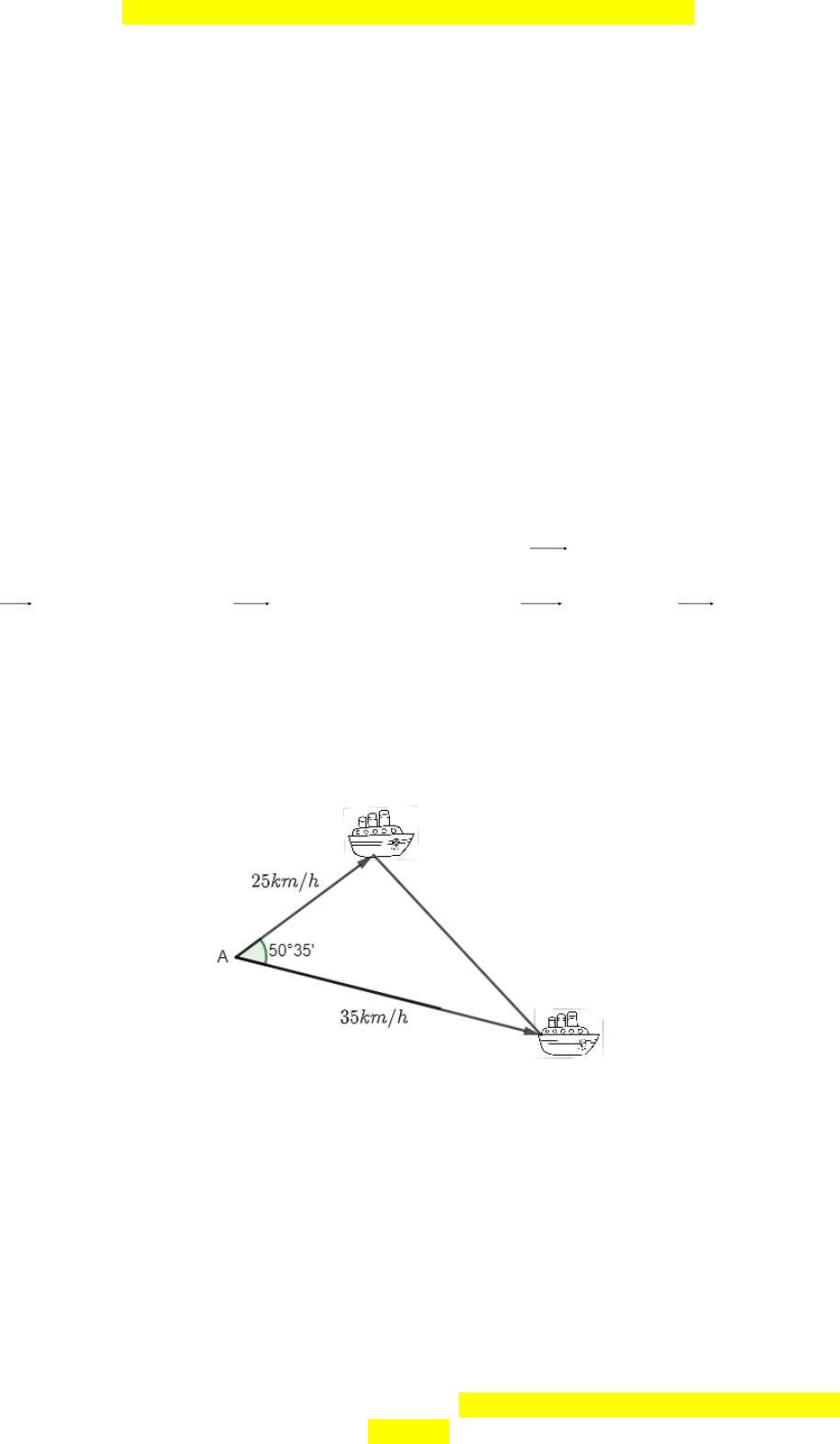
Câu 16. Hai chiếc tàu thủy cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với
nhau một góc
50 35'
. Tàu thứ nhất chạy với tốc độ
25
km/h, tàu thứ hai chạy với tốc
độ
35
km/h. Hỏi sau
1,2
giờ hai tàu cách nhau bao nhiêu km?
A.
27,18
; B.
32,62
; C.
54,36
; D.
63,91
.
Câu 17. Cho tam giác
ABC
có
,Rr
lần lượt là bán kính đường tròn ngoại tiếp, đường
tròn nội tiếp tam giác
ABC
,
S
là diện tích tam giác
ABC
và
p
là nửa chu vi tam giác
ABC
. Công thức tính bán kính ngoại tiếp đường tròn ngoại tiếp tam giác
ABC
nào
sau đây sai?
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
A.
2sin
a
A
; B.
2
sin
b
B
; C.
4
abc
pr
; D.
4
abc
S
.
Câu 18. Cho ba điểm A, B, C. Mệnh đề nào sau đây là đúng?
A.
+=BA CB CA
; B.
+=AB CA BC
;
C.
−=AB AC BC
; D.
+=AB AC BC
.
Câu 19. Khẳng định nào sai trong các khẳng định sau?
A. Vectơ là một đoạn thẳng có hướng;
B. Vectơ – không là vectơ có điểm đầu và điểm cuối trùng nhau;
C. Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài;
D. Hai vectơ cùng phương thì có giá song song với nhau.
Câu 20. Vectơ tổng
+ + + +MN PQ RN NP QR
bằng
A.
MN
; B.
RN
; C.
MR
; D.
NP
.
Câu 21. Phát biểu nào dưới đây là sai?
A.
2 007;2 022 2 007;2 022
; B.

;
C.
)
0; +
; D.
2; 6 2;3;4;5;6=
.
II. TỰ LUẬN (3 ĐIỂM)
Bài 1. (1,0 điểm)
Cho tập hợp
| 1 4= − A x x
.
a) Xác định phần bù của tập A trong tập hợp số thực.
b) Cho tập hợp
10; 2= − −Bm
. Tìm m để
AB
.
Bài 2 (1,0 điểm) Thời gian (tính bằng giờ) cần thiết để lắp ráp và đóng gói hai loại sản
phẩm A và B được thể hiện trong bảng dưới đây.
Quy trình
Sản phẩm A
Sản phẩm B
Lắp ráp
3
3
Đóng gói
1
2
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Tổng số thời gian để lắp ráp và đóng gói sản phẩm lần lượt không quá 360 giờ, 200
giờ. Lợi nhuận khi bán sản phẩm A là 2 triệu đồng, sản phẩm B là 3 triệu đồng. Cần
sản xuất bao nhiêu sản phẩm mỗi loại để lợi nhuận thu được là lớn nhất.
Bài 3: (1,0 điểm) Cho tam giác
ABC
có
120=A
và
==AB AC a
. Trên cạnh
BC
lấy điểm
M
sao cho
2
5
=
BC
BM
. Tính độ dài
AM
và bán kính đường tròn nội tiếp
tam giác
ABM
.
-------------------------------- Hết -------------------------------
(Cán bộ coi thi không giải thích gì thêm)
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
PHẦN I. TRẮC NGHIỆM (7 điểm)
BẢNG ĐÁP ÁN
1. D
2. A
3. B
4. A
5. D
6. B
7. D
8. D
9. D
10. A
11. C
12. C
13. D
14. D
15. A
16. B
17. B
18. A
19. D
20. A
21. D
LỜI GIẢI CHI TIẾT
Câu 1.
Hướng dẫn giải
Đáp án đúng là: D
Câu “Làm ơn hãy im lặng!” là một câu cảm thán nên không phải mệnh đề. Do đó A
sai.
Câu “Tháp Eiffel nằm ở Anh” là một câu khẳng định sai nên là mệnh đề sai. Do đó B
sai.
Câu “Biển ở Phú Quốc thật đẹp” là một câu khẳng định nhưng chưa thể khẳng định
được tính đúng sai nên không là mệnh đề. Do đó C sai.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Câu “
11
là số nguyên tố” là một câu khẳng định đúng nên là mệnh đề đúng. Do đó D
đúng.
Câu 2.
Hướng dẫn giải
Đáp án đúng là: A
Lấy điểm (0; 1) thuộc vào miền nghiệm của hệ bất phương trình cần tìm.
Xét đường thẳng d
1
:
3 2 0 3 2+ + = + = −x y x y
Tại điểm (0; 1) có:
0 3.1 3 2+ = −
, miền nghiệm D
1
của bất phương trình có bờ là
đường thẳng d
1
là nửa mặt phẳng chứa điểm (0; 1) và kể biên nên biểu diễn cho bất
phương trình
32+ −xy
. (1)
Xét đường thẳng d
2
:
20−=xy
Tại điểm (0; 1) có:
0 2.1 2 0− = −
, miền nghiệm D
2
của bất phương trình có bờ là
đường thẳng d
2
là nửa mặt phẳng chứa điểm (0; 1) và kể biên nên biểu diễn cho bất
phương trình
20−xy
. (2)
Từ (1) và (2) ta có hệ bất phương trình cần tìm là:
32
20
+ −
−
xy
xy
.
Câu 3:
Hướng dẫn giải
Đáp án đúng là: B
Ta có:
Điều kiện đủ để tứ giác
ABCD
có
AB CD
là tứ giác
ABCD
là hình bình hành.
Điều kiện cần để tứ giác
ABCD
là hình bình hành là tứ giác
ABCD
có
AB CD
.
Do đó A sai, D sai và B đúng.
Vì tứ giác
ABCD
có
AB CD
chưa đủ điều kiện để khẳng định tứ giác
ABCD
là
hình bình hành nên đáp án C sai.
Câu 4.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Hướng dẫn giải
Đáp án đúng là: A
Ta có:
2 2 2 − xx
.
Khi đó
,| | 2 , 2 2 ( 2; 2)= = − = −A x x x x
.
Biểu diễn tập hợp A trên trục số ta được:
Câu 5.
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
\ 1; 2; 3; 5; 7=−AB
.
Khi đó:
0 ∉ A\B. Do đó A sai.
8 ∉ A\B. Do đó B sai.
– 2 ∉ A\B. Do đó C sai.
3 ∈ A\B. Do đó D đúng.
Câu 6.
Hướng dẫn giải
Đáp án đúng là: B
+) Câu “∃x ∈ ℝ, x
2
= – 2”: là một khẳng định sai vì không có giá trị của x nào thỏa
mãn x
2
= – 2. Do đó câu A là một mệnh đề.
+) Câu “
1
2
−
x + 3 = 0”: có tính đúng sai phụ thuộc vào giá trị của x nên câu này là một
mệnh đề chứa biến.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
+) Câu “|x| ≥ 0 với mọi giá trị thực của x”: là một khẳng định đúng vì giá trị tuyệt đối
của một số thực luôn luôn không âm. Do đó câu này là một mệnh đề.
+) Câu “∀x ∈ ℕ*, x
2
+ x > 0”: là một khẳng định đúng vì với số tự nhiên x khác 0 thì
x
2
+ x luôn dương. Do đó câu này là một mệnh đề.
Câu 7.
Hướng dẫn giải
Đáp án đúng là: D
Ta có:
5; 8;17=XY
.
Vậy số phần tử của tập
XY
là
3
.
Câu 8.
Hướng dẫn giải
Đáp án đúng là: D
+) Thay
1=x
và
5=y
vào từng bất phương trình của hệ đã cho ta được:
2.1 5 1 3 1− +
là một mệnh đề sai.
1 5 0 4 0− −
là một mệnh đề sai.
Do đó cặp
( )
1; 5
không là nghiệm của hệ bất phương trình đã cho.
+) Thay
1=−x
và
3=y
vào từng bất phương trình của hệ đã cho ta được:
( )
2. 1 3 1 5 1− − +
là một mệnh đề sai.
1 3 0 4 0− − −
là một mệnh đề sai.
Do đó cặp
( )
1; 3−
không là nghiệm của hệ bất phương trình đã cho.
+) Thay
0=x
và
1=y
vào từng bất phương trình của hệ đã cho ta được:
2.0 1 1 1 1− +
là một mệnh đề sai.
0 1 0 1 0− −
là một mệnh đề sai.
Do đó cặp
( )
0;1
không là nghiệm của hệ bất phương trình đã cho.
+) Thay
1=x
và
1=y
vào từng bất phương trình của hệ đã cho ta được:
2.1 1 1 1 1− + −
là một mệnh đề đúng.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
1 1 0 0 0−
là một mệnh đề đúng.
Do đó cặp
( )
1;1
là nghiệm của bất phương trình đã cho.
Vậy chọn đáp án D.
Câu 9.
Hướng dẫn giải
Đáp án đúng là: D
Xét biểu thức
sin cos
sin 3cos
+
=
−
A


Ta có
tan 4=
nên
0cos
.
Chia cả tử và mẫu của biểu thức A cho
0cos
, ta được:
sin cos
tan 1
cos cos
sin cos
tan 3
3
cos cos
+
+
==
−
−
A




.
Thay
tan 4=
vào biểu thức trên ta được
4 1 5
5
4 3 1
+
= = =
−
A
.
Vậy giá trị biểu thức A là 5 khi
tan 4=
.
Câu 10.
Hướng dẫn giải
Đáp án đúng là: A
Với
( )
0 ;180
thì
( )
sin 180 sin − =

.
Câu 11.
Hướng dẫn giải
Đáp án đúng là: C
Xét đường thẳng
3 2 6− = −xy
Chọn
03= =xy
Chọn
02= = −yx
Suy ra đường thẳng
3 2 6− = −xy
đi qua hai điểm có tọa độ (0; 3) và (– 2; 0).
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Lấy O(0; 0) có 3.0 – 2.0 = 0 > 0 – 6 nên điểm O thuộc miền nghiệm của bất phương
trình đã cho do đó miền nghiệm là nửa mặt phẳng bờ là đường thẳng
3 2 6− = −xy
chứa điểm O và không kể đường thẳng.
Vì vậy hình vẽ C là hình biểu diễn miền nghiệm của bất phương trình đã cho.
Câu 12.
Hướng dẫn giải
Đáp án đúng là: C
Ta có:
Tập con có
2
phần tử:
;mn
;
Tập con có
3
phần tử:
; ;1 , ; ; 5m n m n
.
Tập con có
4
phần tử:
; ;1; 5mn
.
Vậy có
4
tập con của
M
thỏa mãn yêu cầu.
Câu 13.
Hướng dẫn giải
Đáp án đúng là: D
Bất phương trình
3+xy
có vô số nghiệm.
Câu 14.
Hướng dẫn giải
Đáp án đúng là: D
Xét tam giác ABC, có:
90=A
nên
sin 1=A
( )
180 180+ + = = − +A B C A B C
(tổng 3 góc trong tam giác)
Do đó
( )
( )
( )
sin sin 180 sin= − + = +A B C B C
.
Câu 15.
Hướng dẫn giải
Đáp án đúng là: A
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Xét tam giác
ABC
, có:
K
là trung điểm
AB
,
N
là trung điểm
AC
Suy ra
KN
là đường trung bình của tam giác
ABC
KN BC
Do đó vectơ
KN
cùng phương với
CB
.
Câu 16.
Hướng dẫn giải
Đáp án đúng là: B
Giả sử sau
1,2
giờ thì tàu thứ nhất đến vị trí
B
, tàu thứ hai đến được vị trí
C
.
Sau
1,2
giờ:
Tàu thứ nhất đi được quãng đường
AB
dài:
( )
25 .1,2 30= km
.
Tàu thứ hai đi được quãng đường
AC
dài:
( )
35 .1,2 42= km
.
Xét tam giác ABC:
Áp dụng định lí cos trong tam giác ABC, ta được:
2 2 2
2. . .cos= + −BC AB AC AB AC A
( )
2 2 2
30 42 2.30.42.cos 50 35' = + − BC
2
1063,91BC
32,62BC
.
Vậy sau 1,2 giờ thì khoảng cách giữa hai tàu khoảng
32,62 km
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Câu 17. Cho tam giác
ABC
có
,Rr
lần lượt là bán kính đường tròn ngoại tiếp, đường
tròn nội tiếp tam giác
ABC
,
S
là diện tích tam giác
ABC
và
p
là nửa chu vi tam giác
ABC
. Công thức tính bán kính ngoại tiếp đường tròn ngoại tiếp tam giác
ABC
nào
sau đây sai?
A.
2sin
a
A
; B.
2
sin
b
B
; C.
4
abc
pr
; D.
4
abc
S
.
Hướng dẫn giải
Đáp án đúng là: B
Xét tam giác
ABC
, có:
Áp dụng định lí sin trong tam giác
ABC
, ta được:
2
sin sin sin 2sin 2sin 2sin
= = = = = =
a b c a b c
RR
A B C A B C
.
Do đó A đúng, B sai.
Diện tích tam giác ABC là:
4 4 4
= = = =
abc abc abc
S pr R
R S pr
.
Do đó C và D đúng.
Câu 18.
Hướng dẫn giải
Đáp án đúng là: A
Áp dụng quy tắc ba điểm, ta có:
+ = + =BA CB CB BA CA
. Do đó A đúng.
+ = + = AB CA CA AB CB BC
. Do đó B sai.
Áp dụng quy tắc hiệu hai vectơ:
− = AB AC CB BC
. Do đó C sai.
Áp dụng quy tắc hình bình hành:
+ = AB AC AD BC
(với D là điểm thỏa mãn ABDC là hình bình hành). Do đó D sai.
Câu 19.
Hướng dẫn giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Đáp án đúng là: D
Hai vectơ cùng phương thì có giá song song hoặc trùng nhau.
Câu 20.
Hướng dẫn giải
Đáp án đúng là A
Ta có:
+ + + +MN PQ RN NP QR
( ) ( )
= + + + +MN NP PQ QR RN
= + +MP PR RN
=+MR RN
= MN
.
Câu 21.
Hướng dẫn giải
Đáp án đúng là: D
+) Ta có:
2 007;2 022 ,2 007 2 022= xx
.
2 007 2 007;2 022
và
2 022 2 007;2 022
Vì vậy
2 007;2 022 2 007;2 022
. Do đó A đúng.
+) Tập
là tập con của mọi tập hợp nên

. Do đó B đúng.
+) Ta có:
0;1;2;3;4;...=
)
0; , 0+ = xx
Vì vậy
)
0; +
. Do đó C đúng.
+) Ta có:
2; 6 ,2 6= xx
2; 3; 4; 6 5; 6 2;
2;3;4;5;6 2; 6
Ta lại có
5
2;6
2
nhưng
5
2;3;4;5;6
2
.
2; 6 2;3;4;5;6
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
Vì vậy
2;3;4;5;6 2; 6
. Do đó D sai.
II. PHẦN TỰ LUẬN (3 ĐIỂM)
Bài 1.
Hướng dẫn giải
a) Ta có:
(
| 1 4 1;4= − = −A x x
.
Khi đó, ta có:
Vì vậy
(
( )
\ ; 1 4;= − − +A
.
b) Để
AB
thì m – 2 > – 1 ⇔ m > 1.
Vậy m > 1 thì
AB
.
Bài 2.
Hướng dẫn giải
Gọi số sản phẩm A là
x
(sản phẩm) và số sản phẩm B là
y
(sản phẩm)
( )
,0xy
.
Tổng thời gian lắp ráp
x
sản phẩm A và
y
sản phẩm B là:
33+xy
(giờ).
Vì thời gian để lắp ráp không quá
360
giờ nên ta có:
3 3 360+xy
hay
120+xy
.
Tổng thời gian đóng gói
x
sản phẩm A và
y
sản phẩm B là:
2+xy
(giờ).
Vì thời gian để lắp ráp không quá 200 giờ nên ta có:
2 200+xy
.
Khi đó ta có hệ bất phương trình:
0
0
120
2 200
+
+
x
y
xy
xy
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
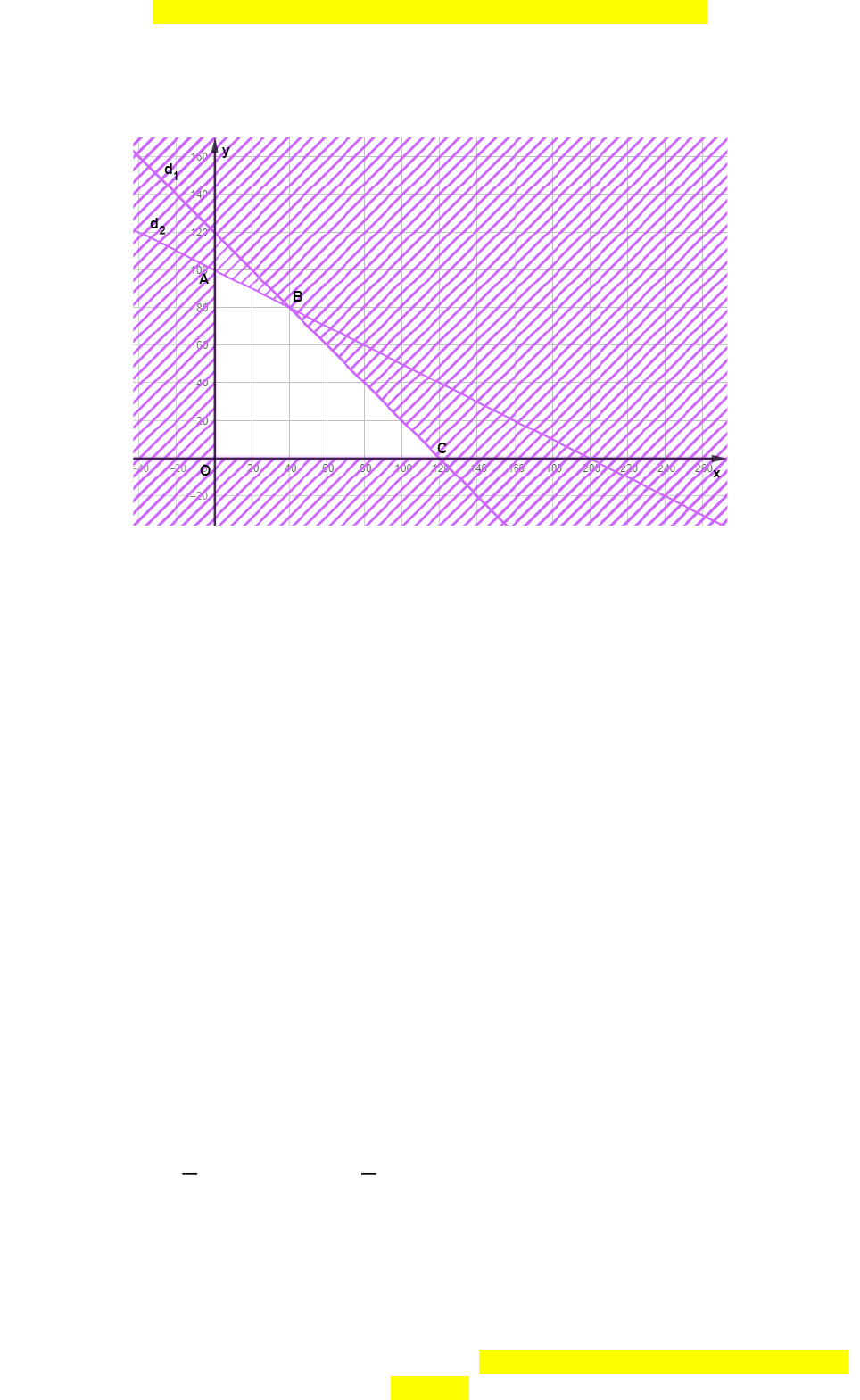
Biểu diễn miền nghiệm với
1
: 120+=d x y
và
2
: 2 200+=d x y
, ta được:
Miền nghiệm của hệ bất phương trình là miền trong của tứ giác OABC với O(0; 0),
A(0; 100), B(40; 80), C(120; 0).
Goi F(x; y) là lợi nhuận thu được khi bán x sản phẩm A và y sản phẩm B.
Khi đó
( )
; 2 3=+F x y x y
Tại O(0; 0), có
( )
0;0 2.0 3.0 0= + =F
.
Tại A(0; 100), có:
( )
0;100 2.0 3.100 300= + =F
.
Tại B(40; 80), có:
( )
40;80 2.40 3.80 320= + =F
.
Tại C(120; 0), có:
( )
120;0 2.120 3.0 240= + =F
.
Vậy để thu được lợi nhuận lớn nhất là 320 triệu đồng thì cần sản xuất 40 sản phẩm A
và 80 sản phẩm B.
Bài 3.
Hướng dẫn giải
+) Xét tam giác ABC, có AB = AC = a nên tam giác ABC cân tại A
( )
( )
11
180 180 120 30
22
= = − = − = ABC ACB BAC
.
Áp dụng định lí cosin trong tam giác ABC, ta được:
2 2 2
2. . . os= + −BC AB AC AB AC c BAC
2 2 2
2. . . os120 = + − BC a a a a c
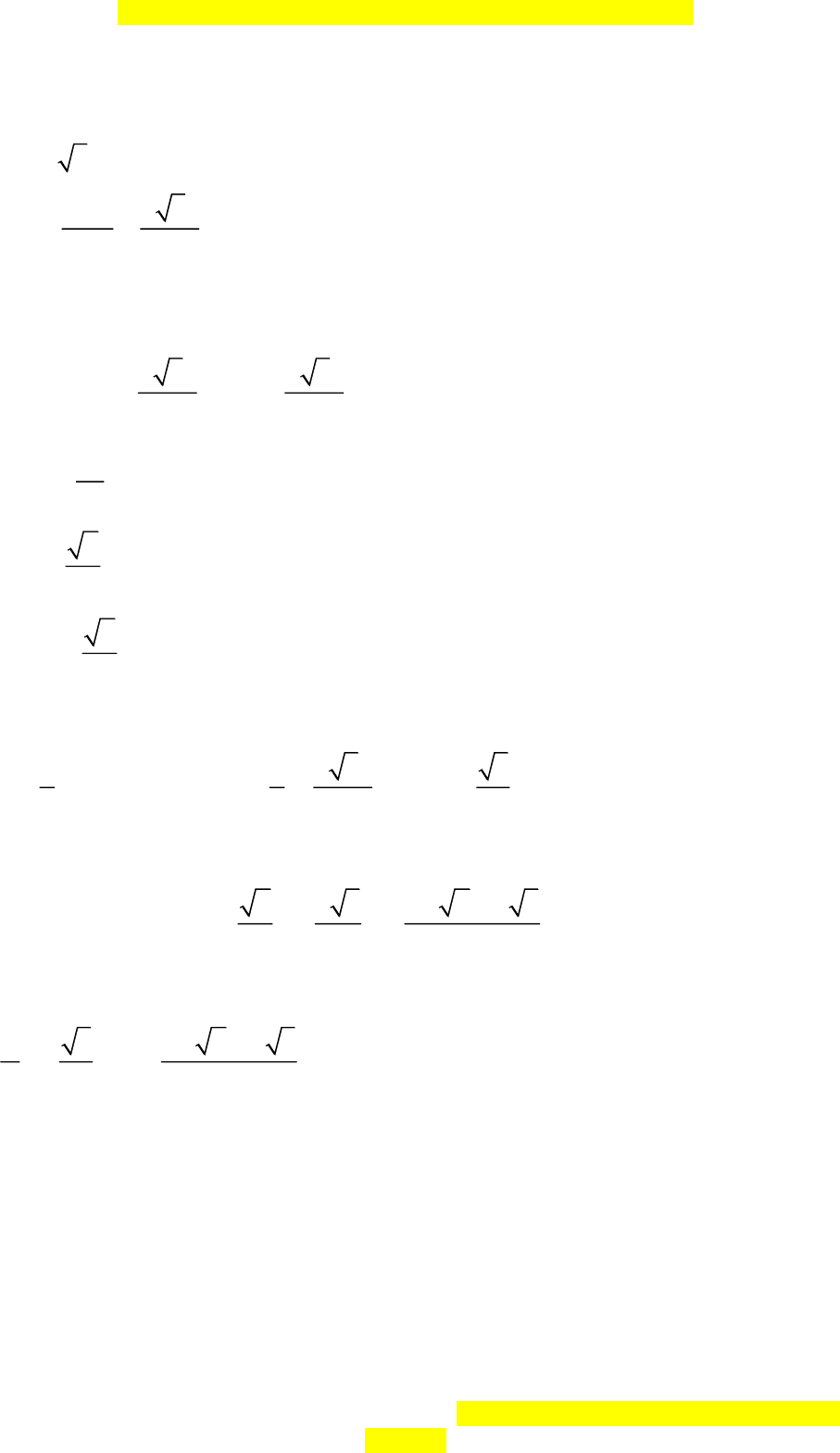
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc xin vui lòng liên hệ hotline: 084
283 45 85
22
3=BC a
3=BC a
2 2 3
55
= =
BC a
BM
.
Áp dụng định lí cosin trong tam giác ABM, ta được:
2 2 2
2. . . os= + −AM AB BM AB BM c ABM
2
22
2 3 2 3
2. . . os30
55

= + −


aa
AM a a c
22
7
25
=AM a
7
5
=AM a
.
Vậy
7
5
=AM a
.
+) Diện tích tam giác
ABM
là:
1 1 2 3 3
. . .sin . . .sin30
2 2 5 10
= = =
ABM
a
S AB BM ABM a
(đvdt).
Chu vi tam giác
ABM
là:
7 2 3 1 7 2 3
5 5 5
++
= + + = + + =p AB AM BM a a a a
(đvđd).
Bán kính đường tròn nội tiếp tam giác ABC là:
2
3 1 7 2 3
: 0,12
10 5
++
= =
S
r a a a
p
.
Vậy bán kính đường tròn nội tiếp tam giác
ABC
là
0,12a
.

Mô tả nội dung:



MA TRẬN ĐỀ KIỂM TRA GIỮA KỲ 1
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
Câu hỏi trắc nghiệm: 21 câu (70%)
Câu hỏi tự luận: 3 câu (30%)
Mức độ nhận thức Tổng % Nhận biết Thông hiểu Vận dụng Vận dụng cao Số CH Nội dung kiến TT
Đơn vị kiến thức Thời tổng thức Thời Thời Thời Thời gian Số Số Số Số điểm gian gian gian gian TN TL (phút) CH CH CH CH (phút) (phút) (phút) (phút) 1. Mệnh đề. 1.1. Mệnh đề 2 3 1 2 3 1 Tập hợp 1.2. Tập hợp 2 3 3 7 1 15 5 1 2. Bất phương
2.1. Bất phương trình bậc 59 60 trình- Hệ bất 1 1 1 3 2 nhất hai ẩn. 2 phương trình bậc nhất hai ẩn.
2.2. Hệ bất phương trình bậc 1 2 1 3 1 20 2 1 nhất hai ẩn.
3.1. Giá trị lượng giác của 3. Hệ thức 2 3 1 2 3
một góc từ 0° đến 180°. 3 lượng trong tam giác
3.2. Hệ thức lượng trong 31 40 1 2 1 3 1 15 2 1 tam giác 4 4. Vectơ
4.1. Các khái niệm mở đầu 2 2 2
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

4.2. Tổng và hiệu của hai 1 2 1 2 2 vectơ Tổng 12 18 9 22 2 30 1 20 21 3 90 Tỉ lệ (%) 40 30 20 10 100 Tỉ lệ chung (%) 70 30 100 Lưu ý:
- Các câu hỏi ở cấp độ nhận biết và thông hiểu là các câu hỏi trắc nghiệm khách quan 4 lựa chọn, trong đó có duy nhất 1 lựa chọn đúng.
- Các câu hỏi ở cấp độ vận dụng và vận dụng cao là các câu hỏi tự luận.
- Số điểm tính cho 1 câu trắc nghiệm là 1/3 điểm/câu; số điểm của câu tự luận được quy định trong hướng dẫn chấm nhưng phải tương ứng với tỉ lệ
điểm được quy định trong ma trận.
BẢNG ĐẶC TẢ ĐỀ KIỂM TRA GIỮA KỲ 1
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút
Số câu hỏi theo mức độ nhận thức Nội dung Đơn vị TT
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Nhận Thông Vận Vận dụng kiến thức kiến thức biết hiểu dụng cao 1.1. Nhận biết: 1 1. 2 1 0 0 Mệnh đề
- Nhận biết được thế nào là một mệnh đề, mệnh đề phủ định, mệnh đề chứa biến.
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85
Mệnh đề.
- Nhận biết được mệnh đề phủ định của mệnh đề chứa kí hiệu với mọi () và kí Tập hợp hiệu tồn tại () .
- Nhận biết được mệnh đề kéo theo, mệnh đề tương đương. Thông hiểu:
- Biết lấy ví dụ mệnh đề, phủ định một mệnh đề, xác định được tính đúng sai của
các mệnh đề trong những trường hợp đơn giản.
- Biết lập mệnh đề đảo của một mệnh đề cho trước.
- Phân biệt được điều kiện cần và điều kiện đủ, giả thiết và kết luận.
- Phân biệt được mệnh đề kéo theo và mệnh đề tương đương cho trước. Nhận biết:
- Nhận biết được (a; b); a; b; (a; b; a;b); (− ;  a ); (− ;  a; (a;+) a;+); ( ;
− +) theo định nghĩa. 1.2.
- Nhận biết được một phần tử thuộc hay không thuộc một tập hợp cho trước. 2 3 1 0 Tập hợp
- Nhận biết được tập con của tập cho trước. 
- Nhận biết được mối quan hệ giữa các tập hợp ; ; ; ; . Thông hiểu:
- Xác định được tập hợp con, tập hợp bằng nhau.
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

- Xác định được giao của hai tập hợp, hợp của hai tập hợp, hiệu của hai tập hợp,
phần bù của một tập con Vận dụng:
- Vận dụng được biểu đồ Ven để giải quyết một bài toán thực tế.
- Xác định tham số m để hai tập hợp cho trước thỏa điều kiện cho trước. Nhận biết: 2. Bất
- Nhận biết được bất phương trình bậc nhất hai ẩn. phương
- Nhận biết được nghiệm của một bất phương trình bậc nhất hai ẩn. 2.1. Bất trình- Hệ phương
- Biết được biểu diễn hình học của một nghiệm, một tập nghiệm của bất phương bất
trình bậc nhất hai ẩn trên mặt phẳng tọa độ. 2 trình bậc 1 1 0 0 phương nhất hai Thông hiểu:
trình bậc ẩn. nhất hai
- Xác định được miền nghiệm của một bất phương trình bậc nhất hai ẩn cho trước ẩn. hoặc ngược lại.
- Xác định được một điểm cho trước thuộc hay không thuộc miền nghiệm của một
bất phương trình bậc nhất hai ẩn cho trước.
Mọi thắc mắc xin vui lòng liên hệ hotline: 084 283 45 85

zalo Nhắn tin Zalo