ƠNG
VI HÀM SỐ VÀ ĐỒ THỊ CHƯ BÀI 15. HÀM SỐ
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM. III ==
DẠNG 1. TẬP XÁC ĐỊNH CỦA HÀM SỐ Câu 1:
Tập xác định của hàm số 4 2
y = x − 2018x − 2019 là A. ( 1 − ;+ ). B. ( ;0 − ). C. (0; + ). D. (− ; + ) . Lời giải Chọn D
Hàm số là hàm đa thức nên xác định với mọi số thực x . Câu 2:
Trong các hàm số sau, hàm số nào có tập xác định là ? 2 x + 2 2x + 3 x + 2 A. 3 2
y = x + 3x −1. B. y = . C. y = . D. y = . x 2 x x −1 Lời giải Chọn A Hàm số 3 2
y = x + 3x −1 là hàm đa thức bậc ba nên tập xác định là . x +1 Câu 3:
Tập xác định của hàm số y = x−1 là: A. . 1; + B. . C. . D. ( ). Lời giải Chọn C
Điều kiện xác định: x −1 0 x 1 x +1
Vậy tập xác định của hàm số y = là D = \ 1 x −1 x − 3 Câu 4:
Tập xác định của hàm số y = là 2x − 2 A. \ 1 . B. \ 3 . C. \ 2 . D. (1; +) .
Lời giải Chọn A
Điều kiện xác định : 2x − 2 0 x 1
Nên tập xác định của hàm số là : D = \ 1 . x + 2 Câu 5:
Tập xác định của hàm số y = ( là x − 3)2 A. ( ;3 − ) . B. (3; + ) . C. \ 3 . D. . Lời giải Chọn C
Điều kiện: x − 3 0 x 3. TXĐ: \ 3 . 3x −1 Câu 6:
Tập xác định D của hàm số y = là 2x − 2 A. D = .
B. D = 1;+) .
C. D = (1; +) .
D. D = R \ 1 . Lời giải Chọn D 3x −1 Hàm số y =
xác định khi x 1 . Vậy D = R \ 1 . 2x − 2 5 Câu 7:
Tập xác định của hàm số y = là 2 x −1 A. \ 1 − . B. \ 1 − ; 1 . C. \ 1 . D. . Lời giải Chọn B x 1
Hàm số đã cho xác định khi 2 x −1 0 . x 1 −
Vậy tập xác định của hàm số là D = \ 1 − ; 1 . x + 5 x −1 Câu 8:
Tập xác định của hàm số f (x) = + là x −1 x + 5 A. D = . B. D = \ 1 { }. C. D = \ { 5 − . } D. D = \ { 5 − ; 1 . } Lời giải Chọn D x −1 0 x 1 Điều kiện: . x + 5 0 x 5 −
Vậy tập xác định của hàm số là: D = \ 1;− 5 . 3 − x Câu 9:
Tập xác định của hàm số y = là 2 x − 5x − 6 A. D = \ 1 − ; 6 B. D = \ 1;− 6 C. D = 1 − ; 6
D. D = 1; − 6 Lời giải Chọn A x − Điều kiện 2 1
x − 5x − 6 0 . x 6 Vậy D = \ 1 − ; 6 . x +1
Câu 10: Tìm tập xác định D của hàm số y = ( . x + ) 1 ( 2 x − 4) A. D = \ 2 B. D = \ 2 C. D = \ 1 − ; 2 D. D = \ 1 − ; 2 Lời giải Chọn D + − Điề x 1 0 x 1 u kiện xác định: . Vậy D = \ 1 − ; 2 . 2 x − 4 0 x 2 Lưu ý: 1 Nếu rút gọn y =
rồi khẳng định D = \
2 là sai. Vì với x = 1 − thì biểu thức 2 x − 4 + ban đầ x 1 u ( không xác định. x + ) 1 ( 2 x − 4)
Câu 11: Tập xác định D của hàm số y = 3x −1 là 1 1
A. D = (0;+) .
B. D = 0;+) . C. D = ; + . D. D = ; + . 3 3 Lời giải Chọn C 1
Hàm số y = 3x −1 xác định 3x −1 0 x . 3 1 Vậy: D = ; + . 3
Câu 12: Tập xác định của hàm số y = 8 − 2x − x là A. ( ;4 − . B. 4;+) . C. 0; 4 . D. 0;+) . Lời giải Chọn A
Điều kiện xác định của hàm số là 8 − 2x 0 x 4 , nên tập xác định là ( ;4 − .
Câu 13: Tập xác định của hàm số y = 4 − x + x − 2 là A. D = (2;4)
B. D = 2;4 C. D = 2; 4 D. D = (− ; 2)(4;+) Lời giải Chọn B 4 − x 0 x 4 Điều kiện:
suy ra TXĐ: D = 2;4 . x − 2 0 x 2 +
Câu 14: Tập xác định của hàm số 3x 4 y = là x −1 A. \ 1 . B. . C. (1; +) . D. 1; +) . Lời giải Chọn C x −1 0 x −1 0
Điều kiện xác định của hàm số là
x −1 0 x 1. x −1 0 x −1 0
Vậy tập xác định của hàm số là D = (1; +) .
Cách khác: Điều kiện xác định của hàm số là x −1 0 x 1.
Vậy tập xác định của hàm số là D = (1; +) . 1
Câu 15: Tập xác định của hàm số y = 3 − là x
A. D = 3; +).
B. D = (3; +). C. D = (− ; 3 . D. D = (− ; 3). Lời giải Chọn D
Điều kiện xác định 3 − x 0 x 3 . 1
Vậy tập xác định của hàm số y = D = − ; 3 . 3 − là ( ) x 1
Câu 16: Tìm tập xác định của hàm số y = x −1 + . x + 4 A. 1;+) \ 4 . B. (1;+) \ 4 . C. ( 4; − +). D. 1; +) . Lời giải Chọn D
Chuyên đề dạy thêm Toán 10 Học kì 2 Kết nối tri thức
502
251 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Chuyên đề dạy thêm Toán 10 Kết nối tri thức nhằm giúp Giáo viên có thêm tài liệu tham khảo tài liệu môn Toán 10 Kết nối tri thức.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(502 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 15 đề thi cuối kì 1 Toán 10 Chân trời sáng tạo có đáp án150.000 ₫ 2.2 K 1.1 K lượt tải
-
Bài giảng Powerpoint Toán 10 Kết nối tri thức300.000 ₫ 4.4 K 2.2 K lượt tải
-
Bộ 15 đề thi cuối kì 1 Toán 10 Kết nối tri thức có đáp án150.000 ₫ 6.9 K 3.4 K lượt tải
-
Bài giảng Powerpoint Toán 10 Cánh diều300.000 ₫ 3.2 K 1.6 K lượt tải
-
Giáo án Toán 10 Cánh diều (năm 2024) | Giáo án Toán 10 mới, chuẩn nhất300.000 ₫ 4.3 K 2.2 K lượt tải
-
5 đề thi Toán 10 Cuối kì 1 Kết nối tri thức cấu trúc mới90.000 ₫ 96 48 lượt tải
-
5 đề thi Toán 10 Cuối kì 1 Cánh diều cấu trúc mới90.000 ₫ 147 74 lượt tải
-
5 đề thi Toán 10 Cuối kì 1 Chân trời sáng tạo cấu trúc mới90.000 ₫ 121 61 lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 10
Xem thêm-
Bộ 13 đề thi cuối kì 1 Tiếng Anh 10 Global success có đáp án150.000 ₫ 7.9 K 3.9 K lượt tải
-
Chuyên đề dạy thêm Hóa 10 (cấu trúc mới200.000 ₫ 4.5 K 2.2 K lượt tải
-
Bộ đề thi cuối kì 1 Vật lí 10 Kết nối tri thức có đáp án50.000 ₫ 3.1 K 1.6 K lượt tải
-
Bộ 15 đề thi cuối kì 1 Ngữ Văn 10 Kết nối tri thức có đáp án150.000 ₫ 4.7 K 2.3 K lượt tải
-
Bài giảng Powerpoint Địa lí 10 Cánh diều200.000 ₫ 2.7 K 1.3 K lượt tải
-
Bộ 8 đề thi giữa kì 1 Tiếng Anh 10 Global Success có đáp án110.000 ₫ 9.7 K 4.9 K lượt tải
-
Chuyên đề dạy thêm Vật lí 10 (sách mới) năm 2023 có đáp án200.000 ₫ 4.7 K 2.3 K lượt tải
-
Bài giảng Powerpoint Vật lí 10 Kết nối tri thức200.000 ₫ 3.9 K 2 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
BÀI 15. HÀM SỐ
DẠNG 1. TẬP XÁC ĐỊNH CỦA HÀM SỐ
Câu 1: Tập xác định của hàm số
42
2018 2019y x x= − −
là
A.
( )
1;− +
. B.
( )
;0−
. C.
( )
0;+
. D.
( )
;− +
.
Lời giải
Chọn D
Hàm số là hàm đa thức nên xác định với mọi số thực
x
.
Câu 2: Trong các hàm số sau, hàm số nào có tập xác định là ?
A.
32
31y x x= + −
. B.
2
2x
y
x
+
=
. C.
2
23x
y
x
+
=
. D.
2
1
x
y
x
+
=
−
.
Lời giải
Chọn A
Hàm số
32
31y x x= + −
là hàm đa thức bậc ba nên tập xác định là .
Câu 3: Tập xác định của hàm số
1
1
x
y
x
+
=
−
là:
A. .
B. .
C. .
D.
( )
1; +
.
Lời giải
Chọn C
Điều kiện xác định:
1 0 1xx−
Vậy tập xác định của hàm số
1
1
x
y
x
+
=
−
là
D \ 1=
Câu 4: Tập xác định của hàm số
3
22
x
y
x
−
=
−
là
A.
\1
. B.
\3
. C.
\2
. D.
( )
1; +
.
CHƯƠNG
VI
HÀM SỐ VÀ ĐỒ THỊ
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.
III
==
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lời giải
Chọn A
Điều kiện xác định :
2 2 0 1xx−
Nên tập xác định của hàm số là :
\1D =
.
Câu 5: Tập xác định của hàm số
( )
2
2
3
x
y
x
+
=
−
là
A.
( )
;3−
. B.
( )
3; +
. C.
\3
. D. .
Lời giải
Chọn C
Điều kiện:
3 0 3.xx−
TXĐ:
\ 3 .
Câu 6: Tập xác định
D
của hàm số
31
22
x
y
x
−
=
−
là
A.
D =
. B.
)
1;D = +
. C.
( )
1;D = +
. D.
\1DR=
.
Lời giải
Chọn D
Hàm số
31
22
x
y
x
−
=
−
xác định khi
1x
. Vậy
\1DR=
.
Câu 7: Tập xác định của hàm số
2
5
1
=
−
y
x
là
A.
\1−
. B.
\ 1;1−
. C.
\1
. D. .
Lời giải
Chọn B
Hàm số đã cho xác định khi
2
1
10
1
−
−
x
x
x
.
Vậy tập xác định của hàm số là
\ 1;1=−D
.
Câu 8: Tập xác định của hàm số
51
()
15
xx
fx
xx
+−
=+
−+
là
A.
D =
. B.
1}.\{D =
C.
.{}\5D =−
D.
\ 5; 1 .{}D =−
Lời giải
Chọn D
Điều kiện:
1 0 1
5 0 5
xx
xx
−
+ −
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy tập xác định của hàm số là:
\ 1; 5D =−
.
Câu 9: Tập xác định của hàm số
2
3
56
x
y
xx
−
=
−−
là
A.
\ 1;6D =−
B.
\ 1; 6D =−
C.
1;6D =−
D.
1; 6D =−
Lời giải
Chọn A
Điều kiện
2
1
5 6 0
6
x
xx
x
−
− −
.
Vậy
\ 1;6D =−
.
Câu 10: Tìm tập xác định D của hàm số
( )
( )
2
1
14
x
y
xx
+
=
+−
.
A.
\2D =
B.
\2D =
C.
\ 1;2D =−
D.
\ 1; 2D = −
Lời giải
Chọn D
Điều kiện xác định:
2
10
1
2
40
x
x
x
x
+
−
−
. Vậy
\ 1; 2D = −
.
Lưu ý: Nếu rút gọn
2
1
4
y
x
=
−
rồi khẳng định
\2D =
là sai. Vì với
1x =−
thì biểu thức
ban đầu
( )
( )
2
1
14
x
xx
+
+−
không xác định.
Câu 11: Tập xác định
D
của hàm số
31yx=−
là
A.
( )
0;D = +
. B.
)
0;D = +
. C.
1
;
3
D
= +
. D.
1
;
3
D
= +
.
Lời giải
Chọn C
Hàm số
31yx=−
xác định
1
3 1 0
3
xx −
.
Vậy:
1
;
3
D
= +
.
Câu 12: Tập xác định của hàm số
82= − −y x x
là
A.
(
;4−
. B.
)
4;+
. C.
0;4
. D.
)
0;+
.
Lời giải
Chọn A
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Điều kiện xác định của hàm số là
8 2 0−x
4x
, nên tập xác định là
(
;4−
.
Câu 13: Tập xác định của hàm số
42y x x= − + −
là
A.
( )
2;4D =
B.
2;4D =
C.
2;4D =
D.
( ) ( )
;2 4;D = − +
Lời giải
Chọn B
Điều kiện:
40
20
x
x
−
−
4
2
x
x
suy ra TXĐ:
2;4D =
.
Câu 14: Tập xác định của hàm số
34
1
x
y
x
+
=
−
là
A.
\1
. B. . C.
( )
1; +
. D.
)
1; +
.
Lời giải
Chọn C
Điều kiện xác định của hàm số là
10
10
1 0 1
10
10
x
x
xx
x
x
−
−
−
−
−
.
Vậy tập xác định của hàm số là
( )
1;D = +
.
Cách khác: Điều kiện xác định của hàm số là
1 0 1− xx
.
Vậy tập xác định của hàm số là
( )
1;D = +
.
Câu 15: Tập xác định của hàm số
1
3
y
x
=
−
là
A.
)
3; .D = +
B.
( )
3; .D = +
C.
(
;3 .D = −
D.
( )
;3 .D = −
Lời giải
Chọn D
Điều kiện xác định
3 0 3xx−
.
Vậy tập xác định của hàm số
1
3
y
x
=
−
là
( )
;3 .D = −
Câu 16: Tìm tập xác định của hàm số
1
1
4
yx
x
= − +
+
.
A.
)
1; \ 4+
. B.
( )
1; \ 4+
. C.
( )
4;− +
. D.
)
1; +
.
Lời giải
Chọn D
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Điều kiện xác định của hàm số:
1 0 1
4 0 4
xx
xx
−
+ −
.
Suy ra tập xác định của hàm số là
)
1; +
.
Câu 17: Tìm tập xác định
D
của hàm số
23y x x= + − +
.
A.
)
3;D = − +
. B.
)
2;D = − +
. C.
D =
. D.
)
2;D = +
.
Lời giải
Chọn B
Hàm số xác định khi và chỉ khi
20
2.
30
x
x
x
+
−
+
Vậy
)
2;D = − +
.
Câu 18: Tìm tập xác định
D
của hàm số
6 3 1y x x= − − −
.
A.
( )
1;2D =
. B.
1;2D =
. C.
1;3D =
. D.
1;2D =−
.
Lời giải
Chọn B
Hàm số xác định khi và chỉ khi
6 3 0 2
.
1 0 1
xx
xx
−
−
Vậy
1;2D =
.
Câu 19: Tìm tập xác định
D
của hàm số
4
2
4
yx
x
= − −
+
.
A.
4;2D =−
. B.
(
4;2D =−
. C.
)
4;2D = −
. D.
(
2;4D =−
.
Lời giải
Chọn B
Hàm số xác định khi và chỉ khi
2 0 2
.
4 0 4
xx
xx
−
+ −
Vậy
(
4;2D =−
.
Câu 20: Tập xác định của hàm số
2
42
12
xx
y
xx
− + +
=
−−
là
A.
2;4−
. B.
( ) ( )
3; 2 2;4− − −
. C.
( )
2;4−
. D.
)
2;4−
.
Lời giải
Chọn D
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
ĐKXĐ:
2
4
40
2
2 0 2 4
3
12 0
4
x
x
x
xx
x
xx
x
−
−
+ −
−
− −
. Vậy, tập xác định của hàm số là
)
2;4D =−
Câu 21: Tập xác định của hàm số
1
3
3
yx
x
= − +
−
là:
A.
\3D =
. B.
)
3;D = +
. C.
( )
3;D = +
. D.
( )
;3D = −
.
Lời giải
Chọn C
Tập xác định của hàm số là những giá trị
x
thỏa mãn:
30
3
30
x
x
x
−
−
.
Câu 22: Tập xác định của hàm số
2
31
56
− + +
=
−+
xx
y
xx
là
A.
)
1;3 \ 2−
. B.
1;2−
. C.
1;3−
. D.
( )
2;3
.
Lời giải
Chọn A
Hàm số xác định
)
2
3
30
1
1 0 1;3 \ 2
3
5 6 0
2
−
−
+ −
− +
x
x
x
xx
x
xx
x
.
Vậy tập xác định
)
1;3 \ 2=−D
.
Câu 23: Tập xác định của hàm số
52
( 2) 1
x
y
xx
−
=
−−
là
A.
5
1; \{2}
2
. B.
5
;
2
+
. C.
5
1; \{2}
2
. D.
5
1;
2
.
Lời giải
Chọn A
Hàm số xác định khi:
5 2 0
20
10
10
x
x
x
x
−
−
−
−
5
2
2
1
1
x
x
x
x
5
1
2
2
x
x
Câu 24: Tập xác định của hàm số
( )
52
21
x
y
xx
−
=
−−
là
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
5
12
2
;\
. B.
5
2
;
+
. C.
5
12
2
;\
. D.
5
1
2
;
.
Lời giải
Chọn A
Hàm số có điều kiện xác định là:
5
5 2 0
5
2
1
2 0 2
2
2
1 0 1
x
x
x
xx
x
xx
−
−
−
Vây tập xác định của hàm số là:
5
12
2
D ; \
=
.
Câu 25: Tập xác định
D
của hàm số
( )
22xx
fx
x
− + +
=
là
A.
2;2 \ 0D =−
. B.
2;2D =−
. C.
( )
2;2D =−
. D.
D =
.
Lời giải
Chọn A
Điều kiện xác định của hàm số là
2 0 2
2 0 2
00
xx
xx
xx
−
+ −
.
Tập xác định của hàm số
2;2 \ 0D =−
.
Câu 26: Tập xác định của hàm số
35
4
1
x
y
x
+
=−
−
là
(
;ab
với
,ab
là các số thực. Tính tổng
ab+
.
A.
8ab+ = −
. B.
10ab+ = −
. C.
8ab+=
. D.
10ab+=
.
Lời giải
Chọn D
Điều kiện xác định:
1 0 1
3 5 9
4 0 0
11
xx
xx
xx
−
+−
−
−−
( )( )
1
19
9 1 0
x
x
xx
− −
.
* Tập xác định
(
1;9 1, 9 10D a b a b= → = = → + =
.
Câu 27: Tìm tập xác định của hàm số
1 2 3y x x x= + + + + +
.
A.
)
1; .− +
B.
)
2;− +
. C.
)
3;− +
. D.
)
0; .+
Lời giải
Chọn A
1 0 1
2 0 2 1
3 0 3
xx
x x x
xx
+ −
+ − −
+ −
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 28: Tập xác định
D
của hàm số
2 4 3y x x= + + −
là
A.
( )
2;3 .D =−
B.
)
3; .D = − +
C.
(
;3 .D = −
D.
2;3 .D =−
Lời giải
Chọn D
Để hàm số
2 4 3y x x= + + −
xác định thì
2 0 2
2;3 .
3 0 3
xx
x
xx
+ −
−
−
Câu 29: Tập xác định của hàm số
2 3 3 2y x x= − − −
là
A.
. B.
3
;2
2
. C.
2; )[ +
. D.
3
;2
2
.
Lời giải
Chọn D
Điều kiện
3
2 3 0
3
;2
2
20
2
2
x
x
x
x
x
−
−
.
Câu 30: Tìm tập xác định
D
của hàm số
6
43
=
−
x
y
x
A.
4
;
3
= −
D
. B.
34
;
23
=
D
. C.
23
;
34
=
D
. D.
4
;
3
= +
D
.
Lời giải
Chọn A
Điều kiện xác định:
4
4 3 0
3
− xx
.
Câu 31: Tập xác định của hàm số
1
9
25
yx
x
= + −
−
là
A.
5
;9
2
D
=
. B.
5
;9
2
D
=
. C.
5
;9
2
D
=
. D.
5
;9
2
D
=
.
Lời giải
Chọn A
Điều kiện xác định:
9
90
5
9.
5
2 5 0
2
2
x
x
x
x
x
−
−
Tập xác định:
5
;9
2
D
=
.
Câu 32: Tìm tập xác định
D
của hàm số
( )
1
3 2 1
x
y
xx
+
=
−−
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
A.
1
; \ 3
2
D
= − +
. B.
D =
. C.
1
; \ 3
2
D
= +
. D.
1
; \ 3
2
D
= +
.
Lời giải
Chọn C
Điều kiện xác định:
3
30
1
2 1 0
2
x
x
x
x
−
−
.
Vậy tập xác định của hàm số đã cho là:
1
; \ 3
2
D
= +
.
Câu 33: Hàm số nào sau đây có tập xác định là ?
A.
2
2
4
x
y
x
=
+
. B.
22
13y x x= − + −
.
C.
2
3
4
x
y
x
=
−
. D.
2
2 1 3y x x= − − −
.
Lời giải
Chọn B
2
2
4
x
y
x
=
+
có tập xác định là
( )
0; +
.
2
3
4
x
y
x
=
−
có tập xác định là
\ 2; 2−
.
2
2 1 3y x x= − − −
có tập xác định là
)
1; +
.
Câu 34: Tìm tập xác định của hàm số
2
31
1
( 4) 5
x
yx
xx
−
= − −
−−
.
A.
1;5 \ 2
. B.
( ;5]−
. C.
[1;5)\ 2
. D.
[1; ) \ 2;5+
.
Lời giải
Chọn C
Điều kiện xác định
2
10
( 4) 5 0
50
x
xx
x
−
− −
−
x [1;5)\ 2
.
Câu 35: Tập xác định
D
của hàm số
( )
34
24
x
y
xx
+
=
−+
là
A.
( )
4; \ 2D = − +
. B.
)
4; \ 2D = − +
.
C.
D =
. D.
\2D =
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lời giải
Chọn A
Hàm số
( )
34
24
x
y
xx
+
=
−+
xác định khi và chỉ khi
2 0 2
4 0 4
xx
xx
−
+ −
.
Vậy tập xác định của hàm số là
( )
4; \ 2D = − +
.
Câu 36: Tập xác định
D
của hàm số
( )
4
1 3 2
x
y
xx
+
=
+−
là
A.
3
4; .
2
D
=−
B.
3
4; .
2
D
=−
C.
3
;.
2
D
= −
D.
)
3
4; 1 1; .
2
D
= − − −
Lời giải
Chọn D
Để hàm số
( )
4
1 3 2
x
y
xx
+
=
+−
xác định thì:
)
4 0 4
3
1 0 1 4; 1 1;
2
3 2 0 3
2
xx
x x x
x
x
+ −
+ − − − −
−
.
Câu 37: Tập xác định của hàm số
( )
1
3
1
f x x
x
= − +
−
là
A.
(
1; 3D =
. B.
( )
)
;1 3;D = − +
.
C.
1;3D =
. D.
D =
.
Lời giải
Chọn A
Hàm số xác định khi
30
10
x
x
−
−
3
1
x
x
13x
.
Vậy tập xác định của hàm số là
(
1; 3D =
.
Câu 38: Tìm tập xác định
D
của hàm số
4
6
5 10
yx
x
= − +
−
.
A.
(
;6 \ 2D = −
. B.
\2
. C.
)
6;D = +
. D.
(
;6D = −
.
Lời giải
Chọn A
ĐKXĐ:
60
5 10 0
x
x
−
−
6
2
x
x
. Vậy tập xác định của hàm số là
(
;6 \ 2 .D = −
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 39: Cho hàm số
( )
1
1
3
f x x
x
= − +
−
. Tập nào sau đây là tập xác định của hàm số
( )
fx
?
A.
( )
1; +
. B.
)
1; +
. C.
) ( )
1;3 3; +
. D.
( )
1; \ 3+
.
Lời giải
Chọn C
Tập xác định là
10
13
3
x
x
x
−
.
Câu 40: Tập xác định của hàm số
( )
3 8 khi 2
7 1 khi 2
x x x
y f x
xx
− + +
==
+ +
là
A. . B.
\2
. C.
8
;
3
−
. D.
)
7;− +
.
Lời giải
Chọn A
Câu 41: Tập xác định
D
của hàm số
( )
1
2 1 3 2
22
y x x
x
= − − +
−
là
A.
13
;
22
D
=
. B.
13
; \ 1
22
D
=
. C.
3
; \ 1
2
D
= −
. D.
3
;
2
D
= −
.
Lời giải
Chọn C
Điều kiện xác định của hàm số trên là
3
3 2 0
2
2 2 0
1
x
x
x
x
−
−
.
Vậy tập xác định:
3
; \ 1
2
D
= −
.
Câu 42: Tập xác định của hàm số
3
21
y
x
=
+−
là
A.
)
2; \ 1D = − + −
. B.
\1DR=−
. C.
)
2;D = − +
. D.
( )
1;D = +
.
Lời giải
Chọn A
Hàm số xác định khi
20
21
x
x
+
+
2
1
x
x
−
−
.
Câu 43: Tập xác định của hàm số
( )
2
1
5 6 4
x
y
x x x
+
=
− + −
là
A.
)
1;4 \ 2;3 .−
B.
)
1;4 .−
C.
(
1;4 \ 2;3 .−
D.
( )
1;4 \ 2;3 .−
Lời giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Chọn A
ĐK:
)
2
1
10
2
5 6 0 1;4 \ 2;3 .
3
40
4
x
x
x
x x x
x
x
x
−
+
− + −
−
Vậy TXĐ:
)
1;4 \ 2;3 .D =−
Câu 44: Tập xác định của hàm số
2
32
x
y
xx
=
−+
là:
A.
)
0;D = +
B.
\ 1;2D =
C.
\ 1;2D
+
=
D.
( )
0;D = +
Lời giải
Chọn C
Điều kiện xác định
2
0
0
1
3 2 0
2
x
x
x
xx
x
− +
.
Vậy
\ 1;2D
+
=
.
Câu 45: Tìm tập xác định D của hàm số:
( )
23
0
2
10
khi
khi
x
x
x
y f x
xx
−
−
==
−
.
A.
\2D =
B.
)
1; \ 2D = +
C.
(
;1D = −
D.
)
1;D = +
Lời giải
Chọn C
Với
0x
thì
20x−
nên hàm số xác định với mọi
0x
.
Với
0x
: Hàm số xác định khi
1 0 1xx−
.
Vậy
(
(
(
;0 0;1 ;1D = − = −
.
Câu 46: Tập xác định của hàm số
3
2
43
= + +
−
x
yx
x
A.
)
2;= − +D
. B.
)
33
2; \ ;
44
= − + −
D
.
C.
33
;
44
=−
D
. D.
33
\;
44
=−
D
.
Lời giải
Chọn B
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Điều kiện xác dịnh của hàm số
20
4 3 0
+
−
x
x
2
3
4
3
4
−
−
x
x
x
)
33
2; \ ;
44
= − + −
D
.
Câu 47: Tìm tập xác định
D
của hàm số
3 2 6
43
xx
y
x
−+
=
−
.
A.
24
;
33
D
=
. B.
34
;
23
D
=
. C.
23
;
34
D
=
. D.
4
;.
3
D
= −
Lời giải
Chọn C
Điều kiện xác định:
2
3 2 0
24
3
4 3 0 4
33
3
x
x
x
x
x
−
−
Vậy tập xác định của hàm số là
24
;
33
D
=
.
Câu 48: Giả sử
( )
;D a b=
là tập xác định của hàm số
2
3
32
x
y
xx
+
=
− + −
. Tính
22
S a b=+
.
A.
7S =
. B.
5S =
. C.
4S =
. D.
3S =
.
Lời giải
Chọn B
Hàm số xác định khi
2
3 2 0 1 2x x x− + −
TXĐ:
( )
1;2D =
nên
22
1; 52a b S a b= = + ==
Câu 49: Hàm số
2
2
78
31
xx
y
xx
−+
=
−+
có tập xác định
\ ; ; .D a b a b=
Tính giá trị biểu thức
33
4.Q a b ab= + −
A.
11Q =
. B.
14Q =
. C.
14Q =−
. D.
10Q =
.
Lời giải
Chọn B
Hàm số
2
2
78
31
xx
y
xx
−+
=
−+
xác định khi:
2
3 1 0xx− +
.
Gọi
,ab
là
2
nghiệm của phương trình
2
3 1 0xx− + =
.
Theo Vi-et có
3
.1
ab
ab
+=
=
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Có
33
4Q a b ab= + −
( ) ( )
3
34a b ab a b ab= + − + −
27 3.3 4= − −
14=
Vậy
14Q =
.
Câu 50: Với giá trị nào của
m
thì hàm số
2
21
23
x
y
x x m
+
=
− − −
xác định trên .
A.
4m −
. B.
4m −
. C.
0m
. D.
4m
.
Lời giải
Chọn B
Hàm số
2
21
23
x
y
x x m
+
=
− − −
xác định trên khi phương trình
2
2 3 0x x m− − − =
vô nghiệm
Hay
4 0 4mm
= + −
.
Câu 51: Tập xác định của hàm số
35
4
1
x
y
x
+
=−
−
là
(
;ab
với
,ab
là các số thực. Tính tổng
ab+
.
A.
8ab+ = −
. B.
10ab+ = −
. C.
8ab+=
. D.
10ab+=
.
Lời giải
Chọn D
Ta có
( )
3 5 3 5 4 1 9
4.
1 1 1
x x x x
y
x x x
+ + − − − +
= − = =
− − −
Điều kiện xác định của hàm số:
( )
( )
9 0 9
10
1 0 1
9
0 1 9
9
1
0
9 0 9
1
1 0 1
xx
TM
x
xx
x
x
x
x
xx
L
x
xx
− +
−
−
−+
−+
−
− +
−
−
.
TXĐ:
(1;9]D =
.
Vậy
1, 9 10.a b a b= = + =
Câu 52: Tập tất cả các giá trị
m
để hàm số
2
1
23
y x m
xx
= + −
− − +
có tập xác định khác tập rỗng là
A.
( )
;3−
. B.
( )
3;− +
. C.
( )
;1−
. D.
(
;1−
.
Lời giải
Chọn C
Hàm số xác định khi và chỉ khi
2
31
2 3 0
0
x
xx
xm
xm
−
− − +
−
Để hàm số có tập xác định khác tập rỗng thì
1m
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 53: Cho hàm số
( )
2
2019 2020
,
2 21 2
x
fx
x x m
+
=
− + −
với
m
là tham số. Số các giá trị nguyên dương của tham
số
m
để hàm số
( )
fx
xác định với mọi
x
thuộc là
A. vô số. B.
9.
C.
11.
D.
10.
Lời giải
Chọn B
Hàm số
( )
fx
xác định với mọi
x
thuộc
2
2 21 2 0, .x x m x − + −
Phương trình
2
2 21 2 0x x m− + − =
vô nghiệm
( )
1 21 2 0 10.mm
= − −
Vì
m
là số nguyên dương nên
1; 2;3;...;8;9 .m
Vậy có 9 giá trị nguyên dương của
m
thỏa đề bài.
Câu 54: Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
22xm
y
xm
++
=
−
xác định trên khoảng
( )
1;0−
.
A.
0
1
m
m
−
. B.
1m −
. C.
0
1
m
m
−
. D.
0m
.
Lời giải
Chọn C
Hàm số đã cho xác định
xm
.
Khi đó tập xác định của hàm số là:
( ) ( )
;;D m m= − +
.
Yêu cầu bài toán
( )
0
1;0
1
m
D
m
−
−
.
Câu 55: Tìm giá trị của tham số
m
để hàm số
1
21
x
y
xm
+
=
−+
xác định trên nửa khoảng
(
0;1
.
A.
1
2
1
m
m
. B.
1
2
1
m
m
. C.
1
2
1
m
m
. D.
1
2
1
m
m
.
Lời giải
Chọn B
Hàm số xác định khi
2 1 0 2 1x m x m− + −
.
Hàm số xác định trên
(
(
1
2 1 0
0;1 2 1 0;1
2
2 1 1
1
m
m
m
m
m
−
−
−
.
Câu 56: Tìm giá trị của tham số
m
để hàm số
2
1
2
y
x x m
=
−−
xác định trên
2;3 .
A.
0m
. B.
03m
. C.
0m
. D.
3m
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lời giải
Chọn A
Điều kiện:
2
2 0, 2;3x x m x− −
( )
( )
2
1 1, 2;3 *x m x − +
Ta có:
23x
1 1 2x −
( )
2
1 1 4x −
( )
2
1 1, 2;3xx −
, dấu bằng xảy ra khi
( )
2 **x =
.
Từ
( )
*
và
( )
**
, ta suy ra:
1 1 0mm+
.
Vậy
0.m
Câu 57: Tìm tất cả các giá trị của
m
để hàm số
2
1
x
y
xm
=
−+
xác định trên khoảng
( )
0;2
?
A.
13m
. B.
1
5
m
m
. C.
35m
. D.
1
3
m
m
.
Lời giải
Chọn D
Hàm số
2
1
x
y
xm
=
−+
xác định khi
1 0 1x m x m− + −
.
Hàm số xác định trên khoảng
( )
0;2
khi và chỉ khi
1 0 1
1 2 3
mm
mm
−
−
.
Câu 58: Tìm tất cả các giá trị của
m
để hàm số
1
2 3 2
24
x
y x m
xm
+
= − + + +
+−
xác định trên
( )
;2− −
.
A.
2;4m−
. B.
(
2;3m−
. C.
2;3m−
. D.
(
;2m − −
.
Lời giải
Chọn C
Hàm số xác định
2 3 2 0
2 4 0
xm
xm
− + +
+ −
32
2
42
m
x
xm
+
−
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Hàm số xác định trên
( )
;2− −
( )
32
2
2
4 2 ; 2
m
m
+
−
− − −
4 3 2
4 2 2
m
m
− +
− −
2
3
m
m
−
23m −
.
Câu 59: Tìm tất cả các giá trị thực của tham số
m
để hàm số
21
mx
y
xm
=
− + −
xác định trên
( )
0;1
.
A.
(
; 1 2m − −
. B.
3
;2
2
m
−
. C.
(
;1 2m −
. D.
(
;1 3m −
.
Lời giải
Chọn C
Hàm số xác định trên
( ) ( )
20
0;1 0;1
2 1 0
xm
x
xm
− +
− + −
( ) ( )
2
2
0;1 0;1
1
21
xm
xm
xx
xm
xm
−
−
−
− +
2 0 2
1
1 1 2
2
1 0 1
mm
m
mm
m
mm
−
−
=
−
Vậy
(
;1 2m −
.
Câu 60: Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
2
( ) 3 4y f x x mx= = − +
có tập xác
định là
D =
.
A.
4
3
m
. B.
4
3
m
. C.
4
3
m
. D.
4
3
m
.
Lời giải
Chọn B
Điều kiện:
2
3 4 0x mx− +
.
YCBT
2
3 4 0,x mx x− +
.
2
2
2
9 16 4
00
4 4 3
m
m
a
− − +
.
Câu 61: Tìm m để hàm số
( )
2 3 1y x x m= − − −
xác định trên tập
( )
1; +
?
A.
2m
. B.
2m
. C.
2m
. D.
2m
.
Lời giải
Chọn B
ĐK:
11
;
33
mm
xD
++
= +
.
Để hàm số xác định trên
( )
1; +
thì
( )
11
1; ; 1 1 3 2
33
mm
mm
++
+ + +
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 62: Tất cả các giá trị của tham số
m
để hàm số
2 3 3 1
5
x m x
y
xm
xm
− + −
=+
−
− + +
xác định trên khoảng
( )
0;1
là
A.
3;0 0;1m −
. B.
3
1;
2
m
.
C.
3;0m−
. D.
3
4;0 1;
2
m
−
.
Lời giải
Chọn D
Điều kiện xác định của hàm số là:
2 3 0 2 3
0
5 0 5
x m x m
x m x m
x m x m
− + −
−
− + + +
.
TH1.
2 3 5 8m m m− +
tập xác định của hàm số là:
8Dm=
loại.
TH2.
2 3 5 8m m m− +
TXĐ của hàm số là:
)
2 3; 5 \D m m m= − +
.
Để hàm số xác định trên khoảng
( )
0;1
thì
( )
0;1 D
.
3
2 3 0
40
2
5 1 4
3
1
00
2
11
m
m
m
mm
m
mm
mm
−
−
+ −
.
Suy ra
3
4;0 1;
2
m
−
.
Câu 63: Tìm m để hàm số
2
21
2x 1
x
y
xm
+
=
+ − +
có tập xác định là .
A.
1m
. B.
0m
. C.
2m
. D.
3m
Lời giải
Chọn B
Hàm số có tập xác định khi
2
2 1 0, 1 1 0 0x x m x m m+ − + = + −
.
Câu 64: Cho hàm số
( )
22
1
2 1 2
x
y
x m x m m
+
=
− + + +
. Tập các giá trị của
m
để hàm số xác định trên
)
0;1
là
( )
)
)
; ; ;T a b c d= − +
. Tính
P a b c d= + + +
.
A.
2P =−
. B.
1P =−
. C.
2P =
. D.
1P =
.
Lời giải
Chọn A
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Hàm số xác định khi
( )
22
2 1 2 0
2
xm
x m x m m
xm
− + + +
+
.
Do đó tập xác định của hàm số là
\ 2;D m m=+
.
Vậy để hàm số xác định trên
)
0;1
điều kiện là:
)
2 0 2
; 2 0;1 1 1
0 1 2 1 0
mm
m m m m
m m m
+ −
+
+ −
.
Câu 65: Tìm các giá trị thực của tham số
m
để hàm số
2xm
y
xm
++
=
−
xác định trên
( )
1;2−
.
A.
1
2
m
m
−
. B.
1
2
m
m
−
. C.
1
2
m
m
−
. D.
12m−
.
Lời giải
Chọn B
Hàm số xác định khi
0x m x m−
.
Do đó hàm số xác định trên
( )
1;2−
( )
1
1;2
2
m
m
m
−
−
.
Câu 66: Tìm tất cả các giá trị của m để hàm số
12y x m x m= − + + −
xác định với
0x
.
A.
1m
. B.
0m
. C.
0m
. D.
1m
.
Lời giải
Chọn B
Điều kiện
1
10
20
2
xm
xm
m
xm
x
−
− +
−
.
Hàm số xác định với
10
00
0
2
m
xm
m
−
.
Câu 67: Tập hợp tất cả giá trị của tham số
m
để hàm số
21y x m= − +
xác định với mọi
1;3x
là:
A.
2
. B.
1
. C.
( ;2]−
. D.
( ;1]−
.
Lời giải
Chọn D
Hàm số xác định khi
2 1 0 2 1x m x m− + −
.
Hàm số xác định với mọi
1;3x
thì
2 1 1 1mm−
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 68: Tìm tất cả các giá trị của m để hàm số
1
2
5
y x m
x
= − + +
−
có tập xác định
)
0;5D =
.
A.
0m
. B.
2m
. C.
2m −
. D.
2m =
.
Lời giải
Chọn D
Điều kiện xác định của hàm số đã cho là
20
50
xm
x
− +
−
2
5
xm
x
−
Hàm số có tập xác định
)
0;5D =
2 0 2.mm − = =
Câu 69: Tìm tất cả các giá trị của
m
để hàm số
2
1
32
m
y
x x m
+
=
−+
có tập xác định
D =
.
A.
1
1
3
m−
. B.
1m −
. C.
1
3
m
. D.
1
3
m
.
Lời giải
Chọn C
Hàm số
2
1
32
m
y
x x m
+
=
−+
có tập xác định
D =
2
1
10
11
1
1
' 0 1 3 0
3
3 2 0,
3
m
m
mm
m
m
m
x x m x
−
+
− −
−
− +
.
Câu 70: Tìm điều kiện của m để hàm số
2
y x x m= − +
có tập xác định
D =
A.
1
4
m
. B.
1
4
m
. C.
1
4
−m
. D.
1
4
m
.
Lời giải
Chọn A
Hàm số
2
y x x m= − +
có tập xác định
D =
.
2
0,x x m x − +
( )
0 do 1
0, 1 4
a Ñ a
m
=
= −
1
4
m
.
Vậy
1
4
m
thỏa yêu cầu bài.
Câu 71: Tìm
m
để hàm số
( )
2 2 3 2
3
5
x m x
y
xm
xm
− + −
=+
−
− + +
xác định trên khoảng
( )
0;1
.
A.
3
1;
2
m
. B.
3;0m−
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C.
3;0 0;1m −
. D.
3
4;0 1;
2
m
−
.
Lời giải
Chọn D
*Gọi
D
là tập xác định của hàm số
( )
2 2 3 2
3
5
x m x
y
xm
xm
− + −
=+
−
− + +
.
*
Dx
0
2 3 0
50
xm
xm
xm
− +
−
− + +
=
23
5
m
xm
x
xm
−
+
=
.
*Hàm số
2 3 3 1
5
x m x
y
xm
xm
− + −
=+
−
− + +
xác định trên khoảng
( )
0;1
( )
0;1 D
( )
2 3 0
51
0;1
m
m
m
−
+
3
2
4
1
0
m
m
m
m
−
3
4;0 1;
2
m
−
.
Câu 72: Cho hàm số
( )
2 1 4 2
2
x
f x x m m= + − + − −
xác định với mọi
0;2x
khi
;m a b
. Giá
trị của tổng
ab+
bằng
A.
2
. B.
3
. C.
4
. D.
5
.
Lời giải
Chọn A
Hàm số
( ) 2 1 4 2
2
x
f x x m m= + − + − −
xác định khi:
12
84
xm
xm
−
−
Hàm số xác định trên [0; 2] nên
13
1 2 0 2 8 4
22
m m m− −
13
;
22
m
2ab + =
Câu 73: Tìm
m
để hàm số
1
2 3 2
2 4 8
x
y x m
xm
+
= − + + +
+−
xác định trên khoảng
( )
;2− −
.
A.
2;4m−
. B.
)
2;3m−
. C.
(
2;3m−
. D.
2;3m−
.
Lời giải
Chọn D
Tập xác định của hàm số là tập hợp các giá trị của
x
thỏa mãn điều kiện:
2 3 2 0
2 4 8 0
xm
xm
− + +
+ −
32
2
42
m
x
xm
+
−
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Để hàm số xác định trên khoảng
( )
;2− −
cần có:
32
2
2
4 2 2
m
m
+
−
− −
2
3
m
m
−
2;3m −
.
Câu 74: Có bao nhiêu giá trị nguyên âm của tham số m để tập xác định của hàm số
2
7 1 2
2
y m x
xm
= + + −
−
chứa đoạn
1;1−
?
A. 0 B. 1 C. 2 D. Vô số
Lời giải
Đáp án A.
Hàm số xác định khi và chỉ khi:
2
20
71
7 1 2 0
2
xm
xm
m
mx
x
−
+
+ −
.
Để tập xác định của hàm số chứa đoạn
1;1−
thì ta phải có
71
1/ 7
1
2
1
1/ 2
21
2
1/ 2
21
m
m
m
m
m
m
m
+
−
−
.
Vậy không có giá trị nguyên âm nào của m thỏa mãn yêu cầu bài toán.
Câu 75: Cho hàm số
12y x m x= + + −
với
2m −
. Có bao nhiêu giá trị của tham số m để tập xác định
của hàm số có độ dài bằng 1?
A. 1 B. 2 C. 3 D. 4
Lời giải
Đáp án A.
Điều kiện xác định của hàm số:
1
10
1
20
2
2
x
x
m
x
m
mx
x
−
+
−
−
.
Vậy
1;
2
m
D
=−
. Độ dài của D bằng 1 khi và chỉ khi
( )
1 1 0
2
m
m− − = =
.
Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.
DẠNG 2. XÁC ĐỊNH SỰ BIẾN THIÊN CỦA HÀM SỐ CHO TRƯỚC
Câu 76: Chọn khẳng định đúng?
A. Hàm số
()y f x=
được gọi là nghịch biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x
.
B. Hàm số
()y f x=
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
C. Hàm số
()y f x=
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x
.
D. Hàm số
()y f x=
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
; , ( ) ( )x x K x x f x f x
.
Lời giải
Chọn D
Lí thuyết định nghĩa hàm số đồng biến, nghịch biến
Câu 77: Trong các hàm số sau, hàm số nào là hàm đồng biến trên ?
A.
12yx=−
B.
32yx=+
C.
2
21y x x= + −
D.
( )
2 2 3yx= − −
.
Lời giải
Chọn B
32yx=+
đồng biến trên vì có hệ số góc
30a =
.
Câu 78: Trong các hàm số sau, hàm số nào nghịch biến trên ?
A.
yx=
. B.
2yx=−
. C.
2yx=
. D.
1
2
yx=
Lời giải
Chọn B
Hàm số
y ax b=+
với
0a
nghịch biến trên khi và chỉ khi
0a
.
Câu 79: Xét sự biến thiên của hàm số
( )
3
=fx
x
trên khoảng
( )
0;+
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng
( )
0;+
.
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng
( )
0;+
.
C. Hàm số đồng biến trên khoảng
( )
0;+
.
D. Hàm số không đồng biến, không nghịch biến trên khoảng
( )
0;+
.
Lời giải
Chọn A
( )
( ) ( )
( ) ( ) ( )
1 2 1 2
2 1 2 1
21
2 1 2 1 2 1 2 1
, 0; :
3
3 3 3
0
+
− − −
− = − = = −
−
x x x x
x x f x f x
f x f x
x x x x x x x x
Vậy hàm số nghịch biến trên khoảng
( )
0;+
.
Câu 80: Hàm số
21
1
x
y
x
+
=
−
nghịch biến trên khoảng nào trong các khoảng sau?
A.
( )
;2−
. B.
1
;
2
− +
. C.
3
1;
2
−
. D.
( )
1; +
.
Lời giải
Chọn D
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Tập xác định:
\1D =
.
Lấy
( )
12
; ;1xx −
sao cho
12
xx
.
Xét
( )( )
( )
( )( )
21
1 2 1 2 1 2 2 1 2 1
12
1 2 1 2 1 2
3
2 1 2 1 2 2 1 2 2 1
1 1 1 1 1 1
xx
x x x x x x x x x x
yy
x x x x x x
−
+ + − + − − + − +
− = − = =
− − − − − −
Với
( )
12
; ;1xx −
và
12
xx
, ta có
21
0xx−
;
1
10x −
;
2 1 2 1 2
1 0 0x y y y y− −
Do đó hàm số nghịch biến trên
( )
;1−
Lấy
( )
12
; 1;xx +
sao cho
12
xx
.
Xét
( )( )
( )
( )( )
21
1 2 1 2 1 2 2 1 2 1
12
1 2 1 2 1 2
3
2 1 2 1 2 2 1 2 2 1
1 1 1 1 1 1
xx
x x x x x x x x x x
yy
x x x x x x
−
+ + − + − − + − +
− = − = =
− − − − − −
Với
( )
12
; 1;xx +
và
12
xx
, ta có
21
0xx−
;
1
10x −
;
2 1 2 1 2
1 0 0x y y y y− −
Do đó hàm số nghịch biến trên
( )
1; +
.
DẠNG 3. XÁC ĐỊNH SỰ BIẾN THIÊN THÔNG QUA ĐỒ THỊ CỦA HÀM SỐ
Câu 81: Cho hàm số
( )
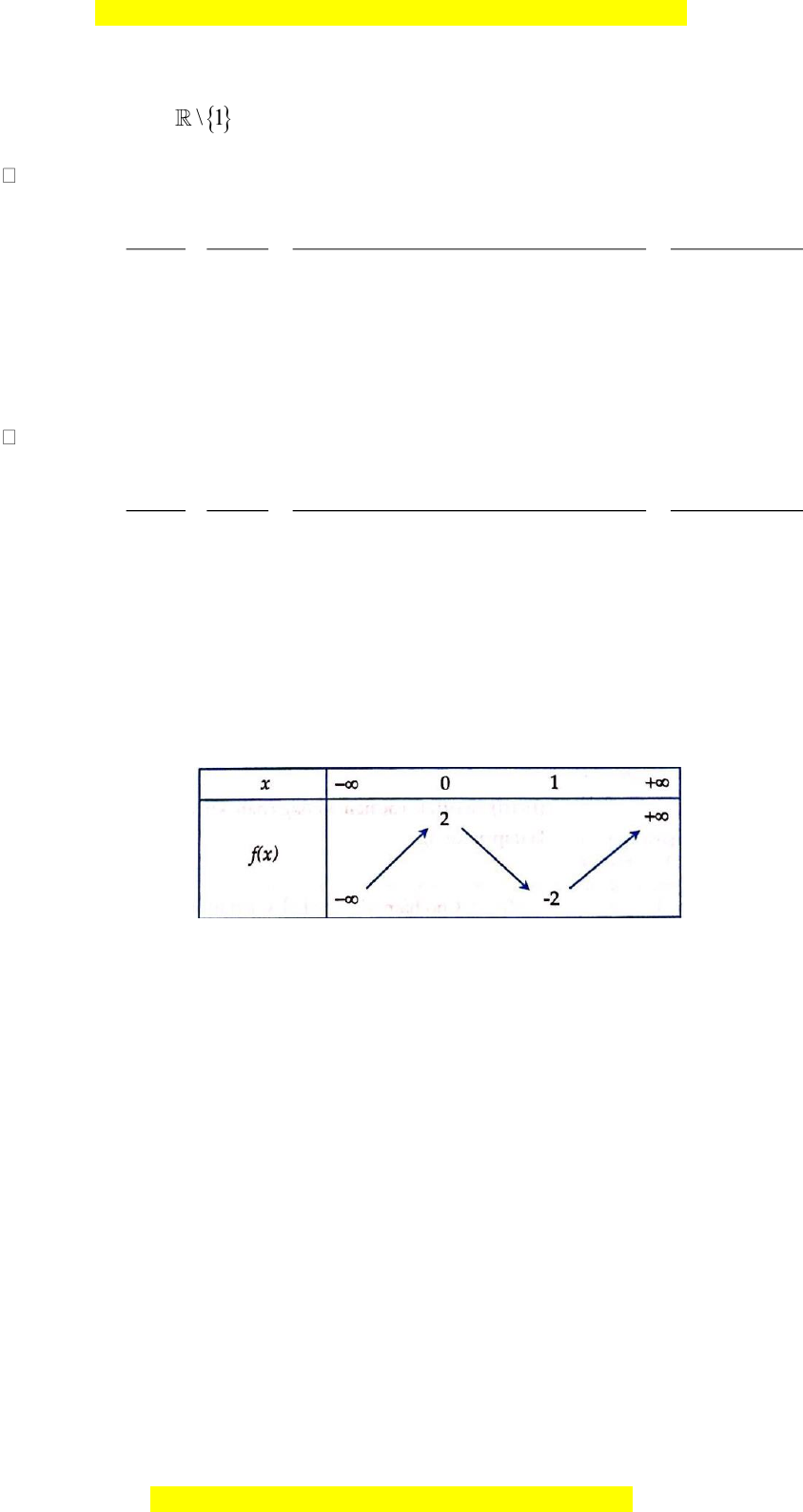
fx
có bảng biến thiên như sau
Hàm số nghịch biến trong khoảng nào dưới đây?
A.
( )
;0−
B.
( )
1; +
C.
( )
2;2−
D.
( )
0;1
Lời giải
Ta thấy trong khoảng
( )
0;1
, mũi tên có chiều đi xuống. Do đó hàm số nghịch biến trong
khoảng
( )
0;1
.
Đáp án D.
Câu 82: Cho hàm số có đồ thị như hình vẽ.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng
( )
;1− −
.
B. Hàm số đồng biến trên khoảng
( )
1; +
.
C. Hàm số nghịch biến trên khoảng
( )
1;1−
.
D. Hàm số đồng biến trên khoảng
( )
1;0−
.
Lời giải
Chọn C
Từ đồ thị hàm số ta thấy:
Hàm số nghịch biến trong các khoảng:
( )
;1− −
và
( )
0;1
.
Hàm số đồng biến trong các khoảng:
( )
1;0−
và
( )
1; +
.
Câu 83: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng
( )
0;3
. B. Hàm số đồng biến trên khoảng
( )
;1−
.
C. Hàm số nghịch biến trên khoảng
( )
0;2
. D. Hàm số đồng biến trên khoảng
( )
;3−
.
Lời giải
Chọn C
Trên khoảng
( )
0;2
, đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 84: Cho hàm số
( )
y f x=
xác định trên khoảng
( )
;− +
có đồ thị như hình vẽ dưới đây.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng
( )
0;2
B. Hàm số nghịch biến trên khoảng
( )
3;0−
C. Hàm số đồng biến trên khoảng
( )
1;0−
D. Hàm số nghịch biến trên khoảng
( )
0;3
Lời giải
Đáp án C.
Quan sát trên đồ thị ta thấy đồ thị hàm số đi lên trên khoảng
( )
1;0−
. Vậy hàm số đồng biến
trên khoảng
( )
1;0−
.
DẠNG 4. MỘT SỐ BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ CỦA HÀM SỐ
Câu 85: Trong các điểm sau đây điểm nào thuộc đồ thị của hàm số?
A.
( )
1
.2; 3M
B.
( )
2
0; 1 .M −
C.
3
11
; .
22
M
−
D.
( )
4
.1; 0M
Lời giải
Chọn B
Thay
0x =
vào hàm số ta thấy
1y =−
. Vậy
( )
2
0; 1M −
thuộc đồ thị hàm số.
Câu 86: Cho hàm số
3
32y x x= − +
. Điểm nào sau đây thuộc đồ thị hàm số đã cho?
A.
( )
2;0−
. B.
( )
1;1
. C.
( )
2; 12−−
. D.
( )
1; 1−
.
Lời giải
Chọn C
Thay tọa độ điểm vào hàm số ta thấy chỉ có điểm
( )
2;0−
thỏa mãn.
Câu 87: Cho
()P
có phương trình
2
24y x x= − +
. Điểm nào sau đây thuộc đồ thị
()P
.
A.
( )
4;2Q
. B.
( )
3;1N −
. C.
( )
4;0P =
. D.
( )
3;19M −
.
Lời giải
Chọn D
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Thử trực tiếp thấy tọa độ của
( )
3;19M −
thỏa mãn phương trình
()P
.
Câu 88: Điểm nào sau đây thuộc đồ thị hàm số
( )
1
2
x
y
xx
+
=
−
?
A.
( )
2;1M
. B.
( )
1;0N −
. C.
( )
2;0P
. D.
1
0;
2
Q
.
Lời giải
Chọn B
Đặt
( )
( )
1
2
x
fx
xx
+
=
−
Ta có:
( )
( )
11
10
1 1 2
f
−+
− = =
− − −
.
Câu 89: Điểm nào sau đây thuộc đồ thị hàm số
1
1
y
x
=
−
?
A.
( )
1
2;1M
. B.
( )
2
1;1M
. C.
( )
3
2;0M
. D.
( )
4
0; 2M −
.
Lời giải
Chọn A
Đặt
( )
1
1
fx
x
=
−
, ta có
( )
1
21
21
f ==
−
.
Câu 90: Trong các điểm sau đây, điểm nào thuộc đồ thị hàm số
32y x x= + + −
?
A.
( )
3;0M
. B.
( )
1;2N
. C.
( )
5;8 3P +
. D.
( )
5;8Q
.
Lời giải
Chọn C
Đặt
( )
32f x x x= + + −
, ta có
( )
5 5 3 5 2 8 3f = + + − = +
.
Câu 91: Điểm sau đây không thuộc đồ thị hàm số
2
44xx
y
x
−+
=
?
A.
( )
2;0A
. B.
1
3;
3
B
. C.
( )
1; 1C −
. D.
( )
1; 3D −−
.
Lời giải
Chọn C
Đặt
( )
32f x x x= + + −
, ta có
( )
5 5 3 5 2 8 3f = + + − = +
.
Câu 92: Tìm
m
để đồ thị hàm số
41y x m= + −
đi qua điểm
( )
1;2A
.
A.
6m =
. B.
1m =−
. C.
4m =−
. D.
1m =
.
Lời giải
Chọn B
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đồ thị hàm số
41y x m= + −
đi qua điểm
( )
1;2A
suy ra
2 4.1 1 1mm= + − = −
Câu 93: Đồ thị hàm số
( )
2
2 3 2
3 2
x khi x
y f x
x khi x
+
==
−
đi qua điểm có tọa độ nào sau đây ?
A.
( )
0; 3−
B.
( )
3;6
C.
( )
2;5
D.
( )
2;1
Lời giải
Chọn B
Thay tọa độ điểm
( )
0; 3−
vào hàm số ta được :
( )
0 3 3f = −
nên loại đáp án A
Thay tọa độ điểm
( )
3;6
vào hàm số ta được :
( )
3 9 3 6f = − =
, thỏa mãn nên chọn đáp án B
Câu 94: Đồ thị của hàm số
( )
2 1 2
32
khi
khi
xx
y f x
x
+
==
−
đi qua điểm nào sau đây?
A.
( )
0; 3−
B.
( )
3;7
C.
( )
2; 3−
D.
( )
0;1
Lời giải
Với
02x =
thì
( )
0 2.0 1 1yf= = + =
.
Vậy đồ thị của hàm số đã cho đi qua điểm
( )
0;1
.
Đáp án D.
Câu 95: Cho hàm số
2
2 1
.
52
1
1
x x khi x
y
x
khi x
x
−
=
−
−
Điểm nào sau đây thuộc đồ thị hàm số?
A.
( )
4; 1−
. B.
( )
2; 3−−
. C.
( )
1;3−
. D.
( )
2;1
.
Lời giải
Chọn B
Ta thấy
( )
5 2. 2
3
21
−−
=−
−−
. Nên
( )
2; 3−−
thuộc đồ thị hàm số đã cho.
Câu 96: Cho hàm số
2
2 1
.
52
1
1
x x khi x
y
x
khi x
x
−
=
−
−
Điểm nào sau đây thuộc đồ thị hàm số?
A.
( )
4; 1 .−
B.
( )
2; 3 .−−
C.
( )
1;3 .−
D.
( )
2;1 .
Lời giải
Chọn B
Ta thấy
( )
5 2. 2
3
21
−−
=−
−−
. Nên
( )
2; 3−−
thuộc đồ thị hàm số đã cho.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Câu 97: Cho hàm số
( )
2
5
xa
fx
x
+
=
+
có
( )
4 13f −=
. Khi đó giá trị của
a
là
A.
11a =
. B.
21a =
. C.
3a =−
. D.
3a =
.
Lời giải
Chọn B
Ta có
( )
( )
2. 4
4 13 21
45
a
fa
−+
− = = =
−+
.
Câu 98: Cho hàm số
( )
2
3 1; 1
2 ; 1
x x khi x
fx
x khi x
+ +
=
− +
. Tính
( )
2f −
.
A.
1−
. B.
4
. C.
7−
. D.
0
.
Lời giải
Chọn A
( )
2
3 1; 1
2 ; 1
x x khi x
fx
x khi x
+ +
=
− +
( ) ( ) ( )
2
2 2 3. 2 1 1f − = − + − + = −
.
Câu 99: Hàm số
( )
2
2 2 3
khi x 2
1
2 khi x<2
x
fx
x
x
−−
=
−
+
. Tính
( ) ( )
22P f f= + −
.
A.
3P =
. B.
7
3
P =
. C.
6P =
. D.
2P =
.
Lời giải
Chọn A
Ta có:
( ) ( )
22P f f= + −
( )
2
2 2 2 3
22
21
−−
= + − +
−
3=
.
Câu 100: Cho hàm số
( )
2
2 2 3
khi 2
1
1 khi 2
x
x
fx
x
xx
+−
=
−
+
. Tính
( ) ( )
22P f f= + −
.
A.
5
3
P =
. B.
8
3
P =
. C.
6P =
. D.
4P =
.
Lời giải
Chọn C
( ) ( ) ( )
2
2 2 2 3
2 2 2 1 6
21
P f f
+−
= + − = + − + =
−
.
Câu 101: Cho hàm số
( )
2
2 1 khi 0
3 khi 0
xx
y f x
xx
−
==
. Giá trị của biểu thức
( ) ( )
11P f f= − +
là:
A.
2−
. B.
0
. C.
1
. D.
4
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lời giải
Chọn D
( ) ( )
2
1 3. 1 3f − = − =
.
( )
1 2.1 1 1f = − =
.
Vậy
( ) ( )
1 1 3 1 4P f f= − + = + =
.
Câu 102: Cho hàm số
1
()
21
x
fx
x
−
=
−
1
1
x
x
. Giá trị của biểu thức
( 1) (1) (5)T f f f= − + +
là
A.
2T =−
. B.
7T =−
. C.
6T =
. D.
7T =
.
Lời giải
Chọn B
Vì
11−
nên
( 1) 2.( 1) 1 3f − = − − = −
, và
(1) 1 1 0f =−=
Vì
51
nên
(5) 1 5 4f = − = −
Vậy
( 1) (1) (5) 3 0 4 7T f f f= − + + = − + − = −
.
Câu 103: Cho hàm số
( )
41
4
1
34
x
khi x
fx
x
xkhi x
+−
=
−
−
. Tính
( ) ( )
55ff+−
.
A.
5
2
−
. B.
15
2
. C.
17
2
. D.
3
2
−
.
Lời giải
Chọn C
( ) ( )
5 4 1 1 17
5 5 3 5 8
5 1 2 2
ff
+−
+ − = + + = + =
−
.
Nhắn tin Zalo