Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
CHUYÊN ĐỀ 1: SO SÁNH PHÂN SỐ
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. So sánh hai phân số cùng mẫu.
- Trong hai phân số cùng mẫu dương:
+ Phân số nào có tử số lớn hơn thì lớn hơn.
+ Phân số nào có tử số bé hơn thì bé hơn.
+ Nếu tử số của hai phân số bằng nhau thì hai phân số đó bằng nhau.
2. So sánh hai phân số khác mẫu.
Muốn so sánh hai phân số khác mẫu ta quy đồng mẫu hai phân số đó, rồi thực hiện so sánh hai phân số cùng mẫu.
Lưu ý: Để thực hiện so sánh nhanh hơn nên rút gọn các phân số đã cho về dạng tối giản trước khi quy đồng.
3. Trong hai phân số có cùng tử số:
- Trong hai phân số cùng tử số dương:
+ Phân số nào có mẫu số lớn hơn thì bé hơn.
+ Phân số nào có mẫu số bé hơn thì lớn hơn.
+ Nếu mẫu số của hai phân số bằng nhau thì hai phân số đó bằng nhau. 4. Các tính chất
+ Phân số có tử và mẫu cùng dấu là phân số dương. Mọi phân số dương đều lớn hơn 0.
+ Phân số có tử và mẫu trái dấu là phân số âm. Mọi phân số âm đều nhỏ hơn 0.
+ Nếu cộng cả tử và mẫu của một phân số nhỏ hơn 1, tử và mẫu đều dương, với cùng một số nguyên + dương thì giá trị a a c
của phân số đó tăng thêm (a, , b c 0). b b + c c a c a a + c
+ Với hai phân số có cả tử và mẫu dương a và thì (a, , b , c d 0) b d b d b b + d a c b d a c e + Tính chất bắc cầu: ( , b , e f 0) c e b d f d f
+ Với mọi m 0 : a a a + m a a a + m * 1 = = b b b + * 1 . m b b b + m a a a + m a c a + c * 1 * = = . b b b + m b d b + d
PHẦN II. CÁC DẠNG BÀI.
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Dạng 1: So sánh hai phân số cùng mẫu dương
I. Phương pháp giải. a c
- Trong hai phân số có cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn: a c (b 0) b b II. Bài toán. Bài 1: So sánh các phân số sau 3 1 3 − 4 − a) và b) và 4 4 5 5 5 6 15 25 c) và d) và 7 7 37 37 Lời giải 3 1
a) Ta có: 3 1 và 4 0 nên . 4 4 3 − 4 − b) Ta có: 3
− − 4 và 5 0 nên . 5 5 5 6
c) Ta có: 6 5 và 7 0 nên . 7 7 15 25
d) Ta có: 25 15 và 27 0 nên . 37 37 Bài 2:
So sánh các phân số sau đây 3 − 1 3 − 7 a) và và 4 4 − b) 8 8 − −7 6 25 −17 c) − và d) 17 17 − và 47 47 Lời giải
Các phân số ở bài này chưa có mẫu dương, trước hết ta sẽ đưa chúng về các phân số có mẫu dương trước khi so sánh. 1 1 − 3 − 1 − 3 − 1 a) Vì = − − và 4 0 nên 4 − ; Ta có: 3 1 4 4 4 4 4 − . 7 7 − 7 − 3 − 7 3 − b) Vì = − − và 8 0 nên 8 − ; Ta có: 7 3 8 8 8 8 − . 8 7 − 7 6 7 6 7 − c) Vì = và 17 0 nên 1 − ; Ta có: 6 7 7 17 17 17 17 1 − . 7 25 2 − 5 2 − 5 1 − 7 25 1 − 7 d) Vì = − − và 47 0 nên 4 − ; Ta có: 25 17 7 47 47 47 4 − . 7 45
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải) Bài 3:
Sắp xếp các phân số sau theo thứ tự tăng dần 5 − 5 2 4 − 0 11 − 7 a) ; ; ; ; ; ; . 17 17 17 17 17 17 17 −15 5 12 14 10 −14 27 b) ; ; ; ; ; ; . 57 57 57 57 57 57 57 −15 −16 32 13 10 −18 23 c) ; ; ; ; ; ; . 37 37 37 37 37 37 37 Lời giải
Nhận xét: Các phân số trong bài có cùng mẫu số dương, nên để sắp xếp các phân số theo thứ tự tăng
dần ta so sánh các tử số. 5 − 5 2 4 − 0 11 − 7 a) ; ; ; ; ; ; . 17 17 17 17 17 17 17 1 − 1 5 − 4 − 0 2 5 7
Ta có: -11 < -5 < -4 <0 < 2 < 5< 7 và 17 > 0 nên . 17 17 17 17 17 17 17 −15 5 12 14 10 −14 27 b) ; ; ; ; ; ; . 57 57 57 57 57 57 57 1 − 5 1 − 4 5 10 12 14 27
Ta có: -15 < -14 < 5 < 10 < 12 <14 < 27 và 57 > 0 nên 57 57 57 57 57 57 57 −15 −16 32 13 10 −18 23 c) ; ; ; ; ; ; . 37 37 37 37 37 37 37
Ta có: -18 < -16 < -15 < 10 < 13 < 23 < 32 và 37 > 0 1 − 8 1 − 6 1 − 5 10 13 23 32 Nên . 37 37 37 37 37 37 37 Bài 4:
Bài 4: Điền số thích hợp vào các chỗ trống sau 10 ... ... ... ... 15 1 − 1 ... ... ... ... 6 − a) . b) . 15 15 15 15 15 15 17 17 17 17 17 17 8 − ... ... ... 4 − c) 37 3 − 7 37 3 − . 7 37 Lời giải 10 11 12 13 14 15 1 − 1 1 − 0 9 − 8 − 7 − 6 − a) . b) . 15 15 15 15 15 15 17 17 17 17 17 17 8 − 7 6 − 5 4 − c) . 37 3 − 7 37 3 − 7 37
Dạng 2: So sánh hai phân số khác mẫu
I. Phương pháp giải.
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Cách 1. Quy đồng mẫu số hai phân số rồi so sánh các tử số của chúng.
- Bước 1: Quy đồng mẫu số của hai phân số (đưa các phân số về cùng mẫu số)
- Bước 2: So sánh tử số của hai phân số cùng mẫu số đã quy đồng.
Trong hai phân số có cùng mẫu số:
+ Phân số nào có tử số nhỏ hơn thì nhỏ hơn.
+ Phân số nào có tử số lớn hơn thì lớn hơn.
Cách 2. Quy đồng tử số hai phân số rồi so sánh các mẫu số của chúng.
- Bước 1: Quy đồng tử số (đưa về cùng tử số)
+ Lấy tử số và mẫu số của phân số thứ nhất nhân tử số của phân số thứ hai.
+ Lấy tử số và mẫu số của phân số thứ hai nhân tử số của phân số thứ nhất.
- Bước 2: So sánh mẫu số của hai phân số đã quy đồng tử số.
Trong hai phân số có cùng tử số:
+ Phân số nào có mẫu số nhỏ hơn thì lớn hơn
+ Phân số nào có mẫu số lớn hơn thì nhỏ hơn.
Lưu ý: Để thực hiện so sánh nhanh hơn nên rút gọn các phân số đã cho về dạng tối giản trước khi quy đồng. II. Bài toán. Bài 1: 2 4 So sánh và 5 7 Lời giải
Cách 1: Quy đồng mẫu số 2PS rồi so sánh tử số của chúng với nhau. + Ta có: mẫu chung là 35 14 20 2 4
+ So sánh 2PS đã quy đồng, ta có :
(vì 2 PS có cùng mẫu số, tử số có 14 20 ) nên . 35 35 5 7 2 2 2 4 4
Cách 2: Chọn tử số chung là 4 (vì 4 : 2 = 2 ), ta có: = = ; 5 5 giữ nguyên 2 10 7 4 4 2 4 Ta có :
(TS = 4, mẫu số có 10 7 ) nên . 10 7 5 7 Bài 2: 3 − 4 So sánh . . và 4 5 − Lời giải Có MC: 4.5 = 20 3 − ( 3 − ).5 1 − 5 = = ; 4 4.5 20
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Chuyên đề dạy thêm Toán 6 Học kì 2 Chân trời sáng tạo
1.5 K
761 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu Chuyên đề dạy thêm Toán 6 Chân trời sáng tạo nhằm giúp Giáo viên có thêm tài liệu tham khảo tài liệu môn Toán 6 Chân trời sáng tạo.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(1521 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 15 đề thi giữa kì 1 Toán 6 Kết nối tri thức có đáp án150.000 ₫ 27.3 K 13.7 K lượt tải
-
Bộ 20 đề thi giữa kì 1 Toán 6 Cánh diều có đáp án150.000 ₫ 14 K 7 K lượt tải
-
Bộ 20 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo có đáp án150.000 ₫ 10.9 K 5.4 K lượt tải
-
Bộ 21 đề thi cuối kì 1 Toán 6 Kết nối tri thức có đáp án150.000 ₫ 30.6 K 15.3 K lượt tải
-
Bộ 20 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án150.000 ₫ 13.8 K 6.9 K lượt tải
-
Bài giảng Powerpoint Toán 6 Cánh diều300.000 ₫ 4.2 K 2.1 K lượt tải
-
Giáo án Toán 6 Kết nối tri thức (năm 2024) | Giáo án Toán 6 mới, chuẩn nhất300.000 ₫ 4.1 K 2.1 K lượt tải
-
Bộ 20 đề thi cuối kì 1 Toán 6 Chân trời sáng tạo có đáp án150.000 ₫ 10 K 5 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 6
Xem thêm-
Bộ đề thi giữa kì 1 Tiếng Anh 6 Global success có đáp án90.000 ₫ 30.7 K 15.4 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Lịch sử & Địa lý 6 Kết nối tri thức có đáp án60.000 ₫ 6.9 K 3.4 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Ngữ văn 6 Chân trời sáng tạo có đáp án150.000 ₫ 10.3 K 5.2 K lượt tải
-
Bộ 9 đề thi giữa kì 1 KHTN 6 Kết nối tri thức có đáp án130.000 ₫ 11.2 K 5.6 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Tin học 6 Kết nối tri thức năm 2024 có đáp án70.000 ₫ 8.7 K 4.4 K lượt tải
-
Bộ 20 đề thi giữa kì 1 Ngữ văn 6 Kết nối tri thức có đáp án150.000 ₫ 18.2 K 9.1 K lượt tải
-
Bộ 9 đề thi giữa kì 1 KHTN 6 Chân trời sáng tạo có đáp án130.000 ₫ 5.6 K 2.8 K lượt tải
-
Bộ 15 đề thi giữa kì 1 Ngữ văn 6 Cánh diều có đáp án150.000 ₫ 5.1 K 2.5 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
CHUYÊN ĐỀ 1: SO SÁNH PHÂN SỐ
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. So sánh hai phân số cùng mẫu.
- Trong hai phân số cùng mẫu dương:
+ Phân số nào có tử số lớn hơn thì lớn hơn.
+ Phân số nào có tử số bé hơn thì bé hơn.
+ Nếu tử số của hai phân số bằng nhau thì hai phân số đó bằng nhau.
2. So sánh hai phân số khác mẫu.
Muốn so sánh hai phân số khác mẫu ta quy đồng mẫu hai phân số đó, rồi thực hiện so sánh hai phân số
cùng mẫu.
Lưu ý: Để thực hiện so sánh nhanh hơn nên rút gọn các phân số đã cho về dạng tối giản trước khi quy
đồng.
3. Trong hai phân số có cùng tử số:
- Trong hai phân số cùng tử số dương:
+ Phân số nào có mẫu số lớn hơn thì bé hơn.
+ Phân số nào có mẫu số bé hơn thì lớn hơn.
+ Nếu mẫu số của hai phân số bằng nhau thì hai phân số đó bằng nhau.
4. Các tính chất
+ Phân số có tử và mẫu cùng dấu là phân số dương. Mọi phân số dương đều lớn hơn 0.
+ Phân số có tử và mẫu trái dấu là phân số âm. Mọi phân số âm đều nhỏ hơn 0.
+ Nếu cộng cả tử và mẫu của một phân số nhỏ hơn 1, tử và mẫu đều dương, với cùng một số nguyên
dương thì giá trị của phân số đó tăng thêm
( , , 0).
a a c
abc
b b c
+
+
+ Với hai phân số có cả tử và mẫu dương
a
b
và
c
d
thì
( , , , 0)
a c a a c
a b c d
b d b b d
+
+
+ Tính chất bắc cầu:
( , , 0)
ac
a c e
bd
b e f
ce
b d f
df
+ Với mọi m
0 :
*1
a a a m
b b b m
+
+
* 1 .
a a a m
b b b m
+
= =
+
*1
+
+
a a a m
b b b m
*.
+
==
+
a c a c
b d b d
PHẦN II. CÁC DẠNG BÀI.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Dạng 1: So sánh hai phân số cùng mẫu dương
I. Phương pháp giải.
- Trong hai phân số có cùng mẫu dương, phân số nào có tử lớn hơn thì lớn hơn:
( )
0
ac
a c b
bb
II. Bài toán.
Bài 1:
So sánh các phân số sau
a)
3
4
và
1
4
b)
3
5
−
và
4
5
−
c)
5
7
và
6
7
d)
15
37
và
25
37
Lời giải
a) Ta có:
3 1
và
4 0
nên
31
44
.
b) Ta có:
3 4− −
và
50
nên
34
55
−−
.
c) Ta có:
6 5
và
7 0
nên
56
77
.
d) Ta có:
25 15
và
27 0
nên
15 25
37 37
.
Bài 2:
So sánh các phân số sau đây
a)
3
4
−
và
1
4−
b)
3
8
−
và
7
8−
c)
7
17
−
−
và
6
17
d)
25
47−
và
17
47
−
Lời giải
Các phân số ở bài này chưa có mẫu dương, trước hết ta sẽ đưa chúng về các phân số có mẫu dương
trước khi so sánh.
a) Vì
11
44
−
=
−
; Ta có:
31− −
và
40
nên
3 1 3 1
4 4 4 4
− − −
−
.
b) Vì
77
88
−
=
−
; Ta có:
7 3− −
và
8 0
nên
7 3 7 3
8 8 8 8
− − −
−
.
c) Vì
77
17 17
−
=
−
; Ta có:
6 7
và
17 0
nên
6 7 6 7
17 17 17 17
−
−
.
d) Vì
25 25
47 47
−
=
−
; Ta có:
25 17− −
và
47 0
nên
25 17 25 17
47 47 47 45
− − −
−
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 3:
Sắp xếp các phân số sau theo thứ tự tăng dần
a)
5
17
−
;
5
17
;
2
17
;
4
17
−
;
0
17
;
11
17
−
;
7
17
.
b)
15
57
−
;
5
57
;
12
57
;
14
57
;
10
57
;
14
57
−
;
27
57
.
c)
15
37
−
;
16
37
−
;
32
37
;
13
37
;
10
37
;
18
37
−
;
23
37
.
Lời giải
Nhận xét: Các phân số trong bài có cùng mẫu số dương, nên để sắp xếp các phân số theo thứ tự tăng
dần ta so sánh các tử số.
a)
5
17
−
;
5
17
;
2
17
;
4
17
−
;
0
17
;
11
17
−
;
7
17
.
Ta có: -11 < -5 < -4 <0 < 2 < 5< 7 và 17 > 0 nên
11 5 4 0 2 5 7
17 17 17 17 17 17 17
− − −
.
b)
15
57
−
;
5
57
;
12
57
;
14
57
;
10
57
;
14
57
−
;
27
57
.
Ta có: -15 < -14 < 5 < 10 < 12 <14 < 27 và 57 > 0 nên
15 14 5 10 12 14 27
57 57 57 57 57 57 57
−−
c)
15
37
−
;
16
37
−
;
32
37
;
13
37
;
10
37
;
18
37
−
;
23
37
.
Ta có: -18 < -16 < -15 < 10 < 13 < 23 < 32 và 37 > 0
Nên
18 16 15 10 13 23 32
37 37 37 37 37 37 37
− − −
.
Bài 4:
Bài 4: Điền số thích hợp vào các chỗ trống sau
a)
10 ... ... ... ... 15
15 15 15 15 15 15
. b)
11 ... ... ... ... 6
17 17 17 17 17 17
−−
.
c)
8 ... ... ... 4
37 37 37 37 37
−−
−−
.
Lời giải
a)
10 11 12 13 14 15
15 15 15 15 15 15
. b)
11 10 9 8 7 6
17 17 17 17 17 17
− − − − − −
.
c)
8 7 6 5 4
.
37 37 37 37 37
− − −
−−
Dạng 2: So sánh hai phân số khác mẫu
I. Phương pháp giải.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Cách 1. Quy đồng mẫu số hai phân số rồi so sánh các tử số của chúng.
- Bước 1: Quy đồng mẫu số của hai phân số (đưa các phân số về cùng mẫu số)
- Bước 2: So sánh tử số của hai phân số cùng mẫu số đã quy đồng.
Trong hai phân số có cùng mẫu số:
+ Phân số nào có tử số nhỏ hơn thì nhỏ hơn.
+ Phân số nào có tử số lớn hơn thì lớn hơn.
Cách 2. Quy đồng tử số hai phân số rồi so sánh các mẫu số của chúng.
- Bước 1: Quy đồng tử số (đưa về cùng tử số)
+ Lấy tử số và mẫu số của phân số thứ nhất nhân tử số của phân số thứ hai.
+ Lấy tử số và mẫu số của phân số thứ hai nhân tử số của phân số thứ nhất.
- Bước 2: So sánh mẫu số của hai phân số đã quy đồng tử số.
Trong hai phân số có cùng tử số:
+ Phân số nào có mẫu số nhỏ hơn thì lớn hơn
+ Phân số nào có mẫu số lớn hơn thì nhỏ hơn.
Lưu ý: Để thực hiện so sánh nhanh hơn nên rút gọn các phân số đã cho về dạng tối giản trước khi quy
đồng.
II. Bài toán.
Bài 1:
So sánh
2
5
và
4
7
Lời giải
Cách 1: Quy đồng mẫu số
2PS
rồi so sánh tử số của chúng với nhau.
+ Ta có: mẫu chung là 35
+ So sánh
2PS
đã quy đồng, ta có :
14 20
35 35
(vì 2 PS có cùng mẫu số, tử số có
14 20
) nên
24
57
.
Cách 2: Chọn tử số chung là 4 (vì
4:2 2=
), ta có:
2 2 2 4
;
5 5 2 10
==
giữ nguyên
4
7
Ta có
(
44
: TS 4
10 7
=
, mẫu số có
10 7
) nên
24
57
.
Bài 2:
So sánh .
3
4
−
. và
4
5−
Lời giải
Có MC: 4.5 = 20
3 ( 3).5 15
4 4.5 20
− − −
==
;
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
4 ( 4).4 16
5 5.4 20
− − −
==
Vì: - 15 > - 16 nên
15 16
20 20
−−
hay:
34
45
−−
. Vậy:
34
45
−−
Bài 3:
So sánh các phân số:
a)
11
12
−
và
17
18−
b)
14
21
−
và
60
72
−
−
Lời giải
a)
11
12
−
và
17
18−
11
12
−
và
17
18
−
Có MC: 2
2
.3
2
= 36
11 ( 11).3 33
12 12.3 36
− − −
==
;
17 ( 17).2 34
18 18.2 36
− − −
==
Vì
33 34
36 36
−−
nên
11 17
12 18
−−
. Vậy:
11 17
12 18
−
−
b,
14
21
−
và
60
72
−
−
2
3
−
và
5
6
Có MC: 6
2 ( 2).2 4
3 3.2 6
− − −
==
Vì
45
66
−
nên
25
36
−
. Vậy
14 60
21 72
−−
−
Bài 4:
So sánh các đại lượng sau:
a) Thời gian nào dài hơn:
2
3
h
hay
3
4
h
?
b) Đoạn thẳng nào ngắn hơn
7
10
m
hay
3
4
m
?
c) Khối lượng nào lớn hơn:
79
10 10
kg hay kg
d) Vận tốc nào nhỏ hơn
57
/ / ?
69
kg h hay kg h
Lời giải
a,
2
3
h và
3
4
h có MC: 12
2 2.4 8
3 3.4 12
==
;
3 3.3 9
4 4.3 12
==
Vì
98
12 12
nên
3
4
h dài hơn
2
3
h
b,
7
10
và
3
4
có MC: 2
2
.5 = 20
7 7.2 14
10 10.2 20
==
;
3 3.5 15
4 4.5 20
==
Vì
14 15
20 20
nên
7
10
m ngắn hơn
3
4
m.
c) Ta có
9
10
>
7
10
(vì
97
)
d) Ta có
7 42
9 54
=
;
5 45
6 54
=
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
nên
9
10
kg
lớn hơn
7
10
kg
mà
42 45
42 45
54 54
vậy
7
9
km/h nhỏ hơn
5
6
km/h
Bài 5:
So sánh hai phân số
2
3
và
3
4
Lời giải
´
C a ch 1:
QĐMS (chọn
MSC 12=
)
Ta có :
2 2 4 8 3 3 3 9
;
3 3 4 12 4 4 3 12
= = = =
Vì
89
12 12
nên
23
34
´
C a ch 2:
QĐTS ( chọn
TSC 6)=
Ta có :
2 2 3 6 3 3 2 6
;
3 3 3 9 4 4 2 8
= = = =
Vì
66
98
nên
23
34
.
Bài 6:
Viết các phân số sau theo thứ tự từ bé đến lớn :
a)
8 5 17
;;
9 6 18
b)
1 3 5
;;
2 4 8
Lời giải
Để sắp xếp các PS theo thứ tự từ bé đến lớn, trước tiên ta QĐMS các PS này. Rồi so sánh tử số.
Chọn
MSC 18=
(vì 18 chia hết cho 6; 9; 18)
a)
8 8 2 16 5 5 3 15
;;
9 9 2 18 6 6 3 18
= = = =
giữ nguyên
17
18
Ta so sánh các
PS
đã quy đồng mẫu số Vì
15 16 17
18 18 18
nên
5 8 17
6 9 18
Vậy các phân số được viết theo thứ tự từ bé đến lớn là:
5 8 17
;;
6 9 18
b) Chọn
MSC 8=
(vì 8 chia hết cho 2 ; 4; 8)
Ta có: Vì
1 4 3 6
;
2 8 4 8
==
nên
153
2 8 4
, giữ nguyên
5
8
Vì
456
8 8 8
nên
153
2 8 4
Vậy các phân số được viết theo thứ tự từ bé đến lớn là :
153
;;
2 8 4
Bài 7:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Sắp xếp các phân số sau theo thứ tự giảm dần:
2 3 1 5 5
; ; ; ;
9 4 12 6 8
− − −
Lời giải
Do các số âm luôn nhỏ hơn các số dương nên
3 5 2 1 5
; ; ; ;
4 6 9 12 8
− − −
Trong các số dương thì
53
64
Vì
2 5 5
9 12 8
nên
25
98
− −
Vì
2 2 1
9 12 12
nên
21
9 12
− −
Vậy chúng ta có thể sắp xếp theo yêu cầu đề bài
5 3 1 2 5
; ; ; ; ;
6 4 12 9 8
− − −
Dạng 3: So sánh qua số trung gian
I. Phương pháp giải.
- Khi so sánh hai hay nhiều phân số, việc quy đồng đưa về cùng một mẫu số dương để so sánh tử số
nhiều khi khá khó khăn, do đó, ta có thể chọn một phân số trung gian, dựa vào phân số trung gian này,
ta sẽ so sánh được hai phân số ban đầu.
* Dạng 3.1: So sánh qua số 0
- Việc so sánh qua số 0 được sử dụng khi ta thấy một phân số nhỏ hơn 0 (tử và mẫu trái dấu) và một
phân số lớn hơn không (tử và mẫu cùng dấu).
. 0 0
( . 0)
. 0 0
a
ac
ab
c
cd
b
cd
bd
d
* Dạng 3.2: So sánh qua số 1
- Với hai phân số cùng dương mà ta nhận thấy một phân số lớn hơn 1 ( tử số lớn hơn mẫu số) và một
phân số nhỏ hơn 1 ( tử số nhỏ hơn mẫu số) thì ta sẽ chọn 1 là số trung gian để so sánh.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
1
1 ( , , , 0)
1
a
ab
ac
b
a b c d
c
bd
cd
d
* Dạng 3.3: So sánh qua một phân số trung gian phù hợp
Ta cũng có thể chọn một phân số trung gian phù hợp để so sánh hai phân số
( . . 0)
ac
a c e
bd
b e f
ce
b d f
df
Chú ý một vài tính chất sau đây:
+ Trong hai phân số có cùng tử, tử và mẫu đều dương, phân số nào có mẫu nhỏ hơn thì lớn hơn
( , , 0)
aa
c b a b c
cb
+ Nếu cộng cả tử và mẫu của một phân số nhỏ hơn 1, tử và mẫu đều dương, với cùng một số nguyên
dương thì giá trị của phân số đó tăng thêm.
( , , 0)
a a c
abc
b b c
+
+
+ Với hai phân số có cả tử và mẫu dương
a
b
và
c
d
thì
( , , , 0)
a c a a c
a b c d
b d b b d
+
+
II. Bài toán.
Bài 1:
So sánh hai phân số sau
a)
3
5
và
7
6
b)
7
15
và
4
3
c)
13
14
và
16
15
d)
23
25
và
21
19
Lời giải
a)
3
5
và
7
6
.
Ta có
35
1
3 7 3 7
55
1
76
5 6 5 6
1
66
=
=
.
b)
7
15
và
4
3
Ta có:
7 15
1
7 4 7 4
15 15
1
43
15 3 15 3
1
33
=
=
.
c)
13
14
và
16
15
.
d)
23
25
và
21
19
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có
13 14
1
13 16 13 16
14 14
1
16 15
14 15 14 15
1
15 15
=
=
.
Ta có:
23 25
1
23 21 23 21
25 25
1
21 19
25 19 25 19
1
19 19
=
=
.
Bài 2:
So sánh hai phân số sau
a)
13
5
và
7
9
−
b)
8
13−
và
1
33
c)
13
17
−
−
và
3
11
−
d)
3
25−
và
1
19
−
−
Lời giải
a) Ta có:
13 7
13.5 0 0 7.9 0 0
59
−
−
7 13 7 13
0.
9 5 9 5
−−
b) Ta có:
18
1.33 0 0 8.( 13) 0 0
33 13
−
−
8 1 8 1
0.
13 33 13 33
−−
c) Ta có:
13 3
( 13).( 17) 0 0 ( 3).11 0 0
17 11
−−
− − −
−
3 13 3 13
0.
11 17 11 17
− − − −
−−
d) Ta có:
1 3 3 1 3 1
( 1).( 19) 0 0 3.( 25) 0 0 0 .
19 25 25 19 25 19
− − −
− − −
− − − − − −
Bài 3:
So sánh hai phân số sau
a)
4
17
và
16
63
. b)
5
29
và
7
33
c)
44
57
và
89
99
d)
19
53
và
30
73
Lời giải
a) Ta có:
4 4 1 16 16
17 16 4 64 63
= =
.
b) Ta có :
5 5 1 7 7
29 25 5 35 33
= =
c) Ta có:
44 44 22 88 88 89
57 52 25 100 99 99
= =
.
d) Ta có:
19 20 20 2 30 30
53 53 50 5 75 73
= =
Bài 4:
So sánh hai phân số sau
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a)
22
107
và
18
79
. b)
25
67
và
35
89
.
c)
18
67
và
31
106
. d)
41
119
và
24
67
.
Lời giải
a) Ta có:
22 22 2 18 18
107 99 9 81 79
= =
b) Ta có:
25 25 5 35 35
.
67 65 13 91 89
= =
c) Ta có:
18 18 2 30 30
67 63 7 75 73
= =
.
d) Ta có:
41 42 6 24 24
.
119 119 17 68 67
= =
Bài 5:
So sánh hai phân số sau
a)
65
129
và
91
174
. b)
21
53
và
50
119
.
Lời giải
a) Ta có:
65 65 13 91 91
129 125 25 175 174
= =
. b) Ta có:
21 21 7 49 50
53 51 17 119 119
= =
.
Dạng 4: So sánh qua phần bù (hay phần thiếu).
I. Phương pháp giải.
So sánh qua phần bù áp dụng để so sánh hai phân số nhỏ hơn 1.
Với phân số
1
a
b
thì
1
a b a
bb
−
−=
được gọi là phần bù đến đơn vị của phân số
a
b
.Trong hai phân số
có phần bù tới đơn vị khác nhau, phân số nào có phần bù nhỏ hơn thì phân số đó lớn hơn.
II. Bài toán.
Bài 1:
Bài 1. So sánh hai phân số sau
a)
2009
2010
và
2008
2009
b)
1007
1009
và
1005
1007
c)
2021
2023
và
2017
2019
d)
2005
2007
và
2009
2011
Lời giải
a) Ta có:
b) Ta có:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
+)
2009 2010 2009 1
1
2010 2010 2010 2010
−=−=
+)
2008 2009 2008 1
1
2009 2009 2009 2009
−=−=
+)
1 1 2009 2008
.
2009 2010 2010 2009
+)
1007 1009 1007 2
1
1009 1009 1009 1009
− = − =
+)
1005 1007 1005 2
1
1007 1007 1007 1007
−=−=
+)
2 2 1005 1007
1007 1009 1007 1009
.
c) Ta có:
+)
2021 2023 2021 2
1
2023 2023 2023 2023
−=−=
+)
2017 2019 2017 2
1
2019 2019 2019 2019
− = − =
+)
2 2 2017 2021
2019 2023 2019 2023
d) Ta có:
+)
2005 2007 2005 2
1
2007 2007 2007 2007
−=−=
+)
2009 2011 2009 2
1
2011 2011 2011 2011
− = − =
+)
2 2 2005 2009
2011 2007 2007 2011
Bài 2:
So sánh hai phân số sau
a)
2005
2009
và
2007
2010
. b)
1997
1999
và
1995
1998
.
c)
2004
2005
và
2001
2004
. d)
1775
1777
và
1768
1771
Lời giải
a) Ta có:
+)
2005 2009 2005 4
1
2009 2009 2009 2009
−=−=
+)
2007 2010 2007 3
1
2010 2010 2010 2010
− = − =
+)
3 3 4 2007 2005
2010 2009 2009 2010 2009
b) Ta có:
+)
1997 1999 1997 2
1
1999 1999 1999 1999
− = − =
+)
1995 1998 1995 3
1
1998 1998 1998 1998
−=−=
+)
2 2 3
1999 1998 1998
1997 1995
1999 1998
c) Ta có:
+)
2004 2005 2004 1
1
2005 2005 2005 2005
− = − =
+)
2001 2004 2001 3
1
2004 2004 2004 2004
−=−=
+)
1 1 3 2004 2001
2005 2004 2004 2005 2004
d) Ta có:
+)
1775 1777 1775 2
1
1777 1777 1777 1777
−=−=
+)
1768 1771 1768 3
1
1771 1771 1771 1771
− = − =
+)
2 2 3 1775 1768
1777 1771 1771 1777 1771
.
Bài 3:
So sánh hai phân số sau
98
10 9
10 1 10 1
;
10 1 10 1
AB
++
==
++
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Lời giải
Ta có:
+)
9 10 9 10 9 9
10 10 10 10 10
10 1 10 1 10 1 10 10 10 .9
11
10 1 10 1 10 1 10 1 10 1
A
+ + + −
− = − = − = =
+ + + + +
+)
8 9 8 9 8 8
9 9 9 9 9
10 1 10 1 10 1 10 10 10 .9
11
10 1 10 1 10 1 10 1 10 1
B
+ + + −
− = − = − = =
+ + + + +
+) Để so sánh
1 A−
và
1 B−
, ta so sánh
10
10
10 1+
và
9
1
10 1+
9 10 10
1 10 10
10 1 10 10 10 1
=
+ + +
11B A A B − −
Bài 4:
So sánh hai phân số sau
99 98
100 99
7 2 7 2
;
7 2 7 2
AB
++
==
++
Lời giải
Ta có:
+)
99 99 99 99 98
100 100 100 100 99
7 2 5 7 1 7 2 5 7 7 7 1
1
7 2 5 7 1 7 2 5 7 7 7 1
A
+ + + + + +
= =
+ + + + + +
+)
98 98 98 98 98
99 99 99 99 99
7 1 7 1 1 7 1 7 1 1 7 2
1
7 1 7 1 1 7 1 7 1 1 7 2
+ + + + + +
=
+ + + + + +
+ Vậy
AB
.
Bài 5:
So sánh hai phân số sau
89
90
11 1
11 1
A
+
=
+
và
87
88
10 1
10 1
B
+
=
+
.
Lời giải
Ta có:
89 89 89 88
90 90 90 89
11 1 10 11 1 11 1 10 11 1
1
11 1 10 11 1 11 1 10 11 1
A
+ + + + +
=
+ + + + +
88 88 88 88 87
89 89 89 89 88
11 1 11 1 10 11 1 11 1 10 11 1
1
11 1 11 1 10 11 1 11 1 10 11 1
+ + + + + +
=
+ + + + + +
Vậy
88
89
11 1
11 1
AB
+
+
.
Bài 6:
So sánh hai phân số sau
43
49
và
31
35
Lời giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có:
43 43.4 172
49 49.4 196
==
;
31 31.6 186
35 35.6 210
==
43 172 196 172 24
11
49 196 196 196 196
− = − = − =
31 186 210 186 24
11
35 210 210 210 210
− = − = − =
24 24 43 31
196 210 49 35
.
Bài 7:
So sánh hai phân số sau
a)
12
17
và
7
15
b)
1999
2001
và
12
11
c)
13
27
và
27
41
d)
1998
1999
và
1999
2000
e)
23
47
và
24
45
g)
17
33
và
13
27
Lời giải
a) Ta có:
7 7 2 7 7 2 9 12
1.
15 15 2 15 15 2 17 17
+
=
+
Vậy
12 7
17 15
.
b) Ta có:
1999
1999 2001 1.
2001
12
12 11 1
11
1999 12 1999 12
1
2001 11 2001 11
.
c) Ta có:
13 13 1
27 26 2
=
27 27 1
41 54 2
=
Vậy
13 1 27 13 27
.
27 2 41 27 41
d) Ta có:
1998 1999 1998 1
1
1999 1999 1999 1999
−=−=
1999 2000 1999 1
1
2000 2000 2000 2000
−=−=
Mà
1 1 1998 1999
1999 2000 1999 2000
e) Ta có
23 23 1
47 46 2
=
24 24 1
45 48 2
=
Vậy
23 1 24 23 24
47 2 45 47 45
g) Ta có:
13 13 1
27 26 2
=
17 17 1
33 34 2
=
Vậy
13 1 17 13 17
27 2 33 27 33
Bài 8:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
So sánh hai phân số sau
a)
15
25
và
5
7
b)
13
60
và
27
100
c)
1993
1995
và
997
998
d)
47
15
và
29
35
e)
3
8
và
17
49
g)
43
47
và
29
35
i)
16
27
và
15
29
k)
15
59
và
24
47
.
Lời giải
a) Ta có:
5 5.3 15
7 7.3 21
==
.
15 15 15 5
.
25 21 25 7
b) Ta có
13 15 1
60 60 4
=
27 25 1
100 100 4
=
Vậy
13 1 27 13 27
60 4 100 60 100
c) Ta có:
1993 1995 1993 2
1.
1995 1995 1995 1995
−=−=
997 998 997 1
1
998 998 998 998
− = − =
1 2 2 1993 997
998 1996 1995 1995 998
=
d) Ta có:
47
47 15 1
15
29
29 35 1
35
29 47
1
35 15
. Vậy:
29 47
35 15
e) Ta có:
3 3.6 18
8 8.6 48
==
17 17 18
49 48 48
17 3
49 8
g) Ta có:
43 43.6 258
47 47.6 282
==
29 29.4 116
35 35.4 140
==
43 258 282 258 24
11
47 282 282 282 282
− = − = − =
29 116 140 116 24
11
35 140 140 140 140
− = − = − =
24 24 43 29
282 116 47 35
i) Ta có:
15 16 16
29 29 27
15 16
29 27
.
k) Ta có:
24 24 1
47 48 2
=
15 15 3 5 1
59 50 10 10 2
= =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy
15 1 24 15 24
59 2 47 59 47
.
Bài 9:
So sánh hai phân số:
a)
13
15
và
1333
1555
b)
42
43
và
58
59
.
Lời giải
a) Ta có:
13 13.111 1443
.
15 15.111 1665
==
1443 1665 1443 222
1
1665 1665 1665 1665
−=−=
1333 1555 1333 222
1
1555 1555 1555 1555
−=−=
222 222 13 1333
1665 1555 15 1555
b) Ta có:
42 1 58 1
1 ;1
43 43 59 59
− = − =
.
Vì
11
43 59
nên
42 58
43 59
.
Bài 10:
So sánh hai phân số sau
a)
13
15
và
23
25
b)
13
38
và
16
49
c)
23
28
và
25
49
d)
13
15
và
133
153
e)
15
21
và
153
213
Lời giải
a) Ta có:
13 15 13 2
1
15 15 15 15
−=−=
23 25 23 2
1
25 25 25 25
−=−=
Mà
2 2 13 23
15 25 15 25
.
b) Ta có:
13 13 1
38 39 3
=
16 16 1
49 48 3
=
Vậy
16 1 13
.
49 3 38
c) Ta có:
25 28 4 16 23
49 49 7 28 28
= =
.
Vậy
25 23
49 28
.
d) Ta có:
13 130 3 13 130 3 133
1.
15 150 3 15 150 3 153
+
= = =
+
Vậy
13 133
15 153
.
e) Ta có:
15 150 3 15 150 3 153
.
21 210 3 21 210 3 213
+
= =
+
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy
15 153
21 213
Bài 11:
So sánh các phân số sau với 1
a)
34.34
33.35
b)
1999.1999
1995.1995
c)
198519851985.198719871987
198619861986.198619861986
Lời giải
a) Ta có
22
2
34.34 34 34
1.
33.35 (34 1)(34 1) 34 1
= =
− + −
b) Ta có:
2
2
1999.1999 1999
1
1995.1995 1995
=
c) Ta có
2
198519851985.198719871987 1985.100010001.1987.100010001 1985.1987
198619861986.198619861986 1986.100010001.1986.100010001 1986
==
2
2
2
(1986 1)(1986 1)
1986
1986 1
1
1986
−+
=
−
=
Bài 12:
Không quy đồng mẫu hãy so sánh phân số sau bằng cách nhanh nhất:
a)
2012
2013
và
2013
2014
b)
1006
1007
và
2013
2015
c)
64
73
và
45
51
d)
`
2323 20132013
a
2424 20142014
v
Lời giải
a) Ta có: 1 -
2012
2013
=
1
2013
; 1 -
2013
2014
=
1
2014
.
Vì
1
2013
>
1
2014
nên
2012
2013
<
2013
2014
.
b) Ta thấy:
1006 1006 2 2012
1007 1007 2 2014
==
.
Ta có:
2012 2
1
2014 2014
−=
;
2013 2
1
2015 2015
−=
.
Vì
2
2014
>
2
2015
nên
2012 2013
2014 2015
hay
1006 2013
1007 2015
c) Ta thấy:
64
73
=
64 2 128
73 2 146
=
;
45
51
=
45 3 135
51 3 153
=
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Ta có:
128 18
1
146 146
−=
;
135 18
1.
153 153
−=
.
Vì
18 18
143 153
nên
128 135
146 153
hay
64 45
.
73 51
d) Ta thấy:
2323 23 101 23
2424 24 101 24
==
;
20132013 2013 10001 2013
20142014 2014 10001 2014
==
.
Ta có:
23 1
1
24 24
−=
;
2013 1
1.
2014 2014
−=
Vì
11
24 2014
nên
23 2013
24 2014
Vậy
2323 20132013
.
2424 20142014
Dạng 5: So sánh phần hơn (phần thừa) với đơn vị của các phân số.
I. Phương pháp giải.
* Phần hơn với đơn vị của phân số là hiệu giữa phân số đó với 1
Ví dụ: Tìm phần hơn với đơn vị của phân số
8
5
Ta lấy :
83
1
55
−=
Vậy phần hơn với đơn vị của phân số
8
5
là
3
5
* Sử dụng cách so sánh bằng phần hơn khi:
- Nhận thấy tất cả các phân số đều có tử số lớn hơn mẫu số (phân số lớn hơn 1) và hiệu của tử số với
mẫu số đều bằng nhau hoặc nhỏ thì ta tìm phần hơn với 1.
- Nhận thấy cả hai phân số đều có tử số lớn hơn mẩu số và nếu lấy tử số chia cho mầu số ở cả hai phân
số thì có thương bằng nhau. (ví dụ 5)
- Nhận thấy cả hai phân số đều có tử số bé hơn mẫu số và nếu lấy mẫu số chia cho tử số ở cả hai phân
số thì có thương bằng nhau. (ví dụ 6)
- Lưu ý:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
+ Trong hai phân số, phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn và ngược lại phân số nào
có phần hơn nhỏ hơn thì phân số đó nhỏ hơn.
* Các bước tiến hành:
+ Bước 1: Tìm phần hơn của hai phân số
+ Bước 2: So sánh hai phần hơn với nhau
+ Bước 3: Kết luận.
II. Bài toán.
Bài 1:
So sánh hai phân số
8
5
là
14
11
Hướng dẫn
Hai phân số
8
5
và
14
11
có đặc điểm:
+ Đều lớn hơn 1 vì có tử số lớn hơn mẫu số.
+ Tử số - mẫu số
3=
Vậy ta sẽ chọn cách So sánh phần hơn với đơn vị của hai phân số.
Lời giải
Ta có :
8 3 14 3
1 ; 1
5 8 11 11
− = − =
.
Vì
33
8 11
(hai phân số có cùng tử số, mẫu số có
8 11
).
Vậy
8 14
5 11
.
Bài 2:
So sánh:
2016
2012
và
2018
2014
Hướng dẫn:
Hai phân số
2016
2012
và
2018
2014
có đặc điểm:
+ Đều lớn hơn 1 vì có tử số lớn hơn mẫu số.
+ Tử số - mẫu số
4=
Vậy ta sẽ chọn cách so sánh phần hơn với đơn vị của hai phân số.
Lời giải
Ta có:
2016 4 2018 4
1 ; 1
2012 2012 2014 2014
− = − =
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vì
44
2012 2014
(hai phân số có cùng tử số, mẫu số có
2012 2014
)
Vậy
2016 2018
2012 2104
Bài 3:
So sánh hai phân số
43
14
và
10
3
.
Lời giải
Ta làm như sau:
Lấy tử số chia cho mẫu số:
43:14 3=
(dư 1)
10:3 3=
(dư 1 ).
Chọn phần nguyên của thương làm số chung (có 3).
Thực hiện phép trừ:
43 1 10 1
3 ; 3
14 14 3 3
− = − =
.
Vậy ta có:
43 1 10 1
3 ; 3
14 14 3 3
= + = +
Vì
11
3 14
nên
43 10
14 3
.
Bài 4:
So sánh hai phân số
77
76
và
84
83
.
Lời giải
Ta có
77 1 84 1
1 ; 1
76 76 83 83
= + = +
Vì
11
76 83
nên
77 84
76 83
Bài 5:
So sánh hai phân số
13
41
và
19
71
.
Lời giải
Ta làm như sau:
Lấy mẫu số chia cho tử số:
41:13 3=
(dư 2);
71:19 3=
(dư 14).
Chọn mẫu số của phân số chung bằng cách lấy phần nguyên của thương cộng
1:3 1 4+=
Thực hiện phép trừ:
13 1 11 19 1 5
;
41 4 164 71 4 284
− = − =
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Vậy ta có:
13 1 11 19 1 5
;
41 4 164 71 4 284
= + = +
.
Vì:
5 11 11
284 284 164
nên
19 13
71 41
.
Bài 6:
So sánh hai phân số
21
89
và
2003
8017
.
Lời giải
Ta nhận thấy hai phân số đã cho nếu lấy mẫu số chia cho tử số thì đều được thương là 4 và số dư là 5 .
Ta có:
21 89 2003 8017
1: ;1:
89 21 8017 2003
==
.
Mà
89 5 8017 5
4 ; 4
21 21 2003 2003
= + = +
.
Vì
55
21 2003
nên
89 8017
21 2003
.
Suy ra:
21 2003
89 8017
.
Bài 7:
Cho
2002
2003
10 1
A
10 1
+
=
+
và
2003
2004
10 1
B.
10 1
+
=
+
So sánh
A
và
B
.
Lời giải
2003
2003 2003
10 10 9
10 1
10 1 10 1
A
+
= = +
++
2004
2004 2004
10 10 9
10. 1
10 1 10 1
B
+
= = +
++
Vì
2003 2004
99
10 1 10 1
++
(cùng tử số, mẫu số càng lớn thì phân số càng nhỏ)
Nên
10. 10.AB
Hay:
AB
Bài 8:
So sánh các phân số sau
3535.232323
353535.2323
A =
;
3535
3534
B =
;
2323
2322
C =
Lời giải
Ta có:
3535.232323 35.101.23.10101
1
353535.2323 35.10101.23.101
A = = =
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
3535 1
1
3534 3534
B = = +
2323 1
1
2322 2322
C = = +
Vì
11
3534 2322
(cùng tử số, mẫu số càng lớn thì phân số càng nhỏ) nên
A B C
.
Bài 9:
So sánh các phân số sau
5.(11.13 22.26)
22.26 44.52
A
−
=
−
;
2
2
138 690
137 548
B
−
=
−
Lời giải
5.(11.13 22.26) 5.11.13.(1.1 2.2) 5 1
1
22.26 44.52 22.26.(1.1 2.2) 4 4
A
−−
= = = = +
−−
2
2
138 690 138.(138 5) 138 1
1
137 548 137.(137 4) 137 137
B
−−
= = = = +
−−
Vì
11
4 137
(cùng tử số, mẫu số càng lớn thì phân số càng nhỏ) nên
AB
Ta có:
5.(11.13 22.26)
22.26 44.52
A
−
=
−
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Dạng 6: So sánh một tổng hoặc một tích nhiều phân số với một phân số.
I. Phương pháp giải.
Bước 1: Tìm số chữ số của tổng.
Bước 2: Tách số cố định thành tổng các chữ số.
Bước 3: So sánh từng số của tổng với các chữ số vừa tách.
Bước 4: Kết luận
II. Bài toán.
Bài 1:
So sánh:
a)
1 1 1 1
101 102 199 200
+ ++ +
với 1 ;
b)
1 1 1 1
101 102 149 150
+ ++ +
với
1
3
;
c)
1 1 1 1
101 102 199 200
+ ++ +
với
7
12
Lời giải
a) Từ
1
101
tới
1
200
có tất cả 100 chữ số.
Mà
(
1 1 1
1
100 100 100
= + ++
có 100 chữ số
1
100
Vì
1 1 1 1 1 1
; ; ;
101 100 102 100 200 100
Nên:
1 1 1 1 1 1 1
101 102 199 200 100 100 100
+ + + + + ++
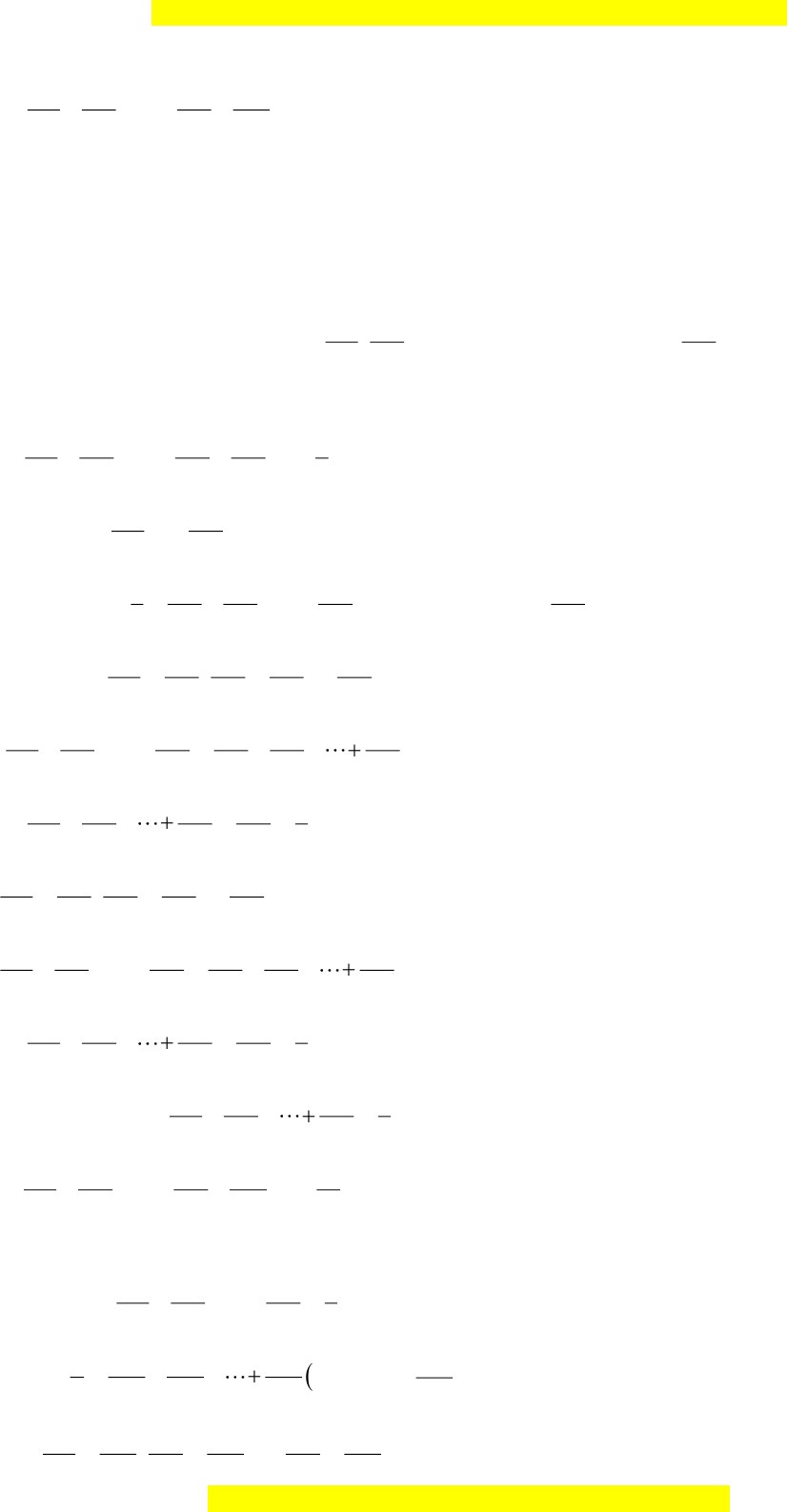
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
1 1 1 1
1
101 102 199 200
→ + ++ +
Kết luận: Vậy nếu gặp dạng so sánh như trên (dấu hiệu so sánh 1 số với tổng dãy số), các em thực
hiện theo các bước:
Bước 1: Tìm số chữ số của tổng (ví dụ bài toán trên là 100 chữ số)
Bước 2: Tách số cố định thành tổng các chữ số (ví dụ trên là tách 1 thành tổng 100 chữ số)
Bước 3: So sánh từng số của tổng
11
; ;..
101 102
với các chữ số vừa tách
1
100
Bước 4: Kết luận
b)
1 1 1 1
101 102 149 150
+ ++ +
với
1
3
;
Bước 1: Từ
1
101
tới
1
150
có tất cả 50 chữ số.
Bước 2: Tách
1 1 1 1
3 150 150 150
= + ++
(có tất cả 50 chữ số
1
150
)
Bước 3: Vì
1 1 1 1 1
; ; 150
101 150 102 150 149
1 1 1 1 1 1
101 102 150 150 150 150
+ ++ + + +
1 1 1 50 1
101 102 150 150 3
→ + + + =
1 1 1 1 1
; ; 150
101 150 102 150 149
1 1 1 1 1 1
101 102 150 150 150 150
+ ++ + + +
1 1 1 50 1
101 102 150 150 3
→ + + + =
Bước 4: Kết luận:
1 1 1 1
101 102 150 3
+ + +
c)
1 1 1 1
101 102 199 200
+ ++ +
với
7
12
Phần này khó hơn 2 phần a và
b
một chút, chúng ta sẽ phải kết hợp:
Chúng ta có
1 1 1 1
101 102 150 3
+ ++
(1)
Lại có:
(
1 1 1 1
50
4 200 200 200
= + + +
chữ số
1
200
Mà:
1 1 1 1 1 1
; ; ;
151 200 152 200 199 200
Nên:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
1 1 1 1
151 152 200 4
+ ++
Cộng (1) và (2) chúng ta được:
1 1 1 1 1 3 4 7
101 102 200 3 4 12 12
+
+ ++ + = =
Kết luận:
1 1 1 7
101 102 200 12
+ ++
Bài 2:
Cho tổng
1 1 1
:
31 32 60
S = + ++
. Chứng minh:
34
55
S
Lời giải
1 1 1 1 1 1 1 1 1
31 32 40 41 42 50 51 52 60
S
= + ++ + + ++ + + ++
1 1 1 1 1 1 1 1 1
30 30 30 40 40 40 50 50 50
S
+ ++ + + ++ + + ++
hay
10 10 10
30 40 50
S + +
suy ra
47 48
60 60
S
Vậy
4
5
S
(1).
Mặt khác:
1 1 1 1 1 1 1 1 1
40 40 40 50 50 50 60 60 60
S
+ ++ + + ++ + + ++
10 10 10
40 50 60
S + +
37 36
60 60
S
3
(2)
5
S
Từ (1) và (2) suy ra đpcm.
Bài 3:
So sánh
1 3 5 9999
A
2 4 6 10000
=
với
1
B
100
=
Lời giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đặt
2 4 6 8 10000
3 5 7 9 10001
C =
So sánh từng số của
A
với của
C
ta thấy:
1 2 3 4
;
2 3 4 5
và
9999 10000
10000 10001
Vậy
AC
1 3 5 9999 2 4 6 10000
.
2 4 6 10000 3 5 7 10001
A A AC
→ =
2
1 2 3 4 5 9999 10000
2 3 4 5 6 10000 10001
A
→
(Rút gọn tử và mẫu lần lượt).
2
1
10001
A→
mà
11
10001 10000
(mẫu càng lớn phân số càng nhỏ)
2
2
11
10000 100
A
→ =
1
100
AB→ =
Kết luận:
AB
Bài 4:
Chứng minh rằng:
1 1 1 1 1 1 7
..
41 42 43 78 79 80 12
+ + + + + +
Lời giải
Ta thấy:
1
41
đến
1
80
có 40 phân số.
Vậy
1 1 1 1 1 1
..
41 42 43 78 79 80
+ + + + + +
1 1 1 1 1 1 1 1 1 1
.. ..
41 42 43 59 60 61 62 63 79 80
= + + + + + + + + + + +
(1)
Vì
1 1 1
.
41 42 60
và
1 1 1
61 62 80
(2)
Ta có
1 1 1 1 1 1 1 1 1
..
60 60 60 60 80 80 80 80 80
= + + + + + + + + + +
20 20 1 1 4 3 7
60 80 3 4 12 12
+
= + = + = =
(3)
Từ (1), (2), (3) Suy ra:
1 1 1 1 1 1 7
41 42 43 78 79 80 12
+ + ++ + +
Bài 5:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
So sánh
2 2 2 2
1 1 1 1
...
232 n
+ + + +
và 1
Lời giải
2
11
1
22
−
2
1 1 1
3 2 3
−
2
1 1 1
4 4 3
−
…
…
2
1 1 1 1
( 1) 1n n n n n
= −
−−
2 2 2 2
1 1 1 1 1
... 1 1
234 nn
+ + + + −
Vậy
2 2 2 2
1 1 1 1
... 1
234 n
+ + + +
Bài 6:
So sánh
2 3 99
1 1 1 1
...
3 3 3 3
A = + + + +
với
1
2
Lời giải
Ta có:
2 3 99
1 1 1 1
3 3( ... )
3 3 3 3
A = + + + +
=
2 3 98
1 1 1 1
(1 ... )
3 3 3 3
+ + + + +
Suy ra
99
1
31
3
AA− = −
99
1
21
3
A =−
99
1 1 1
2 2.3 2
A = −
Vậy
2 3 99
1 1 1 1 1
...
3 3 3 3 2
A = + + + +
Bài 7:
Cho
1 3 5 99
. . ...
2 4 6 100
M =
và
2 4 6 100
. . ...
3 5 7 101
N =
a) Chứng minh:
MN
b) Tìm tích
.MN
c) Chứng minh:
1
10
M
Lời giải
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Nhận xét M và N đều có 45 thừa số:
a) Và
1 2 3 4 5 6 99 100
; ; ;...
2 3 4 5 6 7 100 101
nên M < N
b) Tích
1 3 5 99 2 4 6 100 1
. . . ... . . . ...
2 4 6 100 3 5 7 101 101
MN
==
c)Vì
1
.
101
MN=
mà
MN
nên ta suy ra được:
11
.
101 100
MM
Tức là M.M <
1
10
.
1
10
M <
1
10
Dạng 7: Dạng bài tập phối hợp nhiều phương pháp
I. Phương pháp giải.
* Phương pháp so sánh hai phân số bằng cách "nhân thêm cùng một số vào hai phân số"
- Ta sử dụng phương pháp nhân thêm cùng một số vào hai phân số khi nhận thấy tử số của hai phân số
đều bé hơn mẫu số và nểu lấy mẫu số chia cho tử số thì có thương và số dư bằng nhau. Khi đó ta nhân
cả hai phân số với cùng một số tự nhiên (là phần nguyên của thương) để đưa về dạng so sánh "phần
bù"
Bài 1:
So sánh hai phân số
11
52
và
17
76
.
Lời giải
Ta nhận thấy hai phân số đã cho nếu lấy mẫu số chia cho tử số thì đều được thương là 4 và số dư là 8
nên ta nhân cả hai phân số với 4 .
Ta có:
11 44
4;
52 52
=
17 68 44 8
4 1 ;
76 76 52 52
= − =
68 8
1
76 76
−=
Vì
88
52 76
nên
44 68
52 76
hay
11 17
52 76
.
* Phương pháp so sánh hai phân số bằng cách "phép chia hai phân số"
- Phương pháp này được sử dụng dựa vào nhận xét: "Trong phép chia, nếu số bị chia lớn hơn số chia
thì được thương lớn hơn 1, nếu số bi chia bé hơn số chia thì được thương nhỏ hơn 1".
- Ta sử dụng phương pháp "chia hai phân số" khi nhận thấy tử số và mẫu số của hai phân số là những
số có giá trị không quá lớn, không mất nhiều thời gian khi thực hiện phép nhân ở tử số và mẫu số.
Bài 2:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
So sánh hai phân số
2
23
và
9
41
.
Lời giải
Ta có:
2 9 2 41 82
:.
23 41 23 9 207
= =
Vì
82
1
207
nên
29
23 41
.
Bài 3:
So sánh hai phân số
8
9
10 1
A
10 1
+
=
+
và
9
10
10 1
B
10 1
+
=
+
.
Lời giải
Cách 1:
B
là phân số nhỏ hơn 1 . Nếu cộng cùng một số nguyên dương vào tử và mẫu của
B
thì giá
trị của
B
tăng thêm. Do dó
( )
( )
8
9 9 9 8
10 10 10 9
9
10 10 1
10 1 10 1 9 10 10 10 1
BA
10 1 10 1 9 10 10 10 1
10 10 1
+
+ + + + +
= = = = =
+ + + + +
+
Vậy
BA
.
Cách 2. (sau khi học phép nhân phân sô)
( )
( )
8
9
9 9 9
9
10
10 10 10
10 10 1
10 10 9
10 A 1
10 1 10 1 10 1
10 10 1
10 10 9
10 B 1
10 1 10 1 10 1
+
+
= = = +
+ + +
+
+
= = = +
+ + +
Ta thấy
9 10
99
10 1 10 1
++
(so sánh hai phân số cùng tử) nên
10 A 10 B
.
Do đó
AB
.
Bài 4:
So sánh
2003
2004
2003 1
A
2003 1
+
=
+
và
2002
2003
2003 1
B
2003 1
+
=
+
Lời giải
Nhận thấy tử và mẫu có số mũ lớn và đều cách nhau là 2003, nên:
2003.A
( )
2003
2004
2004 2004 2004
2003 2003 1
2003 2003 2002
1
2003 1 2003 1 2003 1
+
+
= = = +
+ + +
2003.
( )
2002
2003
2003 2003 2003
2003 2003 1
2003 2003 2002
B1
2003 1 2003 1 2003 1
+
+
= = = +
+ + +
Vì
2004 2003
2002 2002
2003 1 2003 1
++
(do cùng tử mà mẫu càng lớn phân số càng bé)
Nên
A B
.
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 5:
a) So sánh phân số
15
301
với
25
490
b) So sánh tổng
2 3 2007
1 2 3 2007
... ...
2 2 2 2 2
n
n
S = + + + + + +
với
*
2 ( )nN
Lời giải
a)
15 15 1 25 25
.
301 300 20 500 499
= =
Vậy
15 25
301 499
b) So sánh tổng
2 3 2007
1 2 3 2007
... ...
2 2 2 2 2
n
n
S = + + + + + +
với
*
2 ( )nN
Với
n2
ta có:
n1
n n 1 n 2
2 2 2
nn+
++
=−
.
Từ đó ta có:
2 2 3 2006 2007 2007
1 3 4 4 5 2008 2009 2009
S .. 2 2.
2 2 2 2 2 2 2 2
= + − + − + + − = −
Vậy
S2
Bài 6:
Cho
2002
2003
10 1
A
10 1
+
=
+
và
2003
2004
10 1
B.
10 1
+
=
+
So sánh
A
và
B
.
Lời giải
10.
2003
2003 2003
10 10 9
A1
10 1 10 1
+
= = +
++
2004
2004 2004
10 10 9
10.B 1
10 1 10 1
+
= = +
++
Vì
2003 2004
99
10 1 10 1
++
(cùng tử số, mẫu số càng lớn thì phân số càng nhỏ)
Nên
10.A 10.B
Hay:
AB
Bài 7:
So sánh hai phân số
13
41
và
19
71
.
Lời giải
Lấy mẫu số chia cho tử số:
41:13 3=
(dư 2)
71:19 3=
dư 14).
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Chọn mẫu số của phân số chung bằng cách lấy phần nguyên của thương cộng
1:3 1 4+=
(có
1
4
)
Thực hiện phép trừ:
13 1 11 19 1 5
;
41 4 164 71 4 284
− = − =
.
Vậy ta có:
13 1 11
41 4 164
19 1 5
71 4 284
=+
=+
.
Vì
5 11 11
284 284 164
nên
19 13
71 41
.
Bài 8:
Cho
199919991999
20002002000
A =
và
1999
2000
B =
. Hãy so sánh
A
và
B
.
Lời giải
199919991999 1999000000 19990000 1999
20002002000 2000000000 20000000 2000
A
++
==
++
( )
1999 100000000 10000 1
2000(100000000 10000 1)
++
=
++
1999.100010001
2000.100010001
=
1999
2000
B==
Vậy
AB=
Bài 9:
a) Chứng minh rằng các phân số sau bằng nhau:
25 2525 252525
;;
53 5353 535353
b) Không quy đồng mẫu hãy so sánh phân số sau
37
67
và
377
677
Lời giải
a) Ta có:
2525 25.101 25
5353 53.101 53
==
252525 25.10101 25
535353 53.10101 53
==
Vậy
25 2525 252525
53 5353 535353
==
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
b)
300 300
670 677
mà
300 30 30 300
670 67 67 677
=
(1)
Ta có:
377 37
677 67
37 30
1
67 67
−=
và
377 300
1
677 677
−=
(2)
Từ (1) và (2) suy ra
377 37
677 67
Bài 10:
So sánh
11
12
10 1
10 1
A
−
=
−
và
10
11
10 1
10 1
B
+
=
+
Lời giải
Ta có :
11
12
10 1
1
10 1
A
−
=
−
(vì tử nhỏ hơn mẫu)
11 11 11 10
12 12 12 11
10 1 (10 1) 11 10 10 10 1
10 1 (10 1) 11 10 10 10 1
AB
− − + + +
= = = =
− − + + +
Vậy A < B .
Bài 11:
So sánh
2004 2005
2005 2006
M =+
và
2004 2005
2005 2006
N
+
=
+
Lời giải
Ta có
2004 2004
2005 2005 2006
+
2005 2005
2006 2005 2006
+
Cộng vế với vế ta được
MN
Bài 12:
So sánh
37
39
và
3737
3939
Lời giải
37 3700 3700 37 3737
39 3900 3900 39 3939
+
= = =
+
(áp dụng tính chất
.
a c a c
b d b d
+
==
+
)
Bài 13:
Cho
, , *a b m N
. Hãy so sánh
am
bm
+
+
và
a
b
Lời giải
Xét các trường hợp
1
a
b
=
;
1
a
b
;
1
a
b
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a) Trường hợp
1
a
ab
b
= =
thì
1
a m a
b m b
+
==
+
b) Trường hợp
1
a
a b a m b m
b
+ +
am
bm
+
+
có “phần bù” tới 1 là
ba
bm
−
+
a
b
có “phần bù” tới 1 là
ba
b
−
, vì
b a b a
b m b
−−
+
nên
a m a
b m b
+
+
.
c) Trường hợp
1
a
a b a m b m
b
+ +
am
bm
+
+
có “phần thừa” tới 1 là
ba
bm
−
+
a
b
có “phần thừa” tới 1 là
ab
b
−
, vì
a b a b
b m b
−−
+
nên
a m a
b m b
+
+
.
Bài 14:
Cho tổng
1 1 1
...
31 32 60
S = + + +
. Chứng minh
34
55
S
Lời giải
Tổng S có 30 số hạng, cứ nhóm 10 số hạng thành một nhóm. Giữ nguyên tử, nếu thay mẫu bằng một
mẫu khác lớn hơn thì giá trị của phân số sẽ giảm đi. Ngược lại, nếu thay mẫu bằng một mẫu khác nhỏ
hơn thì giá trị của phân số sẽ tăng lên.
Ta có
1 1 1 1 1 1 1 1 1
... ... ...
31 32 40 41 42 50 51 52 60
S
= + + + + + + + + + + +
1 1 1 1 1 1 1 1 1
... ... ...
30 30 30 40 40 40 50 50 50
S
+ + + + + + + + + + +
hay
10 10 10
30 40 50
S + +
Tức là:
47 48
60 60
S
Vậy
4
5
S
(1)
Mặt khác:
1 1 1 1 1 1 1 1 1
... ... ...
40 40 40 50 50 50 60 60 60
S
+ + + + + + + + + + +
10 10 10
40 50 60
S + +
Tức là :
37 36
60 60
S
vậy
3
5
S
(2).
Từ (1) và (2) suy ra
34
55
S
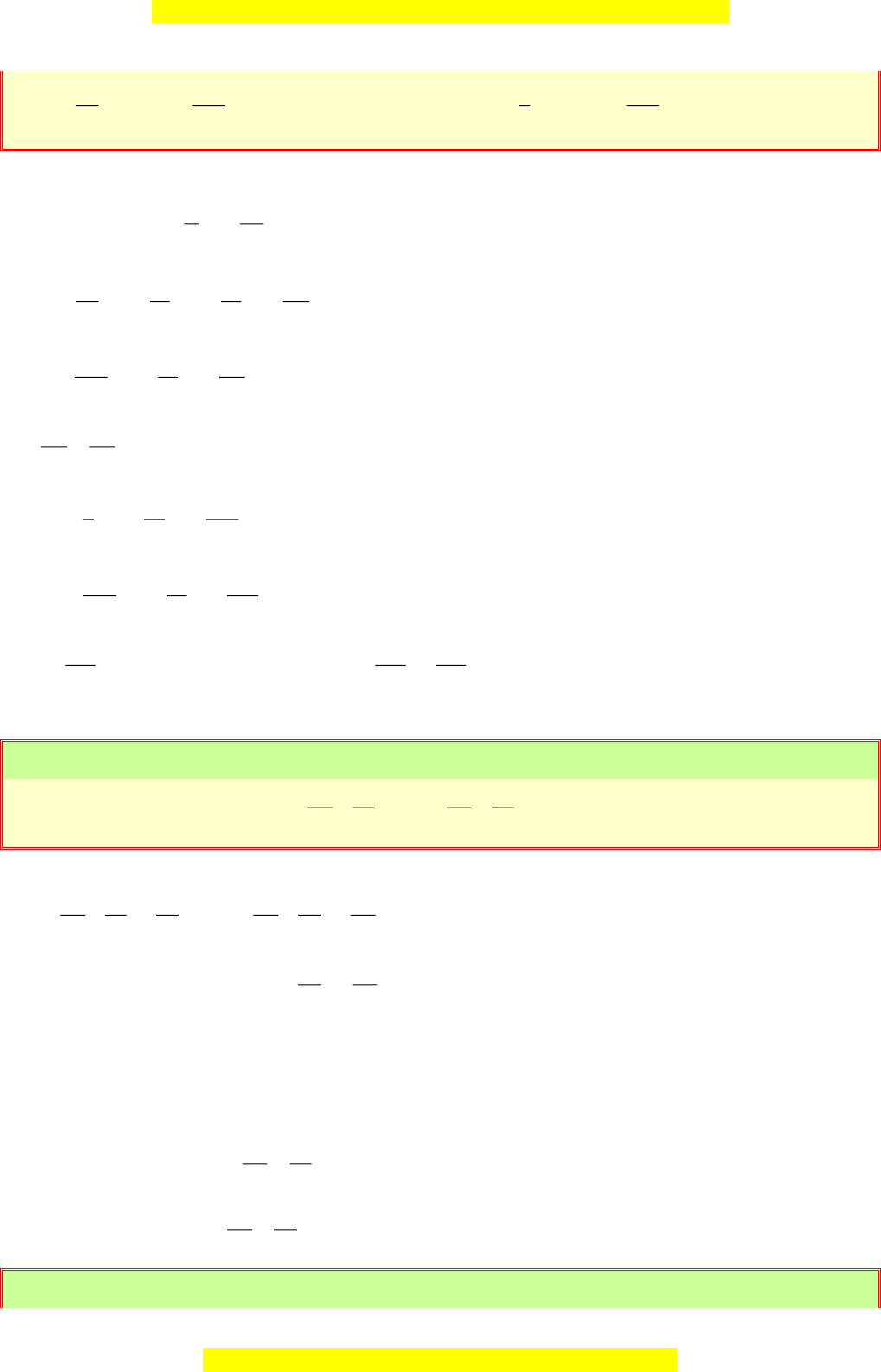
Bài 15:
So sánh
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
a)
7
1
80
A
=
và
6
1
;
243
B
=
b)
5
3
8
C
=
và
3
5
243
D
=
Lời giải
Áp dụng công thức
( )
.
&
n
n
n
m m n
n
xx
xx
yy
==
a)
7 7 7
4 28
1 1 1 1
80 81 3 3
A
= = =
66
5 30
1 1 1
;
243 3 3
B
= = =
Vì
28 30
11
33
nên
AB
b)
55
3 15
3 3 243
8 2 2
C
= = =
33
5 15
5 5 125
.
243 3 3
D
= = =
Chọn
15
125
2
làm phân số trung gian, so sánh
15
125
2
>
15
125
3
Vậy C > D.
Bài 16:
Cho
*
,,a m n N
. Hãy so sánh
10 10
mn
A
aa
=+
và
11 9
mn
B
aa
=+
Lời giải
10 9 1
m n n
A
a a a
= + +
;
10 9 1
m n m
B
a a a
= + +
Muốn so sánh A và B ,ta so sánh
1
n
a
và
1
m
a
bằng cách so sánh các trường hợp sau:
a) Với
1a =
thì
mn
a a A B= =
b) Với a
0:
- Nếu m= n thì a
m
= a
n
A=B
- Nếu m< n thì
11
mn
mn
a a A B
aa
- Nếu m > n thì
11
mn
mn
a a A B
aa
Bài 17:
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
So sánh P và Q, biết rằng
31 32 33 60
. . ....
2 2 2 2
P =
và
1.3.5.7....59Q =
Lời giải
30 30
31 32 33 60 31.32.33....60 (31.32.33.60).(1.2.3....30)
. . ....
2 2 2 2 2 2 .(1.2.3....30)
(1.3.5....59).(2.4.6....60)
1.3.5....59
2.4.6....60
P
Q
= = =
= = =
Vậy
PQ=
Bài 18:
Sắp xếp các phân số
47 17 27 37
; ; ;
223 98 148 183
theo thứ tự tăng dần
Lời giải
Xét các phân số nghịch đảo
223 98 148 183
; ; ;
47 17 27 37
,
Nếu đổi ra hỗn số là
35 13 13 35
4 ;5 ;5 ;4
47 17 27 37
Ta thấy:
13 13 35 35
5 5 4 4
17 27 37 47
Suy ra
`
17 27 37 47
()
98 148 183 223
a c b d
vi
b d a c
Bài 19:
So sánh P và Q, biết rằng
2010 2011 2012
2011 2012 2013
P = + +
và
2010 2011 2012
2011 2012 2013
Q
++
=
++
Lời giải
2010 2011 2012
2011 2012 2013
Q
++
=
++
2010 2011 2012
2011 2012 2013 2011 2012 2013 2011 2012 2013
= + +
+ + + + + +
Vì
2010 2010
2011 2012 2013 2011
++
2011 2011
2011 2012 2013 2012
++
2012 2012
2011 2012 2013 2013
++
Cộng vế với vế ta có:
2010 2011 2012 2010 2011 2012
2011 2012 2013 2011 2012 2013 2011 2012 2013 2011 2012 2013
+ + + +
+ + + + + +
Vậy:
QP
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Bài 20:
So sánh
A
và
B
, biết rằng
2005
2006
2005 1
2005 1
A
+
=
+
và
2004
2005
2005 1
2005 1
B
+
=
+
Lời giải
2005 2005 2004 2004
2006 2006 2005 2005
2005 1 2005 1 2004 2005.(2005 1) 2005 1
.
2005 1 2005 1 2004 2005.(2005 1) 2005 1
AB
+ + + + +
= = == =
+ + + + +
Vậy
A
<
B
.
Bài 21:
Hãy so sánh hai phân số
1999
2000
và
19992000
20002000
bằng tất cả các cách có thể được
Lời giải
Cách 1: Quy đồng mẫu số rồi so sánh tử.
Mẫu chung là 20002000
Ta có:
1999 19991999
2000 20002000
=
; giữ nguyên
19992000
20002000
Vì
19991999 19992000
20002000 20002000
Nên
1999 19992000
2000 20002000
Cách 2:
1999 19991999 19992000
2000 20002000 20002000
=
Vậy
1999 19992000
2000 20002000
Cách 3:
1999 1 19992000 10000
1
2000 2000 20002000 20002000
+ = + =
Vậy
1999 19992000
2000 20002000
..
Nhắn tin Zalo