ệ xem ể chi ti t ế (có l i ờ gi i ả ) SỞ GIÁO D C Ụ VÀ ĐÀO T O Ạ Đ Ề THI TUY N Ể SINH VÀO L P Ớ 10 THPT NAM Đ N Ị H NĂM HỌC 2019-2020 Bài thi: Toán Đ C Ề HÍNH TH C Ứ Th i ờ gian làm bài:120 phút Phần I. Tr c nghi ắ m ệ (2,0 đi m
ể ) Hãy ch n ph ọ ư ng án t ơ r l ả i ờ đúng và vi t ế ch cái ữ đ ng t ứ rư c ph ớ ư ng
ơ án đó vào bài làm. Câu 1. Tìm t t
ấ cả các giá tr ị m đ hàm ể số y
1 m x m 1đồng bi n t ế rên Câu 2. Phư ng ơ trình 2 x 2x 1 0
có hai nghiệm x , x . x x 1 2 Tính 1 2 A. x x 2 x x 1 x x 2 x x 1 1 2 B. 1 2 C. 1 2 D. 1 2 2 Câu 3. Cho đi m
ể M x ; y y 3x x 2. y M M thu c đ ộ ồ th ị . Bi t ế M Tính M A. y 6 y y y M B. 6 M C. 12 M D. 12 M x y 2 Câu 4. Hệ phư ng
ơ trình 3x y 1 có bao nhiêu nghi m ệ A. 0 B. 1 C. 2 D. Vô số Câu 5. V i
ớ các số a,b th a
ỏ mãn a 0,b 0 thì bi u t ể h c ứ a ab b ng: ằ 2 3 2 3 A. a b B. a b C. a b D. a b
Câu 6. Cho tam giác ABC vuông t i ạ A có AB 3 cm, AC 4 c . m Tính đ dài ộ đư ng cao ờ AH c a ủ tam giác ABC 12 5 12 7 AH cm AH cm AH cm AH cm A. 7 B. 2 C. 5 D. 2 Câu 7. Cho đư ng t ờ
ròn tâm O bán kính R 2 cm và đư ng t ờ
ròn tâm O ' bán kính R' 3 c . m Bi t ế OO' 6 c . m Số ti p t ế uy n chung ế c a hai ủ đư ng ờ tròn đã cho là: A. 1 B. 2 C. 3 D. 4 Câu 8. M t ộ qu bóng hì ả nh cầu có đư ng ờ kính b ng ằ 4c . m Th t ể ích qu bóng l ả à: 32 32 256 256 3 cm 3 cm 3 cm 3 cm A. 3 B. 3 C. D. 3 Phần II. T l ự u n ( ậ 8,0 đi m ể ) Câu 1. (1,5 đi m ể ) a) Rút g n bi ọ u t ể h c
ứ A 3 2 2 3 2 2 2 1 6 . a 3 1 b) Ch ng ứ minh r ng: ằ a 3
a 3 a 9 (v i ớ a 0 và a 9 ) 2 Câu 2. (1,5 đi m ể ) Cho phư ng
ơ trình x m 2 x 6 0 (1) v i ớ m là tham số a) Gi i ả phư ng t ơ rình (1) v i ớ m 0 M i
ọ thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
ệ xem ể chi ti t ế (có l i ờ gi i ả ) b) Ch ng ứ minh r ng v ằ i ớ m i ọ giá tr c ị a ủ m phư ng t ơ rình (1) luôn có hai nghi m ệ phân biệt c) G i ọ x , x 1 1 2 là hai nghi m ệ c a ph ủ ư ng ơ trình .Tìm t t ấ c gi ả á tr c ị a ủ m đ ể 2
x xy y 7 0 2
x xy 2 y 4 x 1 Câu 3. (1,0 đi m ể ) Gi i ả h ph ệ ư ng t ơ rình Câu 4. (3,0 đi m ể ) Qua đi m ể A n m ằ ngoài đư ng t ờ ròn (O) v hai ẽ ti p t ế uy n ế AB, AC c a ủ đư ng t ờ
ròn ( B,C là hai ti p đi ế m ể ). G i ọ E là trung đi m ể c a ủ đo n
ạ AC, F là giao đi m ể th hai ứ c a ủ EB v i ớ đư ng t ờ ròn (O). a) Ch ng ứ minh : t gi ứ ác ABOC là t gi ứ ác n i ộ ti p, t ế
am giác CEF đồng d ng ạ v i ớ tam giác BEC. b) G i ọ K là giao đi m ể th hai ứ c a đ ủ ư ng ờ th ng ẳ AF v i ớ đư ng ờ tròn (O). Ch ng ứ
minh BF.CK BK.CF c) Ch ng ứ minh AE là ti p t ế uy n c ế a đ ủ ư ng ờ tròn ngo i ạ ti p t ế am giác ABF 3 3 3 Câu 5. (1,0 đi m
ể ) Xét các số x, y, z thay đ i ổ th a
ỏ mãn x y z 3xyz 2 .Tìm giá 1
P x y z2 4 2 2 2
x y z xy yz zx trị nh nh ỏ t ấ c a ủ bi u t ể h c: ứ 2 M i
ọ thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
ệ xem ể chi ti t ế (có l i ờ gi i ả ) ĐÁP ÁN I. Phần tr c ngh ắ i m ệ 1B 2A 3C 4B 5D 6C 7D 8C II. Phần t l ự u n ậ Câu 1. a A 2 2 ) 3 2 2 3 2 2 2 1 2 1 2 1 2
1 2 1 2 1 2 2 1 6 . a 3 a 3
a 3 a 9 a 3 6 a 3 2 2 1 (df ) cm b) Ta có: a 3 a 3 a 3 Câu 2. a) V i ớ m 0 , ta có 1 tr t ở hành 2 x 2x 6 0 ' 7 0 phư ng ơ trình có hai nghi m
ệ x 1 7, x 1 7 1 2
b) Ta có ac 6 0 nên v i ớ m i ọ giá trị c a ủ m phư ng t ơ rình đã cho luôn có hai nghiệm phân bi t ệ x x m 2 1 2 2
, x m 2 2 x 6 0
x m 2 x 6 2 1 2 2 c) Ta có: x x 6 1 2 2
Khi đó x x x m 2 x 16
m 2 x 6 x x m 2 x 16 2 1 2 1 2 1 2 1 m 0
m 2 x x x x 1
0 m 2 2 6 10 m 2 2 4 1 2 1 2 m 4 2
x xy y 7 0 (1) 2
x xy 2 y 4 x 1 (2) Câu 3. Gi i ả h ph ệ ư ng t ơ rình M i
ọ thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
ệ xem ể chi ti t ế (có l i ờ gi i ả ) x
x 2 2 2
2 y x 2 0
x 2 x 2 y 0 Ta có: y 2 x V i ớ x 2 , ta có 1 tr t
ở hành 4 2y y 7 0 y 3 V i ớ y 2 x, ta có: x 1 y 3 2 x x 2 x 2 2 x 7 0 2x 3x 5 0 5 1 x y 1 tr t ở hành 2 2 5 1 ; x y
2; 3 ; 1;3 ; ; V y ậ h có nghi ệ m ệ 2 2 Câu 4. a) Ta có AB là ti p t ế uy n c ế a ủ đư ng t ờ ròn (O) nên 0 ABO 9 0 Tư ng t ơ ự 0 ACO 9 0 M i
ọ thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đề thi vào 10 môn Toán tỉnh Nam Định năm 2020
500
250 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ 63 đề thi vào 10 môn Toán hệ không chuyên năm 2020 nhằm giúp Giáo viên có thêm tài liệu tham khảo đề luyện thi Toán ôn luyện
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(500 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Ôn vào 10
Xem thêmTài liệu bộ mới nhất

Đây là b nả xem thử, vui lòng mua tài li u đ xem chi ti t (có l i gi i)ệ ể ế ờ ả
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
NAM Đ NHỊ
Đ CHÍNH TH C Ề Ứ
Đ THI TUY N SINH VÀO L P 10 THPTỀ Ể Ớ
NĂM H C 2019-2020Ọ
Bài thi: Toán
Th i gian làm bài:120 phút ờ
Ph n I. Tr c nghi m (2,0 đi m) ầ ắ ệ ể Hãy ch n ph ng án tr l i đúng và vi t ch cái ọ ươ ả ờ ế ữ
đ ng tr c ph ng án đó vào bài làm.ứ ướ ươ
Câu 1. Tìm t t c các giá tr ấ ả ị
m
đ hàm s ể ố
1 1y m x m
đ ng bi n trên ồ ế
Câu 2. Ph ng trình ươ
2
2 1 0x x
có hai nghi m ệ
1 2
, .x x
Tính
1 2
x x
A.
1 2
2x x
B.
1 2
1x x
C.
1 2
2x x
D.
1 2
1x x
Câu 3. Cho đi m ể
;
M M
M x y
thu c đ th ộ ồ ị
2
3y x
. Bi t ế
2.
M
x
Tính
M
y
A.
6
M
y
B.
6
M
y
C.
12
M
y
D.
12
M
y
Câu 4. H ph ng trình ệ ươ
2
3 1
x y
x y
có bao nhiêu nghi mệ
A.
0
B. 1 C. 2 D. Vô số
Câu 5. V i các s ớ ố
,a b
th a mãn ỏ
0, 0a b
thì bi u th c ể ứ
a ab
b ng:ằ
A.
2
a b
B.
3
a b
C.
2
a b
D.
3
a b
Câu 6. Cho tam giác
ABC
vuông t i A có ạ
3 , 4 .AB cm AC cm
Tính đ dài đ ng caoộ ườ
AH
c a tam giác ủ
ABC
A.
12
7
AH cm
B.
5
2
AH cm
C.
12
5
AH cm
D.
7
2
AH cm
Câu 7. Cho đ ng tròn tâm O bán kính ườ
2R cm
và đ ng tròn tâm ườ
'O
bán kính
' 3 .R cm
Bi t ế
' 6 .OO cm
S ti p tuy n chung c a hai đ ng tròn đã cho là:ố ế ế ủ ườ
A. 1 B. 2 C. 3 D. 4
Câu 8. M t qu bóng hình c u có đ ng kính b ng ộ ả ầ ườ ằ
4 .cm
Th tích qu bóng là:ể ả
A.
3
32
3
cm
B.
3
32
3
cm
C.
3
256
cm
D.
3
256
3
cm
Ph n II. T lu n (8,0 đi m)ầ ự ậ ể
Câu 1. (1,5 đi m) ể
a) Rút g n bi u th c ọ ể ứ
3 2 2 3 2 2A
b) Ch ng minh r ng:ứ ằ
2 1 6
. 3 1
9
3 3
a
a
a a
(v i ớ
0a
và
9)a
Câu 2. (1,5 đi m) ể Cho ph ng trình ươ
2
2 6 0 (1)x m x
v i ớ
m
là tham số
a) Gi i ph ng trình (1) v i ả ươ ớ
0m
M iọ th c m c vui lòng xin liên hắ ắ ệ hotline: 084 283 45 85

Đây là b nả xem thử, vui lòng mua tài li u đ xem chi ti t (có l i gi i)ệ ể ế ờ ả
b) Ch ng minh r ng v i m i giá tr c a ứ ằ ớ ọ ị ủ
m
ph ng trình (1) luôn có hai nghi m ươ ệ
phân bi t ệ
c) G i ọ
1 2
,x x
là hai nghi m c a ph ng trình ệ ủ ươ
1
.Tìm t t c giá tr c a ấ ả ị ủ
m
đ ể
Câu 3. (1,0 đi m) ể Gi i h ph ng trình ả ệ ươ
2
2
7 0
2 4 1
x xy y
x xy y x
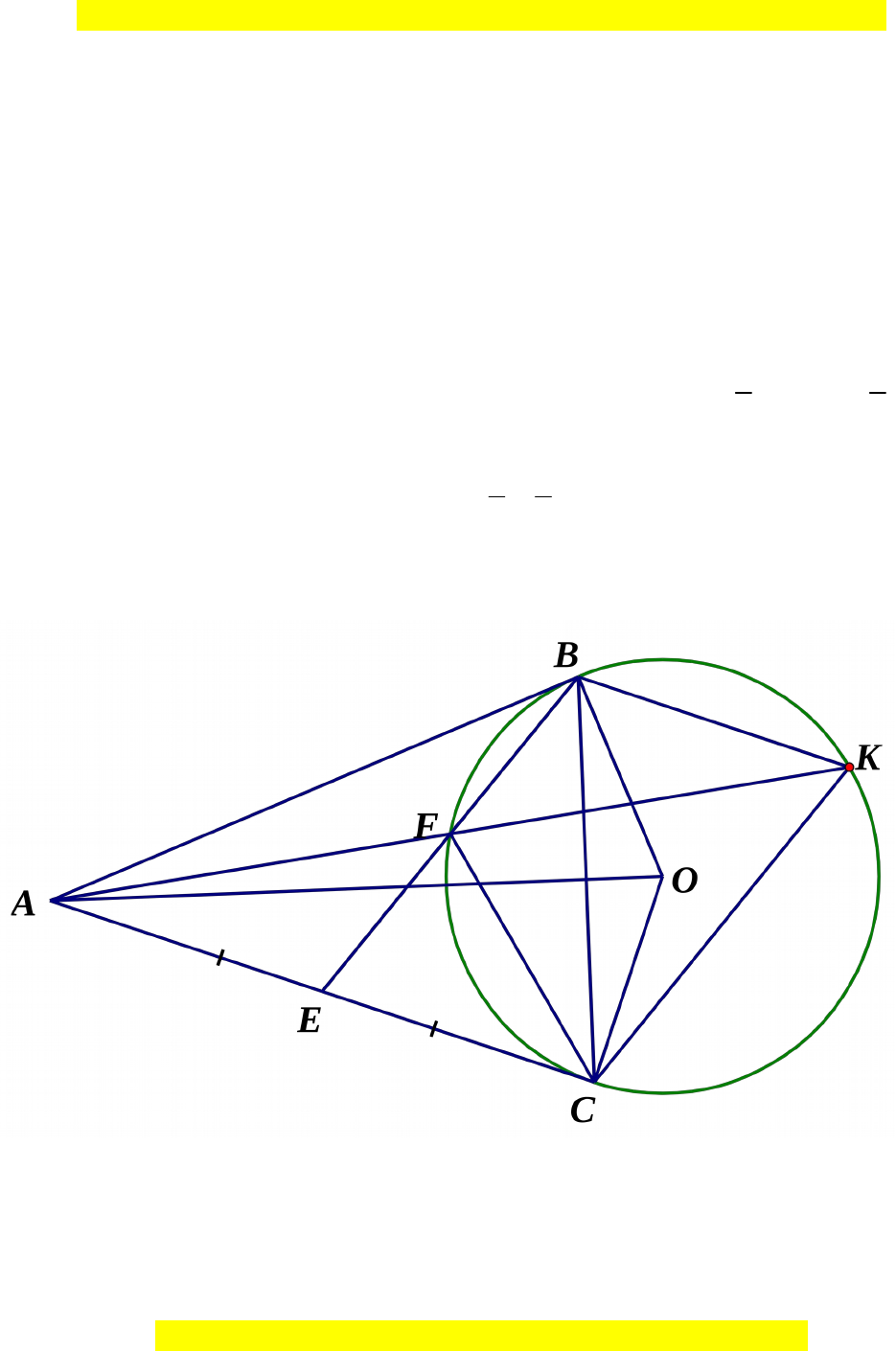
Câu 4. (3,0 đi m) ể Qua đi m ể
A
n m ngoài đ ng tròn (O) v hai ti p tuy n ằ ườ ẽ ế ế
,AB AC
c a đ ng tròn (ủ ườ
,B C
là hai ti p đi m). G i E là trung đi m c a đo n ế ể ọ ể ủ ạ
,AC F
là giao
đi m th hai c a ể ứ ủ
EB
v i đ ng tròn (O).ớ ườ
a) Ch ng minh : t giác ứ ứ
ABOC
là t giác n i ti p, tam giác ứ ộ ế
CEF
đ ng d ng v i ồ ạ ớ
tam giác
.BEC
b) G i K là giao đi m th hai c a đ ng th ng ọ ể ứ ủ ườ ẳ
AF
v i đ ng tròn (O). Ch ng ớ ườ ứ
minh
. .BF CK BK CF
c) Ch ng minh ứ
AE
là ti p tuy n c a đ ng tròn ngo i ti p tam giác ế ế ủ ườ ạ ế
ABF
Câu 5. (1,0 đi m) ể Xét các s ố
, ,x y z
thay đ i th a mãn ổ ỏ
3 3 3
3 2.x y z xyz
Tìm giá
tr nh nh t c a bi u th c: ị ỏ ấ ủ ể ứ
2
2 2 2
1
4
2
P x y z x y z xy yz zx
M iọ th c m c vui lòng xin liên hắ ắ ệ hotline: 084 283 45 85
Đây là b nả xem thử, vui lòng mua tài li u đ xem chi ti t (có l i gi i)ệ ể ế ờ ả
ĐÁP ÁN
I. Ph n tr c nghi mầ ắ ệ
1B 2A 3C 4B 5D 6C 7D 8C
II. Ph n t lu nầ ự ậ
Câu 1.
2 2
) 3 2 2 3 2 2 2 1 2 1
2 1 2 1 2 1 2 1 2
a A
b) Ta có:
2 1 6
. 3
9
3 3
3 6 3
2 2 1( )
3 3 3
a
a
a a
a a
dfcm
a a a
Câu 2.
a) V i ớ
0m
, ta có
1
tr thành ở
2
2 6 0x x
' 7 0
ph ng trình có hai nghi m ươ ệ
1 2
1 7, 1 7x x
b) Ta có
6 0ac
nên v i m i giá tr c a ớ ọ ị ủ
m
ph ng trình đã cho luôn có hai ươ
nghi m phân bi tệ ệ
c) Ta có:
1 2
2 2
2 1 2 2
1 2
2
, 2 6 0 2 6
6
x x m
x m x x m x
x x
Khi đó
2
2 1 2 1 2 1 2 1
2 16 2 6 2 16x x x m x m x x x m x
2 2
1 2 1 2
0
2 10 2 6 10 2 4
4
m
m x x x x m m
m
Câu 3. Gi i h ph ng trình ả ệ ươ
2
2
7 0 (1)
2 4 1 (2)
x xy y
x xy y x
M iọ th c m c vui lòng xin liên hắ ắ ệ hotline: 084 283 45 85
Đây là b nả xem thử, vui lòng mua tài li u đ xem chi ti t (có l i gi i)ệ ể ế ờ ả
Ta có:
2
2
2 2 2 0 2 2 0
2
x
x y x x x y
y x
V i ớ
2,x
ta có
1
tr thành ở
4 2 7 0 3y y y
V i ớ
2 ,y x
ta có:
1
tr thành ở
2 2
1 3
2 2 7 0 2 3 5 0
5 1
2 2
x y
x x x x x x
x y
V y h có nghi m ậ ệ ệ
5 1
; 2; 3 ; 1;3 ; ;
2 2
x y
Câu 4.
a) Ta có
AB
là ti p tuy n c a đ ng tròn (O) nên ế ế ủ ườ
0
90ABO
T ng t ươ ự
0
90ACO
M iọ th c m c vui lòng xin liên hắ ắ ệ hotline: 084 283 45 85
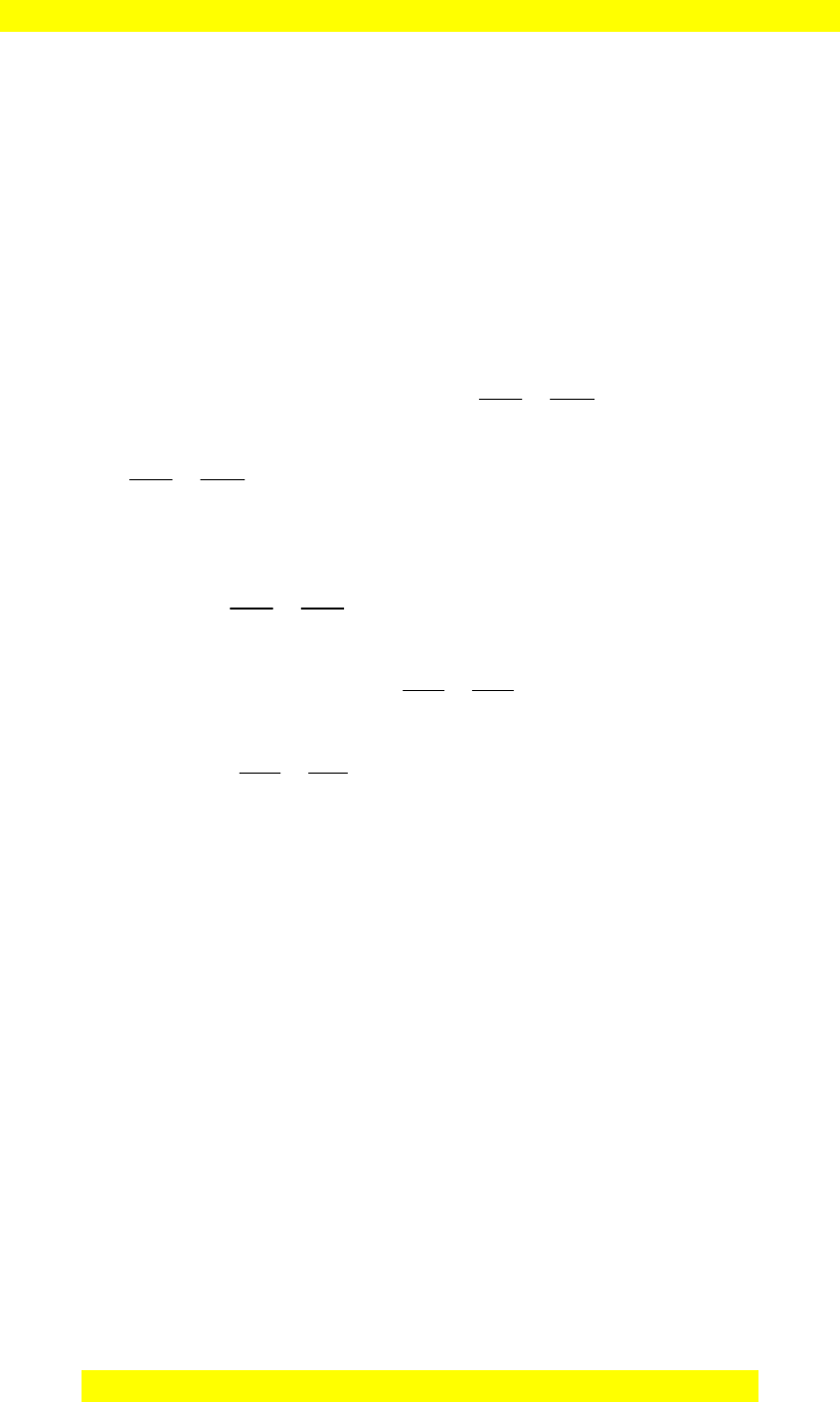
Đây là b nả xem thử, vui lòng mua tài li u đ xem chi ti t (có l i gi i)ệ ể ế ờ ả
Xét t giác ứ
ABOC
có
0
180ABO ACO
mà hai góc này vi trí đ i nhau nên t giácở ố ứ
ABOC
là t giác n i ti p.ứ ộ ế
Xét đ ng tròn (O) có ườ
ECF
là góc t o b i tia ti p tuy n và dây cung, ạ ở ế ế
CBF
là góc n i ộ
ti p cùng ch n ế ắ
CF
nên
ECF CBF
hay
ECF EBC
Xét
CEF
và
BEC
có
E
chung;
ECF EBC
( . )CEF BEC g g
b) Ch ng minh đ c ứ ượ
( . ) (1)
BF AB
ABF AKB g g
BK AK
T ng t : ươ ự
(2)
CF AC
CK AK
L i có: ạ
,AB AC
là hai ti p tuy n c a (O) nên ế ế ủ
(3)AB AC
T (1) (2) (3) suy ra ừ
. .
BF CF
BF CK BK CF
BK CK
c) T ừ
CEF
đ ng d ng v i ồ ạ ớ
EF EC
BEC
EC EB
L i có: ạ
EA EC
nên
EF EA
EA EB
Suy râ
( . . )AEF BEA c g c EAF EBA
hay
EAF ABF
Trên n a m t ph ng b AB có ch a đi m E k tia ử ặ ẳ ờ ứ ể ẻ
Ax
là tia ti p tuy n c a đ ng trònế ế ủ ườ
ngo i ti p ạ ế
ABF
Ch ng minh đ c : ứ ượ
EAF xAF
(cùng b ng ằ
)ABF
tia
AE
trùng v i tia ớ
Ax
V y ậ
AE
là ti p tuy n c a đ ng tròn ngo i ti p ế ế ủ ườ ạ ế
.ABF
Câu 5.
Ta có:
3 3 3 2 2 2
2 3x y z xyz x y z x y z xy yz zx
Suy ra
2 2 2
0x y z xy yz zx
Ch ng minh đ c: ứ ượ
2 2 2
0x y z xy yz zx
v i m i ớ ọ
, ,x y z
M iọ th c m c vui lòng xin liên hắ ắ ệ hotline: 084 283 45 85