SỞ GIÁO D C Ụ VÀ ĐÀO T O Ạ KỲ THI TUY N Ể SINH VÀO L P Ớ 10 THPT THỪA THIÊN HUẾ
Khóa ngày 18 tháng 7 năm 2020 Môn thi: TOÁN D Ề THI CHÍNH TH C Ứ Th i
ờ gian làm bài : 120 phút (không kể giao đề) Câu 1. (1,5 đi m) ể a) Không s d ử ng m ụ
áy tính cầm tay, tính giá tr bi ị u t ể h c ứ A 25 16 b) Đ a ư th a ừ s ra
ố ngoài dấu căn, tính giá tr c ị a ủ bi u t ể h c
ứ B 9.2 2 25.2 2 16.2 x 1 x 1 C : 1 x x x x x c) Rút g n bi ọ u t ể h c ứ v i ớ x 0, x 1 Câu 2. (1,5 đi m) ể x y 3 3
y 2x 5 a) Không s d ử ng m ụ áy tính cầm tay, gi i ả h ph ệ ư ng ơ trình y m x 2m m 0 b) Tìm giá trị c a ủ m đ đ ể ư ng t ờ h ng ẳ
song song v iớ đư ng t ờ hẳng y 2 x 2020 Câu 3. (1,0 đi m) ể Để xây d ng t ự hành ph H ố uế ngày càng đ p h ẹ n và ơ khuy n khí ế ch người dân rèn luy n s ệ c ứ kh e ỏ , y ba Ủ n nhân dân t nh ỉ Thừa Thiên Hu đã ế cho xây d ng t ự uy n ế đư ng đi ờ b ve ộ n b B ờ c ắ sông Hư ng, t ơ c ừ ầu Trư ng ờ
Tiền đến cầu Dã Viên có chi u dà ề i 2km. M t ộ người đi b t ộ rên tuy n ế đư ng ờ 17 này, kh i ở hành t c ừ ẩu Trư ng ờ Ti n đ ề n c ế ầu Dã Viên r i ồ quay v l ề i ạ c u ầ Trư ng ờ Ti n h ề t ế t t ấ c ả 18 gi . ờ Tính vận t c ố c a ủ ngư i ờ đó lúc v , bi ề t ế r ng v ằ n t ậ c ố lúc đi l n h ớ n v ơ n t ậ c ố lúc v l ề à 0,5km / . h Câu 4. (2,0 đi m) ể 2
x m 1 x m 0 Cho phư ng ơ trình: 1 (v iớ x là n s ẩ ố a) Giải phư ng ơ trình 1 ki m 2 b) Ch ng ứ minh phư ng ơ trình 1 luôn có nghi m ệ v i ớ mọi giá tr c ị ủa m x , x c) Tìm các giá tr c
ị ủa m để phư ng ơ trình 1 có nghi m ệ 1 2 thỏa mãn đi u ki ề n ệ 2 2
x x x x 12 0 1 2 1 2 Câu 5. (3,0 đi m) ể
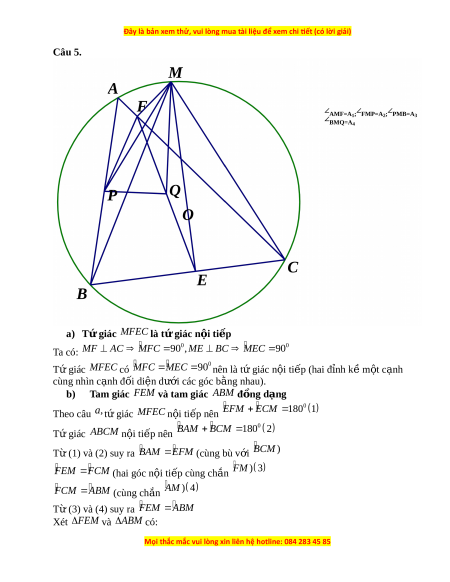
Cho tam giác ABC có ba góc nh n n ọ i ộ ti p đ ế ư ng ờ tròn tâm . O G i
ọ M là một điểm bất kỳ trên cung nh
ỏ AC sao cho BCM nh n ọ (M không trùng A và C). G i
ọ E và F lần lượt là chân các AB Q đư ng ờ vuông góc k t
ẻ ừ M đến BC và AC. G i ọ P là trung đi m ể c a ủ , là trung đi m ể c a ủ FE.Ch ng ứ minh rằng : a) Tứ giác MFEC n i ộ tiếp
b) Tam giác FEM và tam giác ABM đ ng d ồ ạng M . A MQ M . P MF 0 PQM 90 c) và
Câu 6. (1,0 đi m) ể M t ộ chiếc cốc th y
ủ tinh có dạng hình tr , c ụ hi u
ề cao bằng 10cm và ch a ứ m t ộ lư ng ợ nư c ớ có thể tích bằng m t ộ n a ử thể tích chi c ế cốc.M t ộ chi c ế c c ố th y t ủ inh khác có d ng hì ạ nh nón (không
chứa gì cả) và có bán kính đáy bằng bán kính đáy chiếc c c ố hình tr đã ụ cho. Bi t ế rằng khi đổ h t ế lư ng n ợ ư c ớ trong chiếc c c ố hình trụ vào chi c ế c c ố hình nón thì chi c
ế cốc hình nón đầy nư c ớ và không có nư c
ớ tràn ra ngoài. Tính chi c ế cao của chi c ế c c ố d ng hì ạ nh nón (b qua ỏ b dà ề y thành c c ố và đáy c c ố ). ĐÁP ÁN Câu 1.
a)A 25 16 5 4 1
b)B 9.2 2 25.2 2 16.2 3 2 2.5 2 2.4 2 3 2 10 2 8 2 2 x 1 x 1 x 1 x x 1 c)C : 1 : x x x x x x x 1
x. x 1 x 1 1 x x 1 x x 1 x . . . x x 1 x 1
x. x 1 x 1
x. x 1 x 1 1 x 1 Câu 2. x y 3 2x 2 y 6 y 1 x 4 a) 3y 2x 5 2x 3y 5 x y 3 y 1 V y ậ h ph ệ ư ng t ơ rình có nghi m ệ duy nh t ấ ; x y 4; 1 b) Tìm giá tr c ị a m ủ Để đư ng t ờ h ng ẳ y mx 2m m 0 song song v i ớ đư ng ờ th ng ẳ y 2 x 2020 thì m 2 m 2 m 2( tm) 2m 2020 m 1010 V y ậ m 2 Câu 3. G i ọ v n t ậ ốc lúc v c ề a ủ ngư i
ờ đó là x km / h x 0 Suy ra v n t
ậ ốc lúc đi : x 0,5(km / h) 2 h 2 (h) Th i
ờ gian lúc đi: x 0,5 Th i ờ gian lúc v : ề x
Vì ngư i ờ đó kh i ở hành t c ừ u ầ Trư ng ờ Ti n đ ề n c ế u D ầ ã Viên r i ồ quay v l ề i ạ c u ầ 17 Trư ng ờ Ti n h ề t ế tất c ả 18 gi nên ờ ta có phư ng t ơ rình: 2 2 17
36x 36 x 0,5 17
x x 0,5 x 0,5 x 18 17 127 2 2
36x 36x 18 17 x x 17x x 18 0 2 2 2 2
34x 127x 36 0
34x 136x 9x 36 0
34x x 4 9 x 4 0
x 4 34x 9 0 x 4( tm) x 4 0 9 34x 9 0 x (ktm) 34 V y ậ v n t ậ ốc ngư i ờ đó lúc v l ề à 4km / h Câu 4. a) Giải phư ng t ơ rình(1) khi m 2 V i ớ m 2 thì phư ng t ơ rình (1) tr t ở hành: 2 2 x 3x 2 0
x x 2x 2 0
x x 1 2 x 1 0 x 1 0 x 1 x 1 x 2 0 x 2 0 x 2 V y ậ v i ớ m 2 thì phư ng ơ trình (1) có hai nghi m ệ x 1 ; x 2 b) Chứng minh phư ng
ơ trình (1) luôn có hai nghi m ệ v i ớ m i ọ m 2 Xét phư ng
ơ trình x m 1 x m 0 1 2 2 2 2
m 1 4.1.m m
2m 1 4m m
2m 1 m 1 Ta có: Vì m 2 1 0 nên 0 m Suy ra phư ng t ơ rình (1) luôn có hai nghi m ệ v i ớ m i ọ giá tr m ị c) Tìm các giá tr m ị …. Theo câu b phư ng ơ trình luôn có hai nghi m ệ v i ớ m i ọ m x x m 1 1 2 Khi đó, áp d ng ụ h t ệ h c
ứ Vi – et ta có: x x m 1 2 Theo bài ra ta có:
2 2
x x x x 12 0
x x x x 12 0 1 2 1 2 1 2 1 2
m m 2 1 12 0
m m 12 0 m 4
m 4 m 3 0 m 3 V y
ậ m 4;m 3 th a m ỏ ãn yêu cầu đ bài ề .
Đề thi vào 10 môn Toán tỉnh Thừa Thiên Huế (Hệ không chuyên) năm 2021
492
246 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ 69 đề thi vào 10 môn Toán hệ không chuyên mới nhất năm 2021 nhằm giúp Giáo viên có thêm tài liệu tham khảo đề luyện thi Toán ôn luyện vào 1
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(492 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Ôn vào 10
Xem thêmTài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi ết (có lời giải)
S GIÁO D C VÀ ĐÀO T O Ở Ụ Ạ
TH A THIÊN HUỪ Ế
D THI CHÍNH TH C Ề Ứ
KỲ THI TUY N SINH VÀO L P 10 THPTỂ Ớ
Khóa ngày 18 tháng 7 năm 2020
Môn thi: TOÁN
Th i gian làm bài : 120 phút ờ (không k giao đ )ể ề
Câu 1. (1,5 đi m)ể
a) Không s d ng máy tính c m tay, tính giá tr bi u th c ử ụ ầ ị ể ứ
25 16A
b) Đ a th a s ra ngoài d u căn, tính giá tr c a bi u th c ư ừ ố ấ ị ủ ể ứ
9.2 2 25.2 2 16.2B
c) Rút g n bi u th c ọ ể ứ
1 1
: 1
x x
C
x x x x x
v i ớ
0, 1x x
Câu 2. (1,5 đi m) ể
a) Không s d ng máy tính c m tay, gi i h ph ng trình ử ụ ầ ả ệ ươ
3
3 2 5
x y
y x
b) Tìm giá tr c a m đ đ ng th ng ị ủ ể ườ ẳ
2 0y mx m m
song song v i đ ng th ngớ ườ ẳ
2 2020y x
Câu 3. (1,0 đi m)ể
Đ xây d ng thành ph Hu ngày càng đ p h n và khuy n khích ng i dân rèn luy n s c ể ự ố ế ẹ ơ ế ườ ệ ứ
kh e, y ban nhân dân t nh Th a Thiên Hu đã cho xây d ng tuy n đ ng đi b ven b B c sông ỏ Ủ ỉ ừ ế ự ế ườ ộ ờ ắ
H ng, t c u Tr ng Ti n đ n c u Dã Viên có chi u dài 2km. M t ng i đi b trên tuy n đ ng ươ ừ ầ ườ ề ế ầ ề ộ ườ ộ ế ườ
này, kh i hành t c u Tr ng Ti n đ n c u Dã Viên r i quay v l i c u Tr ng Ti n h t t t c ở ừ ẩ ườ ề ế ầ ồ ề ạ ầ ườ ề ế ấ ả
17
18
gi . Tính v n t c c a ng i đó lúc v , bi t r ng v n t c lúc đi l n h n v n t c lúc v là ờ ậ ố ủ ườ ề ế ằ ậ ố ớ ơ ậ ố ề
0,5 / .km h
Câu 4. (2,0 đi m)ể
Cho ph ng trình:ươ
2
1 0x m x m
1
(v i ớ
x
là n sẩ ố
a) Gi i ph ng trình ả ươ
1
ki
2m
b) Ch ng minh ph ng trình ứ ươ
1
luôn có nghi m v i m i giá tr c a ệ ớ ọ ị ủ
m
c) Tìm các giá tr c a ị ủ
m
đ ph ng trình ể ươ
1
có nghi mệ
1 2
,x x
th a mãn đi u ki nỏ ề ệ
2 2
1 2 1 2
12 0x x x x
Câu 5. (3,0 đi m) ể
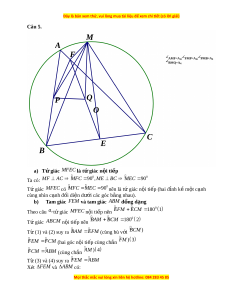
Cho tam giác
ABC
có ba góc nh n n i ti p đ ng tròn tâm ọ ộ ế ườ
.O
G i ọ
M
là m t đi m b t kỳ ộ ể ấ
trên cung nh ỏ
AC
sao cho
BCM
nh n ọ
(M
không trùng A và C). G i ọ
E
và F l n l t là chân các ầ ượ
đ ng vuông góc k t ườ ẻ ừ
M
đ n ế
BC
và
.AC
G i ọ
P
là trung đi m c a ể ủ
,AB Q
là trung đi m c aể ủ
.FE
Ch ng minh r ng :ứ ằ
a) T giác ứ
MFEC
n i ti pộ ế
b) Tam giác
FEM
và tam giác
ABM
đ ng d ngồ ạ
c)
. .MA MQ MP MF
và
0
90PQM
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi ết (có lời giải)
Câu 6. (1,0 đi m)ể
M t chi c c c th y tinh có d ng hình tr , chi u cao b ng ộ ế ố ủ ạ ụ ề ằ
10cm
và ch a m t l ng n c có ứ ộ ượ ướ
th tích b ng m t n a th tích chi c c c.M t chi c c c th y tinh khác có d ng hình nón (không ể ằ ộ ử ể ế ố ộ ế ố ủ ạ
ch a gì c ) và có bán kính đáy b ng bán kính đáy chi c c c hình tr đã cho. Bi t r ng khi đ h t ứ ả ằ ế ố ụ ế ằ ổ ế
l ng n c trong chi c c c hình tr vào chi c c c hình nón thì chi c c c hình nón đ y n c và ượ ướ ế ố ụ ế ố ế ố ầ ướ
không có n c tràn ra ngoài. Tính chi c cao c a chi c c c d ng hình nón (b qua b dày thành c c ướ ế ủ ế ố ạ ỏ ề ố
và đáy c c).ố
ĐÁP ÁN
Câu 1.
) 25 16 5 4 1
) 9.2 2 25.2 2 16.2 3 2 2.5 2 2.4 2
3 2 10 2 8 2 2
1 1 1 1
) : 1 :
1 . 1
1 1 1 1
. . .
1 1 1 1
. 1 . 1
1
1
a A
b B
x x x x x
c C
x x x x x x
x x x x
x x x x x
x x x x x
x x x x
x
Câu 2.
3 2 2 6 1 4
)
3 2 5 2 3 5 3 1
x y x y y x
a
y x x y x y y
V y h ph ng trình có nghi m duy nh t ậ ệ ươ ệ ấ
; 4;1x y
b) Tìm giá tr c a mị ủ
Đ đ ng th ng ể ườ ẳ
2 0y mx m m
song song v i đ ng th ng ớ ườ ẳ
2 2020y x
thì
2 2
2( )
2 2020 1010
m m
m tm
m m
V y ậ
2m
Câu 3.
G i v n t c lúc v c a ng i đó là ọ ậ ố ề ủ ườ
/ 0x km h x
Suy ra v n t c lúc đi : ậ ố
0,5( / )x km h
Th i gian lúc đi: ờ
2
0,5
h
x
Th i gian lúc v : ờ ề
2
( )h
x
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi ết (có lời giải)
Vì ng i đó kh i hành t c u Tr ng Ti n đ n c u Dã Viên r i quay v l i c u ườ ở ừ ầ ườ ề ế ầ ồ ề ạ ầ
Tr ng Ti n h t t t c ườ ề ế ấ ả
17
18
gi nên ta có ph ng trình:ờ ươ
2 2
2 2
2 2 17
36 36 0,5 17 0,5
0,5 18
17 127
36 36 18 17 17 18 0
2 2
34 127 36 0 34 136 9 36 0
34 4 9 4 0 4 34 9 0
4( )
4 0
9
34 9 0
( )
34
x x x x
x x
x x x x x x
x x x x x
x x x x x
x tm
x
x
x ktm
V y v n t c ng i đó lúc v là ậ ậ ố ườ ề
4 /km h
Câu 4.
a) Gi i ph ng trình(1) khi ả ươ
2m
V i ớ
2m
thì ph ng trình (1) tr thành:ươ ở
2 2
3 2 0 2 2 0 1 2 1 0
1 0 1
1 2 0
2 0 2
x x x x x x x x
x x
x x
x x
V y v i ậ ớ
2m
thì ph ng trình (1) có hai nghi m ươ ệ
1; 2x x
b) Ch ng minh ph ng trình (1) luôn có hai nghi m v i m i mứ ươ ệ ớ ọ
Xét ph ng trình ươ
2
1 0 1x m x m
Ta có:
2
2
2 2
1 4.1. 2 1 4 2 1 1m m m m m m m m
Vì
2
1 0m
nên
0 m
Suy ra ph ng trình (1) luôn có hai nghi m v i m i giá tr mươ ệ ớ ọ ị
c) Tìm các giá tr m….ị
Theo câu b ph ng trình luôn có hai nghi m v i m i mươ ệ ớ ọ
Khi đó, áp d ng h th c Vi – et ta có: ụ ệ ứ
1 2
1 2
1x x m
x x m
Theo bài ra ta có:
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi ết (có lời giải)
2 2
1 2 1 2 1 2 1 2
2
12 0 12 0
1 12 0 12 0
4
4 3 0
3
x x x x x x x x
m m m m
m
m m
m
V y ậ
4; 3m m
th a mãn yêu c u đ bài.ỏ ầ ề
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi ết (có lời giải)
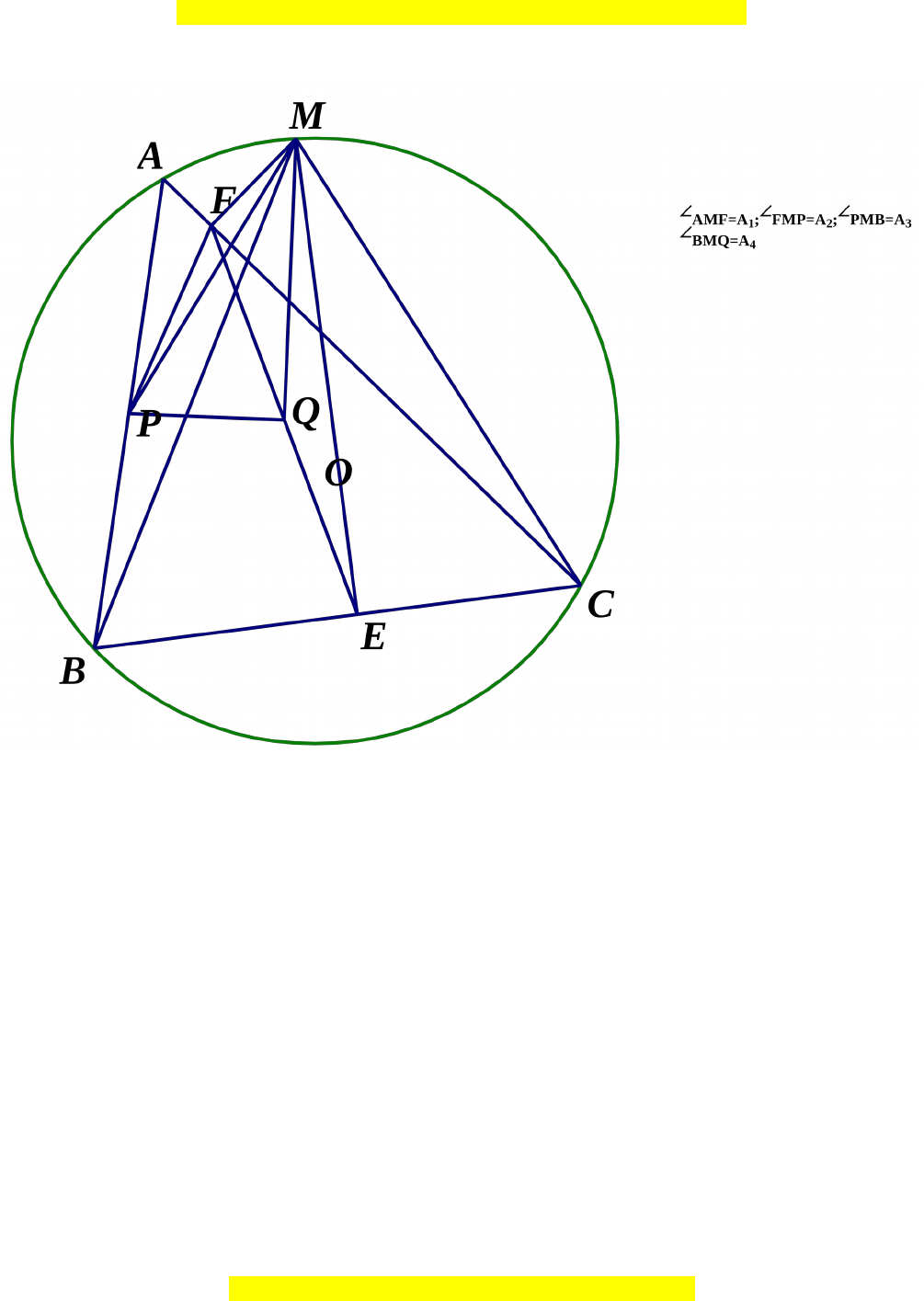
Câu 5.
a) T giác ứ
MFEC
là t giác n i ti pứ ộ ế
Ta có:
0 0
90 , 90MF AC MFC ME BC MEC
T giác ứ
MFEC
có
0
90MFC MEC
nên là t giác n i ti p (hai đ nh k m t c nh ứ ộ ế ỉ ề ộ ạ
cùng nhìn c nh đ i di n d i các góc b ng nhau).ạ ố ệ ướ ằ
b) Tam giác
FEM
và tam giác
ABM
đ ng d ngồ ạ
Theo câu
,a
t giác ứ
MFEC
n i ti p nên ộ ế
0
180 1EFM ECM
T giác ứ
ABCM
n i ti p nên ộ ế
0
180 2BAM BCM
T (1) và (2) suy ra ừ
BAM EFM
(cùng bù v i ớ
)BCM
FEM FCM
(hai góc n i ti p cùng ch n ộ ế ắ
) 3FM
FCM ABM
(cùng ch n ắ
) 4AM
T (3) và (4) suy ra ừ
FEM ABM
Xét
FEM
và
ABM
có:
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85