Giáo án Powerpoint Biến cố và định nghĩa cổ điển của xác suất Toán 10 Kết nối tri thức

CHƯƠNG IX. CH TÍNH XÁC S ƯƠN UẤT G I
THEO ĐỊNH NGHĨA CỔ ĐIỂN TOÁN ĐẠI 26
BIẾN CỐ VÀ ĐỊNH NGHĨA CỔ ĐIỂN SỐ ➉ CỦA XÁC SUẤT
3 NGUYÊN LÝ XÁC SUẤT BÉ BÀI TẬP 4 Ví dụ 5.
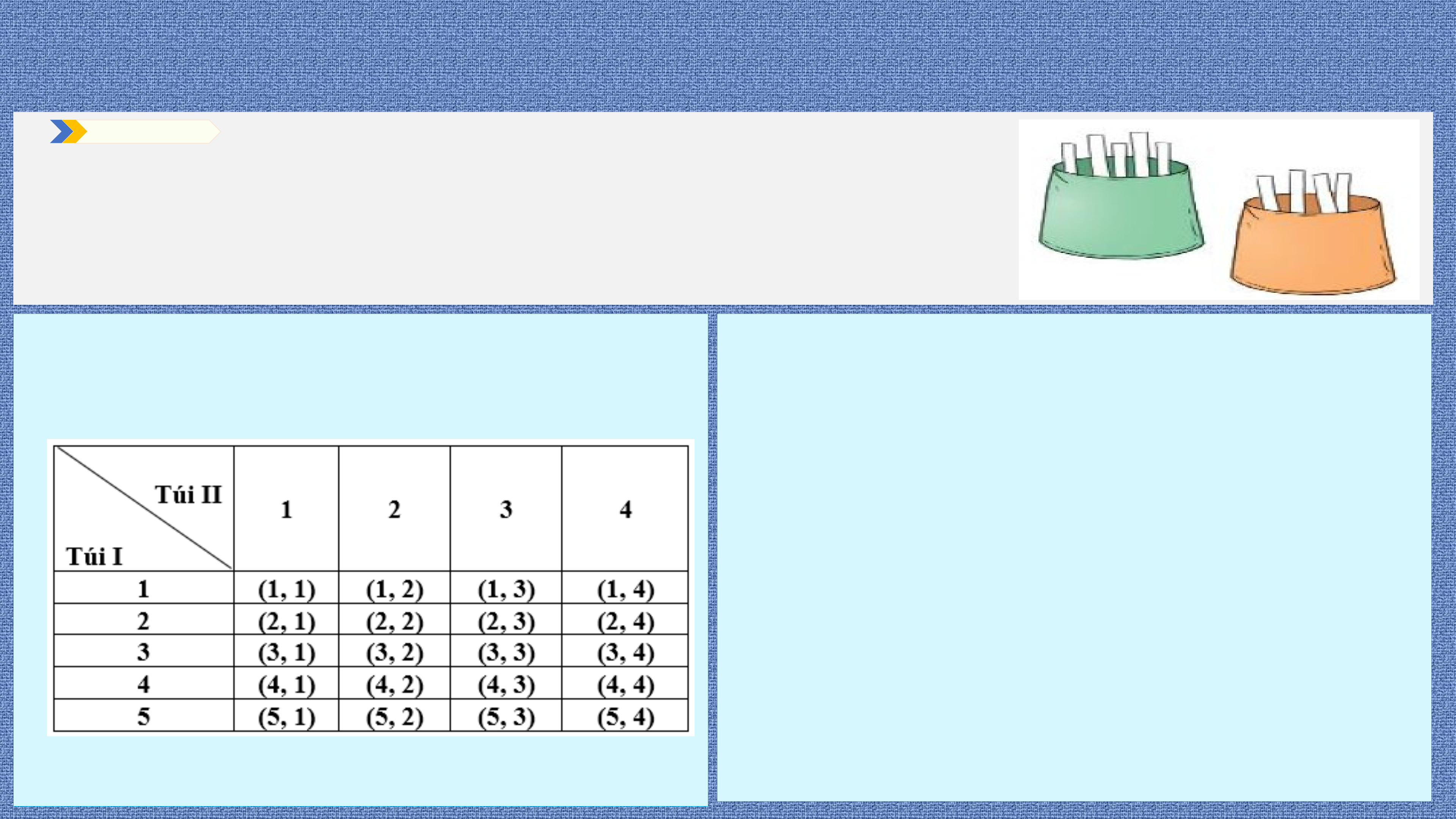
Hai túi I và II chứa các tấm thẻ được đánh số.
Túi I : {1; 2; 3; 4; 5}, túi I
I: {1; 2; 3; 4}. Rút ngẫu nhiên một tấm
thẻ từ mỗi túi I và II. Tính xác suất để tổng
hai số trên hai tấm thẻ lớn hơn 6. Lời giải vậy .
• Mô tả không gian mẫu bằng cách • Biến cố E: “Tổng hai số trên hai tấm lập bảng như sau.
thẻ lớn hơn 6” xảy ra khi tổng là một trong ba trường hợp:
Tổng bằng 7 gồm các kết quả: (3, 4): (4, 3); (5, 2).
Tổng bằng 8 gồm các kết quả: (4, 4): (5, 3).
Tổng bằng 9 có một kết quả: (5, 4).
Vậy biến cố E= {(3,4): (4,3); (5,2); (4,4):
(5,3): (5,4)}. Từ đó n(E) = 6 và
Mỗi ô là một kết quả có thể. Có 20 ô, .
Chú ý. Trong những phép thử đơn giản, ta đếm số phần tử
của tập và số phần tử của biến cố E bằng cách liệt kê ra tất
cả các phần tử của hai tập hợp này.
Luyện tập 3 3. Gieo đồng thời hai
• Xác suất để tồng số chấm
con súc sắc cân đối. Tính xác suất
xuất hiện trên hai con súc sắc
để tồng số chấm xuất hiện trên hai
bằng 4 hoặc bằng 6:
con súc sắc bằng 4 hoặc bằng 6. • . Lời giải
• Số phần tử của không gian mẫu: n(Ω)=6.6=36.
• Gọi biến cố A: “Tổng số chấm
xuất hiện trên hai con súc sắc
bằng 4 hoặc bằng 6” ta có:
A={(i;j)|i,j∈N;1≤i≤5;1≤j≤5}
• A={(1,3);(3,1);(2,2);(1,5);(5,1); (2,4);(4,2);(3,3)} ⇒n(A)=8.
3. NGUYÊN LÍ XÁC SUẤT BÉ
Nếu một biến cố có xác suất rất bé thì trong một phép thử
biến cố đó sẽ không xảy ra.
• Chẳng hạn, xác suất một chiếc • Chú ý. Trong thực tế, xác suất
máy bay rơi là rất bé, khoảng
của một biến cố được coi là bé
0,00000027. Mỗi hành khách
phụ thuộc vào từng trường hợp
khi đi máy bay đều tin rằng
cụ thề. Chẳng hạn, xác suất một
biến cố: “Máy bay rơi” sẽ
chiếc điện thoại bị lỗi kĩ thuật là
không xảy ra trong chuyến
0,001 được coi là rất bé, nhưng
bay của mình, do đó người ta
nếu xác suất cháy nồ động cơ
vẫn không ngần ngại đi máy
của một máy bay là 0,001 thì xác bay.
suất này không được coi là rất bé.