Trường:……………………………..
Họ và tên giáo viên: …………………………… Tổ: TOÁN
Ngày dạy đầu tiên:……………………………..
Ngày soạn: …../…../2021 Tiết:
BÀI 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN
Môn học/Hoạt động giáo dục: Toán - HH: 12
Thời gian thực hiện: ..... tiết I. MỤC TIÊU 1. Kiến thức
- Biết khái niệm về thể tích khối đa diện.
- Biết công thức tính thể tích các khối lăng trụ và khối chóp.
- Tính được thể tích khối lăng trụ và khối chóp.
- Vận dụng việc tính thể tích để giải quyết một số bài toán thực tế. 2. Năng lực
- Năng lực hợp tác: Tổ chức nhóm học sinh hợp tác thực hiện các hoạt động.
- Năng lực tự học, tự nghiên cứu: Học sinh tự giác tìm tòi, lĩnh hội kiến thức và phương pháp giải
quyết bài tập và các tình huống.
- Năng lực giải quyết vấn đề: Học sinh biết cách huy động các kiến thức đã học để giải quyết các
câu hỏi. Biết cách giải quyết các tình huống trong giờ học.
- Năng lực sử dụng công nghệ thông tin: Học sinh sử dụng máy tính, mang internet, các phần mềm
hỗ trợ học tập để xử lý các yêu cầu bài học.
3. Phẩm chất:
- Rèn luyện tư duy logic, thái độ chủ động, tích cực trong học tập.
- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần hợp tác xây dựng cao.
- Say sưa, hứng thú trong học tập và tìm tòi nghiên cứu liên hệ thực tiễn.
- Tư duy vấn đề có lôgic và hệ thống.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU - Máy chiếu - Bảng phụ - Phiếu học tập
III. TIẾN TRÌNH DẠY HỌC :
1. HOẠT ĐỘNG 1: MỞ ĐẦU
a) Mục tiêu: Tạo tâm thế học tập cho học sinh, giúp các em ý thức được nhiệm vụ học tập, sự cần
thiết phải tìm hiểu về các vấn đề đã nêu ra từ đó gây được hứng thú với việc học bài mới.
b) Nội dung: Hãy quan sát các hình sau và trả lời các câu hỏi.
Câu 1: Khối Rubik (H1) có các ô vuông tô màu kích thước 1cm. Hỏi thể tích của khối Rubik bằng bao nhiêu?
Câu 2: Cần bao nhiêu khối đất, đá để đắp được khối kim tự tháp là hình chóp tứ giác đều có độ dài
cạnh đáy là 230m , chiều cao là 147m ( H2).
Câu 3: Có thể xếp hết hay không các vali ở hình 3 vào khoang hành lý ôtô ở hình 4?
Hình 1 Hình 2 Hình 3 Hình 4
Như vậy, thể tích của một khối đa diện được tính như thế nào? c) Sản phẩm: Câu trả lời của HS
Học sinh quan sát hình vẽ, đọc các câu hỏi nhưng chưa trả lời được các câu hỏi.
d) Tổ chức thực hiện:
*) Chuyển giao nhiệm vụ : GV chiếu các hình vẽ và nêu câu hỏi
*) Thực hiện: HS suy nghĩ độc lập
*) Đánh giá, nhận xét, tổng hợp:
- Từ phần trả lời của HS, GV dẫn dắt vào bài mới.
2.HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚI
I. NỘI DUNG 1: KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN (SGK)
a) Mục tiêu: Hình thành khái niệm về thể tích khối đa diện, nhắc lại công thức tính thể tích khối
lập phương, khối hộp chữ nhật b)Nội dung:
Câu hỏi 1. Nêu khái niệm thể tích khối đa diện
Câu hỏi 2: Mỗi khối đa diện (H) có một thể tích là là một số âm hay dương, số đó có duy nhất?
Câu hỏi 3: Hai khối đa diện bằng nhau thể tích có bằng nhau không?
Câu hỏi 4: Nêu công thức tính thể tích khối lập phương?
Câu hỏi 5: Nêu công thức tính thể tích khối hộp chữ nhật?
Ví dụ 1: Cho khối lập phương có cạnh bằng (có thể tích
). Các khối đa diện được ghép từ
các khối lập phương có cạnh bằng (hình vẽ).
i) So sánh thể tích hai khối lập phương (hình vẽ).
So sánh thể tích hai khối lăng trụ đối xứng nhau qua một mặt phẳng (hình vẽ).
ii) Tính thể tích của khối đa diện (hình vẽ). c) Sản phẩm: Nội dung bài học
1.Khái niệm về thể tích khối đa diện.
Thể tích của một khối đa diện hiểu theo nghĩa thông thường là số đo độ lớn phần không gian mà
nó chiếm chỗ (Bao gồm phần không gian bên trong và hình đa diện). Định nghĩa:
Mỗi khối đa diện (H) có một thể tích là một số duy nhất V(H) thoả mãn các tính chất sau:
i) V(H) là một số dương;
ii) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) =1.
iii) Nếu hai khối đa diện (H) và (H’) bằng nhau thì V(H) = V(H’)
iv) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:
V(H)=V(H1 )+ V(H2). Chú ý:
Số dương V(H) nói trên cũng được gọi là thế tích của hình đa diện giới hạn khối da diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
Thể tích của khối hộp chữ nhật bằng tích ba kích thước. Ví dụ 1:
i) Hai khối lập phương có cạnh bằng 3 (bằng nhau) nên thể tích bằng nhau.
Hai khối lăng trụ bằng nhau thì có thể tích bằng nhau
ii) Khối đa diện đã cho được chia thành hai khối hình hộp chữ nhật có kích thước lần lượt:
Khối 1: 3x3x1. Khối 1 có thể tích:
Khối 2: 3x3x2, có thể tích:
d) Tổ chức thực hiện
GV: Yêu cầu học sinh đọc sách và trả lời các câu hỏi từ 1 đến 5 Chuyển giao
Hoạt động nhóm ví dụ 1 HS: Nhận
GV: điều hành, quan sát, hướng dẫn Thực hiện
HS: Cá nhân học sinh đọc sách và sau đó trao đổi cặp đôi các câu hỏi
Sau khi tiếp thu kiến thức mới học sinh hoạt động nhóm làm ví dụ
Báo cáo thảo luận HS báo cáo, theo dõi, phản biện, nhận xét
Đánh giá, nhận xét, GV nx, giải thích, làm rõ vấn đề, chốt kiến thức tổng hợp
Dẫn dắt HS chuẩn bị cho nhiệm vụ tiếp theo
II. NỘI DUNG 2: Thể tích khối lăng trụ
a) Mục tiêu: Hình thành khái niệm về thể tích khối lăng trụ . b)Nội dung:
Câu hỏi 1: Đọc sách giáo khoa trang 23 và thừa nhận định lý và nêu công thức tính thể tích khối lăng trụ?
Câu hỏi 2: Muốn tính thể tích khối lăng trụ ta cần biết những yếu tố nào?
Ví dụ 2: Cho hình lăng trụ có diện tích đáy là và chiều cao thì thể tích bằng bao nhiêu?
Ví dụ 3: Cho hình lăng trụ đứng tam giác có đáy là tam giác vuông tại ,
. Tính thể tích của khối lăng trụ. c) Sản phẩm: Nội dung bài học
2. Thể tích khối lăng trụ
Nếu xem khối hộp chữ nhật
là khối lăng trụ có đáy là hình chữ nhật và chiều cao
thì từ chú ý trên suy ra thể tích của nó bằng diện tích đáy nhân với chiều cao.
Ta có thể chứng minh được điều đó cũng đúng với khối lăng trụ bất kỳ.
Giáo án Toán 12 học kì I Hình Bài 3: Khái niệm về thể tích khối đa diện
415
208 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Bộ giáo án Toán 12 học kì I Hình được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Bộ giáo án Toán 12 học kì I Hình năm 2023 mới, chuẩn nhất được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng bài học và bám sát chương trình Sách giáo khoa Toán 12 học kì I Hình.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(415 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêm-
Bộ 10 đề thi Cuối kì 1 Toán 12 Chân trời sáng tạo có đáp án150.000 ₫ 1.1 K 563 lượt tải
-
Bộ 10 đề thi Cuối kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 1 K 491 lượt tải
-
Bộ 10 đề thi Cuối kì 1 Toán 12 Cánh diều có đáp án150.000 ₫ 503 252 lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Kết nối tri thức có đáp án150.000 ₫ 9.7 K 4.8 K lượt tải
-
Bộ 15 đề thi HSG Toán 12 có lời giải200.000 ₫ 6.9 K 3.5 K lượt tải
-
Bài giảng Powerpoint Toán 12 Kết nối tri thức350.000 ₫ 2.4 K 1.2 K lượt tải
-
Bài giảng Powerpoint Toán 12 Chân trời sáng tạo350.000 ₫ 1.2 K 622 lượt tải
-
Bộ 10 đề thi giữa kì 1 Toán 12 Chân trời sáng tạo có đáp án150.000 ₫ 2.8 K 1.4 K lượt tải
TÀI LIỆU BỘ BÁN CHẠY Lớp 12
Xem thêm-
Bộ 3 đề thi giữa kì 1 Tin học 12 Kết nối tri thức có đáp án70.000 ₫ 5 K 2.5 K lượt tải
-
Trắc nghiệm Lịch sử 12 Đúng-Sai, Trả lời ngắn (form 2025300.000 ₫ 8.2 K 4.1 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Sinh học 12 Kết nối tri thức có đáp án70.000 ₫ 4.3 K 2.2 K lượt tải
-
Bộ 5 đề thi Cuối kì 1 Tiếng Anh 12 Friends global có đáp án90.000 ₫ 426 213 lượt tải
-
Bộ 3 đề thi giữa kì 1 Sinh học 12 Chân trời sáng tạo có đáp án70.000 ₫ 1.9 K 1 K lượt tải
-
Bộ 10 đề thi giữa kì 1 Ngữ văn 12 Kết nối tri thức có đáp án150.000 ₫ 5.7 K 2.8 K lượt tải
-
Bộ 3 đề thi giữa kì 1 Vật lí 12 Chân trời sáng tạo có đáp án70.000 ₫ 1.7 K 830 lượt tải
-
Bộ 6 đề thi giữa kì 1 Lịch sử 12 Cánh diều có đáp án100.000 ₫ 5.6 K 2.8 K lượt tải
Tài liệu bộ mới nhất
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Trường:……………………………..
Tổ: TOÁN
Ngày soạn: …../…../2021
Tiết:
BÀI 3: KHÁI NIỆM VỀ THỂ TÍCH CỦA KHỐI ĐA DIỆN
!
Thời gian thực hiện: ..... tiết
I. MỤC TIÊU
1. Kiến thức
"#$%&'()$*+%
"#,)()$*-./$*01
)23()$*-./$*01
45%)()(67#&8*9:#
2. Năng lực
.-:31;,0&831:%
.-::<:,8:=&><-?$#,12@116
7#951=*
.-:67#A'89#$#,B(67#
CD"#67#=*/E
.-:8F%88F&)<&+G/G<1&'&
H/351(IF-J9
3. Phẩm chất:
KL-%2-<M<):/51
NM1%<#&-?/,&O<9#7-'7G<031IC:
+
P+82+<,Q/51=&>,-%:R
2A'0-%*
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
#
"61
S#51
III. TIẾN TRÌNH DẠY HỌC :
1. HOẠT ĐỘNG 1: MỞ ĐẦU
a) Mục tiêuCȆ<Q1G&J,23%&51<8:
#16=&('A'B/+T0C23,QO%9&O
b) Nội dung:B7+8=8+/6-ECD
Câu 1U*K9$V W0&$)2O &D()M+$*K9$9X
9+Y
Câu 2N9+$*A<(Z123$*$&:1-=01,'0
-![\&<'+- ]^&V!W
Câu 3N0(I#1#+$+-_=[$+-J_=]Y
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
= =!
=[ =]
25<()M+&$*+%23)2#Y
c) Sản phẩm:
NC/6-EM+P
87+8=`<CD22+/6-E23CD
d) Tổ chức thực hiện:
*) Chuyển giao nhiệm vụ&: a4#=`CD
*) Thực hiện:P8?-51
*) Đánh giá, nhận xét, tổng hợp:
T1/6-EM+P<a4bZ9&O
2.HOẠT ĐỘNG 2: HÌNH THÀNH KIẾN THỨC MỚI
I. NỘI DUNG 1: KHÁI NIỆM VỀ THỂ TÍCH KHỐI ĐA DIỆN (SGK)
a) Mục tiêu: =$%&'()$*+%<Z-,)()$*
-5112@<$*1c5
b)Nội dung:
NCD $%&()$*+%
NCD!H$*+%(H) 0&()- -&8*C&+2@<8*00AY
NCD[+$*+%9X+()09X+$Y
NCD],)()$*-5112@Y
NCDd,)()$*1c5Y
Ví dụ 1: N$*-5112@09X V0() WN$*+%23e1T
$*-5112@09X V=`W
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
i)P8()+$*-5112@V=`W
P8()+$*-./*I,+7+&&f1gV=`W
ii))() M+$*+%V=`W
c) Sản phẩm:
Nội dung bài học
1.Khái niệm về thể tích khối đa diện.
()M+&$*+%(G?+2E-8*-O1$+&
0#&HVBao gồm phần không gian bên trong và hình đa diệnW
Định nghĩa:
H$*+%(H) 0&()- &8*AV
(H)
6&B)A8+
iWV
(H)
-&8*2@h
iiW#(H)-$*-5112@09X =V
(H)
=1
iiiW#+$*+%(H)(H’)9X+=V
(H)
= V
(H’)
ivW#$*+%(H)231C++$*+%(H
1
)(H
2
) =
V(H)=V(H
1
)+ V(H
2
).
Chú ý
P*2@V
(H)
0/i23-#)M+=+%O$*+%
(H).
U*-5112@09X 23-khối lập phương đơn vị.
Thể tích của khối hộp chữ nhật bằng tích ba kích thước
Ví dụ 1:
W+$*-5112@09X[V9X+W()9X+
+$*-./9X+=0()9X+
WU*+%B23++$*=1c50$)2O--23
U* [I[I U* 0()
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
U*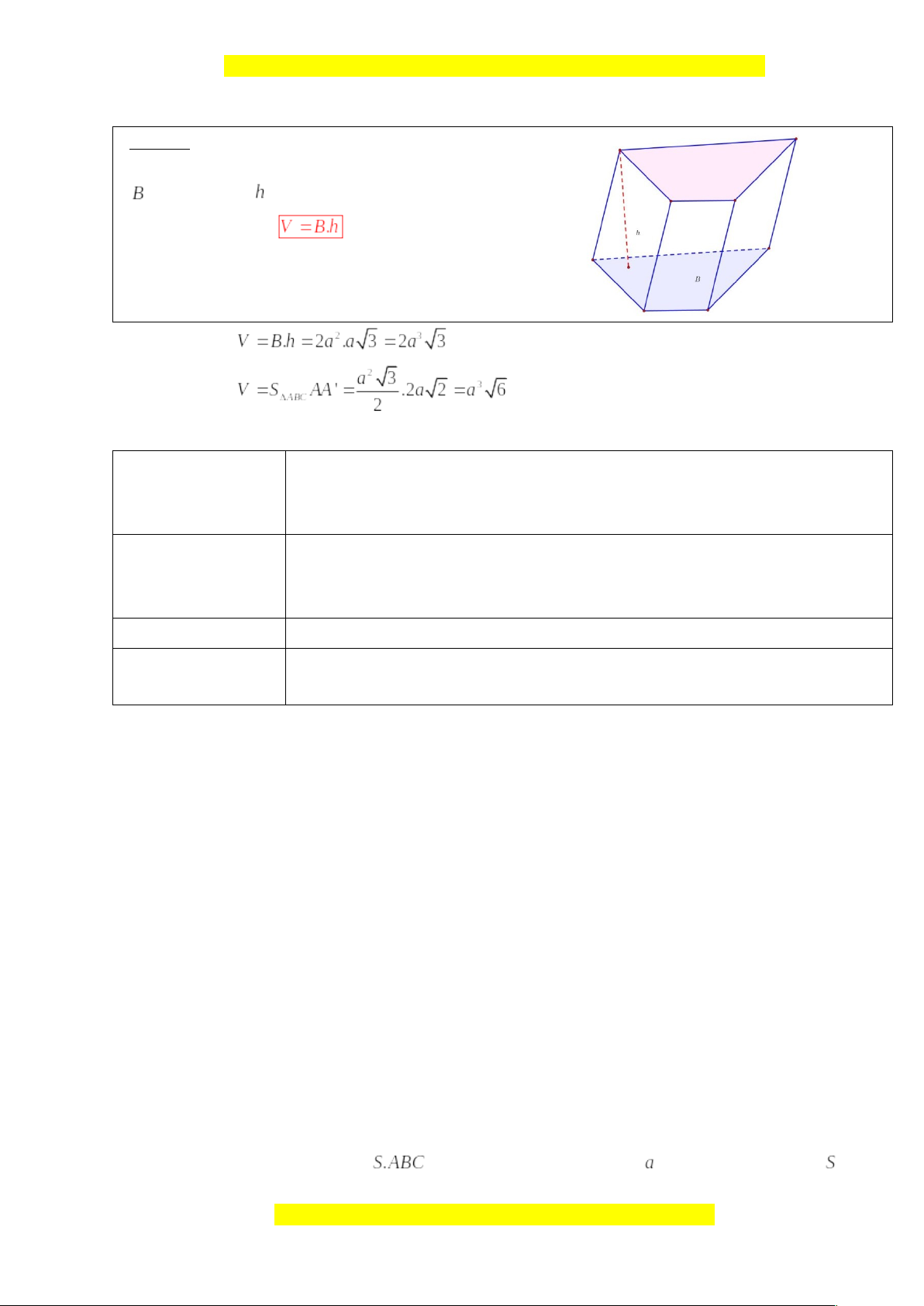
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
Định lí:
Thể tích của một khối lăng trụ có diện tích đáy
và chiều cao là:
Kết quả VD2:
Kết quả VD3:
d) Tổ chức thực hiện
Chuyển giao
a4j88/6-ECDT
P+0-&)!<[
P5
Thực hiện
a4'<7+8<2Ob
PNC888+0/+;f1CD
P+$#1$#,&O80&-&)
Báo cáo thảo luận P9<Gk<169%<5Ie
Đánh giá, nhận xét,
tổng hợp
a4I<6)<-&/kA'<*$#,
lbZPm9n%G
III. NỘI DUNG 3
a) Mục tiêu: =$%&'()$*01
Câu hỏi 1: o8$+<,)()$*01Y
Câu hỏi 2:*)()M+$*01+16In23#*Y
Câu hỏi 3:-12@11In=#M+&(&-&&f1gY
Câu hỏi 4:qn2E+M+=01//2E318+
+ Hình chóp có 1 cạnh bên vuông góc với đáy
+ Hình chóp có 2 mặt cùng vuông góc với đáy
+ Hình chóp có một mặt bên vuông góc với đáy
+ Hình chóp có các cạnh bên bằng nhau hoặc tạo với đáy những góc bằng
+ Hình chóp có các mặt bên cùng tạo với đáy những góc bằng nhau và chân đường cao thuộc miền
trong đa giác đáy
+ Hình chóp đều chân đường cao trùng với tâm của đáy.
Câu hỏi 5: N&$*-./+&<+0(+$*-./&A$*01
-+&Y()M+&H$*0107+%O+2#Yr+%2#
O()M+$*-./9+Y
Ví dụ 4:N=01+& 0-+&' <'+Ts
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Nhắn tin Zalo