Trắc nghiệm Toán 10 Cánh diều Chương 3 (có đúng sai, trả lời ngắn)

Chương III. Hàm số và đồ thị
Bài 1. Hàm số và đồ thị
Phần I. Trắc nghiệm nhiều phương án lựa chọn x  3 Câu 1.
Tập xác định của hàm số y  là 2x  2 A. \   1 . B. \   3 . C. \   2 . D. 1; .
Câu 2. Hàm số nào sau đây có tập xác định là R ? 2 x A. y 
y  x  x   . 2 x  . B. 2 2 1 3 4 3x C. y  y  x  x   . 2 x  . D. 2 2 1 3 4 2x 1
Câu 3. Với giá trị nào của m thì hàm số y  2
x  2x  3  xác định trên . m A. m  4  . B. m  4  .
C. m  0 .
D. m  4 . Câu 4.
Xét sự biến thiên của hàm số   3 f x 
trên khoảng 0; . Khẳng định nào sau đây x đúng?
A. Hàm số nghịch biến trên khoảng 0; .
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng 0; .
C. Hàm số đồng biến trên khoảng 0; .
D. Hàm số không đồng biến, không nghịch biến trên khoảng 0; . Câu 5. Cho hàm số 3
y  x  3x  2 . Điểm nào sau đây thuộc đồ thị hàm số đã cho? A.  2  ;0 . B. 1;  1 . C.  2  ; 1  2. D. 1; 1  .
Câu 6. Cho hàm số y  f  x xác định trên khoảng  ;
  có đồ thị như hình vẽ dưới đây.
Mệnh đề nào sau đây đúng?
A. Hàm số đồng biến trên khoảng 0; 2 .
B. Hàm số nghịch biến trên khoảng  3  ;0.
C. Hàm số đồng biến trên khoảng  1  ;0 .
D. Hàm số nghịch biến trên khoảng 0;  3 .
2x 1 khi x 1  Câu 7. Cho hàm số y  1
 khi 0  x 1 . Giá trị lớn nhất của hàm số trên  2  ;  2 là:
12x khi x  0  A. 2. B. 4. C. 5. D. 7. Câu 8.
Tìm giá trị nhỏ nhất của hàm số f  x  x   x  2 2 3 . 9 9 3 A. 0. B. . C. . D. . 2 2 2 Câu 9.
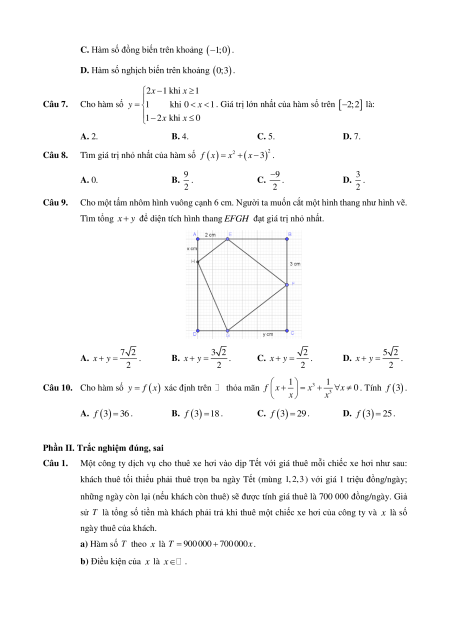
Cho một tấm nhôm hình vuông cạnh 6 cm. Người ta muốn cắt một hình thang như hình vẽ.
Tìm tổng x  y để diện tích hình thang EFGH đạt giá trị nhỏ nhất. 7 2 3 2 2 5 2
A. x  y  .
B. x  y  .
C. x  y  .
D. x  y  . 2 2 2 2  1  1
Câu 10. Cho hàm số y  f  x xác định trên thỏa mãn 3 f x   x  x   0   . Tính f   3 . 3  x  x A. f   3  36 . B. f   3  18 . C. f   3  29 . D. f   3  25 .
Phần II. Trắc nghiệm đúng, sai
Câu 1. Một công ty dịch vụ cho thuê xe hơi vào dịp Tết với giá thuê mỗi chiếc xe hơi như sau:
khách thuê tối thiểu phải thuê trọn ba ngày Tết (mùng 1, 2, 3 ) với giá 1 triệu đồng/ngày;
những ngày còn lại (nếu khách còn thuê) sẽ được tính giá thuê là 700 000 đồng/ngày. Giả
sử T là tổng số tiền mà khách phải trả khi thuê một chiếc xe hơi của công ty và x là số ngày thuê của khách.
a) Hàm số T theo x là T  900 000  700 000x .
b) Điều kiện của x là x  .
c) Một khách hàng thuê một chiếc xe hơi công ty trong 7 ngày tết thì sẽ trả khoản tiền thuê là 5800 000 (đồng).
d) Anh Bình định dành ra một khoản tối đa là 10 triệu đồng cho phí thuê xe đi chơi trong
dịp tết, khi đó anh Bình có thể thuê xe của công ty trên tối đa 12 ngày.
Câu 2. Cho biểu đồ ước tính dân số Việt Nam qua một số thập niên như sau:
Nếu coi x là năm và y là số dân Việt Nam thì x là biến số và y là hàm số của x .
a) Tập xác định của hàm số là D  1979;1989;1999;2009;201  9 .
b) Tập giá trị của hàm số là T  10;20;...;10  0 .
c) Hàm số đồng biến trên tập xác định.
d) Trong khoảng thời gian từ 1989 đến 1999 dân số Việt Nam tăng nhanh nhất.
Câu 3. Cho hàm số y  f  x  x 1 .
a) Hàm số có tập xác định là D   1  ;.
b) Điểm M 0; 
1 thuộc đồ thị hàm số. c) f   1  f   3  5 .
d) Hàm số nghịch biến trên 0; .  x 1 khi x  2 
Câu 4. Cho hàm số y  f  x  c khi x  2 .  2 1 x khi x  2 
a) f 0  1.
b) Hàm số có tập xác định là D  1;+ .
c) Biết f 2  f  
1  1, khi đó c 1.
d) Với t  x 1 thì với t  f t  2 3,  t   2t .