Bài giảng Powerpoint Toán 9 Học kì 2

120 60 lượt tải
Chia sẻ Facebook Báo cáo tài liệu
Lớp: Lớp 9
Môn: Toán Học
Dạng: Giáo án, Giáo án Powerpoint
File:
Loại: Tài liệu lẻ

CÁCH MUA:

Liên hệ ngay Hotline hỗ trợ: 0842834585

Bộ bài giảng điện tử Toán 9 được cập nhật liên tục trong gói này từ nay đến hết tháng 3/2024.  

Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!

  • Bộ bài giảng powerpoint Toán 9 mới, chuẩn nhất bao gồm đầy đủ các bài giảng cả năm. Bộ bài giảng được thiết kế theo phong cách hiện đại, đẹp mắt, trình bày chi tiết cho từng phần học và bám sát chương trình Sách giáo khoa Toán lớp 9.
  • Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.

Đánh giá

4.6 / 5(120 )
5
53%
4
22%
3
14%
2
5%
1
7%
Trọng Bình
Tài liệu hay

Giúp ích cho tôi rất nhiều

Duy Trần
Tài liệu chuẩn

Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)

TÀI LIỆU BỘ BÁN CHẠY

Xem thêm

Tài liệu bộ mới nhất

TẢI NGAY
Lớp 9 KHTN

Bộ đề thi giữa kì 1 KHTN 9 Cánh diều có đáp án


Miễn phí
16
TẢI NGAY
Lớp 9 KHTN

Bộ đề thi giữa kì 1 KHTN 9 Kết nối tri thức có đáp án


Miễn phí
16
TẢI NGAY
Lớp 9 KHTN

Bộ đề thi giữa kì 1 KHTN 9 Chân trời sáng tạo có đáp án


Miễn phí
18
TẢI NGAY
Lớp 9 GDCD

Bộ đề thi giữa kì 1 GDCD 9 Cánh diều có đáp án


Miễn phí
18
TẢI NGAY
Lớp 9 GDCD

Bộ đề thi giữa kì 1 GDCD 9 Kết nối tri thức có đáp án


Miễn phí
18
TẢI NGAY
Lớp 9 GDCD

Bộ đề thi giữa kì 1 GDCD 9 Chân trời sáng tạo có đáp án


Miễn phí
15
TẢI NGAY
Lớp 9 Sử & Địa

Bộ đề thi giữa kì 1 Lịch sử&Địa Lý 9 Cánh diều có đáp án


Miễn phí
16
TẢI NGAY
Lớp 9 Sử & Địa

Bộ đề thi giữa kì 1 Lịch sử&Địa Lý 9 Kết nối tri thức có đáp án


Miễn phí
16
TẢI NGAY
Lớp 9 Sử & Địa

Bộ đề thi giữa kì 1 Lịch sử&Địa Lý 9 Chân trời sáng tạo có đáp án


Miễn phí
16
TẢI NGAY
Lớp 9 Tin Học

Bộ đề thi giữa kì 1 Tin học 9 Cánh diều có đáp án


Miễn phí
17
CHÀO MỪNG QUÝ THẦY CÔ
VÀ CÁC EM HỌC SINH
MÔN TOÁN 9
Giáo viên: …
NOTES
Phần 2:
HÌNH THÀNH KIẾN THỨC
Phần 4:
VẬN DỤNG, TÌM TÒI
Phần 3:
LUYỆN TẬP
Phần 1: KHỞI ĐỘNG
THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Giáo viên: Thước thẳng, thước đo góc,
bảng phụ, bảng nhóm.
2. Học sinh:sách giáo khoa, tài liệu trên
mạng internet, thước thẳng, bảng nhóm.
Bài
1
Phương
trình
bậc
nhất
ẩn
Bài
2
2
Hệ
hai
phương
trình
bậc
nhất
hai
ẩn
Bài
3
3
Giải
hệ
phương
trình
bằng
phương
pháp
thế
Bài
4
Giải
hệ
phương
trình
bằng
phương
pháp
cộng
đại
số
Bài
5
Giải
bài
toán
bằng
cách
lập
hệ
phương
trình
Hệ hai phương trình bậc nhất hai ẩn
KHỞI ĐỘNG
TRÒ CHƠI: VƯỢT CHƯỚNG NGẠI VẬT (Lật hình)
1
2
3
4
Luật chơi: Chọn ngẫu
nhiên 1 câu hỏi. Trả lời
đúng thì ô tương ứng với
câu hỏi sẽ được mở ra,
trường hợp trả lời sai thì
ô tương ứng không được
mở. Bất kỳ khi nào có
câu trả lời về bức hình
đều có thể trả lời. Trò
chơi sẽ kết thúc khi hình
ảnh sau các miếng ghép
được trả lời chính xác.
ĐÃ HIỂU
2 4 5xy+=
TRÒ CHƠI: VƯỢT CHƯỚNG NGẠI VẬT (Lật hình)
HÌNH ẢNH
1
2
3 4
1 2
3
4
1 2
3 4
Luật chơi: Chọn ngẫu
nhiên 1 câu hỏi. Trả lời
đúng thì ô tương ứng
với câu hỏi sẽ được mở
ra, trường hợp trả lời
sai thì ô tương ứng
không được mở. Bất kỳ
khi nào có câu trả lời
về bức hình đều có thể
trả lời. Trò chơi sẽ kết
thúc khi hình ảnh sau
các miếng ghép được
trả lời chính xác.
TRÒ CHƠI: VƯỢT CHƯỚNG NGẠI VẬT
1
Phương trình nào sau đây là phương trình
bậc nhất một ẩn?
A.
B:
C:
D:
2 3 5xy+=
0 3 5x+=
2
30
x
+=
2 3 0x+=
QUAY LẠI
C.
B:
A:
D: Vô nghiệm
TRÒ CHƠI: VƯỢT CHƯỚNG NGẠI VẬT
2
Nghiệm của phương trình là
5x=
1x=
1x=−
QUAY LẠI
2 4 6x+=
A.
B:
C:
D:
TRÒ CHƠI: VƯỢT CHƯỚNG NGẠI VẬT
3
QUAY LẠI
Phương trình tương đương với
phương trình là:
23x+=
23x−=
23x+ = −
2 4 3x+=
2 4 6x+=
D. Một nghiệm duy nhất
B: Có vố số nghiệm
C: Có 2 nghiệm phân biệt
A: Vô nghiệm
TRÒ CHƠI: VƯỢT CHƯỚNG NGẠI VẬT
4
QUAY LẠI
Phương trình có tất cả bao nhiêu nghiệm?
2 4 6x+=
HÌNH THÀNH
KIẾN THỨC
TIẾT 30: PHƯƠNG TRÌNH
BẬC NHẤT HAI ẨN
- Nắm được khái niệm
phương trình bậc nhất hai ẩn,
nghiệm và cách giải phương
trình bậc nhất 2 ẩn
- Liên hệ với phương trình
bậc nhất một ẩn.
- Biết cách tìm
công thức nghiệm
tổng quát và vẽ
đường thẳng biểu
diễn tập nghiệm
của một phương
trình bậc nhất hai
ẩn.
PHƯƠNG TRÌNH BẬC
NHẤT HAI ẨN
là phương trình bậc nhất hai ẩn
2 4 5xy+=
Phương trình bậc nhất hai ẩn có
dạng như thế nào?
Ví dụ : Phương trình bậc nhất hai ẩn:
1. Khái niệm về phương trình bậc nhất hai ẩn.
2 5 3xy− + =
0 3 5xy−=
2 0 0,2xy+=
Phương trình bậc nhất hai ẩn x, y là hệ thức có dạng
trong đó 𝒂, 𝒃, 𝒄 là các số đã biết ( hoặc )
(1)ax by c+=
0a
0b
( )
2; 5; 3a b c=− = =
( )
0; 3; 5= =− =a b c
( )
2; 0; 0,2a b c= = =
( )
1: 0; 0TH ax by c a b+ =
( )
2: 0 0; 0TH x by c a b+ = =
( )
3: 0 0; 0TH ax y c a b+ = =
Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Trong các phương trình sau, phương trình nào là
phương trình bậc nhất 2 ẩn? Hãy xác định hệ số a, b, c?
( )
( )
( )
( )
( )
2
1 5 4
2 3 5
3 4 0 0
4 0 0 7
5 0 4
yx
xy
xy
xy
xy
− = −
+=
+=
+=
+=
( )
1; 4; 5a b c=− = =−
( )
4; 0; 0a b c= = =
( )
0; 1; 4a b c= = =
01:0000:5900:5800:5700:5600:5500:5400:5300:5200:5100:5000:4900:4800:4700:4600:4500:4400:4300:4200:4100:4000:3900:3800:3700:3600:3500:3400:3300:3200:3100:3000:2900:2800:2700:2600:2500:2400:2300:2200:2100:2000:1900:1800:1700:1600:1500:1400:1300:1200:1100:1000:0900:0800:0700:0600:0500:0400:0300:0200:0100:00
Xét phương trình:
NV2: Thay giá trị 𝑥 = 1 và 𝑦 = 2 vào vế trái của
phương trình (1) rồi so sánh giá trị của vế trái và vế phải
của phương trình.
NV1: Thay giá trị 𝑥 = 3 và 𝑦 = 5 vào vế trái của
phương trình (1) rồi so sánh giá trị của vế trái và vế phải
của phương trình.
( )
2 1 1xy−=
01:0000:5900:5800:5700:5600:5500:5400:5300:5200:5100:5000:4900:4800:4700:4600:4500:4400:4300:4200:4100:4000:3900:3800:3700:3600:3500:3400:3300:3200:3100:3000:2900:2800:2700:2600:2500:2400:2300:2200:2100:2000:1900:1800:1700:1600:1500:1400:1300:1200:1100:1000:0900:0800:0700:0600:0500:0400:0300:0200:0100:00
Thay 𝑥 = 3 và 𝑦 = 5 vào
vế trái của phương trình (1)
ta có:
Cặp số (3; 5) là một nghiệm
của phương trình (1)
Thay 𝑥 = 1 và 𝑦 = 2 vào
vế trái của phương trình (1)
ta có:
Cặp số (1; 2) không là nghiệm
của phương trình (1)
Xét phương trình:
( )
2 1 1xy−=
2.3 5 1
1
VT
VP
VT VP
= − =
=
=
2.1 2 0
1
VT
VP
VT VP
= − =
=

*Kết luận:
Trong phương trình , nếu giá trị của vế trái
tại 𝒙 = 𝒙
𝟎
và 𝐲 = 𝒚
𝟎
bằng vế phải thì cặp số 𝒙
𝟎
; 𝒚
𝟎
được gọi là một nghiệm của phương trình
ax by c+=
Khi nào cặp số (x
0
; y
0
)
được gọi là một nghiệm của
phương trình ax + by = c ?
a) Kiểm tra xem cặp số (1;1) và (0,5;0) có là nghiệm của
phương trình hay không?
b) Tìm thêm một nghiệm khác của phương trình:
?1(SGK/5)
Nêu nhận xét về số nghiệm của phương trình
21xy−=
21xy−=
21xy−=
?2(SGK/5)
02:0001:5901:5801:5701:5601:5501:5401:5301:5201:5101:5001:4901:4801:4701:4601:4501:4401:4301:4201:4101:4001:3901:3801:3701:3601:3501:3401:3301:3201:3101:3001:2901:2801:2701:2601:2501:2401:2301:2201:2101:2001:1901:1801:1701:1601:1501:1401:1301:1201:1101:1001:0901:0801:0701:0601:0501:0401:0301:0201:0101:0000:5900:5800:5700:5600:5500:5400:5300:5200:5100:5000:4900:4800:4700:4600:4500:4400:4300:4200:4100:4000:3900:3800:3700:3600:3500:3400:3300:3200:3100:3000:2900:2800:2700:2600:2500:2400:2300:2200:2100:2000:1900:1800:1700:1600:1500:1400:1300:1200:1100:1000:0900:0800:0700:0600:0500:0400:0300:0200:01
00:00
?1(SGK/5)
21xy−=
21xy−=
+) Thay 𝑥 = 1 và 𝑦 = 1 vào vế trái của phương trình
ta có:
Cặp số (1 ; 1) là một nghiệm của phương trình
2.1 1 1
1
VT
VP
VT VP
= − =
=
=
21xy−=
+) Thay 𝑥 = 0,5 và 𝑦 = 0 vào vế trái của phương trình
ta có:
Cặp số (0,5 ; 0) là một nghiệm của phương trình
2.0,5 0 1
1
VT
VP
VT VP
= − =
=
=
21xy−=
?2(SGK/5)
Phương trình có vô số nghiệm
21xy−=
2. Tập nghiệm của phương trình bậc nhất hai ẩn:
Xét phương trình
( )
2 1 2xy−=
21yx = −
Điền vào bảng sau và viết ra sáu nghiệm của phương trình (2)
?3(SGK/5)
x − 𝟏 𝟎 𝟎, 𝟓 𝟏 𝟐 𝟐, 𝟓
y = 2x -1
Sáu nghiệm của phương trình (2) là:
𝟎− 𝟏 𝟏
𝟑
𝟒− 𝟑
( )
31; ;− −
( )
0; ;1−
( )
0,5;0 ;
( )
1;1 ;
( )
2;3 ;
( )
2,5;4
- Nghiệm tổng quát là :
với
- Tập nghiệm của phương trình (2) là :
( )
;2 1 /S x x x R= −
21
xR
yx
=−
xR
hoặc
( )
;2 1xx−
Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
Trong mặt phẳng toạ độ Oxy, tập hợp các điểm biểu diễn các
nghiệm của phương trình (2) là đường thẳng y = 2x – 1
- Tập nghiệm của (2) được biểu
diễn bởi đường thẳng (d): y = 2x –1
Hay đường thẳng (d) được xác định
bởi phương trình 2x – y = 1
Đường thẳng (d) còn gọi là đường
thẳng 2x – y = 1 và được viết gọn
là : (d) : 2x – y = 1
2,5
0,5
-3
-3
-2
-1
-2
-1
4
3
2
1
4
3
2
1
y
x
O
(-1;-3)
(0;-1)
(0,5;0)
(1;1)
(2,5;4)
(2;3)
(d)
1. Khái niệm về phương trình bậc nhất hai ẩn.
2. Tập nghiệm của phương trình bậc nhất hai ẩn:
Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Khái niệm về phương trình bậc nhất hai ẩn.
2. Tập nghiệm của phương trình bậc nhất hai ẩn:
Nghiệm TQ:
+−=
b
c
x
b
a
y
Rx
( )
0; 0abax by c +=
by ax c =− +
ac
x
bb
y
−
+=
Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
hoặc
2. Tập nghiệm của phương trình bậc nhất hai ẩn:
- Xét phương trình:
y = 2
- Xét phương trình
1. Khái niệm về phương trình bậc nhất hai ẩn:
(0;2)
-3
-3
-2
-1
-2
-1
4
3
2
1
4
3
2
1
y
x
O
A
(1,5;0)
-3
-3
-2
-1
-2
-1
4
3
2
1
4
3
2
1
y
x
B
O
Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
( )
0 2 4 3xy+=
24
2
y
y
=
=
Nghiệm TQ:
=
2y
Rx
𝑥 = 1,5
Nghiệm TQ:
=
Ry
x 5,1
( )
4 0 6 4xy+=
46
1,5
x
x
=
=
PT bậc nhất hai ẩn CT nghiệm TQ Minh hoạ tập nghiệm
Tổng quát
0;
c
b



;0
c
a



Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
+−=
b
c
x
b
a
y
Rx
=
Ry
a
c
x
=
b
c
y
Rx
( )
0; 0ab
ax by c

+=
( )
0; 0
0
ab
x by c
=
+=
( )
0; 0
0
ab
ax y c
=
+=
PT bậc nhất 2 ẩn
Dạng TQ
Số nghiệm
Cấu trúc
nghiệm
Công thức
nghiệm
(a, b, c là số cho trước;
a ≠ 0 hoặc b ≠ 0)
(a, b là số cho trước;
a ≠ 0)
1 nghiệm
duy nhất
Vô số nghiệm
Là 1 số
Là một cặp số
b
x
a
−
=
PT bậc nhất 1 ẩn
Vậy da vào nhng đặc điểm nào đê
phân biệt phương trình bậc nhất một
ẩn vi phương trình bậc nhất hai ẩn?
xR
ac
yx
bb
= − +
Bài 1: PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
0ax b+=
ax by c+=
LUYỆN TẬP
Tìm công thức
nghiệm tổng quát của
phương trình:
( )
5 4 8 *xy+=
02:0001:5901:5801:5701:5601:5501:5401:5301:5201:5101:5001:4901:4801:4701:4601:4501:4401:4301:4201:4101:4001:3901:3801:3701:3601:3501:3401:3301:3201:3101:3001:2901:2801:2701:2601:2501:2401:2301:2201:2101:2001:1901:1801:1701:1601:1501:1401:1301:1201:1101:1001:0901:0801:0701:0601:0501:0401:0301:0201:0101:0000:5900:5800:5700:5600:5500:5400:5300:5200:5100:5000:4900:4800:4700:4600:4500:4400:4300:4200:4100:4000:3900:3800:3700:3600:3500:3400:3300:3200:3100:3000:2900:2800:2700:2600:2500:2400:2300:2200:2100:2000:1900:1800:1700:1600:1500:1400:1300:1200:1100:1000:0900:0800:0700:0600:0500:0400:0300:0200:0100:00
Nghiệm TQ của PT:
+
−
=
Ry
yx
5
8
5
4
Nghiệm TQ của PT:
+
−
=
2
4
5
xy
Rx
( )
5 4 8 *
5 4 8
48
55
xy
xy
xy
+=
=− +
−
= +
( )
5 4 8 *
4 5 8
5
2
4
xy
yx
xy
+=
= − +
−
= +
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Diophantus xứ Alexandria
Tr
o
chơi
gi
ả
i
m
ã
b
ứ
c
tranh
Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?
Sai
Sai
Đng
Sai
A
B
C
D
2
2 3 0xy+=
3
5xy+=
2 3 4xy−=
1xy x−=
Câu 2: Đường thẳng (d) trên hình vẽ sau biểu diễn tập nghiệm của
phương trình nào ?
A
2xy−=
B
C
Đng
Sai
Sai
2xy+=
2xy− = −
3
2
1
1
4
3
(d)
x
y
4
2
O
Câu 3: Cặp sô (– 2; 1) là nghiệm của phương trình nào trong
các phương trình sau ?
A
25xy−=
B
C
Đng
Sai
Sai
D
Sai
31xy+=
53xy+ = −
35xy−=
Câu 4: Công thức nghiệm tổng quát của phương trình
là
Sai
Đúng
Sai
Sai
A
B
C
D
4 0 4xy+=
1x =
1x
yR
=
1xy+=
yR
Bạn Phương Anh:
Câu 5: Bạn Lan va bạn Phương Anh khi tìm nghiệm tổng quát của
phương trình 3x – y = 2 đa đưa ra các kết quả như sau:
Bạn Lan:
x
y 3x 2
R
=−
12
xy
33
y R
=+
A
Ch có bạn Lan đúng.
B
C
Ch có bạn Phương Anh đúng.
Cả Lan va Phương Anh đều đúng.
Sai
Sai
Đúng
CỦNG CỐ
Bài tập thực tế
Bài toán:
Số tiền mua 9 quả hồng và 8 quả táo là 107 nghìn
đồng. Số tiền mua 7 quả hồng và 7 quả táo là 91
nghìn đồng. Hãy lập các phương trình cho bài toán
trên.
Hướng dẫn: Gọi giá tiền mỗi quả hồng là x, giá tiền mỗi
quả táo là y thì ta có phương trình: và
phương trình là các phương trình bậc nhất
hai ẩn.
7 7 91xy+=
9 8 107xy+=
Bài tập: Tìm nghiệm nguyên của phương trình:
)3 2 5
) 42
a x y
b x y
+=
+=
TÌM TÒI MỞ RỘNG
Phương trình bậc nhất hai ẩn:
Trong đó a, b, c là các sô đã biết;
hoặc
Tập nghiệm biểu diễn bởi
đường thẳng:
Luôn có vô sô nghiệm
Biểu diễn tập nghiệm
Biểu diễn tập nghiệm Biểu diễn tập nghiệm
Nghiệm tổng quát
Nghiệm tổng quát
Nghiệm tổng quát
xR
ac
yx
bb
= − +
bc
xy
aa
yR
= − +
c
x
a
yR
=
xR
c
y
b
=
ax by c+=
ax by c+=
( )
0; 0ab
( )
00ab
và
( )
00ab=
và
( )
00ab=
và
ax by c+=
0ax y c+=
0x by c+=
• Nắm vững định nghĩa, nghiệm, số nghiệm của
phương trình bậc nhất hai ẩn. Biết viết nghiệm tổng
quát và biểu diễn tập nghiệm trên mặt phẳng toạ độ.
• Đọc mục “Có thể em chưa biết” SGK T/8
• Làm bài tập1;2 ;3 SGK và bài tập vận dụng.
HƯỚNG DẪN VỀ NHÀ
Diofantus xứ
Alexandria
khong năm 250

Mô tả nội dung:


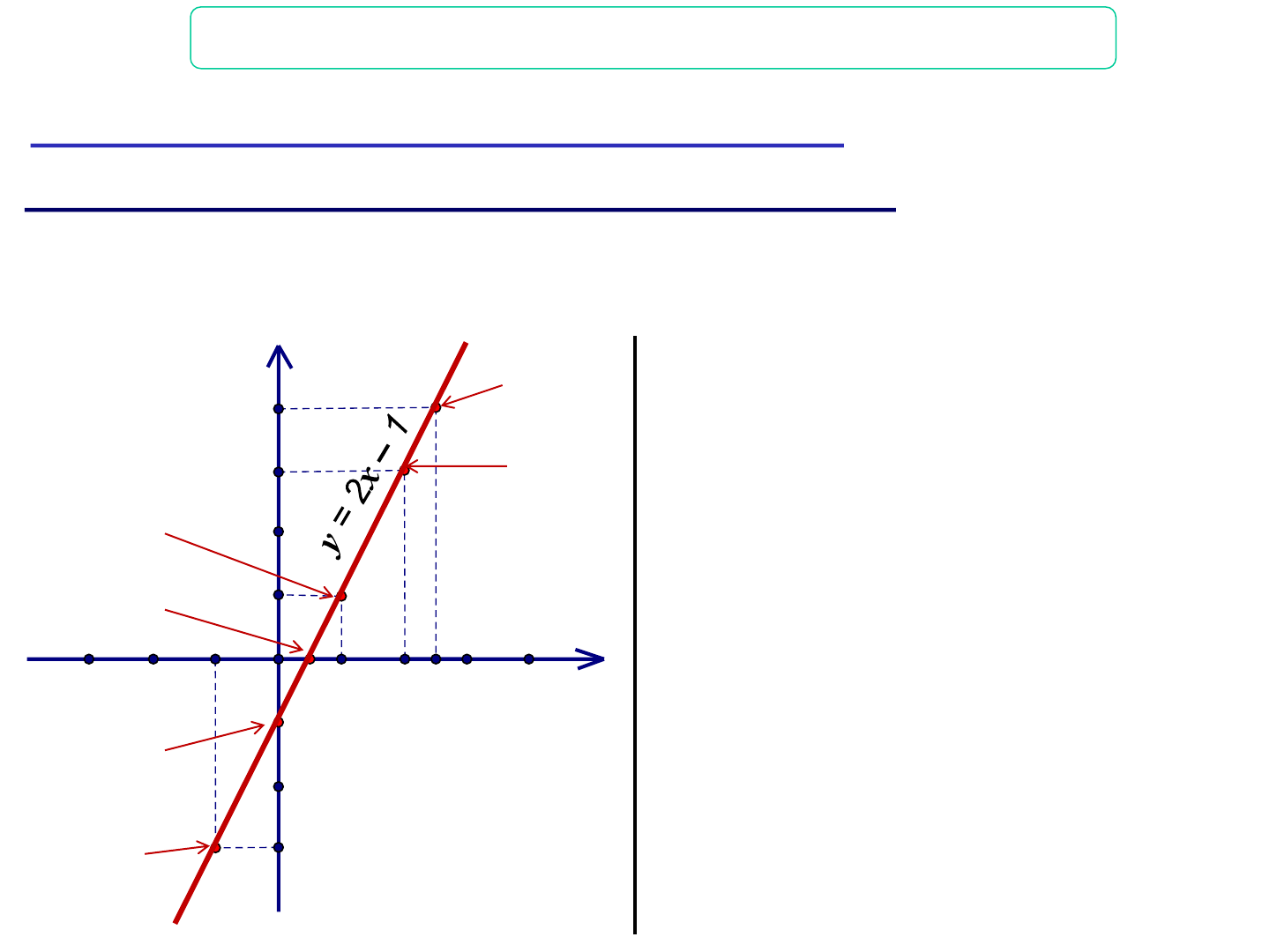
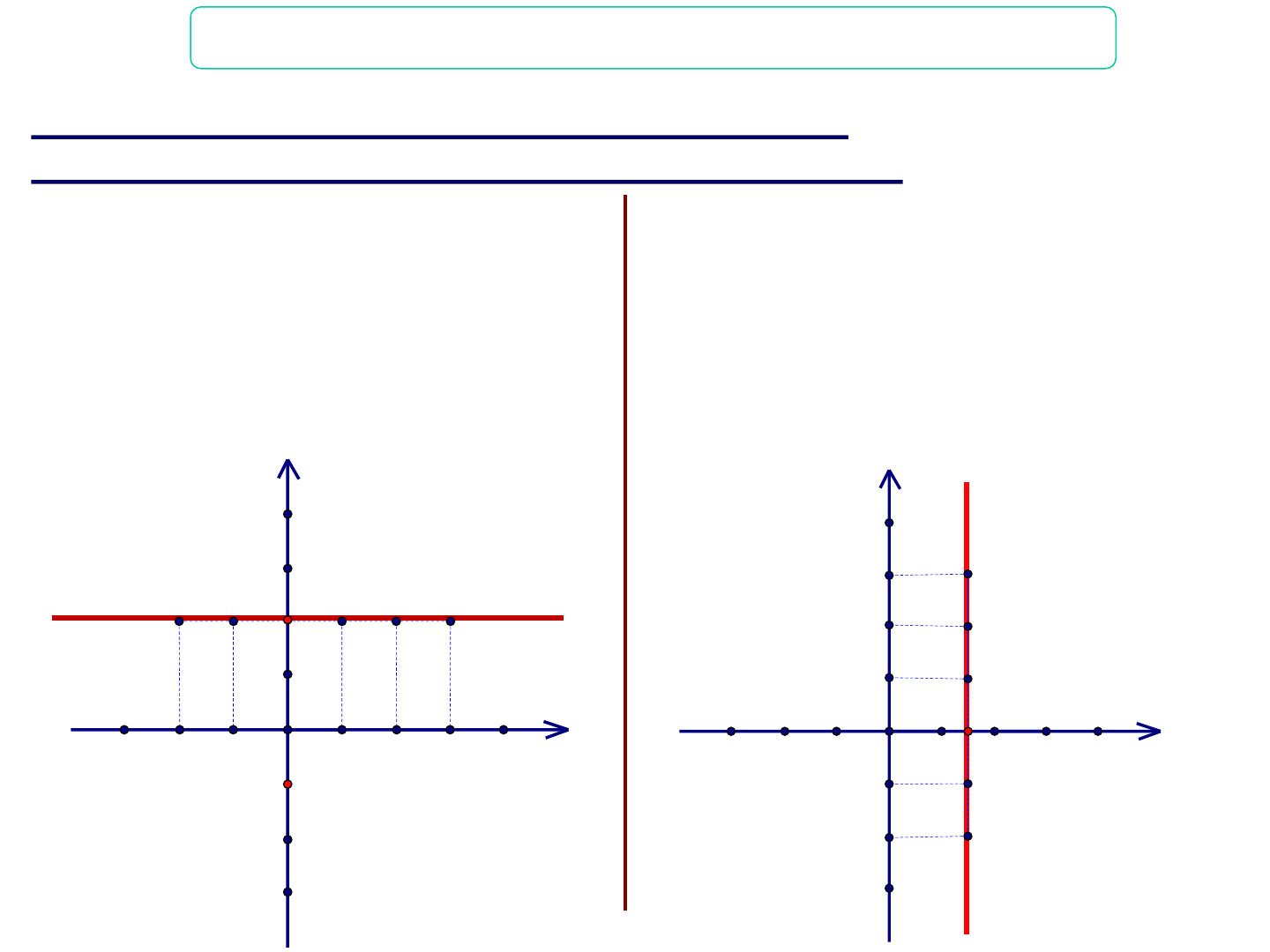
CHÀO MỪNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH MÔN TOÁN 9 Giáo viên: … S OTE N
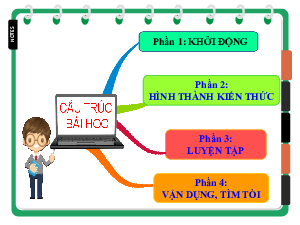
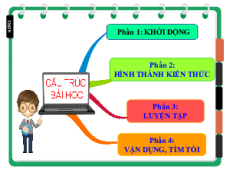
Phần 1: KHỞI ĐỘNG Phần 2:
HÌNH THÀNH KIẾN THỨC Phần 3: LUYỆN TẬP Phần 4: VẬN DỤNG, TÌM TÒI
THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Giáo viên: Thước thẳng, thước đo góc,
bảng phụ, bảng nhóm.
2. Học sinh:sách giáo khoa, tài liệu trên
mạng internet, thước thẳng, bảng nhóm.
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27
  • Slide 28
  • Slide 29
  • Slide 30
  • Slide 31
  • Slide 32
  • Slide 33
  • Slide 34
  • Slide 35
  • Slide 36
  • Slide 37
  • Slide 38
  • Slide 39
  • Slide 40:
  • Slide 41
  • Slide 42
  • Slide 43
  • Slide 44
  • Slide 45

zalo Nhắn tin Zalo