CHƯƠNG 2 TỔ HỢP XÁC SUẤT
BÀI 1. QUY TẮC ĐẾM – HOÁN VỊ - CHỈNH HỢP – TỔ HỢP Mục tiêu Kiến thức
+ Nắm vững quy tắc cộng, quy tắc nhân.
+ Hiểu và phân biệt được các khái niệm: Hoán vị, chỉnh hợp, tổ hợp. Kĩ năng
+ Vận dụng được quy tắc cộng và nhân cho các bài toán đếm.
+ Giải được các dạng toán đếm liên quan đến tổ hợp, chỉnh hợp.
+ Giải được phương trình liên quan đến công thức tổ hợp, chỉnh hợp. Trang 1
I. LÍ THUYẾT TRỌNG TÂM
1. Các quy tắc đếm
Mở rộng: Một công việc được hoàn thành a) Quy tắc cộng bởi một trong phương án Định nghĩa
Nếu phương án có
Một công việc nào đó có thể được thực hiện theo một cách thực hiện, phương án có cách
trong hai phương án hoặc . Nếu phương án có
cách thực hiện, phương án có cách thực hiện và thực hiện,…phương án có cách thực
không trùng với bất kì cách nào trong phương án thì hiện và các cách thực hiện của các phương công việc đó có cách thực hiện.
án trên không trùng nhau thì công việc đó Công thức có cách thực hiện. Nếu
là các tập hợp không giao nhau thì Cho các tập
đôi một rời nhau. Khi đó: b) Quy tắc nhân Định nghĩa
Một công việc nào đó có thể bao gồm hai công đoạn và Mở rộng: Một công việc được hoàn thành
. Nếu công đoạn có cách thực hiện và ứng với mỗi bởi hành động liên tiếp.
cách đó có cách thực hiện công đoạn thì công việc đó có cách thực hiện.
Nếu hành động có cách thực hiện, Công thức hành động có
cách thực hiện,..., Nếu
là các tập hữu hạn phần tử thì hành động có
cách thực hiện thì công việc đó có cách hoàn 2. Hoán vị thành. Định nghĩa Cho các tập
hữu hạn phần tử.
Một tập hợp gồm phần tử Mỗi cách sắp xếp Khi đó:
phần tử theo một thứ tự được gọi là một hoán vị của phần tử.
Số hoán vị của phần tử là: Quy ước: Hoán vị lặp Cho phần tử khác nhau Mỗi cách sắp xếp
phần tử trong đó gồm phần tử phần tử phần tử
theo một thứ tự được gọi là ( với ).
một hoán vị lặp cấp kiểu của phần tử. Trang 2
Số hoán vị lặp cấp kiểu của phần tử là: (với ). Hoán vị vòng quanh
Cho tập gồm phần tử. Mỗi cách sắp xếp phần tử
của tập thành một dãy kín được gọi là một hoán vị vòng quanh của n phần tử.
Số hoán vị vòng quanh của n phần tử là: 3. Chỉnh hợp Định nghĩa
Cho tập hợp gồm phần tử. Mỗi cách sắp xếp phần tử của
theo một thứ tự được gọi là một chỉnh
hợp chập của phần tử của tập .
Số chỉnh hợp chập của phần tử:
Công thức này đúng cho trường hợp hoặc Khi thì Chỉnh hợp lặp
Cho tập gồm phần tử. Một dãy gồm phần tử của
, trong đó mỗi phần tử có thể được lặp lại nhiều lần,
được sắp xếp theo một thứ tự nhất định được gọi là một
chỉnh hợp lặp chập của phần tử của tập
Số chỉnh hợp lặp chập của phần tử: . 4. Tổ hợp Định nghĩa
Cho tập gồm phần tử. Mỗi tập con gồm Quy ước:
phần tử của được gọi là một tổ hợp chập của phần Phân biệt chỉnh hợp và tổ hợp tử.
Chỉnh hợp và tổ hợp liên hệ nhau bởi công
Số tổ hợp chập của phần tử: thức:
+ Chỉnh hợp: có thứ tự. Tính chất
+ Tổ hợp: không có thứ tự.
+ Những bài toán mà kết quả phụ thuộc vào
vị trí các phần tử ta dùng chỉnh hợp. Ngược Trang 3 lại, là tổ hợp.
Cách lấy phần tử từ tập phần tử
+ Không thứ tự, không hoàn lại: Tổ hợp lặp
+ Có thứ tự, không hoàn lại: Cho tập
và số tự nhiên bất kì. Một tổ + Có thứ tự, có hoàn lại:
hợp lặp chập của phần tử là một tập hợp gồm phần
tử, trong đó mỗi phần tử là một trong phần tử của .
Số tổ hợp lặp chập của phần tử:
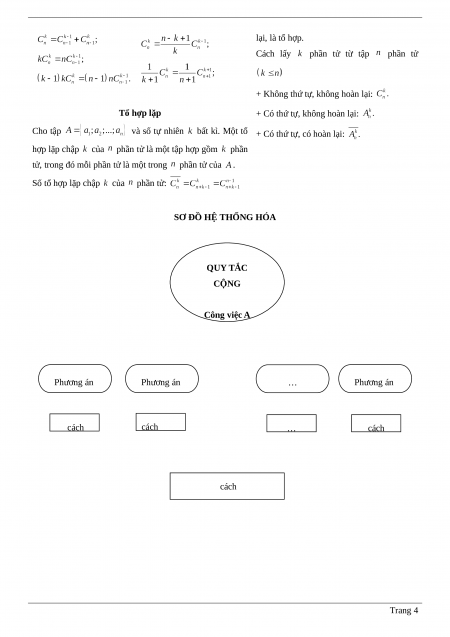
SƠ ĐỒ HỆ THỐNG HÓA QUY TẮC CỘNG Công việc A Phương án Phương án … Phương án cách cách … cách cách Trang 4
Chuyên đề Đại số và giải tích Toán 11 năm 2023 - Chương 2: Tổ hợp xác suất
605
303 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Tài liệu được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ chuyên đề Đại số và giải tích môn Toán 11 năm 2023 - Chương 2: Tổ hợp xác suất bao gồm: Bài 1: Quy tắc điểm - Hoán vị - Chỉnh hợp - Tổ hợp ; Bài 2: Nhị thức Niuton; Bài 3: Xác Suất mới nhất năm 2022 - 2023 nhằm giúp Giáo viên có thêm tài liệu tham khảo chuyên đề luyện thi Toán lớp 11.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(605 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 11
Xem thêmTài liệu bộ mới nhất

CHƯƠNG 2
TỔ HỢP XÁC SUẤT
BÀI 1. QUY TẮC ĐẾM – HOÁN VỊ - CHỈNH HỢP – TỔ HỢP
Mục tiêu
Kiến thức
+ Nắm vững quy tắc cộng, quy tắc nhân.
+ Hiểu và phân biệt được các khái niệm: Hoán vị, chỉnh hợp, tổ hợp.
Kĩ năng
+ Vận dụng được quy tắc cộng và nhân cho các bài toán đếm.
+ Giải được các dạng toán đếm liên quan đến tổ hợp, chỉnh hợp.
+ Giải được phương trình liên quan đến công thức tổ hợp, chỉnh hợp.
Trang 1

I. LÍ THUYẾT TRỌNG TÂM
1. Các quy tắc đếm
a) Quy tắc cộng
Định nghĩa
Một công việc nào đó có thể được thực hiện theo một
trong hai phương án hoặc . Nếu phương án có
cách thực hiện, phương án có cách thực hiện và
không trùng với bất kì cách nào trong phương án thì
công việc đó có cách thực hiện.
Công thức
Nếu là các tập hợp không giao nhau thì
b) Quy tắc nhân
Định nghĩa
Một công việc nào đó có thể bao gồm hai công đoạn và
. Nếu công đoạn có cách thực hiện và ứng với mỗi
cách đó có cách thực hiện công đoạn thì công việc đó
có cách thực hiện.
Công thức
Nếu là các tập hữu hạn phần tử thì
2. Hoán vị
Định nghĩa
Một tập hợp gồm phần tử Mỗi cách sắp xếp
phần tử theo một thứ tự được gọi là một hoán vị của
phần tử.
Số hoán vị của phần tử là:
Hoán vị lặp
Cho phần tử khác nhau Mỗi cách sắp xếp
phần tử trong đó gồm phần tử phần tử
phần tử theo một thứ tự được gọi là
một hoán vị lặp cấp kiểu của phần tử.
Mở rộng: Một công việc được hoàn thành
bởi một trong phương án
Nếu phương án có
cách thực hiện, phương án có cách
thực hiện,…phương án có cách thực
hiện và các cách thực hiện của các phương
án trên không trùng nhau thì công việc đó
có cách thực hiện.
Cho các tập đôi một rời nhau.
Khi đó:
Mở rộng: Một công việc được hoàn thành
bởi hành động liên tiếp.
Nếu hành động có cách thực hiện,
hành động có cách thực hiện,...,
hành động có cách thực hiện thì
công việc đó có cách hoàn
thành.
Cho các tập hữu hạn phần tử.
Khi đó:
Quy ước:
( với ).
Trang 2

Số hoán vị lặp cấp kiểu của phần tử là:
Hoán vị vòng quanh
Cho tập gồm phần tử. Mỗi cách sắp xếp phần tử
của tập thành một dãy kín được gọi là một hoán vị vòng
quanh của n phần tử.
Số hoán vị vòng quanh của n phần tử là:
3. Chỉnh hợp
Định nghĩa
Cho tập hợp gồm phần tử. Mỗi cách sắp xếp phần
tử của theo một thứ tự được gọi là một chỉnh
hợp chập của phần tử của tập .
Số chỉnh hợp chập của phần tử:
Chỉnh hợp lặp
Cho tập gồm phần tử. Một dãy gồm phần tử của
, trong đó mỗi phần tử có thể được lặp lại nhiều lần,
được sắp xếp theo một thứ tự nhất định được gọi là một
chỉnh hợp lặp chập của phần tử của tập
Số chỉnh hợp lặp chập của phần tử: .
4. Tổ hợp
Định nghĩa
Cho tập gồm phần tử. Mỗi tập con gồm
phần tử của được gọi là một tổ hợp chập của phần
tử.
Số tổ hợp chập của phần tử:
Tính chất
(với ).
Công thức này đúng cho trường hợp
hoặc
Khi thì
Quy ước:
Phân biệt chỉnh hợp và tổ hợp
Chỉnh hợp và tổ hợp liên hệ nhau bởi công
thức:
+ Chỉnh hợp: có thứ tự.
+ Tổ hợp: không có thứ tự.
+ Những bài toán mà kết quả phụ thuộc vào
vị trí các phần tử ta dùng chỉnh hợp. Ngược
Trang 3
Tổ hợp lặp
Cho tập và số tự nhiên bất kì. Một tổ
hợp lặp chập của phần tử là một tập hợp gồm phần
tử, trong đó mỗi phần tử là một trong phần tử của .
Số tổ hợp lặp chập của phần tử:
lại, là tổ hợp.
Cách lấy phần tử từ tập phần tử
+ Không thứ tự, không hoàn lại:
+ Có thứ tự, không hoàn lại:
+ Có thứ tự, có hoàn lại:
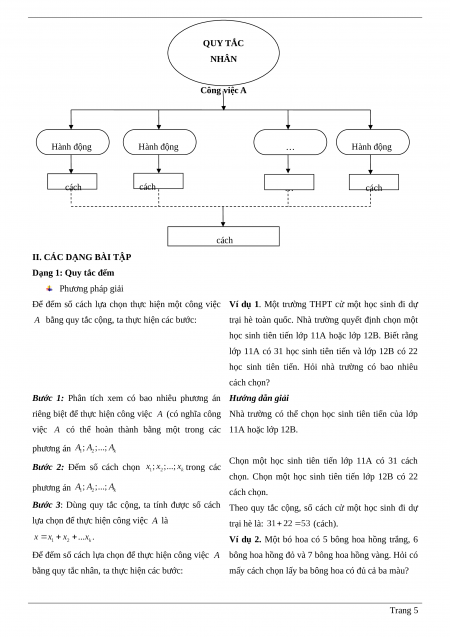
SƠ ĐỒ HỆ THỐNG HÓA
Trang 4
QUY TẮC
CỘNG
Công việc A
Phương án Phương án
…
Phương án
cách
cách
… cách
cách
II. CÁC DẠNG BÀI TẬP
Dạng 1: Quy tắc đếm
Phương pháp giải
Để đếm số cách lựa chọn thực hiện một công việc
bằng quy tắc cộng, ta thực hiện các bước:
Bước 1: Phân tích xem có bao nhiêu phương án
riêng biệt để thực hiện công việc (có nghĩa công
việc có thể hoàn thành bằng một trong các
phương án
Bước 2: Đếm số cách chọn trong các
phương án
Bước 3: Dùng quy tắc cộng, ta tính được số cách
lựa chọn để thực hiện công việc là
Để đếm số cách lựa chọn để thực hiện công việc
bằng quy tắc nhân, ta thực hiện các bước:
Ví dụ 1. Một trường THPT cử một học sinh đi dự
trại hè toàn quốc. Nhà trường quyết định chọn một
học sinh tiên tiến lớp 11A hoặc lớp 12B. Biết rằng
lớp 11A có 31 học sinh tiên tiến và lớp 12B có 22
học sinh tiên tiến. Hỏi nhà trường có bao nhiêu
cách chọn?
Hướng dẫn giải
Nhà trường có thể chọn học sinh tiên tiến của lớp
11A hoặc lớp 12B.
Chọn một học sinh tiên tiến lớp 11A có 31 cách
chọn. Chọn một học sinh tiên tiến lớp 12B có 22
cách chọn.
Theo quy tắc cộng, số cách cử một học sinh đi dự
trại hè là: (cách).
Ví dụ 2. Một bó hoa có 5 bông hoa hồng trắng, 6
bông hoa hồng đỏ và 7 bông hoa hồng vàng. Hỏi có
mấy cách chọn lấy ba bông hoa có đủ cả ba màu?
Trang 5
QUY TẮC
NHÂN
Công việc A
Hành động Hành động
…
Hành động
cách
cách
… cách
cách