Đề cương Giữa kì 1 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận)

Đề cương giữa học kì I
Môn Toán lớp 12 – Kết nối tri thức và cuộc sống I. NỘI DUNG ÔN TẬP
Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Bài 1. Tính đơn điệu và cực trị của hàm số
- Tính đơn điệu của hàm số: Khái niệm, sử dụng bảng biến thiên xét tính đơn điệu của hàm số.
- Cực trị của hàm số: Khái niệm, cách tìm cực trị.
Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Định nghĩa giá trị lớn nhất, giá trị nhỏ nhất.
- Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn.
Bài 3. Đường tiệm cận của đồ thị hàm số
- Đường tiệm cận ngang.
- Đường tiệm cận đứng.
- Đường tiệm cận xiên.
Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
- Sơ đồ khảo sát hàm số.
- Khảo sát và vẽ đồ thị hàm số đa thức bậc ba.
- Khảo sát và vẽ đồ thị hàm số phân thức hữu tỉ.
Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
- Tốc độ thay đổi của một đại lượng.
- Một vài bài toán tối ưu hóa đơn giản.
Chương II. Vectơ và hệ trục tọa độ trong không gian
Bài 6. Vectơ trong không gian
- Vectơ trong không gian.
- Tổng và hiệu của hai vectơ trong không gian.
- Tích của một số với một vectơ trong không gian.
- Tích vô hướng của hai vectơ trong không gian.
II. BÀI TẬP ÔN LUYỆN A. TRẮC NGHIỆM
Chương I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Bài 1. Tính đơn điệu và cực trị của hàm số
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
Câu 1. Tìm khoảng đồng biến của hàm số: 4 2
y  x  4x  3 .
A. (0;) . B. ( ;  0) . C. ( ;   2) và (0; 2) . D. ( 2; ) . 
Câu 2. Tìm khoảng nghịch biến của hàm số: 3 2x y  . x  7
A. (;7) . B. ( ;  ) . C. ( ;
 7) và (7;).
D. (10; ) . Câu 3. Hàm số 2
y  2x  x nghịch biến trên khoảng nào. A. 0;  1 . B.   ;1  . C. 1;2 . D. 1;.
Câu 4. Hàm số nào sau đây đồng biến trên ?  A. x 1 y  . B. 3 2
y  x  4x  3x –1. x  2 C. 4 2 1 1
y  x – 2x –1 . D. 3 2 y  x  x  3x 1 . 3 2
Câu 5. Cho các hàm số sau:  x  2 I  3 2
: y  x  3x  3x 1;II  : y  sin x  2 ; x  III  3
: y   x  2; IV  : y  . 1 x
Hỏi hàm số nào nghịch biến trên toàn trục số? A. (I), (II).
B. (I), (II) và (III). C. (I), (II) và (IV). D. (II), (III).
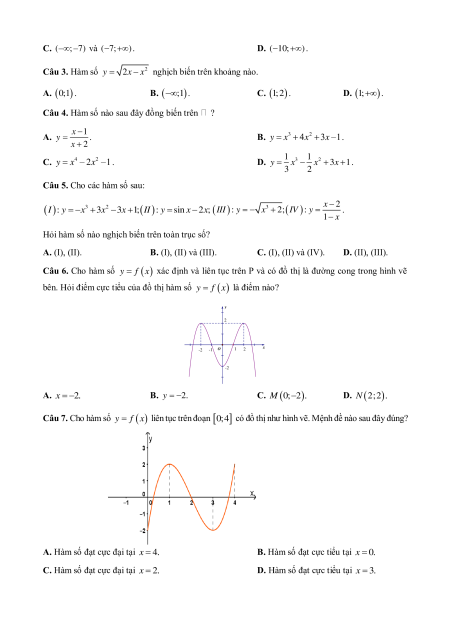
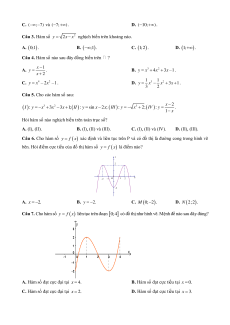
Câu 6. Cho hàm số y  f x xác định và liên tục trên  và có đồ thị là đường cong trong hình vẽ
bên. Hỏi điểm cực tiểu của đồ thị hàm số y  f x là điểm nào? y 2 x O 2 -2 -1 1 -2 A. x  2. 
B. y  2. C. M 0; 2  .
D. N 2;2.
Câu 7. Cho hàm số y  f x liên tục trên đoạn 0; 
4 có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực đại tại x  4.
B. Hàm số đạt cực tiểu tại x  0.
C. Hàm số đạt cực đại tại x  2.
D. Hàm số đạt cực tiểu tại x  3. 2   Câu 8. Gọi x 3x 3
M , n lần lượt là giá trị cực đại, giá trị cực tiểu của hàm số y  . Khi đó giá trị x  2 của biểu thức 2
M  2n bằng: A. 8. B. 7. C. 9. D. 6.
Câu 9. Hàm số nào sau đây không có cực trị? A. 2 y  2x  . B. 3 2
y  x  3x . x 1  C. 4 2 x
y  x  2x  3. D. 1 y  . x  2
Câu 10. Cho y  f x liên tục và đồng biến trên khoảng 3;1 
1 . Số nghiệm nguyên của bất phương
trình f  x f  2 11 
x  trên khoảng 3;1  1 là A. 9 . B. 8 . C. 7 . D. 10.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Câu 1. Cho hàm số y  f x có bảng xét dấu đạo hàm như sau:
a) Hàm số nghịch biến trên khoảng  ;  2  .
b) Hàm số đồng biến trên khoảng  2  ;0 .
c) Hàm số đồng biến trên khoảng  ;  0.
d) Hàm số nghịch biến trên khoảng 0;2 .  Câu 2. Cho hàm số x 3 y  . x  2
a) Hàm số nghịch biến trên \  2  .
b) Hàm số nghịch biến trên  ;  2   và  2;  .
c) Hàm số đồng biến trên .
d) Hàm số nghịch biến trên  4  ; 3   . Câu 3. Cho hàm số 4 2
y  x  2x 1. Trong các mệnh đề sau mệnh đề nào đúng? Mệnh đề nào sai?
a) Hàm số có 3 điểm cực trị.
b) Hàm số đồng biến trên các khoảng  1  ;0 và 1;.
c) Hàm số có 1 điểm cực trị.
d) Hàm số nghịch biến trên các khoảng  ;    1 và 0;  1 . Câu 4. Cho hàm số 2
y  8  2x  x . Xét tính đúng sai của các mệnh đề sau.
a) Tập xác định của hàm số là D   2  ;  4 .  b) Hàm số có 1 x y  . 2 8  2x  x
c) Hàm số nghịch biến trên khoảng 1;4 .
d) Giá trị cực đại của hàm số là 0. x  x 
Câu 5. Cho hàm số f  x 2 2 6  .  x 1
a) Hàm số f  x có tập xác định là . 2 x  x  b) Hàm số 2 8
f  x có đạo hàm f  x  .  x  2 1
c) Hàm số f  x có giá trị cực đại bằng 2.
d) Hàm số f  2
x  2 có 3 điểm cực trị.
Phần III. Trắc nghiệm trả lời ngắn
Câu 1. Cho hàm số y  f x 3 2
 x  2x  x 3 đạt cực tiểu tại x  a , cực đại tại x  b . Tính 3a 6 . b
Câu 2. Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số N t 3 2  t
 12t ,0  t 12 , trong đó N là số người bị nhiễm bệnh (đơn vị là trăm người) và t là thời gian (tuần). Gọi  ;
a b là khoảng thời gian lâu nhất mà số người bị nhiễm bệnh tăng lên. Tính 2 2
P  2a  b .
Câu 3. Trong một thí nghiệm y học, người ta cấy 1000 vi khuẩn vào môi trường dinh dưỡng bằng
thực nghiệm, người ta xác định được số lượng vi khuẩn thay đổi theo thời gian bởi công thức   100t N t  1000 
(con), trong đó t là thời gian tính bằng giây. Hỏi thời gian bằng bao nhiêu để 2 100  t
số lượng vi khuẩn đạt cực đại.
Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu chỉ chọn một phương án.
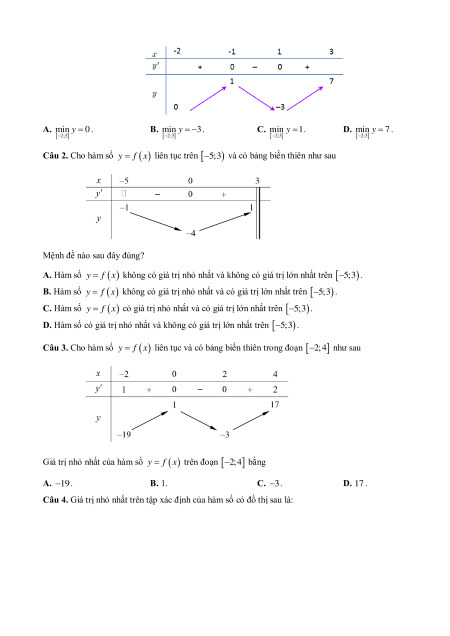
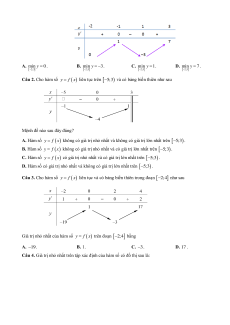
Câu 1. Giá trị nhỏ nhất của hàm số có bảng biến thiên sau trên khoảng  2  ;  3 là: