Đề thi HSG Toán 12 Sở Hải Phòng 2024 - 2025

SỞ GD&ĐT HẢI PHÒNG
KỲ THI CHỌN HSG THÀNH PHỐ CẤP THPT 2025 HSG 2024-2025 MÔN THI: TOÁN 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Đề thi gồm có ba phần: Câu trắc nghiệm nhiều phương án lựa chọn (12 Câu). Câu trắc nghiệm
đúng sai (04 Câu). Câu trắc nghiệm trả lời ngắn (6 Câu).
-------------------------------------------------------------------------------------------------------------
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án Câu 1: Cho hình chóp có đáy là hình chữ nhật, , . Tam giác
đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
là trung điểm của cạnh . Khoảng cách từ điểm đến mặt phẳng bằng A. . B. . C. . D. .
Câu 2: Tổng các nghiệm thuộc đoạn của phương trình bằng A. . B. . C. . D. . Câu 3:
Bảng dưới đây biểu diễn mẫu số liệu ghép nhóm về thời gian chạy cự li của vận
động viên trong một buổi luyện tập (đơn vị: giây)
Số trung bình của mẫu số liệu trên gần nhất với giá trị nào dưới đây? A. . B. . C. . D. .
Câu 4: Cho một cấp số cộng có và tổng số hạng đầu bằng . Tổng bằng A. . B. . C. . D. .
Câu 5: Trong mặt phẳng , cho đường tròn . Đường thẳng cắt đường tròn tại và đường thẳng cắt đường tròn tại
. Diện tích lớn nhất của tứ giác có 4 đỉnh bằng
A. . B. . C. . D. .
Câu 6: Một nhóm gồm 6 bạn nam trong đó có Hùng và 4 bạn nữ xếp hàng để chụp hình lưu niệm. Mọi
người đứng thành 2 hàng, mỗi hàng 5 người. Xác suất để Hùng đứng liền giữa hai bạn nam
đồng thời trong mỗi hàng hai bạn nữ bất kỳ không đứng cạnh nhau bằng A. . B. . C. . D. . Câu 7: Cho hàm số (với
) có đồ thị là đường cong trong hình vẽ
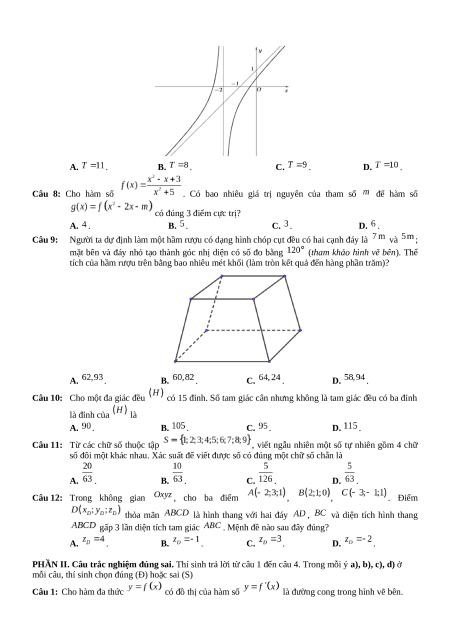
bên. Giá trị biểu thức là A. . B. . C. . D. . Câu 8: Cho hàm số
. Có bao nhiêu giá trị nguyên của tham số để hàm số
có đúng 3 điểm cực trị? A. . B. . C. . D. . Câu 9:
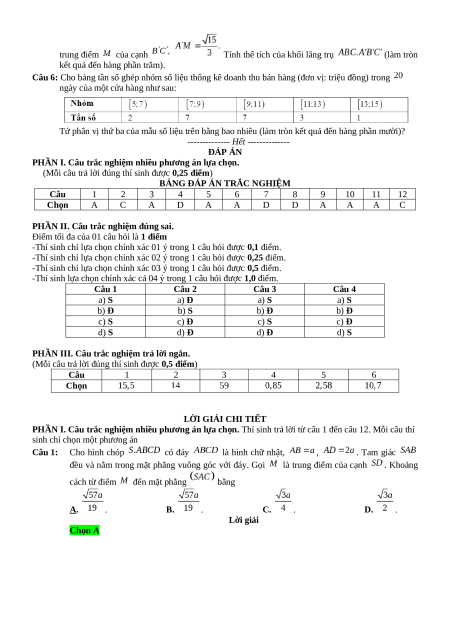
Người ta dự định làm một hầm rượu có dạng hình chóp cụt đều có hai cạnh đáy là và ;
mặt bên và đáy nhỏ tạo thành góc nhị diện có số đo bằng
(tham khảo hình vẽ bên). Thể
tích của hầm rượu trên bằng bao nhiêu mét khối (làm tròn kết quả đến hàng phần trăm)? A. . B. . C. . D. .
Câu 10: Cho một đa giác đều
có 15 đỉnh. Số tam giác cân nhưng không là tam giác đều có ba đỉnh là đỉnh của là A. . B. . C. . D. .
Câu 11: Từ các chữ số thuộc tập
, viết ngẫu nhiên một số tự nhiên gồm 4 chữ
số đôi một khác nhau. Xác suất để viết được số có đúng một chữ số chẵn là A. . B. . C. . D. .
Câu 12: Trong không gian , cho ba điểm , , . Điểm thỏa mãn
là hình thang với hai đáy , và diện tích hình thang
gấp 3 lần diện tích tam giác
. Mệnh đề nào sau đây đúng? A. . B. . C. . D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Câu 1: Cho hàm đa thức
có đồ thị của hàm số
là đường cong trong hình vẽ bên. a) Phương trình
có đúng 4 nghiệm thuộc . b) . c) Hàm số
nghịch biến trên khoảng . d) Hàm số
có đúng 2 điểm cực trị.
Câu 2: Cho hình chóp có đáy là hình thoi tâm , và . Gọi là trung điểm của . Biết
vuông góc với mặt phẳng và .
a) Gọi là số đo góc phẳng nhị diện , khi đó .
b) Góc tạo bởi đường thẳng và mặt phẳng bằng góc .
c) Thể tích khối chóp bằng . d) Gọi ,
, lần lượt là trung điểm của ba cạnh và . Khoảng cách giữa hai đường thẳng và bằng . Câu 3: Cho hàm số
a) Tập nghiệm của bất phương trình là .
b) Bất phương trình
có đúng hai nghiệm nguyên dương. c) Phương trình
có hai nghiệm phân biệt.
d) Số giá trị nguyên của thuộc đoạn để bất phương trình nghiệm đúng là 2029.
Câu 4: Một nhà máy sản xuất hai loại sản phẩm I và II từ ba nguyên liệu A, B và C. Để sản xuất sản
phẩm I nhà máy phải sử dụng nguyên liệu A và
nguyên liệu C. Để sản xuất sản
phẩm II nhà máy phải sử dụng nguyên liệu A, nguyên liệu B và nguyên liệu C.
Biết rằng nhà máy có 10 tấn nguyên liệu A, 4 tấn nguyên liệu B và 12 tấn nguyên liệu C. Giả sử
sản phẩm sản xuất ra đều được bán hết và tiền lãi khi bán mỗi tấn sản phẩm I là 3 triệu đồng, mỗi
tấn sản phẩm II là 5 triệu đồng. Gọi và lần lượt là số tấn sản phẩm I và II nhà máy cần sản xuất
a) Khi nhà máy sản xuất hai loại sản phẩm trên có lãi cao nhất thì phải sử dụng 10 tấn nguyên liệu A.
b) Nguyên liệu của nhà máy đủ để sản xuất 3 tấn sản phẩm I và tấn sản phẩm II.
c) Bất phương trình mô tả điều kiện về sử dụng nguyên liệu C của nhà máy là
d) Tiền lãi thu được khi sản xuất 2 tấn sản phẩm I và 2 tấn sản phẩm II là triệu đồng.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1: Trong rừng, có hai điểm du lịch ở vị trí
và đều cách bờ biển một khoảng bằng km (coi
đường bờ biển là một đường thẳng). Khoảng cách giữa hai vị trí
và là 18 km. Người ta dự
định đặt hai điểm nghỉ chân tại vị trí trên bờ biển sao cho và làm đường từ lần lượt qua
đến . Biết chi phí làm đường trong rừng là 1300 triệu/km và đường trên bờ
biển là 500 triệu/km. Khoảng cách giữa hai vị trí và
là bao nhiêu kilômét để tổng chi phí
làm đường nêu trên ít nhất? Câu 2: Gọi
là hai nghiệm của phương trình . Biết , trong đó
là các số nguyên dương. Tính tổng .
Câu 3: Trong không gian , cho tam giác
có là tâm đường tròn ngoại tiếp. Tính giá trị biết
Câu 4: Mạng lưới giao thông trong một thành phố được bố trí dạng lưới hình chữ nhật kích thước
như hình vẽ dưới đây. Lần đầu đến thành phố, anh Nam muốn đi từ điểm đến điểm . Biết
rằng tại các điểm giao nhau, anh Nam luôn chọn ngẫu nhiên một trong các hướng đi để quãng
đường đi từ đến là ngắn nhất. Xác suất để anh Nam không đi qua điểm giao ở vị trí là
bao nhiêu (làm tròn kết quả đến hàng phần trăm)?
Câu 5: Cho hình lăng trụ tam giác Khoảng cách từ đến là khoảng cách từ đến và lần lượt là
. Hình chiếu vuông góc của đỉnh trên mặt phẳng là