Bộ 20 đề thi HSG Toán 12 có lời giải

SỞ GD&ĐT THANH HÓA
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH NĂM HỌC 2024 - 2025 2024-2025 MÔN THI: TOÁN 12
Thời gian: 90 phút (Không kể thời gian phát đề)
Đề thi gồm có ba phần: Câu trắc nghiệm nhiều phương án lựa chọn (20 Câu). Câu trắc nghiệm
đúng sai (06 Câu). Câu trắc nghiệm trả lời ngắn (06 Câu).
-------------------------------------------------------------------------------------------------------------
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí
sinh chỉ chọn một phương án. 2
Câu 1. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số x  x  9 y  bằng: x 1 A. 4 5 . B. 6 5 . C. 3 2 . D. 2 2 .
Câu 2. Gieo đồng thời hai con xúc xắc I và II cân đối, đồng chất một lần. Ta gọi biến cố A: “Có ít nhất
một con xúc xắc xuất hiện mặt 6 chấm”. Khi đó xác suất P  A của biến cố A là:
A. P A 11  .
B. P A 1  .
C. P A 25  .
D. P A 15  . 36 36 36 36
Câu 3. Nghiệm của phương trình 2cos  x    2    0 là  4  x  k x  k2 A.   k ¢  . B.   k ¢  .
x    k2
x    k2  2  2 x  k 2  x  k C.   k ¢ . D.   k  ¢  .
x    k
 x    k  2  2 Câu 4. Biết    
 với a,b  . Tính giá trị a  8b .   2 lim
4x 3x 1 ax b 0 x A. 4 . B. 2 . C. 5. D. 1  . Câu 5.  
Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số sin x 2cosx 1 y 
lần lượt là M,m . Khi
sin x  cos x  2
đó 2M  m bằng. A. 1. B. 2 . C. 1  . D. 0 .
Câu 6. Bạn Chi rất thích nhảy hiện đại. Thời gian tập nhảy mỗi ngày trong thời gian gần đây của bạn
Chi được thống kê lại ở bảng sau: Thời gian (phút) 20 25  ;  25 30  ;  30 35  ;  35 40  ;  40 45  ;  Số ngày 6 7 5 6 4
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là A. 165 . B. 27 5 . . C. 12.2. D. 155 . 14 13
Câu 7. Trong không gian với hệ trục tọa độ Oxyz , cho hình hộp ABC .
D A'B'C'D' có các đỉnh
A'1; 2;3,C' 1; 4;5,B 3;3; 2 ,D 5;3; 2  . Tìm tọa độ D' .
A. D'4;3; 2 .
B. D'4;3;6 . C. D'2;4;  1 .
D. D'0;2;  1 .
Câu 8. Trong không gian Oxyz , cho A1; 2  ;3,B 0;2; 1  ,C  2
 ;0;1  . Xác định tọa độ vectơ r uuur uuur
u  2AB  AC . r r r r
A. u  1;6;6 .
B. u  1;6;2 .
C. u  7;2; 2   .
D. u  4;14; 1  4 .
am  nb
Câu 9. Đặt a  log 3, b  log 3. Nếu biểu diễn log 45 
(với m,n, p  ) thì 2 5 6
ba  p
13m 12n  2024 p bằng bao nhiêu? A. 3012 . B. 2028 . C. 2061. D. 1024.
Câu 10. Khảo sát thu nhập theo tháng của người lao động ở một công ty thu được số ghép nhóm sau:
Tính mức thu nhập trung bình của người lao động ở công ty trên (đơn vị: triệu đồng) A. 10,5 . B. 12,5 . C. 11,75. D. 11.
Câu 11. Cho hàm số y  f x xác định trên , hình bên là đồ thị của
hàm số y  f  x . Hỏi hàm số y  f x nghịch biến trên khoảng nào dưới đây? A. 1;3. B. 0;  1 và 2; . C. 0;. D. ;2 .    
Câu 12. Trong không gian cho hai vectơ a và b tạo với nhau góc o
120 và a  3, b  5 . Tính độ dài  
của vectơ a b. A. 19. B. 7 . C. 49 . D. 19 .
Câu 13. Một cấp số cộng u có tổng của n số hạng đầu   , n 
S được tính theo công thức 2 S n n n 3 5 n *
n . Tìm số hạng đầu u và công sai d của cấp số cộng đó. 1 A. u  8  ;d  6 .
B. u  6;d  8 .
C. u  8;d  6.
D. u  8;d  6 . 1 1 1 1    
Câu 14. Cho lăng trụ tam giác ABC.A B  C
  . Đặt AA  a, AB  b, AC  c. Gọi I là điểm thuộc đoạn
CC thỏa mãn IC  3IC , G là trọng tâm tứ diện BA B  C
 . Khẳng định nào sau đây là đúng?     A. 1
IG  a  b  2c . B. 1  3 1
IG   a  b  c . 4 2 4 4    C. 1  3
IG  a  c . D. 1 3
IG  b  c . 4 4 2 4
Câu 15. Cho tứ diện ABCD . Trên mỗi cạnh của tứ diện, ta đánh dấu 4 điểm chia đều các cạnh đó thành
các phần bằng nhau. Hỏi có thể lập được bao nhiêu tam giác mà ba đỉnh lấy từ 24 điểm đánh
dấu sao cho mặt phẳng chứa tam giác đó song song với đúng một cạnh của tứ diện đã cho. A. 432 . B. 288 . C. 336. D. 216 .
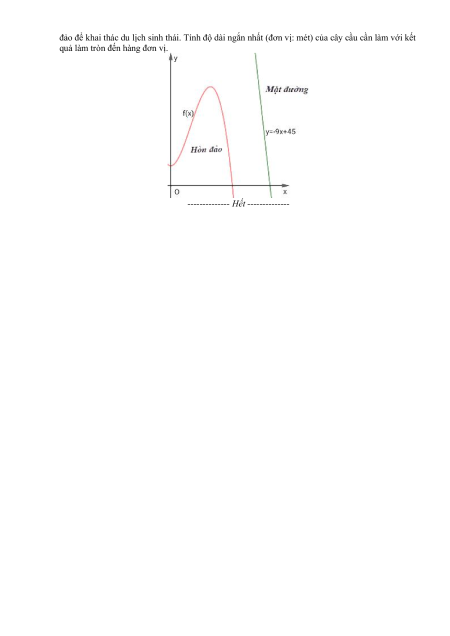
Câu 16. Người ta dựng trên mặt đất bằng phẳng một chiếc lều từ một tấm bạt hình chữ nhật có chiều dài
6 m và chiều rộng 5m bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh chiều
dài của tấm bạt sao cho hai mép cạnh chiều rộng của tấm bạt sát đất và cách nhau x (m) , hai
đầu hồi của lều được thiết kế cửa ra, vào và có thể khép kín (tham khảo hình vẽ dưới. Thể tích
không gian phía trong lều lớn nhất bằng a 3 (m ) với *
a,b  và phân số a tối giản. Tính giá b b trị a  b . A. 35. B. 27 . C. 47 . D. 28 .
Câu 17. Cho hàm số y 2024
 f (x) có bảng biến thiên như hình vẽ. Đồ thị hàm số y  g x  có f x 1
tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. 8. B. 6. C. 5. D. 4.
Câu 18. Trong Không gian Oxyz cho các điểm ( A 5; 3  ;2), B 2;1; 2
 . Gọi M, N là hai điểm phân biệt
thay đổi thỏa mãn BM  BN  2 và ,
A M , N thẳng hàng. Giá trị nhỏ nhất của biểu thức
S  2.AM  5.AN có dạng 7 m  n với ,
m n là các số tự nhiên. Tính giá trị 5m  . n A. 215 B. 211. C. 261 . D. 169 .
Câu 19. Cho a,b là các số thực thỏa mãn 4
1 a  b  a . Tìm giá trị nhỏ nhất của biểu thức 3 2    log a  a P      a 3log  . a   b   b  A. 4 . B. 1  8. C. 2  6. D. 6 .
Câu 20. Cho tứ diện OABC có AOB  BOC  60 ; AOC  90 ; OA  OB  OC  1. M là điểm thuộc 
cạnh OA sao cho AM  2.MO ; N là trung điểm của BC . Tính độ dài véc tơ MN . A. 4 . B. 2 . C. 3 . D. 5 . 5 3 4 6
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở
mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S). 2 Câu 1. Cho hàm số x  x  6 y 
có đồ thị là đường cong C. Giả sử ,
A B là hai điểm thuộc 2 nhánh x 1
của đồ thị C sao cho AB song song với trục hoành. Xét tính đúng sai của các mệnh đề sau:
a) Trên đồ thị Ccủa hàm số có 8 điểm mà hoành độ và tung độ đều là số nguyên.
b) Có 2 tiếp tuyến của đồ thị C song song với đường thẳng d : y  7x 18.
c) Giá trị nhỏ nhất của đoạn thẳng AB bằng 2 5 .
d) Đường tròn T  x  2   y  2 2 : 1
1  R cắt C tại 4 điểm phân biệt khi và chỉ khi 2 R 12 2  1 .
Câu 2. Cho hình lập phương ABCD.AB C  D
  có cạnh bằng 6 và O là giao điểm của AC và BD. Trong
các mặt phẳng chứa các đường thẳng CD , gọi () là mặt phẳng tạo với mặt phẳng BDD B  
một góc nhỏ nhất; đường thẳng   () (BDD B
 ) ; điểm E   BD. Kẻ OH   tại H . Xét
tính đúng sai các mệnh đề sau:
a) Góc giữa () và (BDD'B') là góc OHC . b) DE  6 2 .
c) Thể tích tứ diện C 'BCE là V  72 .
d) Khoảng cách từ A đến mặt phẳng () bằng 2 6 .
Câu 3. Một hộp chứa 45 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 45. Lấy ngẫu
nhiên 3 quả cầu từ hộp đó. Xét tính đúng sai của các mệnh đề sau:
a) Số cách lấy được cả 3 quả cầu đánh số chẵn bằng 1540.
b) Xác suất để tổng 3 số ghi trên 3 quả cầu là số lẻ bằng 1 . 2
c) Xác suất để tổng 3 số ghi trên 3 quả cầu là số chia hết cho 4 bằng 323 . 1290
d) Xác suất để tích 3 số ghi trên 3 quả cầu là một số chia hết cho 8 bằng 523 . 1290
Câu 4. Tại một trường THPT, để khảo sát năng lực học môn Toán của hai lớp 12E và 12F, giáo viên đã
cho học sinh ở hai lớp làm bài kiểm tra khảo sát đầu năm, thống kê điểm của học sinh được cho trong bảng sau:
Xét tính đúng sai của các mệnh đề sau:
a) Dựa vào điểm trung bình môn Toán ta đánh giá được lớp 12E học tốt môn Toán hơn lớp 12F.
b) Khoảng tứ phân vị của mẫu số liệu thống kê điểm của lớp 12F nhỏ hơn 2,9 .
c) Điểm thi có số học sinh đạt được nhiều nhất ở lớp 12E nhỏ hơn ở lớp 12F.
d) Dựa vào độ lệch chuẩn của mẫu số liệu thống kê ghép nhóm, ta thấy rằng lớp 12E học đều hơn lớp 12F.
Câu 5. Huyết áp là áp lực cần thiết tác động lên thành của động mạch để đưa máu từ tim đến nuôi dưỡng
cơ thể. Huyết áp được tạo ra do lực co bóp của tim và sức cản của thành động mạch. Mỗi lần tim
đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu gọi là
huyết áp tâm thu và huyết áp tâm trương. Chỉ số huyết áp của chúng ta được viết là tâm thu/tâm
trương. Chỉ số huyết áp 120/80 là bình thường. Giả sử huyết áp của một người nào đó được mô
hình hóa bởi hàm số P(t)= 115+ 20sin(180 t
p ) ở đó P(t) là huyết áp tính theo đơn vị mmHg
(milimét thủy ngân) và thời gian t tính theo phút.
Xét tính đúng sai của các mệnh đề sau:
a) Số lần huyết áp tâm thu xảy ra trong khoảng thời gian một giờ đồng hồ là 5000 .
b) Chỉ số huyết áp là 135 / 95 .
c) Chu kì của hàm P(t) là 90.
d) Trong một phút, số lần mà tốc độ thay đổi huyết áp bằng 1800p ( mmHg /phút) là 180 .
Câu 6. Trong không gian Oxyz , cho tam giác ABC có ( A 2; 1  ;2), B(4;3; 2  ), C(5; 1  ;6) . Xét tính đúng
sai của các mệnh đề sau:
a) Chu vi tam giác ABC là 20.