ĐỀ SỐ 49
Câu 1:( 3đ) Thực hiện phép tính. 1 3 2 128 75 1 162 2 48 a. 2 5 3
c. ( 2 10)( 3 5 ) 1 1 b. 3 2 3 2 1 1 x 1 M :
Câu 2:( 2đ) Cho biểu thức:
x 1 x x x 2 x 1
a. Tìm x để biểu thức M có nghĩa. b. Rút gọn biểu thức M.
c. So sánh giá trị của M với 1. Câu 3:(1,5đ)
Cho hàm số y = -x + 2
(d) và y = mx + 2 (d’)
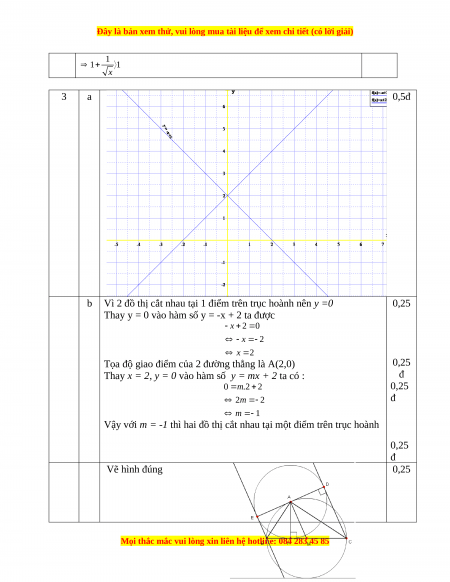
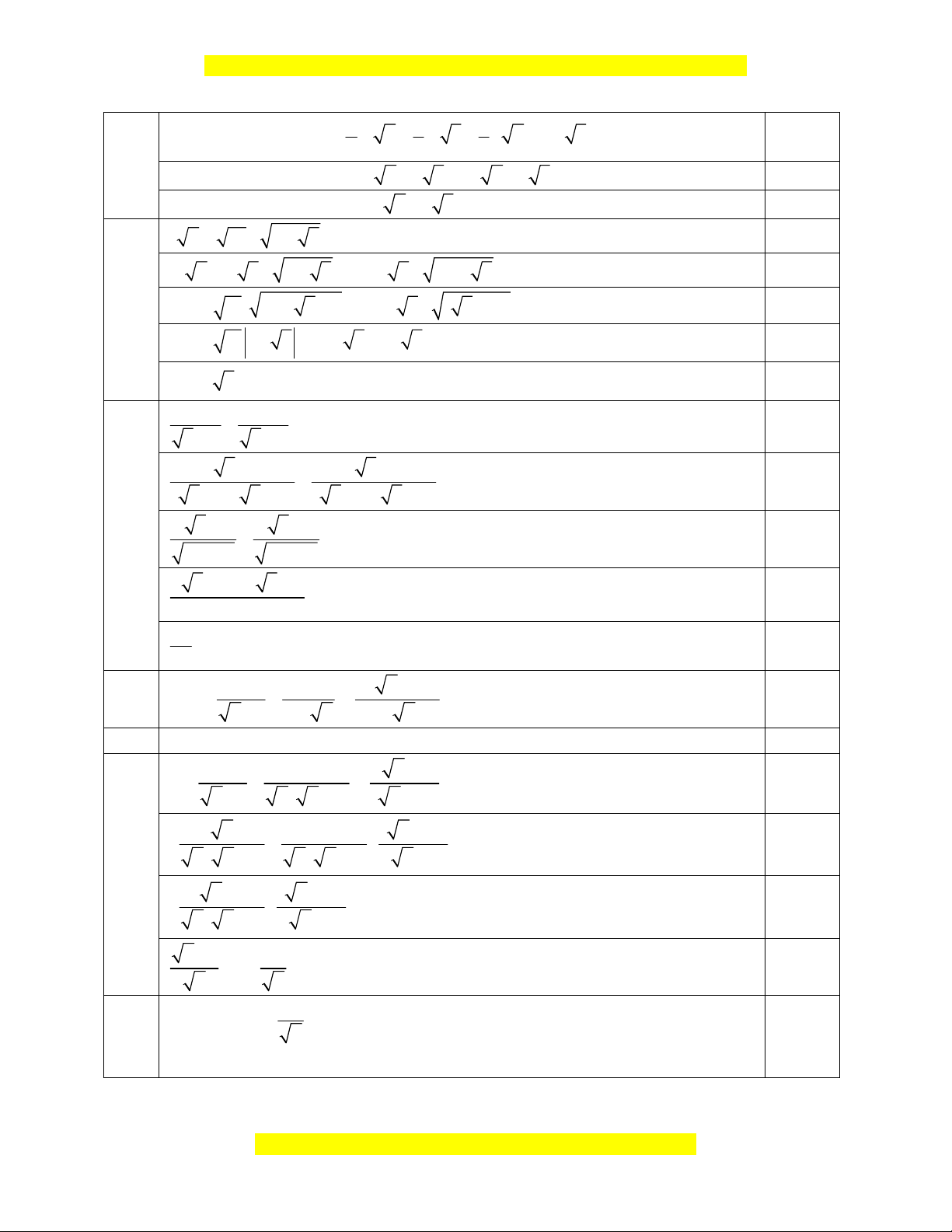
a. Với m = 1 vẽ đồ thị 2 hàm số trên cùng một hệ trục tọa độ.
b. Tìm m để ( d) và (d’) cắt nhau tại 1 điểm trên trục tung.
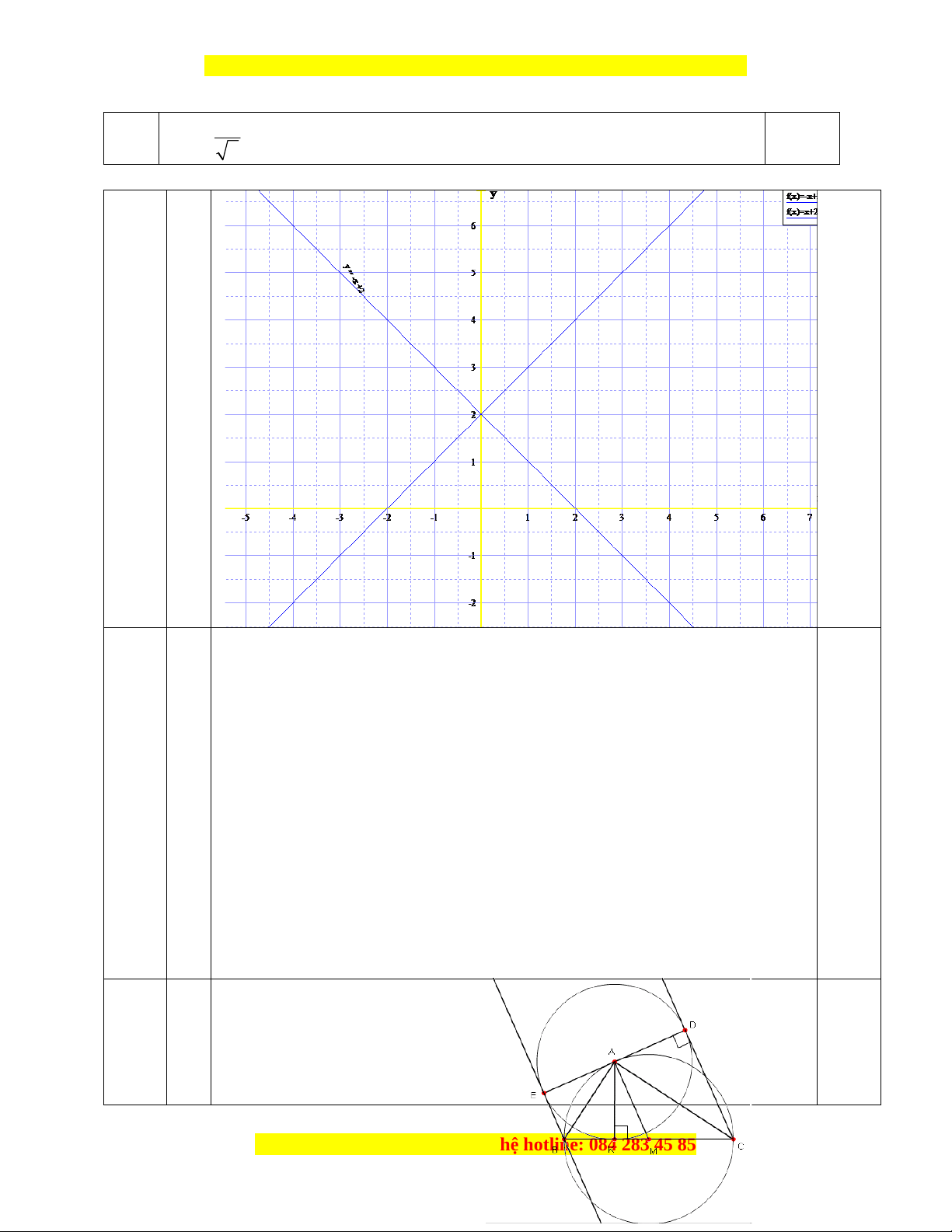
Câu 5:( 3,5đ) Cho tam giác ABC đường cao AH. Vẽ đường tròn tâm A bán kính
AH, kẻ các tiếp tuyến BE, CD với đường tròn ( E, D là các tiếp điểm khác H).
a) Tính AH, SinB, tgC biết AB = 6cm, BC = 10cm
b) Chứng minh rằng BC = BE + CD
c) Chứng minh 3 điểm D, A, E thẳng hàng .
d) DE tiếp xúc với đường tròn đường kính BC
Chú ý : độ dài các cạnh chỉ áp dụng để tính câu a
--------------Hết--------------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm. ĐÁP ÁN ĐỀ SỐ 49 Câ Đáp án Điểm u 1 3 2 128 75 1 162 2 48 a) 2 5 3
1 3 8 0.5
.8 2 .5 3 9 2 2.4 3 1a 2 5 3 4 2 3 3 24 2 8 3 0.25 2 8 2 5 3 0.25 ( 2 10)( 3 5 ) 0,25 2(1 5)( 3 5 ) ( 1 5)( 6 2 5 ) 1b 2 ( 0,25 1 5)( 1 2 5 5) ( 1 5)( ( 5 1) ( 1 5) 1 5 ( 1 5)(1 5) 0,25 2 0,25 = 2 1 5 1 5 4 2 2 5 2 5 2 2( 5 2) 2( 5 2) 0,25
( 5 2)( 5 2) ( 5 2)( 5 2) 2 5 4 2 5 4 0,25 1c 2 2 2 2 5 2 5 2 2 5 4 2 5 4 0,25 5 4 8 0,25 8 1 2 1 1 x 1 M : x 1 x x
x 2 x 1 2a
a) Đkxđ: x >0 và x 1 0,5 1 1 x 1 0,25 : 2 x 1 x( x 1) ( x 1) 2 x 1 ( x 1) 0,25 2b x( x 1) x( x 1) x 1 2
x 1 ( x 1) 0,25 x( x 1) x 1 x 1 1 0,25 1 x x 1 0,25 0
Vì x >0 nên x 2c
1 1 1 x 3 a 0,5đ b
Vì 2 đồ thị cắt nhau tại 1 điểm trên trục hoành nên y =0 0,25
Thay y = 0 vào hàm số y = -x + 2 ta được x 2 0 x 2 x 2
Tọa độ giao điểm của 2 đường thẳng là A(2,0) 0,25
Thay x = 2, y = 0 vào hàm số y = mx + 2 ta có : đ 0 . m 2 2 0,25 2m 2 đ m 1
Vậy với m = -1 thì hai đồ thị cắt nhau tại một điểm trên trục hoành 0,25 đ Vẽ hình đúng 0,25
a
Áp dụng định lý Pitago cho tam giác ABC vuông tại A ta có: 2 2 2
AB AC BC 2 2 2
AC BC AB 2 AC 1 00 36 0,25 AC 8 cm
Mµ AH BC (gt) AB. AC = BC. AH A . B AC 6.8 AH 4 ,8 0,25 BC 10 AC 8 4 Sin B BC 10 5 0,25 0 B 5 3 AB 6 3 tgC AC 8 4 0,25 b Chứng minh được:
BC là tiếp tuyến của (A; AK) BE BK 0,25 Ta có : CD C K 0,25 BC = BE + CD c
Theo tính chất của 2 tiếp tuyến cắt nhau . 1
A A DAK 1 2 0,25 2 A A 2 .A DAK 1 2 2 1
A A KAE 0,25 ta có: 3 4 2 A A 2 .A KAE 3 4 3 Ta có: DAE =
DAK KAE DAE = A A A A 2 2 3 4 0,25 2. A A 2 3 d DAE = = 2. 900= 1800 0,25
Vậy 3 điểm A, D, E thẳng hàng
Gọi M là trung điểm của BC 0,25
Chứng minh được MA là đường trung bình của hình thang BCDE 0,25
Đề thi Toán 9 học kì 1 năm 2022 - 2023 - Đề 49
578
289 lượt tải
MUA NGAY ĐỂ XEM TOÀN BỘ TÀI LIỆU
CÁCH MUA:
- B1: Gửi phí vào TK:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official ( nhấn vào đây ) để xác nhận thanh toán và tải tài liệu - giáo án
Liên hệ ngay Hotline hỗ trợ: 084 283 45 85
Đề thi được cập nhật liên tục trong gói này từ nay đến hết tháng 6/2023. Chúng tôi đảm bảo đủ số lượng đề đã cam kết hoặc có thể nhiều hơn, tất cả có BẢN WORD, LỜI GIẢI CHI TIẾT và tải về dễ dàng.
Để tải tài liệu gốc về máy bạn click vào nút Tải Xuống ở trên!
Thuộc bộ (mua theo bộ để tiết kiệm hơn):
- Tailieugiaovien.com.vn giới thiệu bộ 60 đề thi Toán 9 Học kì 1 có lời giải chi tiết, mới nhất năm 2022 - 2023 nhằm giúp Giáo viên có thêm tài liệu tham khảo ra đề thi Toán lớp 9.
- File word có lời giải chi tiết 100%.
- Mua trọn bộ sẽ tiết kiệm hơn tải lẻ 50%.
Đánh giá
4.6 / 5(578 )5
4
3
2
1
Trọng Bình
Tài liệu hay
Giúp ích cho tôi rất nhiều
Duy Trần
Tài liệu chuẩn
Rất thích tài liệu bên VJ soạn (bám sát chương trình dạy)
TÀI LIỆU BỘ BÁN CHẠY MÔN Toán Học
Xem thêmTÀI LIỆU BỘ BÁN CHẠY Lớp 9
Xem thêmTài liệu bộ mới nhất

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
ĐỀ SỐ 49
Câu 1:( 3đ) Thực hiện phép tính.
a.
1 3 2
128 75 1 162 2 48
2 5 3
c.
( 2 10)( 3 5 )
b.
1 1
3 2 3 2
Câu 2:( 2đ) Cho biểu thức:
1 1 1
:
1 2 1
x
M
x x x x x
a. Tìm x để biểu thức M có nghĩa.
b. Rút gọn biểu thức M.
c. So sánh giá trị của M với 1.
Câu 3:(1,5đ)
Cho hàm số y = -x + 2 (d) và y = mx + 2 (d’)
a. Với m = 1 vẽ đồ thị 2 hàm số trên cùng một hệ trục tọa độ.
b. Tìm m để ( d) và (d’) cắt nhau tại 1 điểm trên trục tung.
Câu 5:( 3,5đ) Cho tam giác ABC đường cao AH. Vẽ đường tròn tâm A bán kính
AH, kẻ các tiếp tuyến BE, CD với đường tròn ( E, D là các tiếp điểm khác H).
a) Tính AH, SinB, tgC biết AB = 6cm, BC = 10cm
b) Chứng minh rằng BC = BE + CD
c) Chứng minh 3 điểm D, A, E thẳng hàng .
d) DE tiếp xúc với đường tròn đường kính BC
Chú ý : độ dài các cạnh chỉ áp dụng để tính câu a
--------------Hết--------------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
ĐÁP ÁN ĐỀ SỐ 49
Câ
u
Đáp án Điểm
a)
1 3 2
128 75 1 162 2 48
2 5 3
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
1a
1 3 8
.8 2 .5 3 9 2 2.4 3
2 5 3
0.5
4 2 3 3 24 2 8 3
0.25
28 2 5 3
0.25
1b
( 2 10)( 3 5 )
2(1 5)( 3 5 ) (1 5)( 6 2 5 )
0,25
2
(1 5)( 1 2 5 5) (1 5)( ( 5 1)
0,25
(1 5) 1 5 (1 5)(1 5)
0,25
=
2
2
1 5 1 5 4
0,25
1c
2 2
5 2 5 2
2( 5 2) 2( 5 2)
( 5 2)( 5 2) ( 5 2)( 5 2)
0,25
2 2 2 2
2 5 4 2 5 4
5 2 5 2
0,25
2 5 4 2 5 4
5 4
0,25
8
8
1
0,25
2
1 1 1
:
1 2 1
x
M
x x x x x
2a a) Đkxđ: x >0 và x
1
0,5
2b
2
1 1 1
:
1 ( 1) ( 1)
x
x x x x
0,25
2
1 ( 1)
( 1) ( 1) 1
x x
x x x x x
0,25
2
1 ( 1)
( 1) 1
x x
x x x
0,25
1 1
1
x
x x
0,25
2c
Vì
x
>0 nên
1
0
x
0,25
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
1
1 1
x
3 a 0,5đ
b Vì 2 đồ thị cắt nhau tại 1 điểm trên trục hoành nên y =0
Thay y = 0 vào hàm số y = -x + 2 ta được
2 0
2
2
x
x
x
Tọa độ giao điểm của 2 đường thẳng là A(2,0)
Thay x = 2, y = 0 vào hàm số y = mx + 2 ta cóZ:
0 .2 2
2 2
1
m
m
m
Vậy với m = -1 thì hai đồ thị cắt nhau tại một điểm trên trục hoành
0,25
0,25
đ
0,25
đ
0,25
đ
Vẽ hình đúng 0,25
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85

Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
a Áp dụng định lý Pitago cho tam giác ABC vuông tại A ta có:
2 2 2
2 2 2
2
100 36
8
AB AC BC
AC BC AB
AC
AC cm
Mµ AH
BC (gt)
AB. AC = BC. AH
. 6.8
4,8
10
AB AC
AH
BC
8 4
Sin
10 5
AC
B
BC
0
53B
6 3
8 4
AB
tgC
AC
0,25
0,25
0,25
0,25
b
c
d
Chứng minh được:
BC là tiếp tuyến của (A; AK)
Ta có :
BE BK
CD CK
BC = BE + CD
Theo tính chất của 2 tiếp tuyến cắt nhau .
ta có:
1 2
3 4
1
2
1
2
A A DAK
A A KAE
1 2 2
3 4 3
2.
2.
A A A DAK
A A A KAE
Ta có:
DAE
=
DAK KAE
DAE
=
2 2 3 4
A A A A
DAE
=
2 3
2. A A
= 2. 90
0
= 180
0
Vậy 3 điểm A, D, E thẳng hàng
Gọi M là trung điểm của BC
Chứng minh được MA là đường trung bình của hình thang BCDE
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85
Đây là bản xem thử, vui lòng mua tài liệu để xem chi tiết (có lời giải)
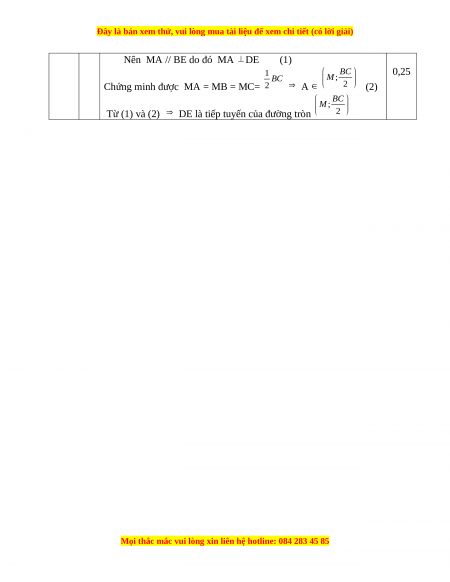
Nên MA // BE do đó MA
DE (1)
Chứng minh được MA = MB = MC=
1
2
BC
A
;
2
BC
M
(2)
Từ (1) và (2)
DE là tiếp tuyến của đường tròn
;
2
BC
M
0,25
Mọi thắc mắc vui lòng xin liên hệ hotline: 084 283 45 85